具有恐惧效应和Allee效应的合作捕食系统的稳定性分析

叶鹏辉

（安庆师范大学数理学院，安徽安庆 246133）

捕食者-食饵模型一直是生物数学研究的重要问题。近几年关于捕食者对食饵产生的恐惧效应吸引了众多学者的关注，有学者研究了一系列关于功能反应函数的恐惧效应[1-2]，也有学者研究了在一般的线性功能反应下捕食者不仅会对食饵产生恐惧效应，还会由捕食者的捕食行为对食饵产生Allee效应。研究表明，除了捕食者的直接捕食行为会对食饵造成伤害，捕食行为对食饵产生的恐惧效应还可以使食饵的增长速度降低40%，那么在繁殖过程中食饵就会由于觅偶困难而引起强Allee效应[3]。近年来有学者对合作捕获和恐惧效应也进行了研究[4-5]，受此启发，本文建立了一类捕食者合作捕获对食饵产生恐惧效应和强Allee效应的模型，具体如下：

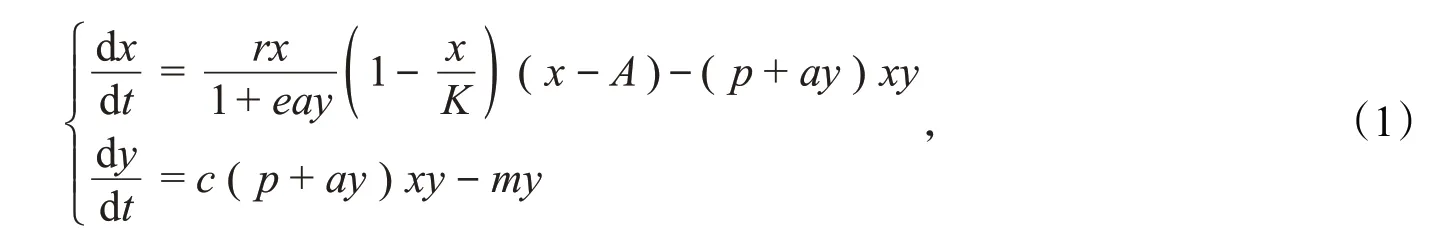
其中，x表示食饵的密度，y表示捕食者的密度，r是食饵的内禀增长率，e是食饵对捕食者产生的恐惧因子，a表示合作强度参数，K是环境的容纳量，A是食饵产生的强Allee效应阈值，p是捕食者对食饵的攻击率，c是捕食者的能量转化率，m是捕食者的自然死亡率，所有参数皆为正值。为了简化计算，对系统（1）进行无量纲化，令

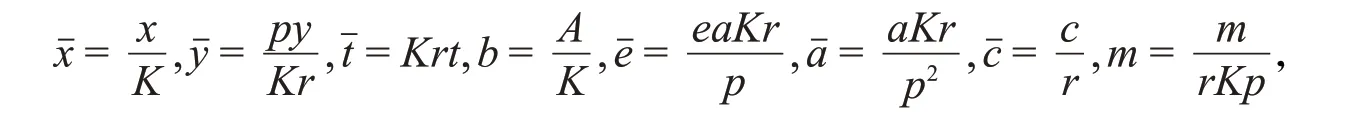
去掉变量上的横杠，得到如下模型：

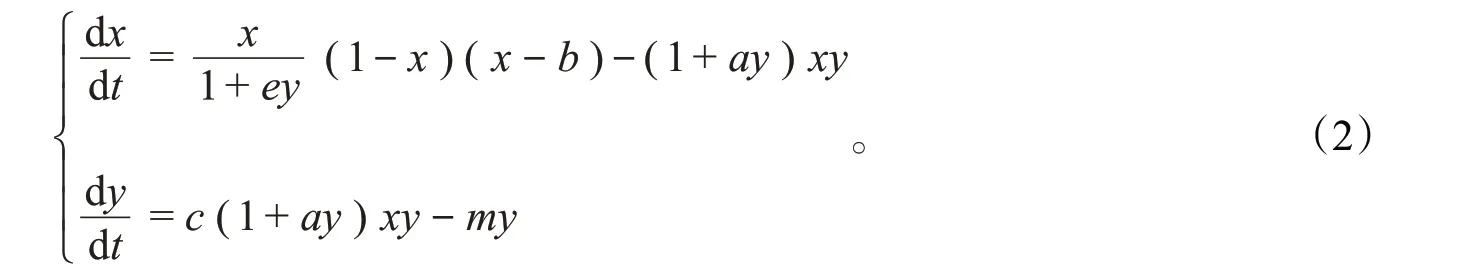
这里由于Allee效应的参数A小于环境容纳量K，所以无量纲化后0 ＜b＜1。接下来，讨论系统（2）的各类平衡点的存在性和稳定性，并通过数值模拟验证结论的可行性。

1 模型分析

1.1 平衡点的存在性

考虑代数方程组

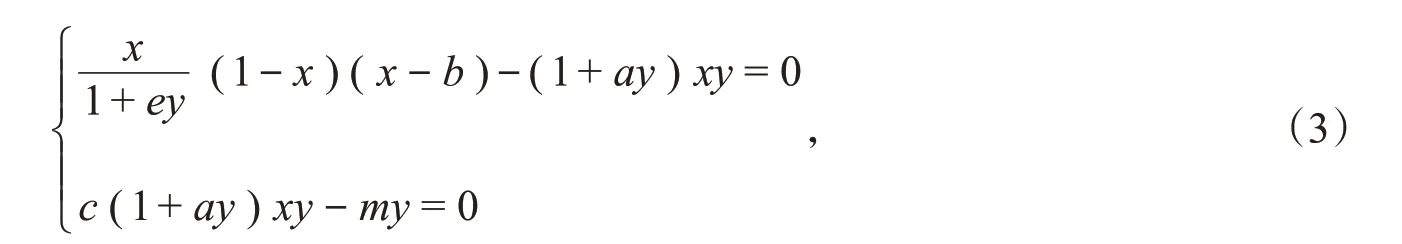
系统（2）的平衡点为代数方程组（3）的非负解，系统（2）有边界平衡点E0=(0,0)，E1=(b,0)和E2=(1,0)，其中E0表示灭绝平衡点，E1和E2表示没有捕食者的边界平衡点。接下来考虑内部平衡点的存在条件。

定理1当cb＜m＜c时，系统（2）存在唯一的内部平衡点。

证明现在考虑系统（2）的内部平衡点，先将式（3）化简为

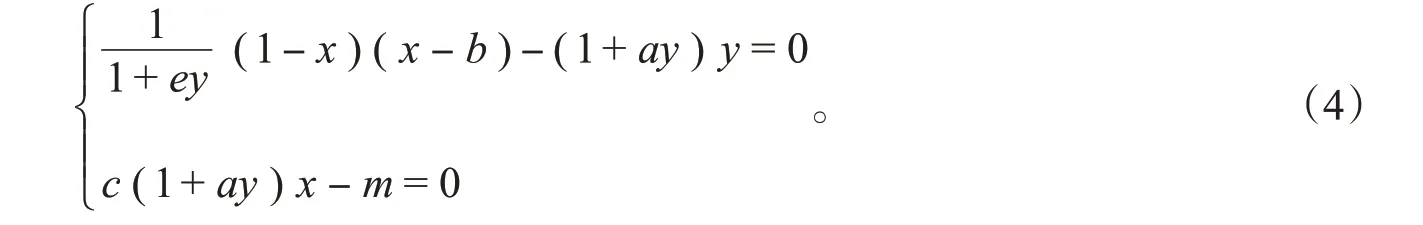
记E*=(x*,y*)是系统（2）的内部平衡点，那么有

由于ρ0、ρ1、ρ2、ρ3都是正值，而ρ4、ρ5的正负性不确定，因此考虑以下三个区域：

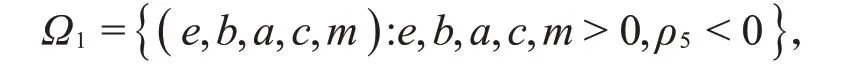
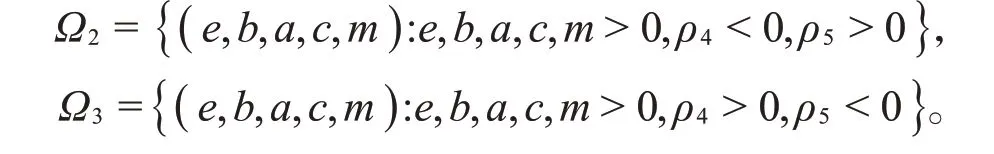
当式（5）所有的参数都在Ω1中，则有

即cb＜m＜c。因此，由笛卡尔定理[6]可知，当cb＜m＜c时，式（5）只有唯一的正解，那么系统（2）只存在唯一的内部平衡点。

定理2当系统（2）的参数满足下列任意一个条件：

（1）当a(1-b)＞1时，m＞c或m＜cb，

（2）当a(1-b)＜1时，m＞或m＜cb，

那么系统（2）存在两个内部平衡点。

证明当m＞时，有ρ4＜0；而当m＞c或m＜cb时，有ρ5＞0。下面讨论与cb，b之间的关系。

（Ⅰ）当ab(b-1)＞1时，即，而0 ＜b＜1，所以不存在的情况。

（Ⅱ）当a(1-b)＞1时，即，这时系统（2）的参数a和b满足a(1-b)＞1，参数m则需要满足m＞c或m＜cb。那么当系统（2）的参数满足a(1-b)＞1，m＞c或m＜cb时，有ρ4＜0，ρ5＞0。

（Ⅲ）当a(1-b)＜1时，即，这时系统（2）的参数a和b满足a(1-b)＜1，参数m则需要满足或m＜cb。那么当系统（2）的参数满足a(1-b)＜1，或m＜cb时，有ρ4＜0，ρ5＞0。

由笛卡尔定理[6]可知，当系统（2）的所有参数都在Ω2时，式（5）存在两个正解，那么系统（2）存在两个内部平衡点。

定理3当系统（2）的参数满足下列任意一个条件：

（1）当a(1-b)＞1时，cb＜m＜，

（2）当a(1-b)＜1时，cb＜m＜c，

那么系统（2）不存在内部平衡点。

证明当时，有ρ4＞0；当cb＜m＜c时，有ρ5＜0。由定理2 的证明可知不存在的情况，所以这里需要分两种情况讨论：

（Ⅰ）当a(1-b)＞1 且ab(b-1)＜1 时，即，由于0 ＜b＜1，那么参数a、b只考虑满足a(1-b)＞1的情况，当系统（2）的参数满足a(1-b)＞1，cb＜m＜时，有ρ4＞0，ρ5＜0。

（Ⅱ）当a(1-b)＜1时，即，这时系统（2）的参数a、b满足a(1-b)＜1，当系统（2）的参数满足a(1-b)＜1，cb＜m＜c时，有ρ4＞0，ρ5＜0。

由笛卡尔定理[6]可知，当系统（2）的参数都在Ω3时，式（5）不存在正解，系统（2）不存在内部平衡点。

1.2 平衡点的稳定性分析

定理4边界平衡点E0是稳定的结点；当c＜m，E1是鞍点，E2是稳定的结点；当cb＜m＜c，E1，E2都是鞍点；当cb＞m，E1是不稳定的结点，E2是鞍点。

证明E0、E1和E2的雅可比矩阵分别为

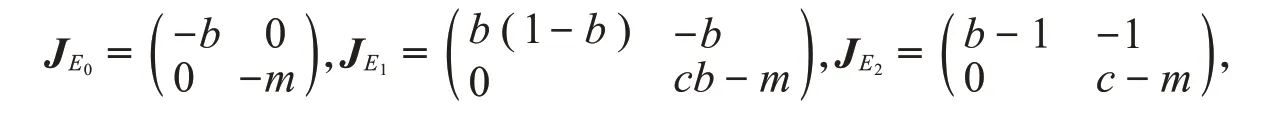
可以得出E0是稳定的结点，由参数无量纲化可知0 ＜b＜1，所以b(1-b)＞0，b-1＜0。当c＜m时，cb-m＜0，c-m＜0，此时E1是鞍点，而E2是稳定的结点。当cb＜m＜c时，E1、E2都是鞍点。当cb＞m时，E1是不稳定的结点，而E2是鞍点。

定理5当内部平衡点E*满足Tr(JE*)＜0 且det(JE*)＞0 时，E*稳定；当内部平衡点E*满足det(JE*)＜0时，E*不稳定；当内部平衡点E*满足Tr(JE*)＞0且det(JE*)＞0时，E*不稳定。

证明内部平衡点E*(x*,y*)的雅可比矩阵是

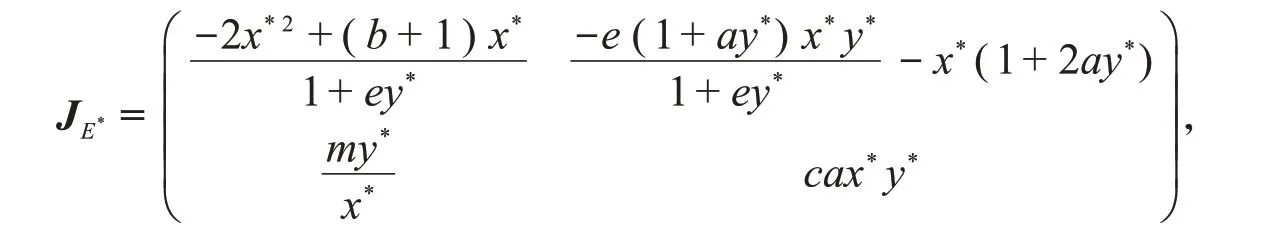
并且对应的特征方程是λ2-Tr(JE*)λ+det(JE*)=0，其中，

内部平衡点的稳定性取决于Tr(JE*)和det(JE*)的正负性，由Routh-Hurwitz 判据可知，当Tr(JE*)＜0且det(JE*)＞0时，内部平衡点E*稳定；而当det(JE*)＜0，或者Tr(JE*)＞0且det(JE*)＞0时，内部平衡点E*不稳定。

2 数值模拟

利用Matlab数值模拟来验证边界平衡点的稳定性、内部平衡点的存在性及稳定性。

2.1 边界平衡点的稳定性

在定理4 的条件c＜m下，选取一组参数a=2，b=0.5，e=2，c=1，m=1.5，边界平衡点E0=(0,0)，E1=(0.5,0)和E2=(1,0)如图1中星号点所在位置，其对应的相图轨线如图1所示。由图1可知，E0和E2是稳定的结点，E1是鞍点。

图1 边界平衡点的稳定性

在定理4 的条件cb＜m＜c下，选取一组参数a=1，b=0.2，e=1，c=1，m=0.3，则边界平衡点E0(0,0)，E1(0.2,0)和E2(1,0)如图2中星号点所在位置，其对应的相图轨线如图2所示。由图2可知，E0是稳定的结点，E1和E2是鞍点。

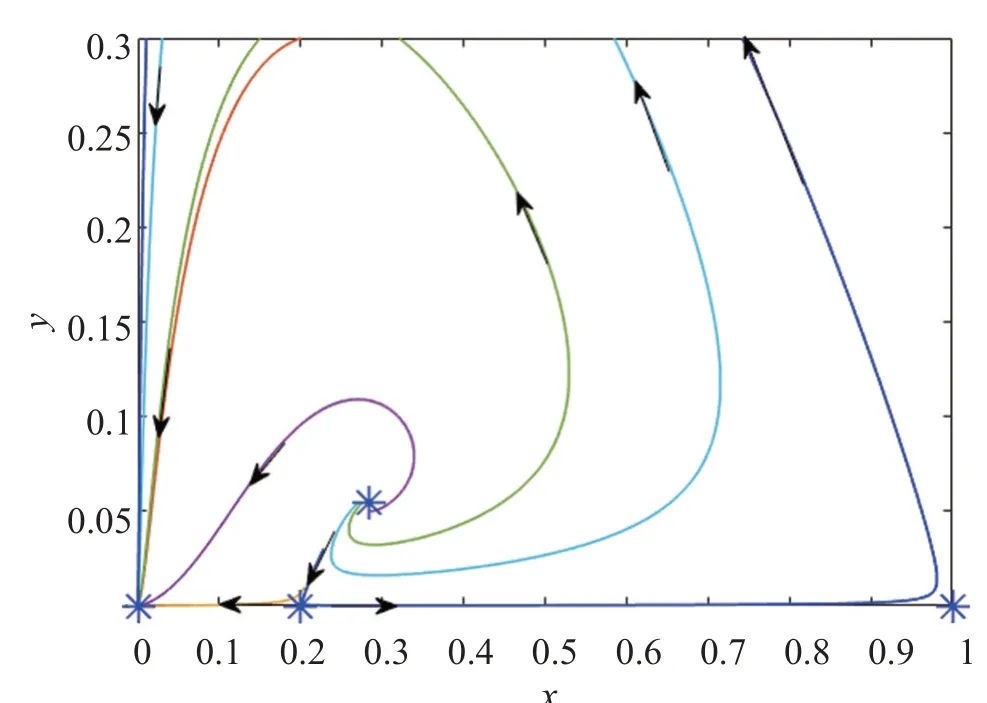
图2 内部平衡点和灭绝平衡点稳定性

在定理4的条件cb＞m下，选取一组参数a=2，b=0.5，e=2，c=1，m=0.4，则边界平衡点E0(0,0)，E1(0.5,0)和E2(1,0)如图3中星号点所在位置，其对应的相图轨线如图3所示。由图3可知，E0是稳定的结点，E1是不稳定的结点，E2是鞍点。

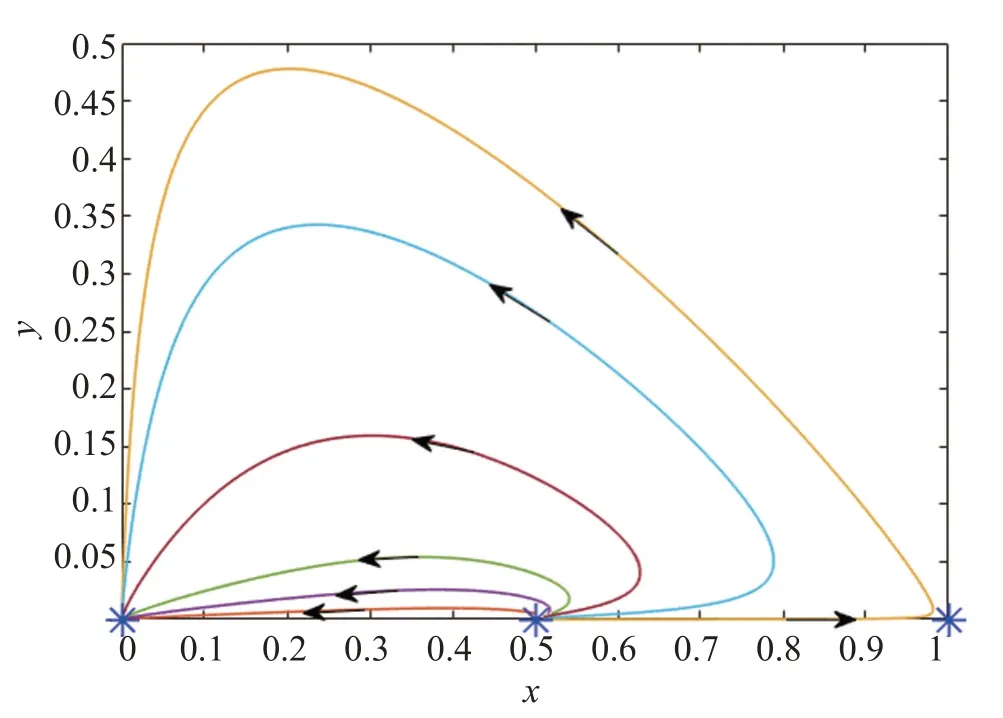
图3 灭绝平衡点稳定性

2.2 内部平衡点的存在性和稳定性

方程组（4）在定理1的条件cb＜m＜c下，选取一组参数a=1，b=0.2，e=1，c=1，m=0.3，记方程组（4）的第一个和第二个方程分别为Function1和Function2，Function1和Function2在这组参数下的图像如图4所示，它们在第一象限内系统（2）只有唯一一个交点。由图4可以清楚地看到，第一象限内系统（2）只有一个内部平衡点。

图4 唯一内部平衡点

借助Matlab 计算可知，这个内部平衡点是E3（0.284 5，0.054 4），Tr(JE3)=0.1857 ＞0，det(JE3)=0.0216 ＞0，平衡点E3附近的相图轨线如图5所示。由图5可以看到，E3是个不稳定的结点，这和定理5的结论一致。

图5 唯一内部平衡点不稳定

方程组（4）在定理2 的条件a(1-b)＞1，m＞c或m＜cb下，选取一组参数a=10，b=0.1，e=1，c=2，m=2.5，Function1 和Function2 在这组参数下的图像如图6 所示，它们在第一象限内有两个交点。由图6可以看到，第一象限内系统（2）有两个内部平衡点。

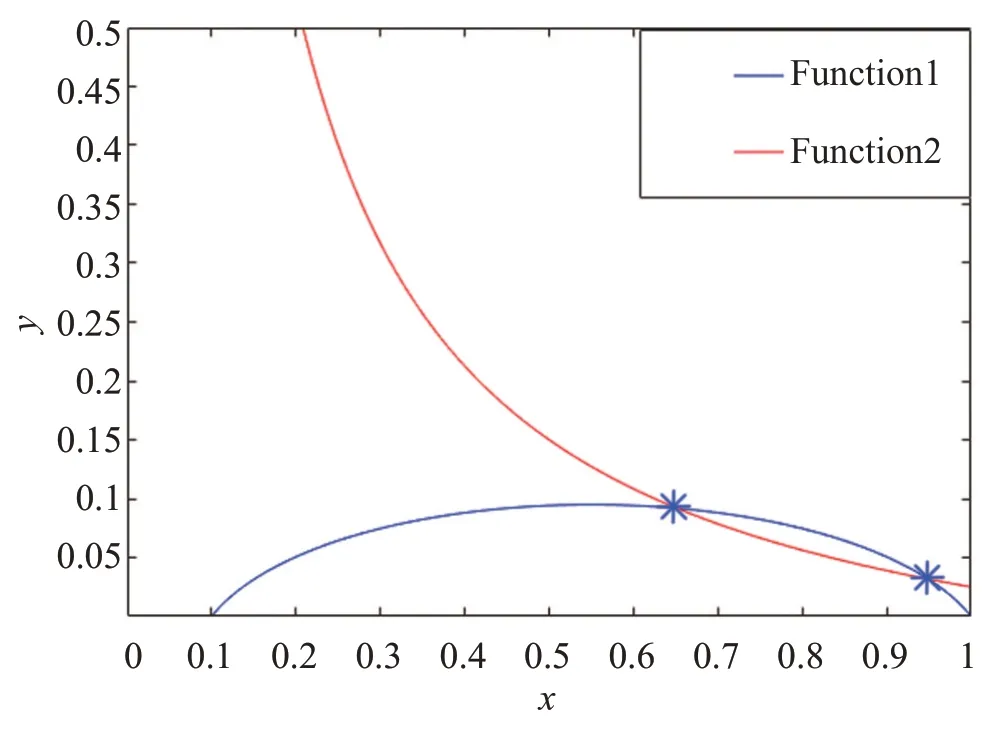
图6 两个内部平衡点

借助Matlab 计算可知，这两个内部平衡点分别是E4（0.651 8,0.091 7）和E5（0.949 3,0.031 6），Tr(JE4)=1.074 7 ＞0，det(JE4)=0.5413 ＞0 和det(JE5)=-0.308 8 ＜0，它们的相图轨线如图7 所示。由图7可以清楚地看到，E4是不稳定的结点，E5是鞍点，这和定理5的结论一致。

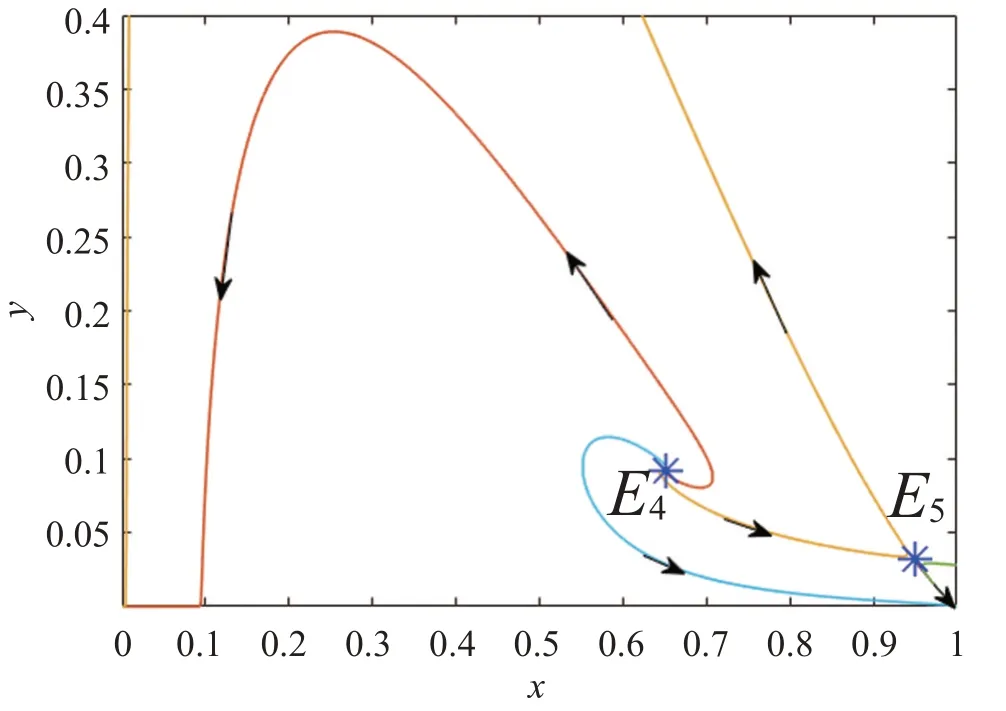
图7 两个内部平衡点的稳定性

3 结束语

综上所述，本文建立了一类具有恐惧效应和Allee效应的合作捕食系统，分析并研究了平衡点的存在条件和稳定性条件。从生态学角度来看，在具有恐惧效应和Allee效应的合作捕食系统中食饵与捕食者是可以共存的，避免了两个物种其中一个灭绝或同时灭绝的情况发生。生物学中食饵与捕食者共存意味着生物的多样性得以保留。生物的多样性是生态平衡的主要因素，也是世界万物繁衍生息的首要条件，生物多样性同样是人类社会得以生存和发展的根本。那么从这个角度来看，保护了生物的多样性就等于保护了人类自身。