基于时频特征的Wi-Fi手势识别技术

任梦恬，田增山，蒋 青

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

随着二十一世纪科学技术的飞速发展以及计算机的普及，人机交互技术已经成为了大家关注和研究的对象[1]。手势是最简单与自然的交互方式，在智能家居[2]、辅助汽车控制系统[3]等诸多领域发挥重要作用，因此，手势识别逐渐成为人机交互的一个重要研究方向。

目前，被广泛关注的手势识别技术主要有基于可穿戴传感设备[4-5]、基于计算机视觉[6-7]、基于射频信号[8-9]3类。其中，基于可穿戴设备和计算机视觉的手势识别系统起步较早，迄今为止已经非常成熟，并且取得可喜的精度[10]，但由于基于可穿戴设备的手势识别系统需要使用者佩戴如数据手套、臂环、加速度传感器等传感设备获取相应的参数，造成使用者的不便；而计算机视觉的方法利用摄像头获取用户手势行为，其依赖于高分辨的视频或图像，并且在黑暗、浓烟等非光照条件下无法使用。与其他手势识别技术相比，射频信号中基于Wi-Fi信号的手势识别系统因其不需要光照、佩戴设备，也不需要昂贵的硬件基础，只需要利用软件的升级与更新，所以逐渐成为手势识别的主流。

基于Wi-Fi的手势识别系统中，目前大多数系统通常使用接收信号强度指示(received signal strength indicator，RSSI)捕捉信号，2014 年，哥延根大学的S.Sigg等[11]提取了RSSI信号对简单的行为进行识别；2015年，H.Abdelnasser等[12]提出WiGest，通过分析RSSI信号变化的上升沿、下降沿等特性进行手势识别，在单个接入点的情况下准确率为87.5%，但RSSI作为一种粗粒度的信号，在不确定噪声和室内多径情况下稳定性比较差，因此，无法提供足够的可靠性。随着对可靠性的追求越来越高，具有更细腻度的信道状态信息(channel state information，CSI)逐渐出现在大家的视野。2013年Q.Pu等[13]提出了基于CSI的手势识别系统WiSee，WiSee通过从Wi-Fi信号中提取人体运动的多普勒频移信息，对推手、挥手类动作进行识别，手势识别平均准确率可达到94%，但由于WiSee系统只能在软件无线电平台上使用，不能在目前商用Wi-Fi上使用，无法进行推广；2015年深圳大学研究出WiG[14]系统，WiG系统基于3发2收的场景，利用滤波抑噪、时域统计特征值等处理，对CSI信息进行手势识别，在直射径环境下准确度达90%以上，但该系统采用了大量的时域统计特征，并且需要对CSI相位信息进行长时间的校正；WiGeR[15]系统基于CSI对手势动作选择动态时间扭曲算法进行识别与分类，手势识别精度均在90%以上，但动态时间规整算法时间复杂度很高，时间开销巨大，并且需要结合k-最近邻(k-nearest neighbo，KNN)分类算法进行分类。相较于传统的时域技术，本文研究增加频域特征频谱熵的信息，手势动作在各个频率分量的变化更加直观，更好地描述了行为的结构特性，同时，本文还采用CSI幅值信息，无需利用功分器对CSI相位信息进行长时间的校正。本文将充分利用CSI幅值信息对{画圈、前后、左右、上下、挥手}5种手势进行识别，具体贡献可归纳如下。

1)针对如何在复杂环境下提取有用的手势信号，本文采用了小波变换-主成分分析联合去噪的方法，在去噪的同时解决了多个CSI子载波之间信号冗余的问题。

2)针对如何完成对手势信号的训练和分类，本文首先提出基于最小方差的信号分割算法对信号进行分割，其次结合时域和频域特征将动作的持续时间、不同频率阶段的频谱熵等特征作为手势的特征值，完成不同手势信号的训练和分类。

1 系统模型与方案设计

室内环境复杂多变，存在着多径效应的干扰，如墙面、沙发、桌椅等静态反射物，其模型示意图如图1。

图1 室内环境示意图Fig.1 Schematic diagram of indoor environment

根据图1可知，接收机接收到的CSI数据为多条路径信号的叠加，可表示为

H(fi,t)=|H(fi,t)|×arg(H(fi,t))=

(1)

(1)式中：|H(fi,t)|和arg(H(fi,t))分别表示第i个子载波在第t时刻的幅值与相位，其中，fi表示子载波的频率；e-j2πΔft表示由于相位误差造成的相位偏移；N为一共的多径数；ak(fi,t)表示第k条多径的传播衰减；e-j2πfiτk(t)表示由于传播时延引起的相位偏移；n表示噪声。

文献[16]根据(1)式推导出CSI幅值的平方公式为

(2)

由(2)式可得，CSI幅值的平方是由一些常量和余弦函数组成，可以准确反映目标运动的抖动性，因此，本文考虑利用CSI幅值信息的特征完成手势运动的分类与识别。系统方案如图2。

图2 手势识别算法系统方案流程图Fig.2 Overview of the gesture recognition algorithm system

2 基于时频分析的手势识别

2.1 数据预处理

由前文可知，接收机接收到的CSI数据为多条路径信号的叠加，存在墙壁、桌椅等静态反射物的干扰，如何在复杂的室内环境中提取目标用户手势运动引起的信号变化是一项巨大的挑战。针对此问题，本文对CSI幅值信号采用离散小波变换(discrete wavelet transform，DWT)技术对信号进行有效去噪；由于CSI信号具有30个子载波信息，但30个子载波携带的信息是有冗余的，并且考虑所有的子载波数会增加计算的复杂性，因此，本文将DWT去噪后的信号进行主成分分析(principal component analysis，PCA)，对数据进行有效降维，进一步达到去噪的效果。

小波变换具有细腻的多尺度信号分析功能，将信号分为细节系数{β(1)，β(2),…,β(J)}和近似系数α(J)，J表示小波变换的层数，每一层的细节系数与近似系数的求解式为

J∈Z

(3)

l∈{1,2,…,J}

(4)

(3)—(4)式中：xn表示输入的信号；〈·〉表示点积运算；g和h表示小波变换的正交基即小波基。因此，重构后的信号为

(5)

(5)式中，细节系数{β(1)，β(2),…,β(J)}中包含手势运动的细节信息以及噪声，针对此问题，本文采用小波硬阈值去噪，将低层的信号噪声置零重构信号。CSI数据处理具体步骤如下。

步骤1从接收机采集手势信号的CSI数据，并提取相应的原始CSI幅值信号subCSI。

步骤2将原始幅值信号subCSI每个子载波经过小波分解，分解层数为5，得出最高层的近似系数α(5)以及各层的细节系数{β(1)，β(2),…,β(5)}。

步骤3采用硬阈值去噪，将细节系数{β(1)，β(2),…,β(5)}置零，根据(5)式重构手势信号subCSI′。

步骤4信号subCSI′的大小为30×p，30为CSI子载波的数量，p为总的采样包数，采用PCA对去噪后的数据进行降维，根据文献[14]可知，降维后第一主成分几乎包含了所有的手势运动信号的信息，因此，得到降维后的信号sig，其大小为1×p。

通过以上4个步骤对信号进行去噪降维处理，其中，手势挥手的数据处理图如图3。由图3可知，采用DWT-PCA联合去噪能有效完成对CSI数据的处理。图4表示挥手手势去噪之后前3个主成分示意图，由图4可知，第1主成分和第2主成分所含噪声较小，而第3主成分噪声较大，第1主成分相对于第2主成分能更好地表示手势信息，因此，采用第1主成分作为降维后的手势信息。

图3 CSI数据处理流程图Fig.3 Flow char of CSI data processing

2.2 基于最小方差的分割算法

由于接收到的CSI手势序列是一个连续的时间序列，要想完成手势的特征提取与分类，需要对接收到的时间序列进行分段处理，同样的动态手势会产生幅度相似的CSI片段。针对这个问题，本文采用基于片段方差最小的方式对连续的时间序列进行分割，5种手势分割后如图5。

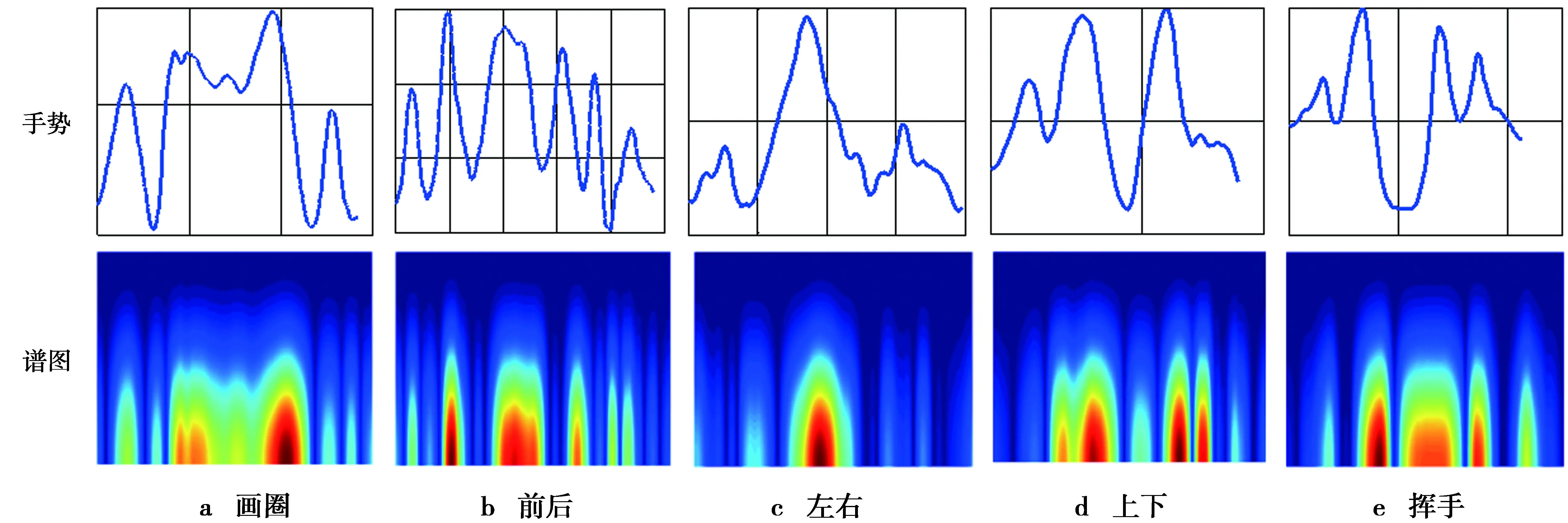
图5 5种手势对应的信号波形图与时频图Fig.5 Signal and time-frequency diagrams five gestures

基于最小方差的分割算法的伪代码如下。

输入：连续动作的时间序列。

输出：连续时间序列的单个手势片段。

算法步骤：

for对每个连续的时间序列

1) do

2) 第一个窗口对应着时间序列的开始，第二个窗口的开始对应着第一个窗口的结束；

3) for每个手势片段

4) 初始化窗口大小Wmin、Wmax；

5) forw=Wmin∶Wmax

6) 得到第一个窗口CSI数据为

Pfirst=(P1,P2,…,Pw)，

第二个窗口CSI数据为

Psecond=(Pw+1,Pw+2,…,P2w)；

7) 计算方差差异

8) end

9) 得到|wmax-wmin+1|对数据(w,d)，其中d值最小的窗口就是我们所求的分割片段；

10) end until直到没有可用于分割的片段；

end

2.3 时频特征提取

2.3.1 短时傅里叶变换

对不同手势信号进行相同特征值的提取以便手势的训练与分类，但手势是一种小幅度的运动，如何从不同手势提取可分辨的特征是关键点，针对此问题，本文采用短时傅里叶变换(short-time Fourier transform，STFT)对信号进行时频转换，在小幅度的行为动作中，短时傅里叶变换的频谱特征相比于小波变换具有更优越的性能[17]。

2.3.2 特征值提取

虽然时域信号与频域信号能很好地反映不同手势运动的特征，但由于时间序列的不一致，大多数的模式识别方法不可行，基于此问题，本文提出了特征值的选取。选取的特征值共6种，如表1。

表1 选择的特征值Tab.1 Selected features

文献[14]使用了时域特征的均值、标准差、方差、四分位距等特征值进行行为的识别，但由于手势幅度较小，这些统计特征值不具有代表性。针对此问题，本文将每个手势运动的标准差、四分位距以及持续时间作为时域特征值。标准差能很好反映手势信号基于均值的离散程度，比均值更具有代表性；四分位距反映了信号中间50%数据的离散程度，不受极值的影响；由于每个动作的时间有差别，因此，每个动作的持续时间也作为特征值。

针对频域特征，常规的算法使用频域信息的均值、标准差等特征值作为手势分类的标准，本文提出了不同频率范围下频谱熵作为特征值，频谱熵是一个标准化的特征值，可以很好地描述行为的结构特性，其计算式为

(6)

2.4 SVM分类算法

支持向量机(support vector machine, SVM)算法是N.Cristianini, J.S.Taylor在1995年提出的一种以结构风险化为准则的模式识别方法，对小样本的处理有突出的优势，主要思想是找到最优的分离超平面可以最小化误差成本函数，从而扩大了分离超平面的边界，完成分类[18]。SVM算法最初只用于解决二分类问题，当处理多分类问题时，需要通过直接法或间接法构造多分类，本文采用间接法中“一对一”方法进行分类。SVM算法分为训练和识别2部分，在SVM训练阶段，本文采用高斯径向基函数核函数，各样本的70%样本数构建分类器；在分类识别阶段，让剩下30%的数据构成测试集依次通过这些分类器，通过投票决定它的类别。

3 算法验证与结果分析

3.1 实验环境

为了验证本文算法的可靠性，选择了2种具有代表性的实验测试环境进行验证。测试环境1选择面积大小为57.6 m×51 m的逸夫科技楼楼顶，该环境为室外空旷环境，障碍物比较少，多径分量也较少，发射机与接收机之间距离分别为5，7，10 m；测试环境2为重庆邮电逸夫楼504为实测环境，逸夫楼504是典型的室内复杂环境，面积大小为7.7 m×9 m，环境中存在墙壁、桌椅等静态反射物，测试时收发装置距离分别为1，2，2.5，3 m，训练数据与测试数据同为{画圈、前后、左右、上下、挥手}5种手势，其测试示意图如图6。

图6 室内室外测试场景示意图Fig.6 Test scenario diagram in indoor and in outdoor

3.2 实验结果分析

针对如图6的实验环境，本文从以下3个方面进行结果分析：①验证分割算法的有效性；②分析采样率对识别精度的影响，并基于2种测试环境验证不同距离情况下算法的有效性；③基于相同数据集验证本文算法与文献[14]中的WiG系统进行比较分析。

基于最小方差的分割算法对不同速度下的挥手手势分割如图7。由图7可知，基于最小方差的分割算法对挥手手势行为进行较为准确的分割。

图7 不同速度下手势分割示意图Fig.7 Gesture segmentation diagram of different velocity

图8是分析采样率对本文算法识别精度的影响，对“画圈”“前后”“左右”“上下”“挥手”5种手势各100组共计500组构建分类器与测试样本，在室内收发相距2.5 m的情况下，对手势分别在采样率分别为200 ，400，800，1 000 packet/s情况下的识别精确度进行评估，并使用了3 倍交叉验证计算分类精度。图8展示了5种手势在不同采样率下的识别精度。

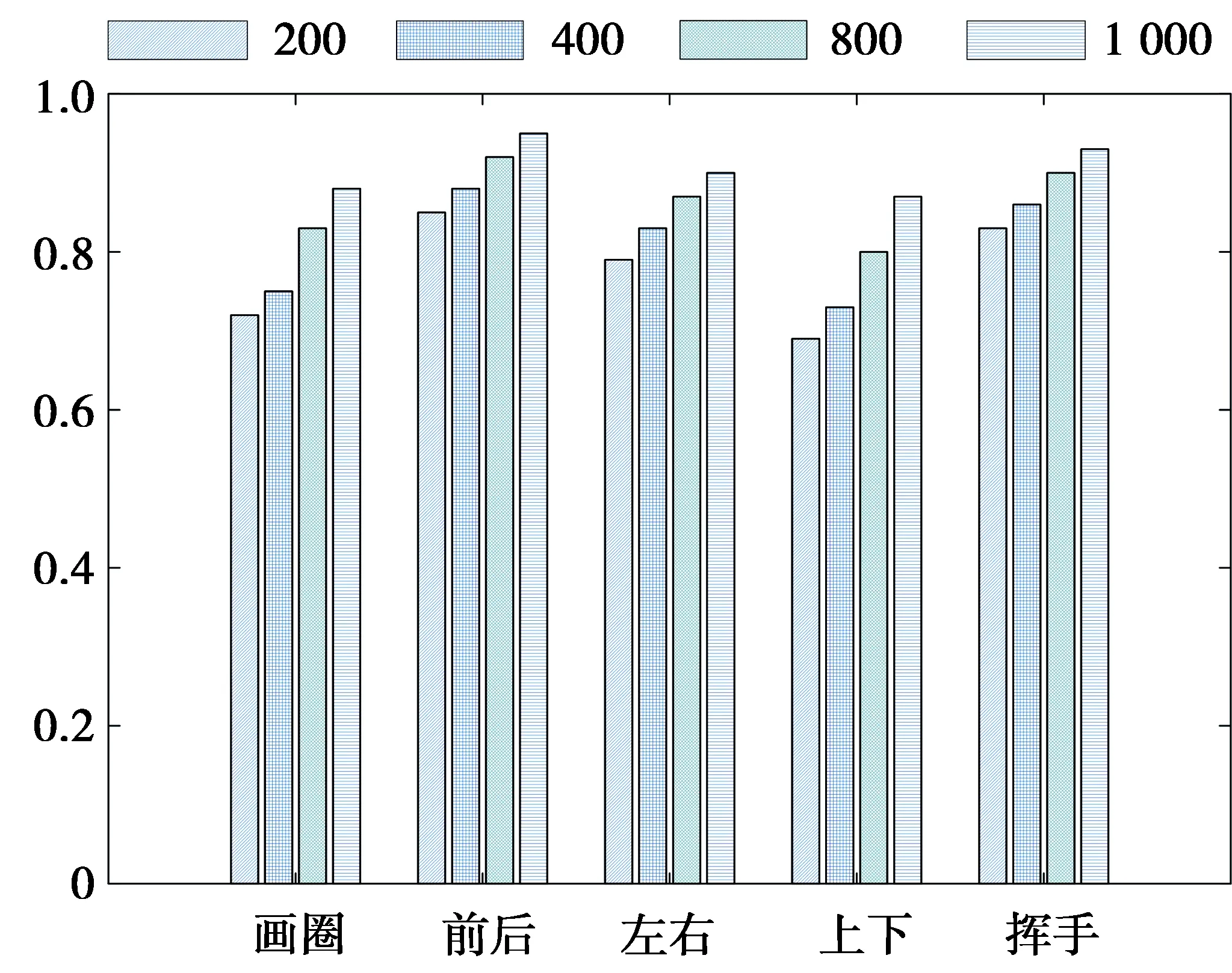
图8 不同采样率下手势识别结果Fig.8 Gesture recognition results under different sampling rates

从图8中可以看出，采样率的增大提高了系统的识别率，因此，本文考虑设备性能以及系统的运行效率，设置采样率为1 000 packet/s。图9是在该采样率情况下的不同场景与位置的识别精度。在不同位置，5种手势各采集100组构建分类器与测试样本。

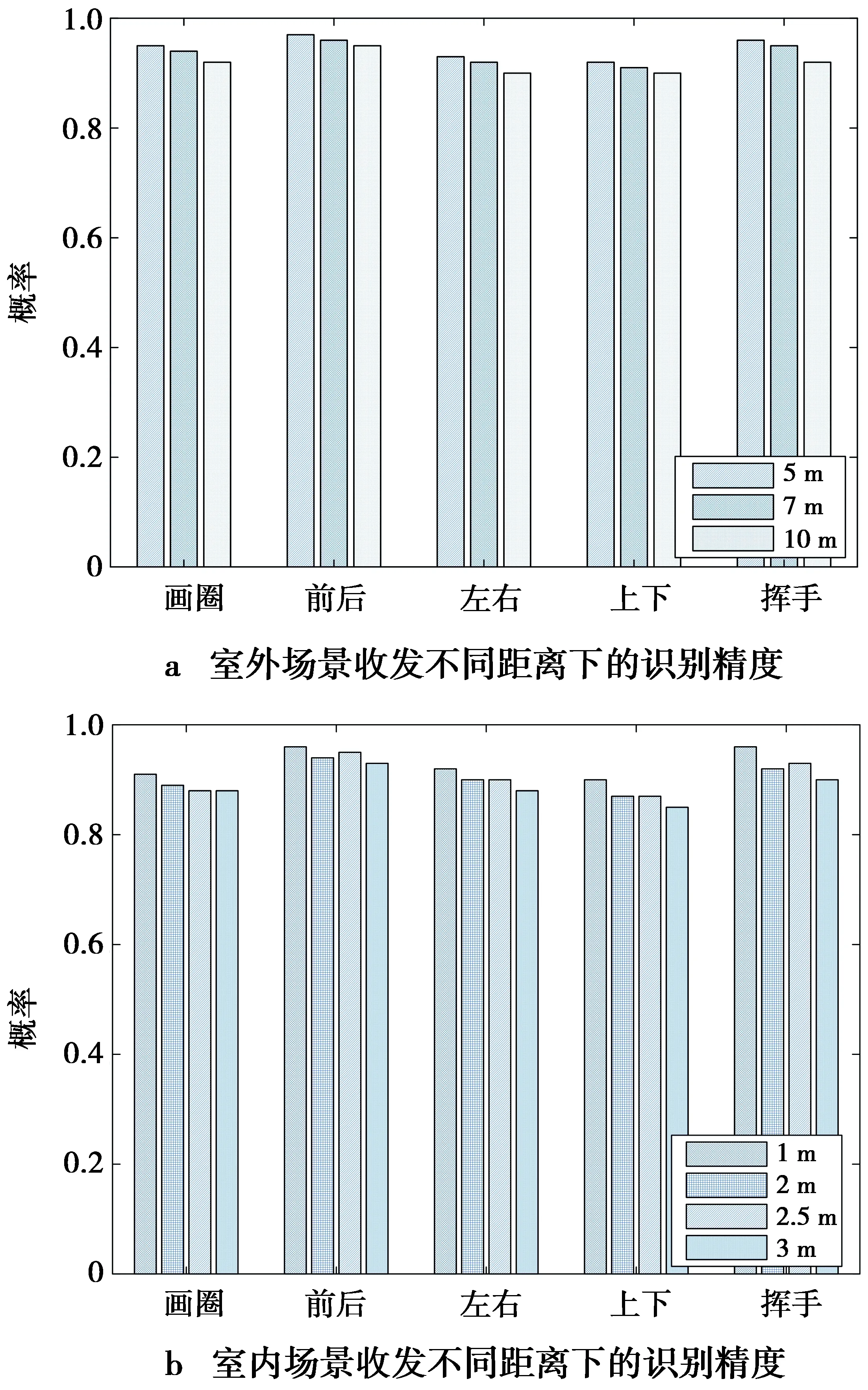
图9 不同场景不同距离下手势分割示意图Fig.9 Recognition accuracy of indoor and outdoor at different distances

图9的结果表明，本文在室外空旷环境下，当收发端距离相隔分别为5，7，10 m时，5种手势的识别率均达到90%以上；室内多径环境下，5种手势在收发端距离相隔分别为1，2，2.5，3 m时，识别率均在90%左右。同时，由于信号在空中的衰减，收发两端距离增大将导致识别率降低。相对来说，手势“前后”和“挥手”具有较高的识别精度，而“画圈”和“上下”手势识别精度相对较小，原因在于“前后”和“挥手”手势相对于“画圈”和“上下”对直射链路的影响较大，特征更为明显。

基于相同测试集与相同的参数设置，收发距离相距2.5 m，本文算法与WiG系统提出的算法对比如图10。从图10中可以看出，对于WiG只提取时域特征的系统，本文提出的算法要优于WiG系统。

图10 本文与WiG系统的对比图Fig.10 Comparison between this paper and WiG system

4 结束语

本文提出了一种基于时频域特征值的Wi-Fi手势识别方法。首先，本文针对如何在复杂环境下提取有用的手势信号，采用了小波变换-主成分分析联合去噪的方法，在利用小波变换去噪之后，采用PCA解决了多个CSI子载波之间信号冗余的问题，进一步抑制噪声；其次，针对传统Wi-Fi时域特征进行手势识别的方法，本文将时域特征值与频域特征值相结合，增加了频谱熵作为特征值，更好地描述了手势行为在频率分量的结构特性，仅仅只需6 个特征即可完成手势的识别。实验结果表明，本文在复杂的室内环境和室外环境均能有效对手势进行识别，手势的识别率达到90%以上。