基于改进蚁群算法的二维码移动机器人路径规划方法

张 毅，李 奎，黄 超

(重庆邮电大学 先进制造工程学院，重庆 400065)

0 引 言

随着国家经济的发展以及对机器人领域的重视，国内移动机器人技术发展相当快，也渗透到各个行业中[1-2]。根据移动机器人的导引方式不同，有激光导引、电磁导引、视觉导引、惯性导引、二维码导引等。由于二维码导引有成本低、柔性高、定位准确、累积误差小等优点，本文主要对二维码导引的移动机器人在结构化栅格工作环境下的路径规划展开研究。

移动机器人路径规划一直是机器人学重要研究内容，在过去20年里，国内外许多学者就此展开了广泛而深入的研究，主要的研究内容是机器人基于不同导引方式、不同工作环境、不同优化目标下的路径规划问题。传统的路径规划有A*算法和Dijkstra算法，A*算法在环境复杂的时候不一定能规划出最优路径，Dijkstra算法的实质是广度优先搜索，时间和空间复杂度较高。近年来，许多群体智能算法应用在移动机器人路径规划中，包括神经网络算法[3]、遗传算法[4]、粒子群算法[5]、人工势场法[6]等，这些算法应用在不同的环境中也有明显的缺点和不足，例如人工势场法容易陷入局部最优，遗传算法适用于全局路径规划，但是运行速度不快，神经网络算法收敛速度慢，计算复杂，内存占用大。蚁群算法在解决移动机器人路径规划问题中是一种更成熟更有效的群体智能算法，它有启发式搜索、鲁棒性强、分布式计算、信息正反馈等优点，但也有收敛速度慢、容易陷入局部最优和停滞现象等缺点。

蚁群算法是由意大利学者Dorigo受生物进化机理的启发而提出的一种群体智能算法，由最初的理论研究延伸到其他具体的应用领域，针对蚁群算法在实际应用中存在的问题，学者们纷纷提出了各种改进方法。文献[7]提出了添加双向搜索机制和比例系数引导因子的启发函数，克服传统蚁群算法易陷入局部最优且收敛速度慢的影响。文献[8]定义了一种新的动态搜索诱导算子，设计了动态搜索模型，加快蚁群算法的收敛速度。文献[9]通过消除蚁群算法禁忌表限制，引入临时权重矩阵，解决景区多景点的路径规划问题。文献[10]设计了一种新的信息素强化机制，利用动态信息进行路径优化，在获得解决方案的多样性和提高算法收敛速度方面都有不错的效果。文献[11]通过改进蚁群算法信息素更新策略，动态调整衰减系数，提高算法的收敛速度。文献[12]将蚁群算法和A*算法结合开发一种双层算法，在密集障碍物的3D环境下实现路径规划。

在结构化工作环境下，机器人只能在水平和垂直方向上移动，机器人走过的路程是当前点到下一个点的曼哈顿距离，直接将蚁群算法应用在此环境下存在停滞、收敛慢的问题，为了使蚁群算法能在结构化工作环境下快速规划出一条最优路径，本文对蚂蚁的搜索方向进行了限制，引入自适应期望函数和启发因子，给出具体的算法表达式以使算法能为此环境下的机器人规划出可行路径，最后引入转弯影响因子，得到扩展路径最小的最优路径。实验结果验证了本文改进蚁群算法的可行性和准确性。

1 蚁群算法环境模型

将二维码移动机器人的结构化栅格工作环境设定为二维平面上一个有限区域，如图1，每一个格子就是一个二维码，在二维码上分布着有限个静态障碍物(图中有黑色圆点的格子)。图1中的数字表示每个二维码的ID，起始点和目标点分别为S和T，本文路径规划的优化准则是综合算法收敛速度、路径长度和转弯情况寻找一条从起始点到目标点的最优路径，结构化环境下机器人只执行前进，左转90°和右转90°动作。例如，机器人在56号二维码上，车头朝着57号二维码，则它下一步可以到达46号、66号或57号二维码。

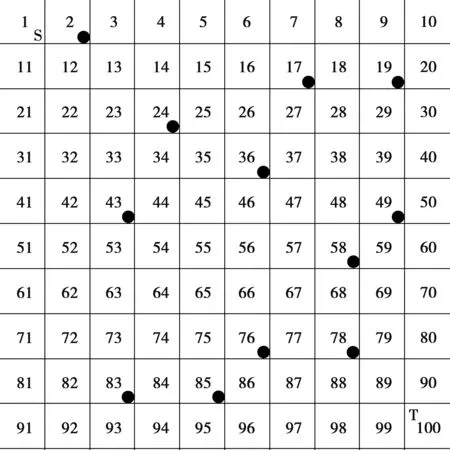
图1 二维码栅格地图Fig.1 Two-dimensional code grid map

设机器人的工作区域由R行C列组成，序号为N的二维码在环境栅格的行号和列号分别为i，j，记为G(i,j)，则可得表达式

i=[(N-1)/C]+1

(1)

j=(N-1)modC+1

(2)

2 蚁群算法基本原理

根据仿生学家长期研究发现，蚂蚁有能力在没有任何可见的提示下找出从蚁穴到食物源的最短路径，并且能在环境变化时搜索新路径，产生新的选择。

蚂蚁集群中的个体之间以及个体与环境之间的信息传递大部分是依赖于信息素进行，它是一种蚂蚁产生的化学物质。蚂蚁在所经过的路径中留下信息素，并且能够感知路径中已存在的信息素浓度[12]。信息素会随着时间的推移逐渐挥发，这一特性可增加蚁群搜索空间，可一定程度避免算法过早收敛于局部最优解。

一条路径上的信息素浓度越高，被其他蚂蚁选择的概率也就越大，从而该路径上的信息素浓度进一步增强，因此，由蚁群的集体行为表现出一种信息正反馈现象。蚂蚁个体之间就是通过这种间接的通信机制达到协同搜索蚁穴到食物源的最短路径的目的[12]。

2.1 概率选择

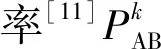
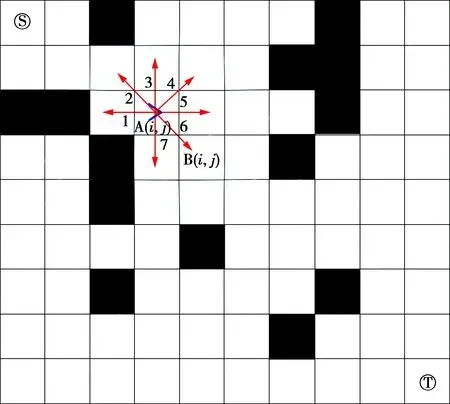
图2 栅格环境模型Fig.2 Grid environment model

(3)

ηAB=1/dAB

(4)

(4)式中，dAB为A到B的欧式距离。

2.2 信息素更新过程

随着时间流逝，信息素会慢慢挥发，用ρ表示信息素挥发系数，满足0<ρ<1，则1-ρ为信息素残留程度，当经过n个时刻，所有蚂蚁构建好路径后，各边上信息素强度进行更新，表示为

τAB=(1-ρ)·τAB+ΔτAB

(5)

(6)

(7)

3 改进的蚁群算法

3.1 引入自适应期望函数

蚁群算法是一种智能启发式算法，启发因子对算法的性能有很大影响[14]。图2传统蚁群算法的启发因子ηAB是A点到B点的欧式距离的倒数，在二维码移动机器人结构化栅格环境中存在一定缺陷，二维码移动机器人位于图2中的位置A，则机器人下一步可以选择的方向只有1，3，5，7，为了确保最快到达目标点，机器人应该尽可能选择5，7的位置，离终点T更近。为了增大相邻节点间概率选择的差距引入自适应期望函数，对相邻节点的期望函数进行不同比例的放大，改善搜索的结果，ηAB表示为

(8)

(8)式中：ω是期望系数；R为地图的行数；C为地图的列数。ω可以表示为

ω=1/LB

(9)

针对结构化工作环境特点，定义(9)式LB为点B到终点T的曼哈顿距离，即

LB=|iT-iB|+|jT-jB|

(10)

3.2 引入启发因子

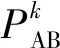
(11)

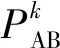
3.3 引入转弯影响因子

机器人在转弯时需先减速再加速再减速，转弯次数太多，严重影响机器人运行效率。所以最短路径不一定是机器人实际运行的最优路径，应该考虑路径的平滑程度。降低二维码移动机器人的转弯次数将提高机器人运行效率。本文将机器人运行路径的扩展长度定义为

L=LA+λn

(12)

(12)式中：L是机器人扩展路径长度；LA是路径的实际长度；λ是影响因子；n是转弯的次数。

3.4 算法流程

本文算法流程如图3，步骤如下。

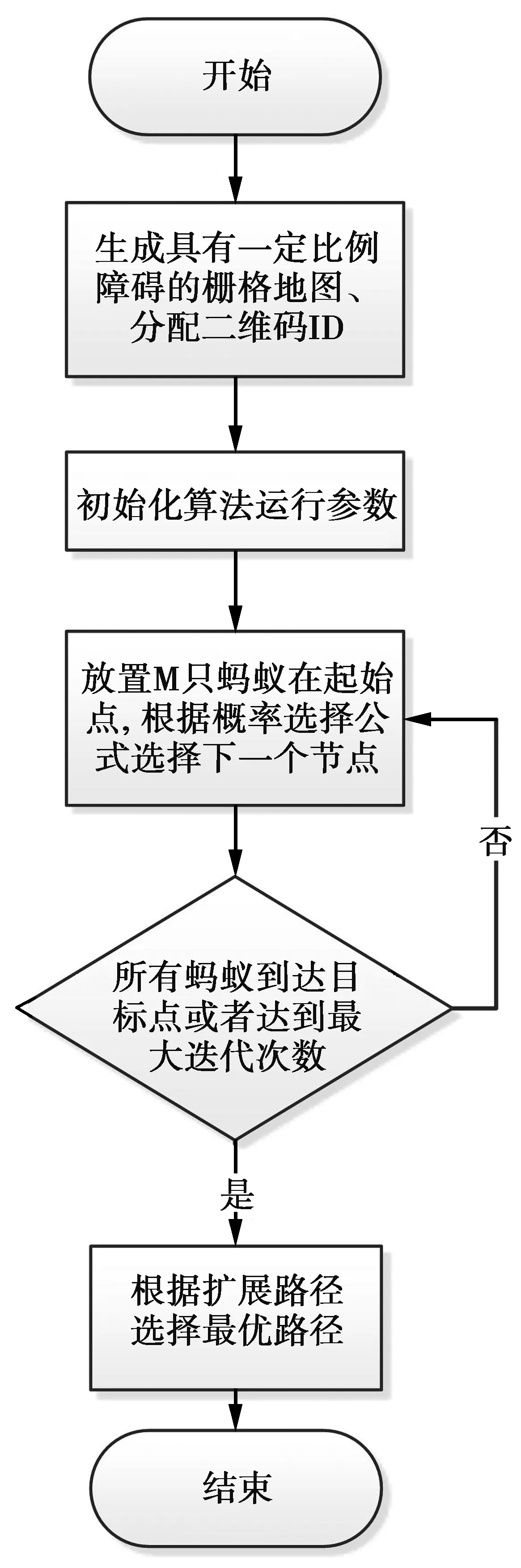
图3 改进算法流程图Fig.3 Flow chart of improved algorithm

步骤1生成已知障碍物分布的栅格地图，给每个栅格分配二维码ID，初始化算法的各个参数，设置起始点、目标点、蚂蚁数量和最大迭代次数。

步骤2放置M只蚂蚁在起始点，并将起始点添加到禁忌表中，蚂蚁k按照(11)式选择下一个可行节点S，如果S是可以选择的，则蚂蚁移动到节点S并将S添加到禁忌表中。

步骤3若蚂蚁k在节点S发生死锁，当前节点可行域为空，蚂蚁无法选择下一个可行节点，则删除蚂蚁k，令k+1→k，转到步骤2，重复步骤2，直到所有蚂蚁到达目标点或者达到最大迭代次数，执行步骤4。

步骤4计算所有到达目标点的蚂蚁的路径长度，并记录其经过的节点，以及转弯次数。

步骤5将得到路径长度以及转弯次数根据(12)式进行筛选，输出最优路径。

4 实验

4.1 仿真

本文所有的仿真实验都在MATLAB中实现，并在Core i3-2120 CPU 3.3 GHz PC上运行，操作系统是window7。仿真实验分别在15×15,30×30,50×50栅格环境中验证算法。经过多次选择与比较，仿真实验中参数设置如下：ρ=0.2，α=2，β=8，Q=1，蚂蚁数量M=50，迭代次数K=200，λ=0.5。

传统蚁群算法，文献[7]算法与本文改进蚁群算法的路径规划图、收敛图分别如图4—图9，仿真实验数据如表1。针对不同复杂度的环境模型进行仿真实验，在指定大小的栅格地图中随机生成障碍物。从实验结果中可以得出，本文改进的蚁群算法在有解的结构化栅格环境下能得到最优路径。

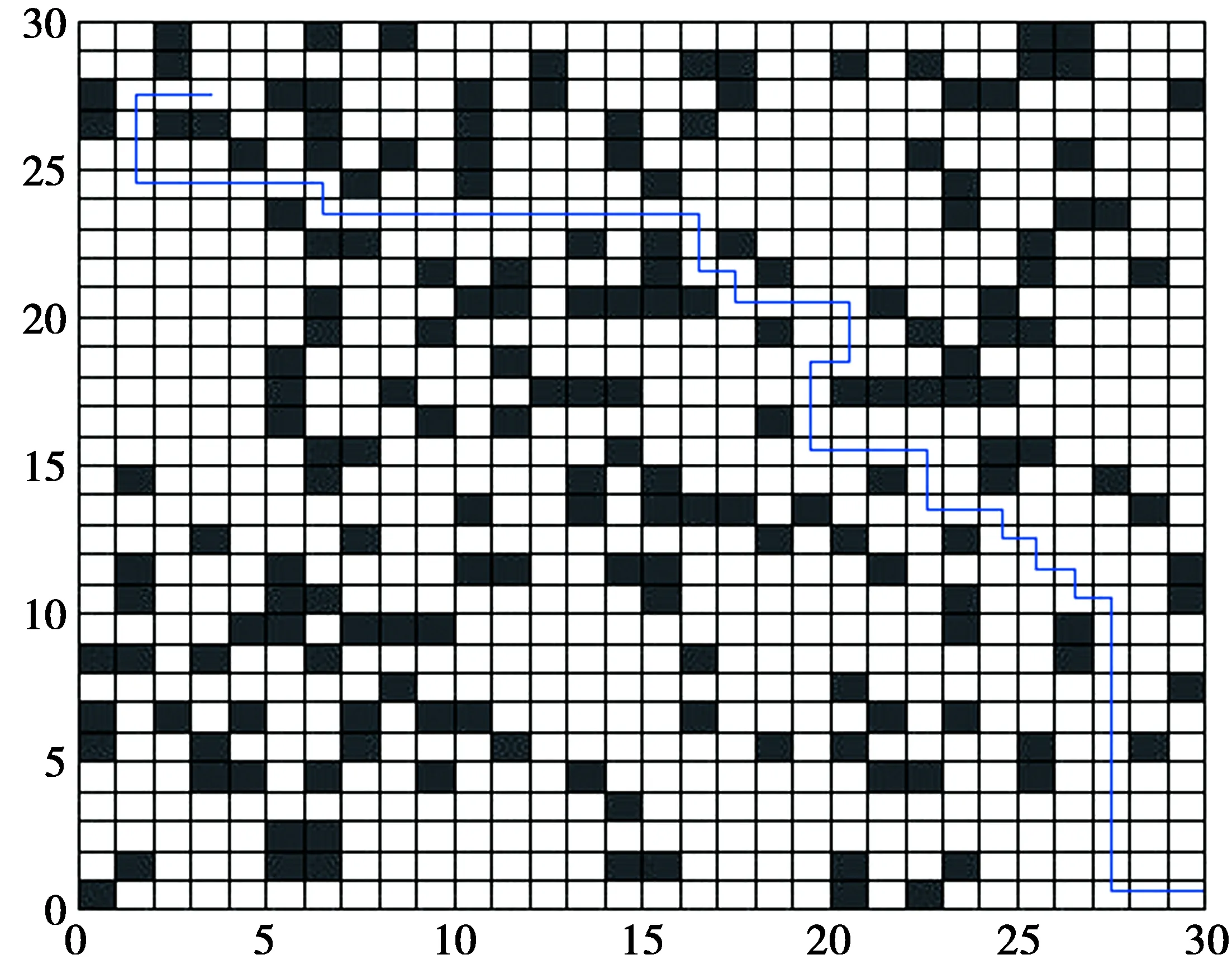
图4 传统蚁群算法路径规划图Fig.4 Path planning graph of traditional ant colony algorithm

图6 本文改进蚁群算法路径规划图Fig.6 Improved ant colony algorithm path planning graph in this paper

图7 传统蚁群算法收敛图Fig.7 Convergence graph of traditional ant colony algorithm

图8 文献[7]蚁群算法收敛图Fig.8 Convergence graph of reference[7]

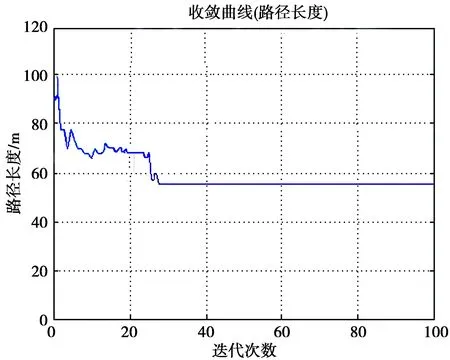
图9 本文改进蚁群算法收敛图Fig.9 Improved ant colony algorithm convergence graph in this paper

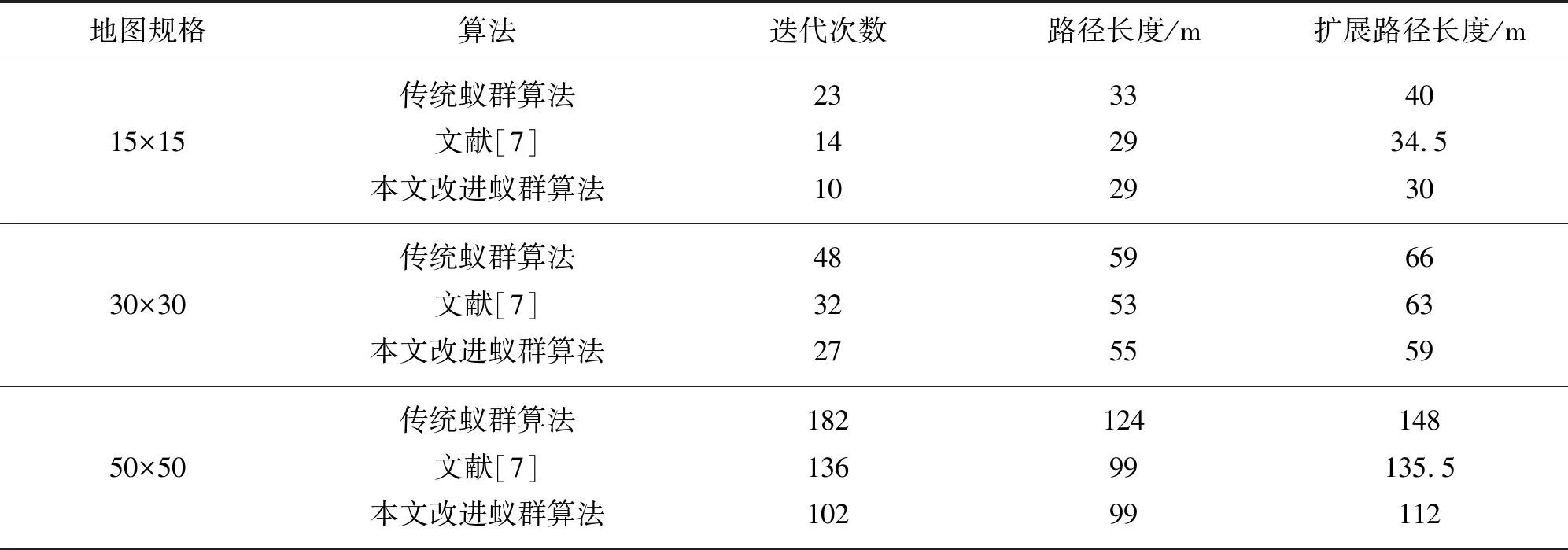
表1 仿真实验数据Tab.1 Simulation experiment data

4.2 二维码移动机器人实验验证

实验在15×15的栅格地图中进行，机器人的主控芯片采用STM32F407IGT6，二维码选用DM码，二维码间距为500 mm，相机扫描DM码获取位置信息，将信息通过以太网传输给单片机，上位机分别采用仿真实验中的3种算法为机器人规划路径，算法参数和仿真实验设定参数一致，通过WiFi将规划出的路径信息传送给单片机，设定机器人运行速度为0.6 m/s，机器人根据接收到的路径信息移动。实验结果如表2和图10。实验结果和仿真结果一致，验证了本文改进算法的可行性和准确性。

表2 路径规划实验结果Tab.2 Experimental results of path planning

图10 二维码移动机器人路径规划实验Fig.10 Path planning experiment of two dimensional code mobile robot

5 结论

本文提出了一种基于改进蚁群算法的二维码移动机器人全局路径规划方法，针对实际情况，将蚂蚁可以选择的方向限制在当前节点的上下左右4个方向，引入自适应期望函数和启发因子，算法可以有效避免停滞状态，并快速找到从起始点到目标点的可行路径，根据机器人的运动特性，在转弯过程中需要先减速再加速再减速，要耗费一定时间，因此，本文引入转弯影响因子，使目标函数更合理。实验结果证明，在二维码构建的结构化栅格环境下，本文改进的蚁群算法可以快速找到从起点到目标点的最优路径。