应急场景下基于可靠无线通信的D2U功率控制机制研究
程传彬,吴鹏飞,黄 俊
(1. 重庆邮电大学 通信与信息工程学院,重庆 400065;2. 重庆邮电大学 计算机科学与技术学院,重庆 400065)
0 前 言
作为应急通信的有效解决方案之一,终端直连通信(device-to-device,D2D)技术受到了业界的广泛关注[1]。D2D技术最早由3GPP Rel.11所定义,即设备与设备之间允许复用蜂窝频谱进行直连通信。当发生自然灾害而导致基础设施(如电力设施和通信设施等)损毁时,利用D2D通信可完成应急区域的数据交互和环境监测,从而大大缩短灾害应急救援时间[2-3]。
然而,D2D通信技术在应急环境下也面临诸多技术挑战。一方面,终端设备能量受限,无法满足长时间、数据量大的传输需求;另一方面,灾害区域的通信环境一般较为复杂,无法保证可靠通信(如同频干扰、距离过远等)。近几年来,随着能量采集技术和无人机技术的发展,上述两大问题得到了一定程度的缓解。使设备在环境中采集能量并与无人机建立通信连接,则有望在应急场景下实现可靠通信[4-5]。
如何利用D2D或者D2U通信技术保障应急场景下的可靠通信是当前研究的热点。文献[6]研究了毫米波链路之间交互所引发的吞吐量低和时延高问题,作者试图通过重传机制来解决上述问题。但该机制引入了额外的能耗开销。文献[7-8]设计了无人机(unmanned aerial vehicle,UAV)辅助模式下功率控制算法来提高D2D通信速率,可以在一定范围内提高通信质量,但未能引入重传机制,进一步提高应急场景中可靠通信。文献[9-10]设计了功率控制算法来优化UAV与D2D设备之间的中断概率,从而节省UAV能量,延长服务时间,但并未考虑应急场景下D2D设备的能量,控制发射功率。在文献[11]中,作者推导出基于混合自动重传请求协议的丢包率闭式表达式,通过仿真,作者分析了能量采集概率对丢包率的影响。但作者并未对丢包率进一步优化。文献[12]提出了基于全局和在线的2种功率控制策略以提高快衰落模型下链路的吞吐量。然而,2种功率控制算法存在复杂度相对较高的问题。文献[13-14]研究了与瞬时获取能量状态无关的功率控制方法来降低中断概率。然而,在实际场景中,设备发射功率与设备瞬时获能后的可用能量具有相关性。在文献[15-16]中,作者分别利用贪婪算法和几何规划法设计了基于自动请求重传的功率控制策略。但上述工作均假设重传过程中的数据包与重传确认(ACKnowledgement,ACK)不会丢失,这显然与实际情况不符。
通过总结上述相关工作发现:①在应急场景中,无线通信的可靠性一般用丢包率来衡量;②利用重传技术可降低通信丢包率,从而保证通信可靠性;③功率控制是保障可靠通信的有效手段;④基于重传技术设计功率控制机制时必须充分考虑重传所带来的能耗以及重传ACK丢失的情况。
为此,本文提出UAV辅助模式下基于自动重传请求(automatic repeat request,ARQ)的功率控制机制来实现应急场景下的可靠传输。具体而言,首先通过分析数据包与ACK的接收失败概率得出D2U通信失败率;其次,在快衰落和慢衰落2种模型下定义通信失败率优化问题。针对优化问题,设计功率控制迭代算法。该算法充分考虑了重传所带来的能耗以及重传ACK丢失的情况。仿真实验结果表明,本文所设计策略的通信失败率低于其他策略。
1 系统模型
1.1 系统场景
假设在某应急场景下有N个无线设备,记为D={Dn,n=1,2,…,N},通过UAV与外部通信并且设备可利用能量采集技术从环境中获取能量,以延长待机时间。另外,UAV主要维持可靠通信,为了避免应急场景下设备之间的同频干扰,采用了正交频分复用的技术,如图1。

图1 应急场景中基于能量采集和ARQ的D2U通信Fig.1 D2U communication with energy harvesting and ARQ in emergency scenarios
设备与UAV通过传输控制协议(transmission control protocol,TCP)中的ARQ技术来保证可靠通信,主要通过上层来优化下层,即,UAV当接收到某设备的数据包后返回ACK,若该设备成功接收ACK,则认为该设备与UAV通信成功,否则通信失败。
设D2U的传输在长度为T的一个时隙完成,分为2阶段:①设备发送数据包到UAV;②UAV成功接收到数据包立刻返回ACK到设备。同时,假设设备Dn一个单位的时间帧包含Ln个时隙,即数据包最多可重传的次数为Ln,亦即一帧的时长为Tf=LnT。若数据包或ACK在某时隙传输失败,设备Dn则重传该数据包,若经过Ln次重传后,数据包或ACK仍未被正确接收,则认为通信失败。
1.2 能量管理模型
由系统模型可知,设备Dn所消耗的能量为发送数据包消耗的能量,而UAV所消耗的能量为发送ACK消耗的能量。设备Dn能量获取的模型可视为独立同分布(independently identically distribution,IID)的伯努利分布[15],即设备Dn在某时隙里以概率αn获取能量E。
设备Dn在某一帧内重传数据包的功率策略为
(1)

(2)
设备Dn在某一时隙里重传数据包所消耗的能量应小于其剩余能量(剩余能量包括获能和电池剩余能量),即Bn(ln)·E≥mn(ln)·E,这里,Bn(ln)为设备Dn在第ln时隙起始时刻的剩余能量容量[15]。因此,设备Dn的剩余能量容量为
Bn(ln+1)=min{max{0,Bn(ln)+E-
(3)

1.3 通信中断概率

中断概率是表征应急场景下通信可靠性的重要指标。若设备Dn在第ln时隙里重传数据包的功率为pn(ln),UAV对设备Dn发送ACK的功率为pu,n,那么,在设备Dn发送数据包到UAV阶段中数据包接收失败概率为
(4)
(4)式中:Pr[·]表示概率;SNRn,u(ln)表示第ln时隙UAV接收端的信噪比值;γu为UAV接收信噪比阈值,高斯白噪声功率谱密度N0=1。
在UAV发送ACK到设备Dn阶段中ACK接收失败概率为
(5)
(5)式中:SNRu,n表示设备Dn接收端的信噪比值;γn为设备Dn接收信噪比阈值。
因此,设备Dn在第ln时隙里通信中断概率为
(6)
2 问题描述
2.1 通信失败率分析
在上节中,通过(4)—(5)式推导得到了设备Dn在某一时隙里的通信中断概率。基于能量不受限机制[18-19],接下来分析设备Dn在一帧内的通信失败率。
在慢衰落条件中,一帧内所有时隙之间的信道状态相同,衰落服从指数分布。那么,若设备Dn以某功率重传的数据包未被正确接收,在该条件下设备Dn以较低的功率发射也会通信失败,此时设备Dn在下一时隙将以较大的功率发射,保证通信成功,即重传数据包的功率满足pn(1) 证明由pn(1) (7) 在快衰落条件中,一帧内时隙之间的信道状态服从IID,且衰落服从指数分布。设备Dn在一帧的时隙里重传数据包的功率依次为pn(1),pn(2),…,pn(Ln)。 定理2设备Dn在快衰落信道中通信,通信失败率PDn为 (8) (8)式中,Ln表示重传的次数。 证明在快衰落条件中,一帧内所有时隙之间的信道状态满足IID。所以,其通信失败率由各个重传的通信中断概率的乘积所决定。 由于不同衰落条件下通信失败率不同,下面分别从快衰落和慢衰落条件对问题进行描述。 在快衰落条件中,N个设备与UAV的通信失败率PD的优化模型为 (9) 利用泰勒展开式,将上述优化模型转化为 Bn[ln])])≤g ≤1 (10) 该目标函数由N·Ln个问题组成。首先,针对Ln个子问题,设Ru,n为初始值,采用几何规划法,求出局部最优值;然后,由(9)式可知Ru,n和mn(ln)的关系。随着Ru,n值增大,该子问题的目标函数先增大后减小,可设计迭代法求出该子问题的全局最优解;然后,依次求解(N-1)·Ln个子问题,从而得到目标函数的最优值。根据以上思路,设计了如算法1所示的功率控制迭代算法。 算法1功率控制迭代算法 输出N个设备与UAV的最优通信失败率PD=1-Pdd; 1.for 1≤n≤Ndo 3.whilebk-ak>εdo 5.while‖S(p+1)n-S(p)n‖2≤εdo 6.分别用S(p)n来替代公式(10)的T1、T2、T3中分母多项式Ga(Sn),Gb(Sn),Gc(Sn); 9.用几何规划法求解并求得S(p+1)n,p←p+1; 10.end while 12.else转到15; 13.end if 14.ak+1←λk,bk+1←bk,λk+1←μk,μk+1←ak+1+0.618·(bk+1-ak+1),转到16; 15.ak+1←ak,bk+1←μk,μk+1←λk,λk+1←ak+1+0.382·(bk+1-ak+1),转到16; 16.k←k+1,转到3; 17.end while 18.获得设备Dn的最优通信失败率PDn,Pdd←Pdd·PDn; 19.end for 算法1对N个设备的通信失败率依次求得最优解,其中黄金分割法的复杂度为O(logk),几何规划法迭代次数为p,那么该算法1的复杂度为O(N·p·logk)。 在慢衰落条件中,N个设备与UAV的通信失败率PD的优化模型为 M6: 0≤αn≤1 (11) (11)式中:M1为设备Dn一帧内的能量约束;M2为UAV一帧内的能量约束;M3为设备Dn重传数据包的功率系数mn(ln)约束;M4为UAV发送ACK的功率系数Ru,n约束;M5确保设备Dn一帧内时隙数的取值;M6表示设备Dn获取能量概率αn的取值范围。 与2.2小节相比,慢衰落条件下的优化问题需充分考虑重传数据包之间的功率约束,但算法步骤基本相同。 本文用N个设备与UAV的通信失败率来评估端到端的不同状态下D2U的通信性能。表1给出了主要仿真参数。参数值设置参考了文献[4,18,20]。 表1 仿真主要参数Tab.1 Main parameters of simulation 图2显示了不同衰落模型下(快衰落和慢衰落)通信失败率与获取能量概率的Monte Carlo仿真与理论结果对比。图2中,NC表示理论值;MC表示Monte Carlo仿真值。从图2可知,Monte Carlo仿真与理论结果近似相等。由于设备最大储能容量、信道状态变化以及获取能量随机性,它们在数值上存在较小偏差。另外,快衰落条件下趋于平稳的通信失败率相比于慢衰落条件下的要低,进一步验证了理论推导结果((7)—(8)式)的正确性。 图2 不同衰落模型下通信失败率与获取能量概率 的Monte Carlo仿真与理论结果对比 Fig.2 Comparison between Monte Carlo simulations and numerical results in term of PD w.r.t. α1in different fading 由文献[12,15]可知,它们均未考虑ACK是否丢失的情况以及ACK带来的重传能耗影响,文献[15]中策略的丢包率优于文献[12]中策略的丢包率,差距较小,但文献[12]的遍寻策略复杂度极高,甚至不能很好地达到较高的精确度。为了进一步评估本文提出的策略,本文根据文献[12,15]的策略将其改变为3种不同的策略,然后比较他们之间的通信失败率。 策略1和策略2均是在文献[12]的基础上,加入ACK。策略1为全局遍寻等功率策略,用遍寻的方式寻找合适的ACK发射功率和重传的功率,其中重传的功率采用相等的方式;策略2为递增式功率控制策略,用遍寻的方式寻找合适的ACK发射功率和重传的功率,其中重传的功率采用递增的方式。策略3是在文献[15]的基础上,加入ACK。策略3重传的功率采用文献[15]的几何规划法求得,ACK的发射功率根据UAV最大通信消耗能量和时隙数量均等分配。 策略1的算法复杂度为O(N·n·r),其中,n和r分别为重传数据包功率和ACK功率的遍寻次数。策略2的算法复杂度为O(N·n·m·r),其中,m为递增量的遍寻次数,n和r分别为重传数据包功率和ACK功率的遍寻次数,这是由于采用重传功率以递增的方式进行。这2种算法复杂度均高于本文所提策略的算法复杂度。策略3的算法复杂度为O(N·q),其中,q为几何规划迭代的次数。 图3显示了不同衰落模型中(图3a快衰落,图3b慢衰落)通信失败率与获取能量概率在不同策略下的仿真结果对比。由图3可知,随着获取能量概率增大,不同策略的通信失败率均先下降后趋于平稳。随着获取能量概率增大,本文策略的通信失败率先优于策略1和策略2,后趋于相等,优于策略3;其中,从图3a的效果来看,在快衰落模型下,当获取能量概率α1为0.1时,本文策略的通信失败率优于策略2为0.85%,优于策略1为1.93%,优于策略3为1.37%;本文采用106个数据包进行实验,通信失败次数分别相差8 500次、19 300次和13 700次;当获取能量概率α1为0.8时,本文的策略优于策略2为0.000 1%,优于策略1为0.000 9%;本文采用106个数据包进行实验,通信失败次数分别相差1次和9次。其中,在获取能量概率α1较低时,本文的传输失败次数明显优于其他策略,这对提升应急场景的可靠性不容忽视。这是由于当获取能量概率较小时,所能获取到的能量较小,导致可以分配到的功率较小,从而使得策略1和策略2未充分利用完获取到的能量,不能有效地达到最优解;而当获取能量概率较大时,所能获取到的能量较大,导致可以分配的功率也变大,从而策略1和策略2可充分利用获取到的能量,更易逼近最优解。而策略3未充分考虑ACK带来的重传能耗影响,从而未分配适当的功率。 在慢衰落模型下,随着获取能量概率增大,本文策略的通信失败率低于策略2和策略3。其中,从图3b的效果来看,在慢衰落模型下,当获取能量概率α1为0.1时,本文策略的通信失败率优于策略2为6.54%,优于策略3为3.52%;本文采用106个数据包进行实验,通信失败次数相差65 400次和35 200次;当获取能量概率E=12 dB为0.8时,本文的策略优于策略2为0.39%;本文采用106个数据包进行实验,通信失败次数相差3 900次,本文策略优于策略2,应急场景的可靠性得到了很好地提高。这是由于当获取能量概率较小时,所能获取到的能量较小,导致可以分配到的功率较小,从而使得策略2未充分利用完获取到的能量,不能有效地分配各个重传数据包的功率;而当获取能量概率较大时,所能获取到的能量较大,导致可以分配的功率也变大,从而策略2可充分利用获取到的能量,有效地分配重传数据包的功率。 图3 不同衰落模型中通信失败率与获取能量概率 在不同策略下的对比 Fig.3 PD vs. w.r.t. different policies in different fading model, where 图4显示了通信失败率与最大储能容量在快衰落(图4a)和慢衰落(图4b)不同策略下的仿真结果。从图4曲线可以观察到,在2种衰落模型下,通信失败率均表现为先减小随后趋于平稳。这是由于最大储能容量越大,剩余能量越多(根据能量不受限原理),通信成功的可能性就越大,即通信失败率越低。另外,终端设备储能容量通常较大,从图4a可知,当通信失败率趋于平稳时,本文策略与策略1、策略2趋于相等,而策略3劣于其余3种策略。从图4b可知,当通信失败率趋于平稳时,本文策略优于策略1、策略2,而策略3劣于其余3种策略。这是由于策略3未充分考虑重传数据包功率与ACK的功率关系,从而未充分利用完获取到的能量,本文策略与策略1和策略2充分利用获取到的能量,且储能容量较大时趋于相等。 图4 不同衰落模型中通信失败率与最大储能容量 在不同策略下的对比 Fig.4 PD vs. maximum energy storage capacity w.r.t. different policies in different fading model, where E=12 dB,α1=0.7,E=12 dB, 图5给出了不同衰落模型(快衰落图5a和慢衰落图5b)中通信失败率与获取能量概率在不同时隙数量下的仿真结果对比,并且本文策略与其他策略做了对比。图5中,L1表示设备D1一帧内的时隙数量。从图5可知,在2种衰落模型下,时隙数量越大,通信失败率越快趋于平稳。这归因于一帧内时隙数量变大,增加了可重传的次数。当时隙数量变大时,本文策略优于其他策略,这是由于本策略充分利用到获取到的能量,且考虑ACK对重传带来的影响。 图5 不同衰落模型中通信失败率与获取能量 概率在不同时隙数量下的对比 Fig.5 L1=3 different time slots in different fading model, where E=12 dB, 图6显示了不同衰落模型(快衰落图6a和慢衰落图6b)中通信失败率与获取能量概率在不同获取能量下的仿真结果对比,并且本文所提策略与其他策略做了对比。从图6可知,在2种衰落模型下,获取能量越大,通信失败率越低。显然,获取能量增加可使通信中断概率降低,从而降低通信失败率。当获取能量降低时,本文策略优于其他策略,这是由于本策略充分利用到获取到的能量,且考虑ACK对重传带来的影响。 图6 不同衰落模型中通信失败率与获取能量概率 在不同获取能量下的对比 Fig.6 PD vs.α1w.r.t. different energy harvesting in different fading model, where 综上所述,当取不同参数设置时,本文策略优于其他策略,其中策略1和策略2均采用遍寻的方法,导致其复杂度较高,因此,本文策略能更好地凸显出优势。 针对应急场景下通信可靠性低的问题,本文提出了UAV辅助模式下基于ARQ的D2U功率控制策略。利用通信失败率来表示通信可靠性,本文分别在快衰落和慢衰落条件下对通信失败率进行建模,并设计了优化模型与算法。通过Monte Carlo仿真发现,本文提出的功率控制策略相比其他策略具有更低的通信失败率,从而保证应急场景下D2U通信的可靠性。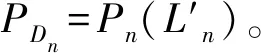
2.2 快衰落下的问题描述



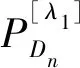
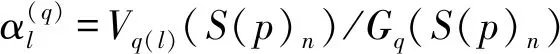


2.3 慢衰落下的问题描述
3 仿真分析






4 结束语

