能量收集通信系统中基于深度Q网络的最大化保密速率功率控制策略

李朝辉，雷维嘉

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

随着通信行业的迅速发展，通信网络对能源供给的需求不断增加，巨大的能源消耗不可避免地产生大量温室气体。寻找新的绿色能源，并合理高效地利用能源成为通信行业发展的关键问题之一。通信网络中的节点从自然环境中收集能量(如太阳能、风能、热能，等)并转化为电能用于信息传输，可减少对传统能源的依赖，是一种对环境友好且低成本的绿色通信方式[1]。由于能量收集量的随机性和间歇性，能量收集通信节点的能量管理和功率分配问题是需要解决的重要问题之一[2]。

根据节点是否事先知道能量到达和信道状态的信息，可以将能量收集通信系统的能量管理模型分为离线管理模型和在线管理模型2类。离线管理模型假设能量收集过程中数据到达情况、收集的能量和信道状态等事先已知。虽然这一假设并不符合现实通信场景，但离线模型下设计的能量管理策略能提供能量收集通信系统性能的理论上限。文献[3-6]对不同场景下的离线能量管理策略进行了研究。文献[3]研究点对点能量收集通信系统的最佳离线功率分配策略，研究的系统模型中的发射机配备能量收集设备收集能量并用于发送数据，该文分别针对直接传输的单跳模型和通过中继节点转发的双跳模型，给出了最大化系统吞吐量的功率分配方案。文献[4]研究了点对点能量收集无线通信系统中的功率调度问题。在能量到达情况事先已知的条件下，控制发送功率最大化一定时间内的吞吐量，并指出该问题与数据量一定时完成时间最小化问题等价。文献[5]考虑了2种场景下能量收集通信系统传输时间最小化问题。在第1种场景下，传输开始之前所要传输的数据包已经到达，而第2种场景下，数据包是在传输期间到达。文献[5]针对这2种场景分别设计了相应的算法来获得全局最优离线功率调度策略。文献[6]在发送端已知能量到达和信道状态的情况下，将非凸的功率控制优化问题转换为凸优化问题，给出了一种有效的离线算法。与离线管理模型中数据到达、收集的能量和信道状态等的具体信息已知不同，在线管理模型中仅知道它们的统计信息。文献[7-8]对在线能量管理策略进行了研究。文献[7]讨论点对点通信系统中传输速率的动态规划问题，提出了一种低复杂度方案，使能量收集发送节点在仅知道能量到达的统计知识的情况下合理分配发送功率，提高系统性能。文献[8]考虑由源节点、目的节点和能量收集中继节点组成的协作通信系统，研究链路选择和中继功率分配的联合优化问题，提出了基于动态规划的策略来最小化中断概率。

在现实的通信场景中，能量收集系统收集的能量、数据的到达过程，以及信道的变化是不确定的，离线的能量管理框架不适用。它们的统计信息也很难获得，因此基于统计信息的在线能量控制策略的使用也受到较大的限制。强化学习是一种自适应在线学习，智能体(agent)在和环境不断交互过程中使学习策略达到回报最大化。文献[9-11]对利用强化学习解决没有环境先验知识的通信系统中的能量控制问题进行了研究。文献[9]考虑发送节点为能量收集节点的点对点通信系统，将发送节点发送功率的优化控制问题转换为强化学习问题，并讨论了强化学习算法的参数对系统性能的影响。文献[10]考虑点对点通信问题，每个节点配备2根天线，发送节点从环境中收集能量用于信息发送。文献将多输入多输出无线通信链路吞吐量最大化问题建模为状态转移概率未知的马尔科夫决策过程(Markov decision process, MDP)，进一步提出了一种Q学习算法来解决该问题。文献[11]考虑点对点能量收集系统。源节点从环境中收集能量用于发送信息，在缺少信道增益和能量收集的先验知识的情况下，提出了一种基于执行者-评论者的强化学习算法来求解功率分配问题。文献[12]考虑三节点的中继系统，其中中继节点为能量收集节点，研究联合时间调度和功率分配问题，提出了一种基于深度强化学习的在线时间调度和功率分配算法。

由于无线通信的广播特性和开放性，它面临的安全威胁比有线通信更严重。传统的安全方法在高层采用加密编码来防止信息被窃取。随着计算技术的发展，传统的加密技术存在失效的风险。物理层安全技术是实现信息安全传输的另一种途径。Wyner在1975年提出了窃听信道模型[13]，定义了保密容量来评估系统保密传输的性能。Wyner的研究表明，当合法信道优于窃听信道时，即使没有任何高层加密措施，理论上合法用户之间的安全通信也是可能的。文献[14]介绍了物理层安全的基本理论，并概述了物理层安全技术的最新工作以及未来的挑战。

本文研究能量收集无线通信系统中，物理层安全传输中优化能量使用效率、最大化保密传输速率的在线功率分配算法。与文献[9-12]不同，本文考虑存在窃听节点的系统的保密速率最大化问题。假定环境状态信息事先未知，系统模型中信道系数、电池电量、收集的能量连续取值。首先将系统模型建模为马尔科夫决策过程，然后采用神经网络近似Q值函数来解决系统状态有无限多种组合的问题，利用反向传播最小均方误差来调整神经网络的参数。最后，提出基于深度Q网络(deep Q network,DQN)的在线功率分配算法，通过对信道状态特性和能量收集特性的不断学习，动态地调整发送节点的功率，优化安全传输的能量效率。

1 系统模型

本文研究由3个单天线节点组成的能量收集窃听信道系统模型下的物理层安全传输中的能量效率优化问题，系统模型如图1。发送节点内含能量收集设备和可充电电池。能量收集设备从周边环境中收集能量并将其用于向目的节点发送数据。传输过程中，发送节点收集的能量是随机变化的，无线信道也是随机变化的。发送节点根据瞬时的信道状态及能量收集情况，以最大化长期时间平均保密速率为目标，动态地调整发送功率，提高能量的使用效率。

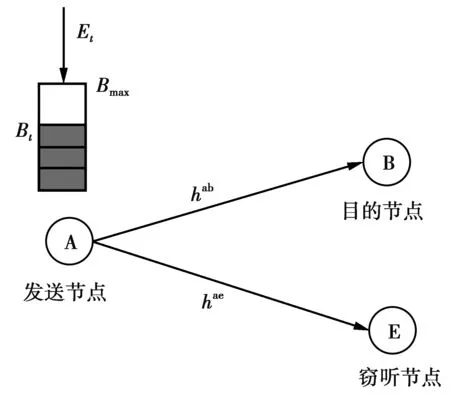
图1 系统模型Fig.1 System model

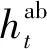
0≤Pt≤Pmax

(1)

同时，该时隙中发送信息的能量应不超过该时隙开始时电池存储的电量，即应满足电池电量使用的因果约束：

τ·Pt≤Bt∀t=1,2,…,T

(2)

(2)式中，τ为一个时隙的时长。在下一个时隙开始时，电池的电量为

Bt+1=min(Bt-τ·Pt+Et,Bmax)

(3)

假设在一个时隙内信道系数保持不变，合法信道和窃听信道的噪声功率相同，服从独立同分布的零均值加性高斯白噪声，方差为σ2，合法信道和窃听信道的信道容量分别为

(4)

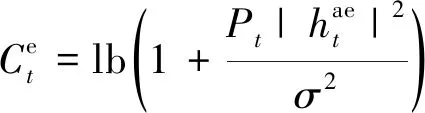
(5)

根据物理层安全的相关理论，当合法信道优于窃听信道时，即使没有任何保密编码，信息的安全传输也是可以实现的[13]。系统的可达保密速率是能实现信息保密传输的速率上限，定义为合法信道与窃听信道的信道容量之差，即

(6)

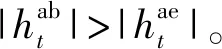
(7)

功率控制的目标是在能量收集和电池使用物理特性的约束下，最大化长期时间平均保密速率，即

s.t. a) 0≤Pt≤Pmax

b)τ·Pt≤Bt

(8)

2 基于DQN的功率分配算法

2.1 强化学习

强化学习[15]是一类机器学习方法，用状态、动作、奖赏来反映智能体和环境之间的相互作用，智能体在与环境的交互过程中不断改善策略来达到最大化收益的目的。强化学习常被建模为由五元组(S,A,T,R,γ)组成的MDP。其中，S为有限的环境状态集合；A为智能体可以选择的动作集合；T为状态转移函数；R为回报函数，表示在状态st下，智能体选择动作at后，环境反馈给智能体的奖赏；γ∈[0,1]为用来计算累积奖赏的折扣因子。

对于一个MDP，强化学习的最终目标是找到完成任务的最优策略。策略为智能体在某个状态下与执行动作间的映射，通常用符号π表示，即

at=π(st)

(9)

对于一个给定的策略π，累积奖赏定义为

(10)

(10)式中，Rt为在状态st执行动作at的奖赏。由于同一状态下选择的动作可能不同，因此某一状态的累积奖赏不是一个特定值，而是一个预期值。用状态-动作值函数(简称为Q函数)来表示给定策略下累积奖赏的预期值：

(11)

(11)式中，E表示对策略π的Gt求数学期望。根据贝尔曼方程，累积奖赏可按(12)式计算[16]。

Q(st,at)=Eπ{Rt+γQ(st+1,at+1)|s=st,a=at}

(12)

(12)式中，st+1表示状态st执行动作at后转移到的下一状态。智能体在学习过程中不断地优化策略π，最终达到最优策略π*。强化学习的本质是找出每个状态的最佳Q函数，表示为

a=at}

(13)

Q学习[16]是一种基于Q函数估计的强化学习算法，也被称作异策略时序差分(temporal difference, TD)学习算法。它的主要流程为：建立一个以状态-动作对为索引的Q值查找表，在智能体与环境的不断交互探索中更新该表格，最终学习得到一个最优策略。TD目标为目标值函数的估计值，智能体在学习过程中Q函数是向着TD目标更新的。Q函数的更新规则为

Q(st,at)←Q(st,at)+

(14)

(14)式中：Rt+γmaxat+1Q(st+1,at+1)为TD目标；α∈ [0, 1]为学习速率。Q学习算法通过建立和更新Q值表来进行最优策略的学习。当待解决问题的状态空间较小时，Q学习能很好地工作。但是当状态空间和动作空间很大或为连续空间时，值函数无法用表格来表示。为了解决这个问题，可以采用逼近的方法来近似表示值函数Q(st,at)为

(15)

(15)式中，θ为计算动作值函数的参数。值函数的逼近可以分为线性逼近和非线性逼近，利用神经网络逼近值函数是常用的非线性逼近方法。

训练神经网络时，要求训练数据间是独立的，但是在强化学习中得到的数据之间存在相关性，直接用这些数据训练可能导致神经网络不稳定。文献[17]提出了采用双神经网络解决训练不稳定和连续状态空间的DQN算法。DQN使用2个结构相同但是参数不同的神经网络用于计算TD目标和动作值函数，参数分别为θTD和θ。参数θ在学习的每一步都更新，参数θTD每隔固定的步数更新一次。为了破除了学习经历之间的相关性，改善神经网络的训练效率，DQN利用记忆库存储每一个时隙的(st,Pt,Rt,st+1)样本数据，随机从记忆库中抽取样本数据进行学习。

学习过程中更新的是神经网络的参数，常用的更新方法是梯度下降法。(14)式的值函数更新转换为参数θ的更新，即

Q(st,at;θt)]∇Q(st,at;θt)

(16)

(16)式中：θTD为计算TD目标的神经网络的参数；Rt+γmaxat+1Q(st+1,at+1;θTD)为TD目标。

2.2 基于DQN的功率分配算法

本小节中设计基于DQN的在线功率分配算法，最大化图1系统的保密速率。在时隙t，发送节点A根据当前电池电量、收集的能量、合法信道和窃听信道的信道系数选择发送功率Pt使得系统长期时间平均保密速率最大化。定义以下几个关键元素将上述问题映射到Q学习模型。

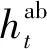
(17)

2)动作集。动作集为发送节点可选择发送功率的集合。为了降低算法的复杂度，设置有限种可选择的功率值，即动作集A为从0到Pmax以步长δ进行取值的集合。由于发送节点可选择的发送功率还受限于当前的电池电量和电池的最大放电功率，所以在时隙t动作集At为

(18)

3)回报函数。立即回报是发送节点选择发送功率Pt时对应的收益，即保密速率，表示为

(19)

由于电池容量有限，如果电池的电量溢出会造成浪费，所以对于电池溢出的情况，设置一个附加函数gt对出现电池溢出的动作选择进行惩罚，表示为

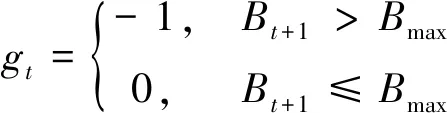
(20)

回报函数为立即回报函数加上附加回报函数，表示为

Rt=rt+βgt

(21)

(21)式中，β∈ [0,1]是用来权衡附加函数的正实数。

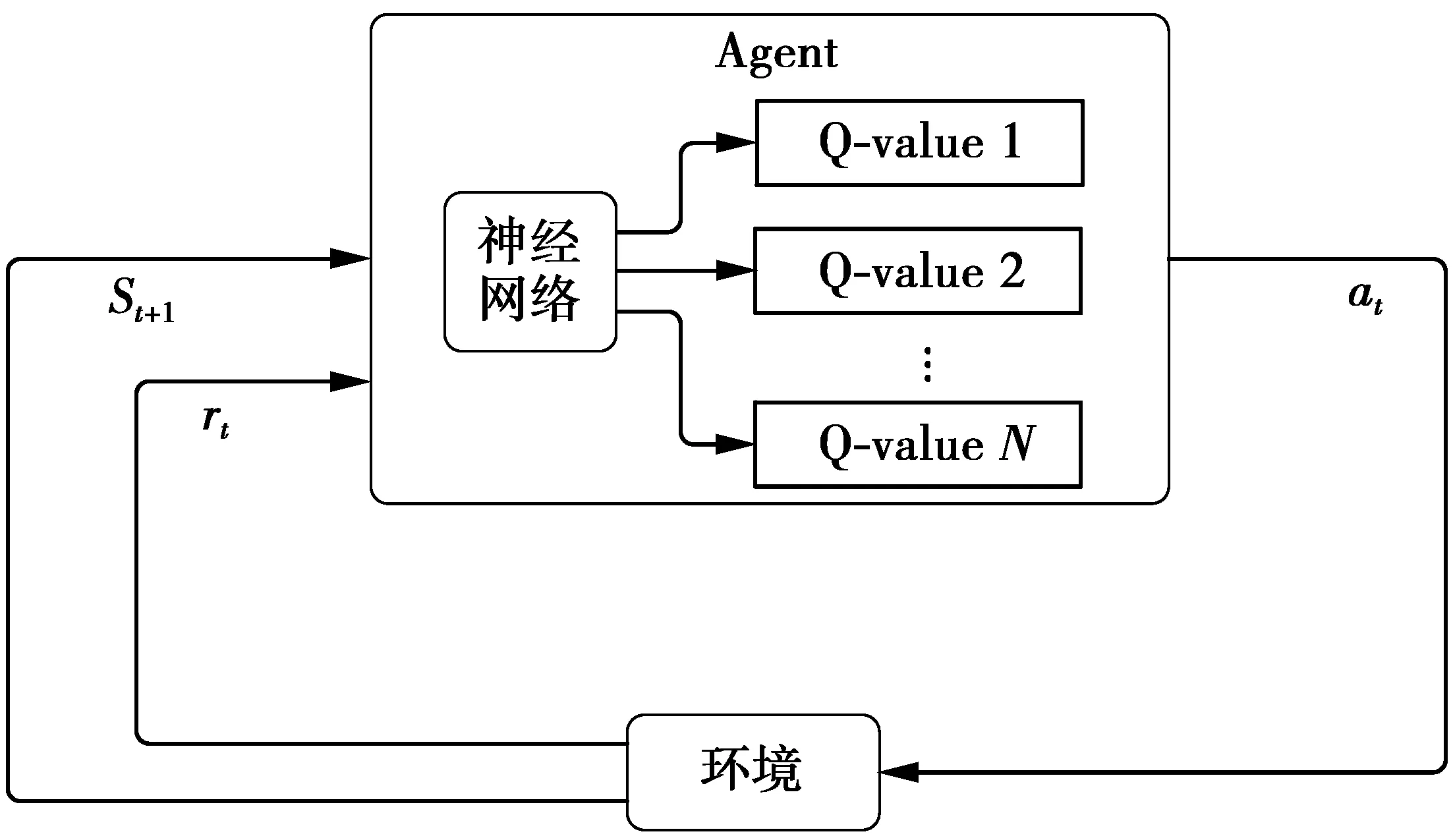
图2 深度Q网络构架Fig.2 Deep Q network architecture

在强化学习训练过程中，有“探索”和“利用”2个选择。“探索”即尝试不同的动作，可收集更多的信息；“利用”则选择目前最优的动作。“探索”有机会发现更高回报的动作，但也可能采用了回报较低的动作，是进取性的行为。“利用”采用当前回报最高的动作，是保守的行为。“探索”和“利用”是相互矛盾的，在总的训练步数一定的情况下，加强了一方就会削弱另一方，因此,学习中需对“探索”和“利用”进行折中。在DQN中，通常使用ε-贪婪策略在“探索”和“利用”之间权衡。在每次进行动作选择时，以ε的概率选择“探索”，以1-ε的概率选择“利用”，即

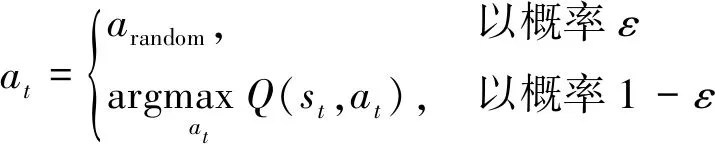
(22)

(22)式中：ε(0≤ε≤1)是对“探索”和“利用”折中的一个参数；arandom表示在状态st下随机选择的动作。一种控制ε的方式为

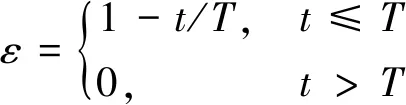
(23)

(23)式中，T为“探索”“利用”阶段时长。在t>T时发送节点每次都选择当前状态下神经网络输出Q值最大的动作。

DQN需要建立一个容量为N的记忆库D来存储每一个时隙的样本数据，随机从记忆库中抽取数量为M的样本数据进行学习，每隔C步将参数θ更新到θTD。基于DQN的在线功率分配算法总结如下。

算法1基于DQN的在线功率分配算法

初始化容量为N的记忆库D

随机初始化Q网络和目标Q网络的参数θ和θTD

t=0

观察初始状态st

Fort≤Tdo

由(22)式选择发送功率Pt

由(21)式得到相应的奖赏

观察下一状态st+1

将(st,Pt,Rt,st+1)存入D中

从D中随机采样(si,Pi,Ri,si+1)计算TD目标yi

以(yi-Q(si,Pi;θ))2为损失函数来训练Q网络

每隔C步，θTD←θ

st←st+1

End for

3 仿 真

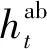
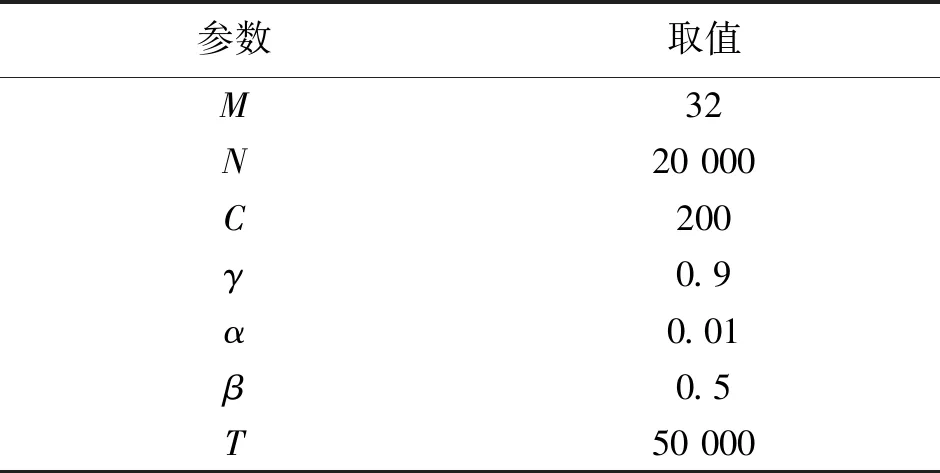
表1 仿真中算法1参数Tab.1 Algorithm 1 parameters in simulation

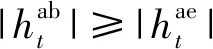
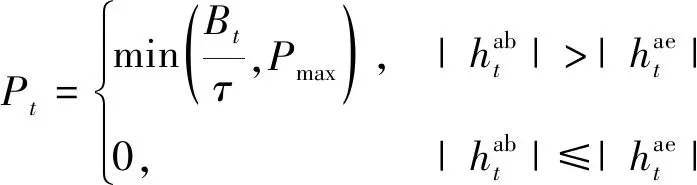
(24)

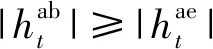
图3给出了本文所提算法以及3种对比算法的保密速率随时间变化的情况。仿真中，设置电池容量为Bmax=15 J，收集能量最大值Emax=1 J。由于信道和能量收集随机变化，每个时隙的保密传输速率也在随机变化，若给出瞬时的保密速率并不能很好地说明算法的性能。为了更好地体现所提算法在各个阶段的性能，我们给出每10 000个时隙保密速率的平均值。由图3可见，对状态空间做离散化处理后的Q学习算法性能提升并不明显。本文提出算法的性能随着时间的推移而提升，在50 000个时隙后，算法平均保密速率优于其他3种算法且基本保持稳定。这是因为随着时间的推移，DQN算法学习到更优的策略并且在动作选择上选择“利用”的概率也越来越大。

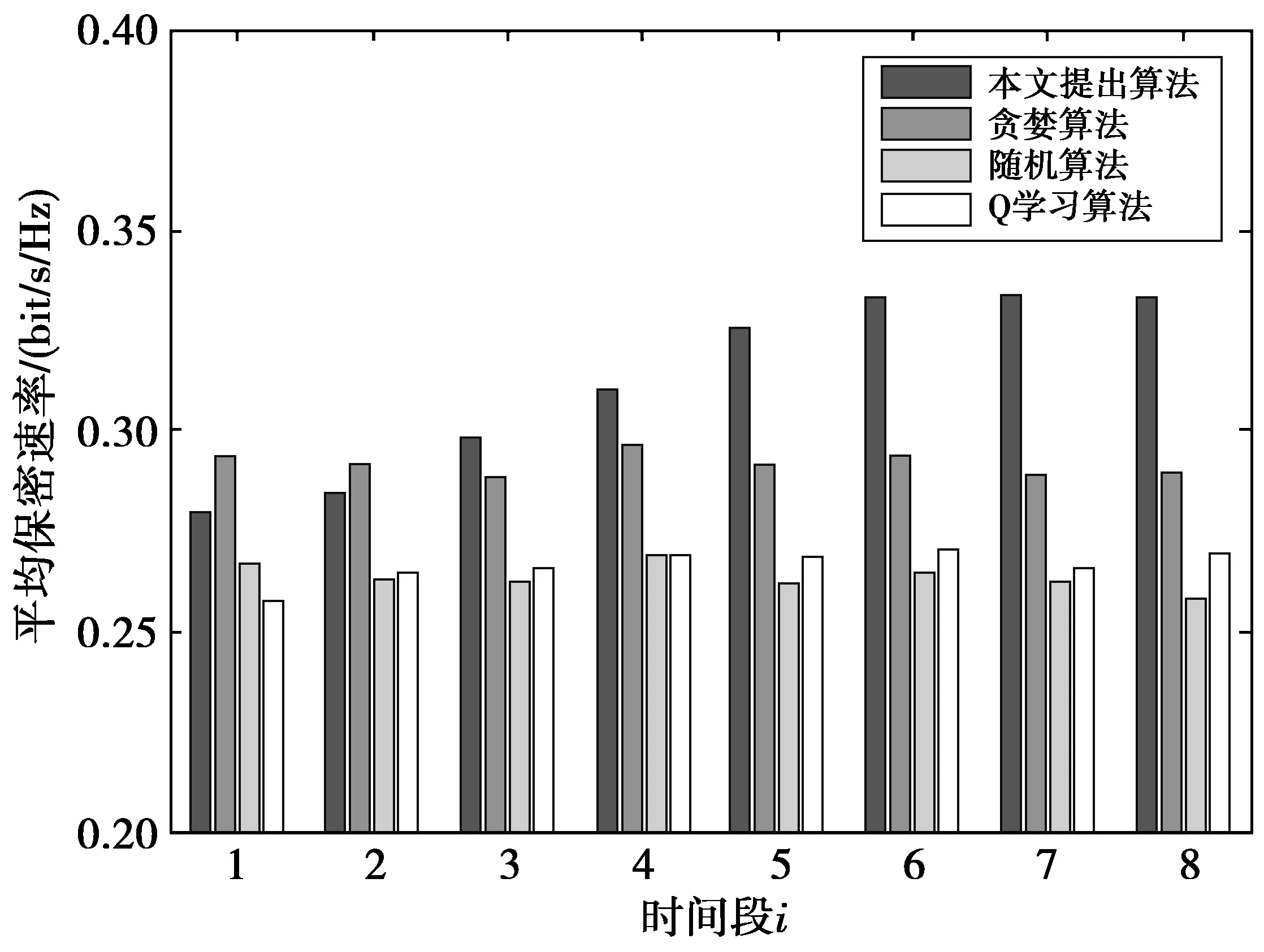
图3 保密速率随时间段的变化情况Fig.3 Secrecy rate changes over time

图4给出了平均保密速率随收集能量最大值Emax变化的曲线。仿真中，设置电池容量Bmax=15Emax。由图4可知，当收集能量的最大值Emax增加时，所有算法的平均保密速率都随之增大，这是因为随着收集能量的增加，发送节点可用于发送数据的能量越多，传输速率就越高。

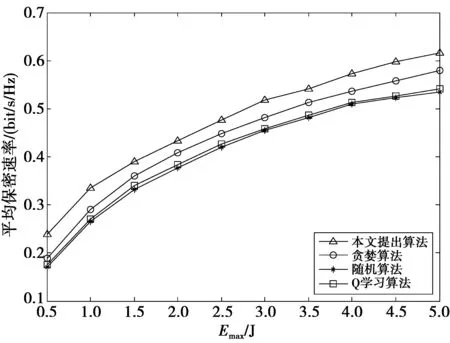
图4 Emax对平均保密速率的影响Fig.4 Emax impact on average secrecy rate

图5给出了不同的电池容量下的平均保密速率。仿真中，设置每时隙收集能量的最大值Emax=1 J。从图5中可以看出，当电池容量很小时，本文所提算法的性能与贪婪算法接近。这是因为在电池容量较低时，容易出现一个时隙中收集的电量大于电池容量的情况。为避免溢出，本文算法中每时隙选择高功率的概率很高，因此与贪婪算法的性能相近。随着电池容量的增加，本文算法中功率的选择空间加大，性能逐渐改善，在Bmax>6.5 J以后，本文算法性能已明显优于贪婪算法。在Bmax>9.5 J以后，所有算法的保密速率基本都不再随电池容量的增加而提升。这是因为Bmax>9.5 J以后，相比较每时隙平均收集的能量，电池容量已足够大，已足够缓存收集的能量供不同时隙间进行能量调度，所以,性能不再随电池容量的增加而增加。

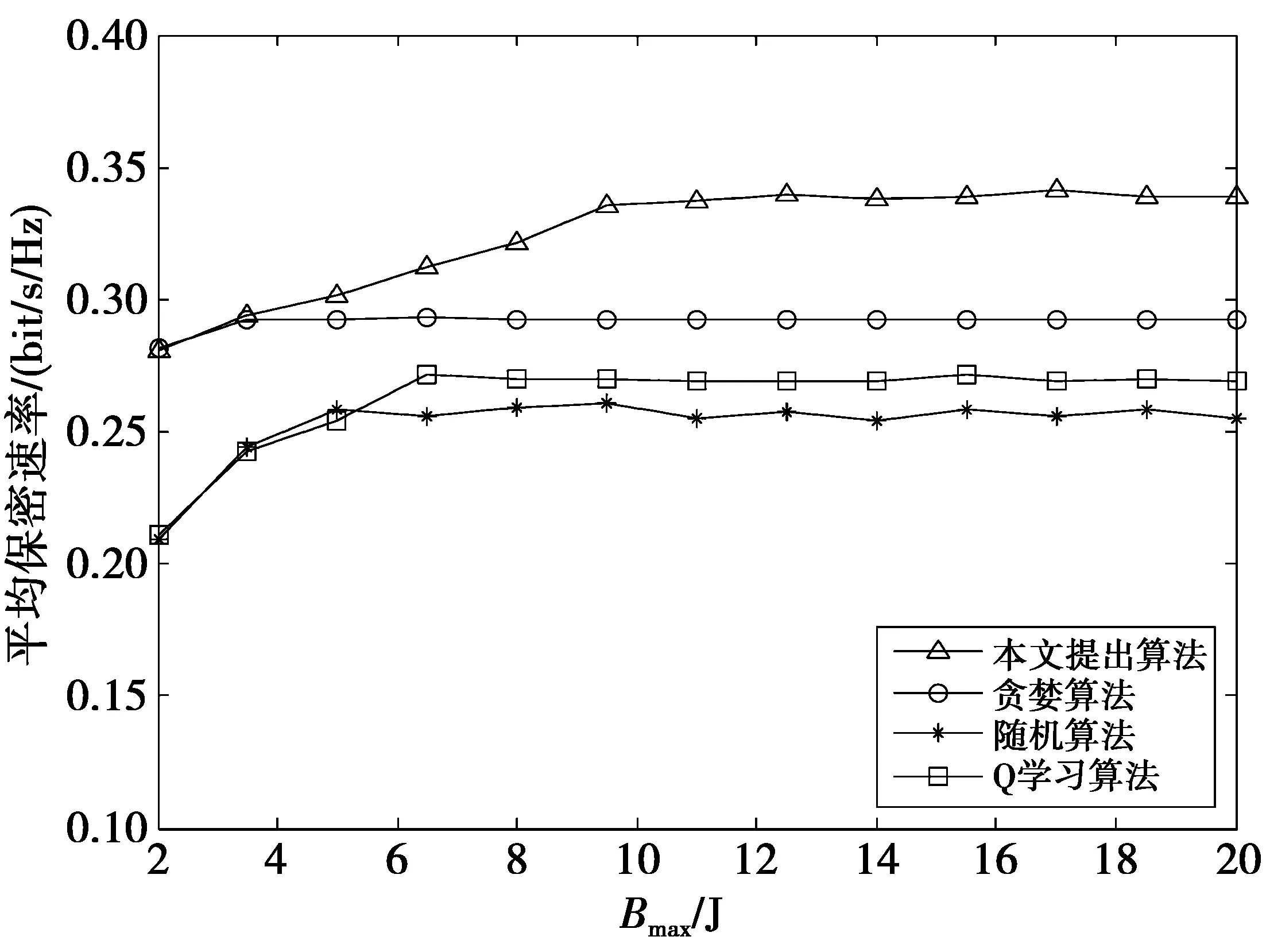
图5 Bmax对平均保密速率的影响Fig.5 Bmax impact on average secrecy rate

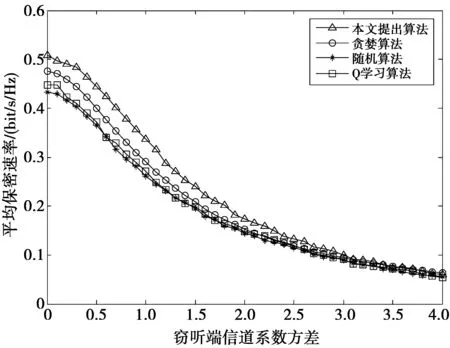
图6 窃听端信道增益对平均保密速率的影响Fig.6 Impact of eavesdropping channel gain on average secrecy rate

4 结束语

本文对能量收集和信道状态先验信息未知的条件下，能量收集窃听信道模型下最大化保密速率的功率控制问题进行研究，提出了一种基于DQN强化学习的在线功率分配算法。系统模型中包含发送节点、目的节点和窃听节点各一个。发送节点需要根据当前电池电量、收集的能量、合法信道和窃听信道的信道系数选择发送功率。为了提高能量的利用效率和信息的安全传输，将功率分配问题建模为MDP，用神经网络逼近值函数来解决传统Q学习算法无法处理连续状态空间的问题。仿真结果表明，本文提出的算法能够有效地提高系统的保密速率。