基于用户个性化需求的网络接入选择算法

马 彬，李江帆，谢显中

(1.重庆邮电大学 计算机科学与技术学院，重庆 400065；2.重庆邮电大学 重庆市计算机网络与通信技术重点实验室，重庆 400065)

0 引 言

随着社会的不断进步和通信技术的高速发展， 人类跨入无处不在的移动互联、互通时代、智能终 端、无线局域网、车联网、移动支付等一系列信息化技术给人们生活带来了更加优质便捷的体验。无线通信技术已经发展成为具有不同的带宽、调制方式和覆盖范围的异构无线网络[1]。

异构各种类型无线网络而成的异构无线网络，共同为用户提供无处不在的无缝漫游、透明的服务。然而每个用户对网络需求存在差异，导致网络接入选择算法在平衡网络服务质量和用户个性化需求方面，天然存在一些问题，这个问题也成为业界关注的热点问题之一。

当前提供用户个性化需求的网络接入选择方法中，可以按用户个性化需求的考虑程度划分为两类：一类从用户角度，获取对成本、吞吐量有需求的部分用户的偏好，根据偏好进行网络选择。文献[2]提出一种成本感知网络切换决策算法，使用户通过较低的成本获取低成本型网络服务；文献[3]通过非合作博弈的方法，研究其存在的均衡、收敛时间、效率和实用性，从而选出最佳接入网络，目的是最大化其自身的吞吐量；文献[4]以用户为中心，利用用户的偏好来调节模糊神经网络算法的规则，从而选取用户最合适的网络；另一类，考虑用户偏好的同时，也考虑一部分网络服务质量，进行适当的折中。文献[5]提出一种捕获用户偏好的分析模型，然后以用户偏好、服务质量、连接成本为参数，组成一个效用函数进行网络选择决策；文献[6]提出一种用于异构无线网络中的双向匹配算法，该算法分别以网络为中心和以用户为中心设立各自的评估模型，然后通过一对多双向匹配模型求得最优匹配解，从而得到最优网络选择；文献[7]提出的方法，考虑到用户偏好、网络状况、服务质量和能耗的要求，归一化后，构建效用函数，进行网络决策；文献[8]提出的方法，考虑了候选网络的用户偏好和异构网络的实际情况，结合了模糊层次分析法、熵值法和逼近理想解3种典型的多属性决策方法。

第一类仅考虑用户侧，没有考虑网络性能，导致效率太低；而第二类通过用户的偏好与网络的服务质量相结合的方法，时间复杂度高，权重的确定也有待商榷，且这类方法的用户偏好设置不够客观，不能表达用户的真实需求。上述研究虽然都考虑了用户的一些需求，但并未很好地刻画用户的个性化需求和满意度，而引入心理曲线函数和雷达图分析法，能更好表达用户满意度，从而在复杂度较低的同时，极大提高了算法的用户满意度。于是本文提出一种基于用户个性化需求的网络接入选择算法。该算法一方面基于模糊层次分析法得到用户对各网络属性的收益，引入了心理曲线函数，从而建立一个用户满意度模型；另一方面，考虑到更合理的表达用户对各网络属性的满意度综合值，本文结合改进的雷达图分析法，选取综合值最大的网络接入。本文的主要贡献总结如下。

1)引入心理曲线函数，考虑用户的期望收益和候选网络的当前收益，构建了一个更加客观的用户满意度模型；

2)引入基于生长曲线函数优化的雷达图分析法，构建一个最佳接入网络选择方法，在保证服务质量的同时，极大地满足了用户的个性化需求。

1 优化用户个性化需求的网络接入选择算法

首先，根据对现有研究工作的分析和本文对用户个性化需求的剖析，选取了价格、带宽、接收信号强度、负载率、误码率、阻塞率6个参数作为满意度模型的构建参数。并把上述参数划分为成本、系统性能、稳定性三大类评估属性，其中，价格属于成本属性，接收信号强度、带宽属于系统性能属性，误码率、阻塞率、负载率属于稳定性属性。其次，对上述6个参数进行归一化，使用模糊层次分析法，构建系统性能和稳定性两大类属性中，各参数的权重，根据历史数据和当前候选网络的实时数据，分别计算三大类属性的期望收益和当前收益，并引入心理曲线函数，进而构建一个用户满意度模型分别评价三大类属性的满意度；最后，引入基于生长曲线函数优化的雷达图分析法，来综合三大类属性的用户满意度，进而选择最大综合值的候选网络进行接入。网络接入选择过程如图1。

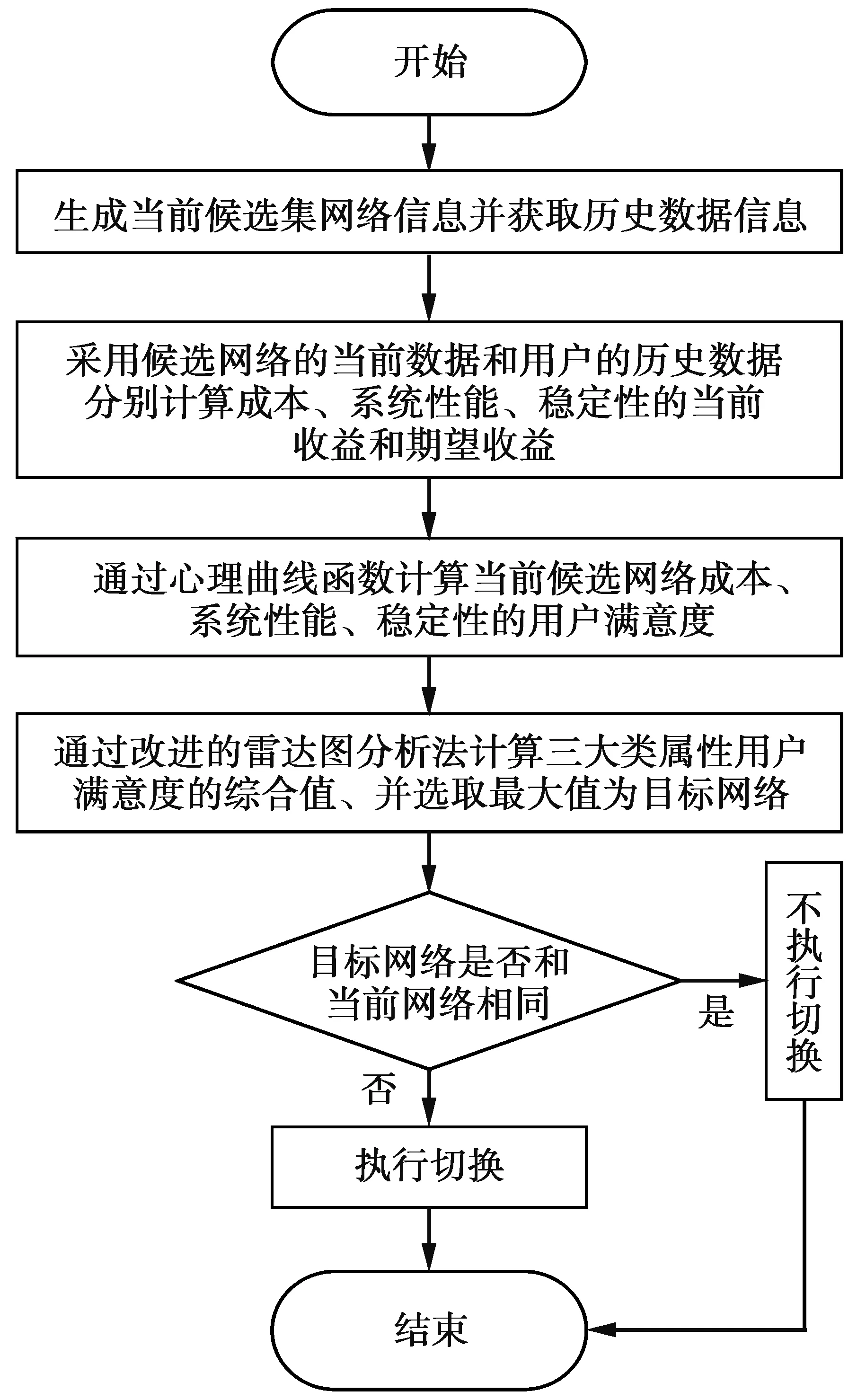
图1 网络接入选择过程Fig.1 Network access selection process

2 用户满意度模型

2.1 用户满意度的模型构建

用户满意度是对用户满足情况的评价，是产品与用户个性化需求匹配度的评价。对于本文而言，用户满意度是候选网络与用户个性化需求的匹配程度的描述。用户满意度是一个可变的动态目标。当前对用户满意度的刻画，有用户服务满足度法[2]、满意度函数(satisfaction degree function，SDF)法[9]等多种方法。本文为更好度量用户的满意程度，引入心理曲线函数[10]。心理曲线函数是基于用户的期望收益和当前收益，采用函数的方式对用户满意度进行刻画的一种定量方法，可表示为

(1)

(1)式中：β为用户满意度；α为期望收益；γ为当前收益。

本文基于心理曲线函数，提出了结合用户在三大类属性上的期望收益和当前收益，抽象出用户对候选网络集中网络的三大类属性的满意度模型。

1)成本满意度。

(2)

2)系统性能和稳定性满意度。

(3)

(2)—(3)式中：upc为成本pc的期望收益；oi,pc为第i个候选网络的成本pc的当前收益；ussi,pc为第i个候选网络的成本pc的满意度。

2.2 用户收益计算方法

本文涉及的收益包括2方面：①用户的期望收益，是通过用户的历史接入数据计算得出，包括历史情况中用户获取到各网络的成本、接收信号强度、带宽、误码率、阻塞率、负载率以及当时用户接入的网络信息；②当前收益，是用户可接入候选网络的实时采集数据计算得出。但是2种收益的计算过程均相同，本文重点分析用户当前收益的计算。

2.2.1 数据的归一化

为解决不同无线网络中各参数取值范围和单位的差异性，本文对上述6个参数分别进行归一化处理。而无线网络的参数可以分为效益型和成本型，其中，成本型属性越小越好，如价格、误码率、阻塞率、负载率；效益型属性越大越好，如接收信号强度、带宽。

1)成本型。

(4)

2)效益型。

(5)

对每个网络的6个参数归一化值分别进行排序可得集合

(6)

(6)式中，k表示为网络数量。

2.2.2 计算当前收益

系统性能属性由接收信号强度(received signal strength，RSS)、带宽B构成，稳定性属性由误码率D、阻塞率Z、负载率F构成。为了更准确地体现系统性能和稳定性的值，本文采用不同的权重来体现各参数在各属性中的重要程度。

大多数求取权重的多属性决策算法比较复杂，结果不够准确，无法描述参数的模糊性等不确定性，然而模糊层次分析法计算简单，采用该算法所得的权重能够更贴合地表达用户的个性化需求。于是本文引用模糊层次分析法[11]，分别计算接收信号强度、带宽在系统性能内的权重和误码率、阻塞率、负载率在稳定性内的权重。具体权重求取过程如下。

1)层次结构图构建。层次结构图如图2，将目标问题层次化，总的可以分为目标层、准则层以及方案层。目标层即为系统性能和稳定性的用户收益；准则层即为影响系统性能和稳定性的各判决因素；方案层即为各候选网络中各参数的归一化值。

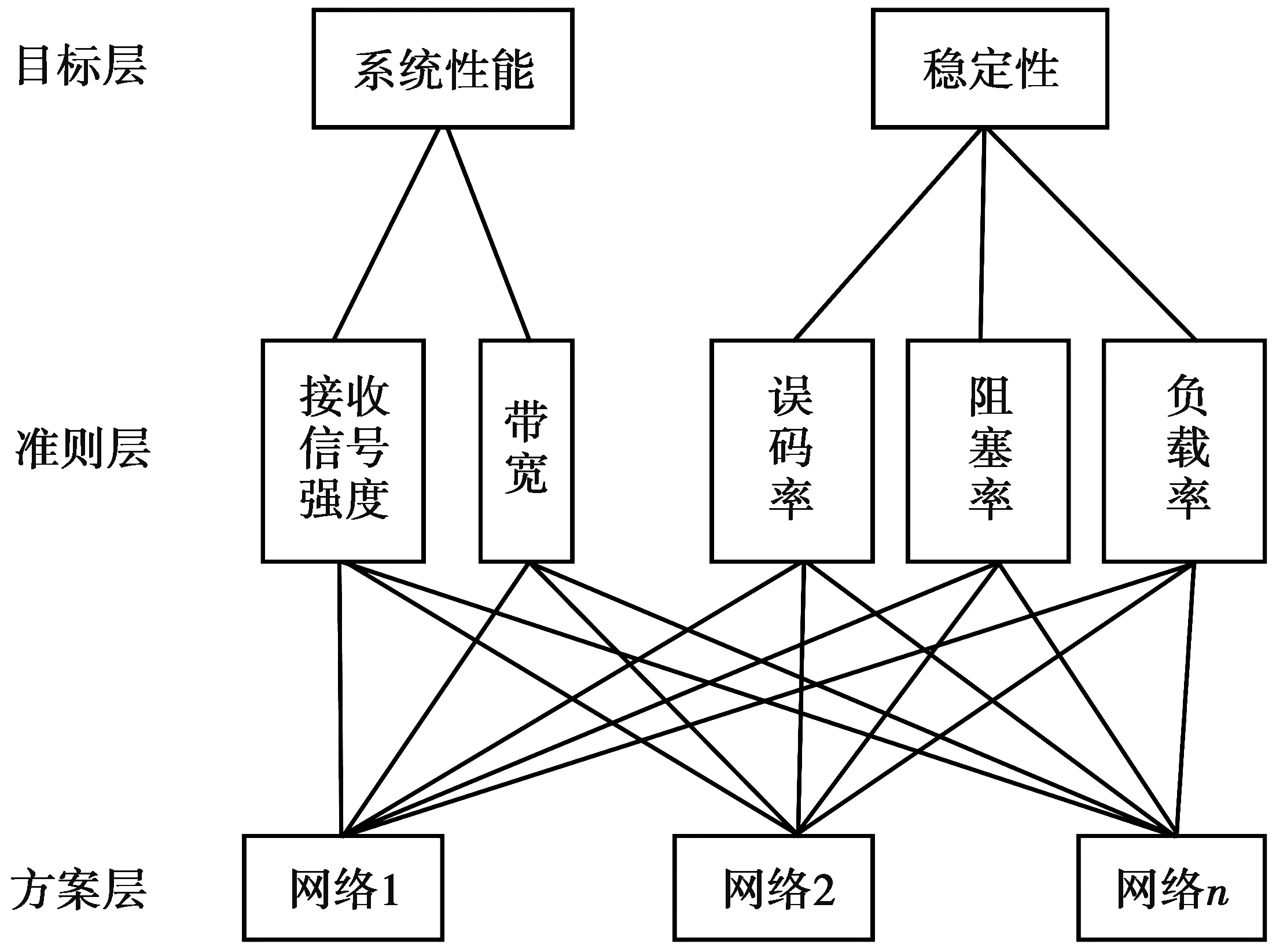
图2 层次结构图Fig.2 Hierarchy diagram

2)模糊互补判断矩阵。采用通用的模糊判断矩阵计算方法，将准则层中的5个参数分成2个组，分别构建矩阵表达对目标层中系统性能和稳定性的重要性。通过两大属性各自参数间两两比较，分析得到定量的标度值rab(rab表示第a行第b列的数值)，从而分别得到模糊互补判断矩阵R=(rab)n×n，代入两大属性得到相对应的系统性能和稳定性的模糊互补判断矩Rsp和Rst，其中，rab的具体取值方法为0.1～0.9标度法，如表1。

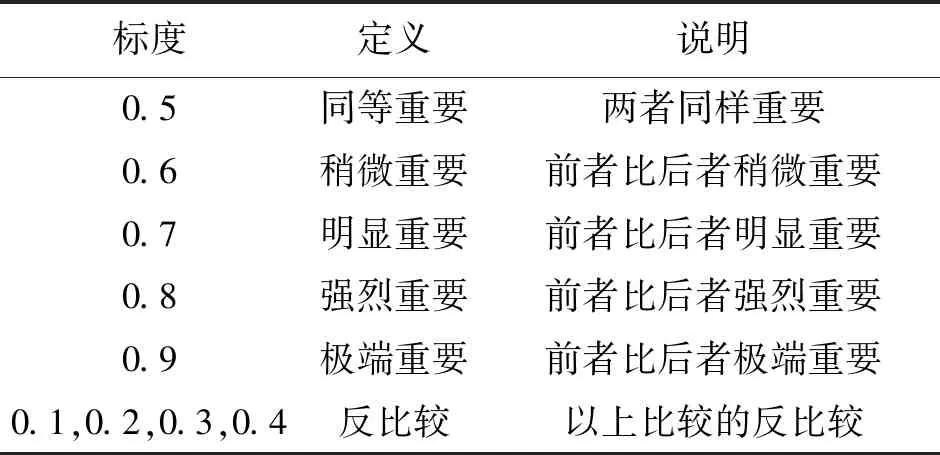
表1 0.1～0.9标度法Tab.1 0.1～0.9 scale method

本文根据以上标度法获得的Rsp和Rst分别表示为

RSSB

(7)

DZF

(8)

3)权向量计算。本文使用求解模糊互补判断矩阵权重的通用公式得到各参数权重，表示为

(9)

把矩阵(7)，(8)式分别代入(9)式求得系统性能和稳定性的权重向量分别为

RSSB

(10)

DZF

(11)

(10)—(11)式中：wsp为系统性能sp的权重向量；wst为稳定性st的权重向量。因此，系统性能sp中RSS，B的权重分别为0.45，0.55。稳定性st中D，Z，F的权重分别为0.434，0.358，0.208。

4)模糊矩阵R=(rab)n×n的一致性检验。由(9)式得到的权重值是否合理,还应该进行比较判断的一致性检验。为验证模糊矩阵R=(rab)n×n的一致性，首先构建矩阵R的特征矩阵W*=(wab)n×n，即W*为wab的n行n列矩阵，其中wab为

(12)

(12)式中，wab表示第a行第b列的权重。

本文用模糊判断矩阵的相容性来检验其一致性原则的方法。当偏移一致性过大时，表明此时将权向量的计算结果作为决策依据是不可靠的。矩阵的相容性为

(13)

如果相容性值I(R,W*)≤T，那么认定一致性符合标准，否则需要对矩阵R=(rab)n×n进行调整，重新求权，通常设定相容性指标临界值T=0.1。

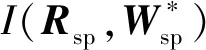
(14)

(15)

由此可知，系统性能和稳定性的模糊判决矩阵都具有一致性，权重值结果完全合理。

(16)

(17)

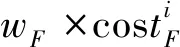
(18)

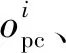
2.2.3 期望收益的获取

设从历史数据中得到用户j在面临m次网络重叠时，m组参数数据及用户选择网络的结果。m组数据代入2.2.2节公式，得到用户j在历史数据中，m组用户选择网络的成本、系统性能、稳定性的综合值集合，即

(19)

(19)式中，q分别为三大属性。但是历史数据中m次重叠网络下用户选择各属性的数值可能有少部分数据失真，于是本文把h次重叠网络情况得到的各属性综合值求平均值，即

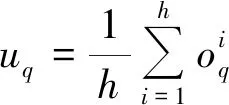
(20)

3 基于改进雷达图分析法的网络寻优

3.1 基于改进雷达图分析法的网络寻优

为了综合评估用户的满意度，本文引入雷达图分析法。雷达图分析法是为得到综合价值评估的一种评价方法。封闭图形的面积是各信息的一个多元函数，因此，面积可以体现多元数据的综合特征。面积愈大，表示该评价对象的总体优势愈大，其竞争力就愈强；面积愈小，表示其总体优势愈小，竞争力也就愈弱。

一个正七边的七阶雷达图如图3，从圆心出发，画射线1～7为评价指标，浅色正七边形网表示可视化刻度线，射线上的数值表示归一化的各项指标的刻度值，数值为[0，100]。不规则七边形的面积与各指标数值最大时所围成正七边形面积的比值，表示为综合价值。

图3 七阶雷达图Fig.3 Seventh-order radar diagram

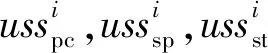
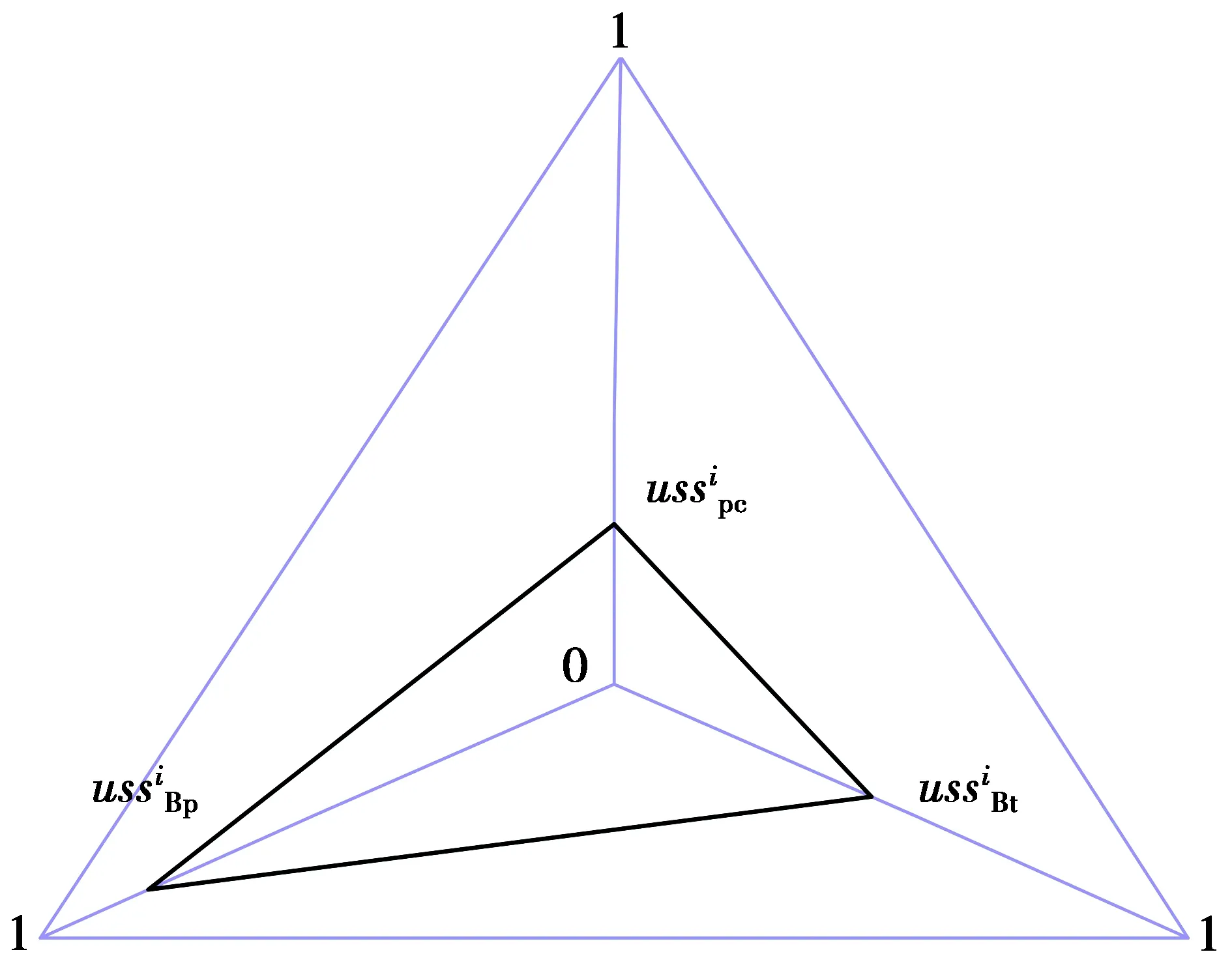
图4 满意度雷达图Fig.4 Radar diagram of satisfaction

由于成本、系统性能、稳定性满意度的实际数值所围成的三角形面积，随着各属性满意度值的增加，呈先慢后快的递增曲线A，在一般的多评价指标线性增长情况下，综合值也是线性增长，而在本文中，因为三角形的面积为指数增长，所以综合满意度呈先慢后快的增长趋势，不能准确表达结果。为了保证综合满意度增长的公平性，需保证综合满意度呈线性增长，即曲线函数M，于是本文引入生长曲线函数N。在使用雷达图分析法运算后，再把得到的结果代入生长曲线函数从而得到线性增长的综合值，即总满意度。函数曲线见图5。

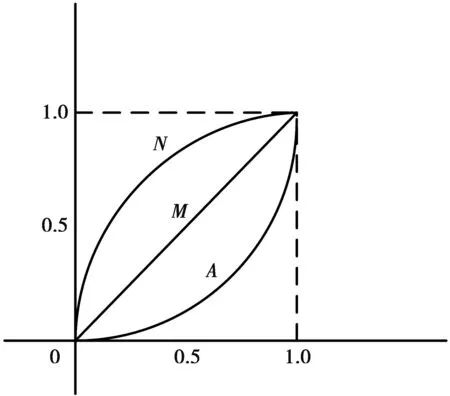
图5 函数曲线图Fig.5 Curve of the function

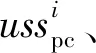
(21)

(21)式中，ω1是正三角形的中心角，ω1=120°，为了保证公平性，本文引入生长曲线函数的通用公式，对面积S1进行面积线性增长的处理，得到线性处理后的面积为

S2=g×ab×S1+e

(22)

(22)式中：g=1；a=-0.01；b=1；e=1。

最大正三角形的面积为

(23)

(23)式中：ω2为正三角形的内角，ω2=60°；r为最大正三角形的边长。

于是，面积S2和总面积Sz的比值为

(24)

(24)式中，ossi表示用户对候选网络i的总满意度。

3.2 最优网络选择

本文通过历史数据获得用户对成本、系统性能、稳定性的期望收益，并通过对当前候选网络的数据计算，获得候选网络成本、系统性能、稳定性的当前收益。代入用户满意度模型中，可获得用户j对第i个候选网络的总满意度集合OSSj，选取用户j的候选网络集合中满意度最大的网络接入。总满意度集合表示为

(25)

(25)式中，m为候选网络数量。

由于历史数据中每个用户对成本、系统性能、稳定性的期望收益不同，本算法选择候选网络中每个用户最满意的网络，以满足用户的个性化需求。

4 实验结果及分析

4.1 仿真环境及参数设置

实验仿真环境由m个无线网络和k个终端用户构成。本文构建了一个异构无线网络仿真场景，其中包含1个4G网络，2个WiMAX网络，3个WLAN网络，如图6。各网络的网络覆盖半径分别为11，5，1 km，网络与用户的位置通过一个二维坐标(x，y)给出，其中，E为坐标原点，射线EG为x轴，4G网络的基站坐标分别位于[75,75]；WiMAX网络的基站坐标WiMAX1为[55,75]，WiMAX2为[95,65]；WLAN网络的基站坐标WLAN1为[70,65]，WLAN2为[82,62]，WLAN3为[77,56]。

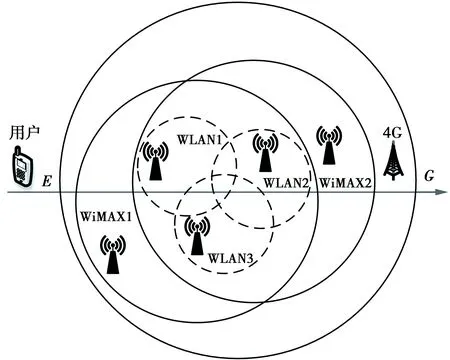
图6 异构无线网络系统模型Fig.6 Heterogeneous wireless network system model

假设用户终端皆从E(0,60)点出发，以最大速度5 m/s移动至G(150,60)点。干扰接收信号强度服从VM(x)=-130+ε(x) dBm，ε(x)服从参数为(0,10)的高斯随机分布。各网络的仿真参数设置如表2，异构无线网络系统模型见图6。

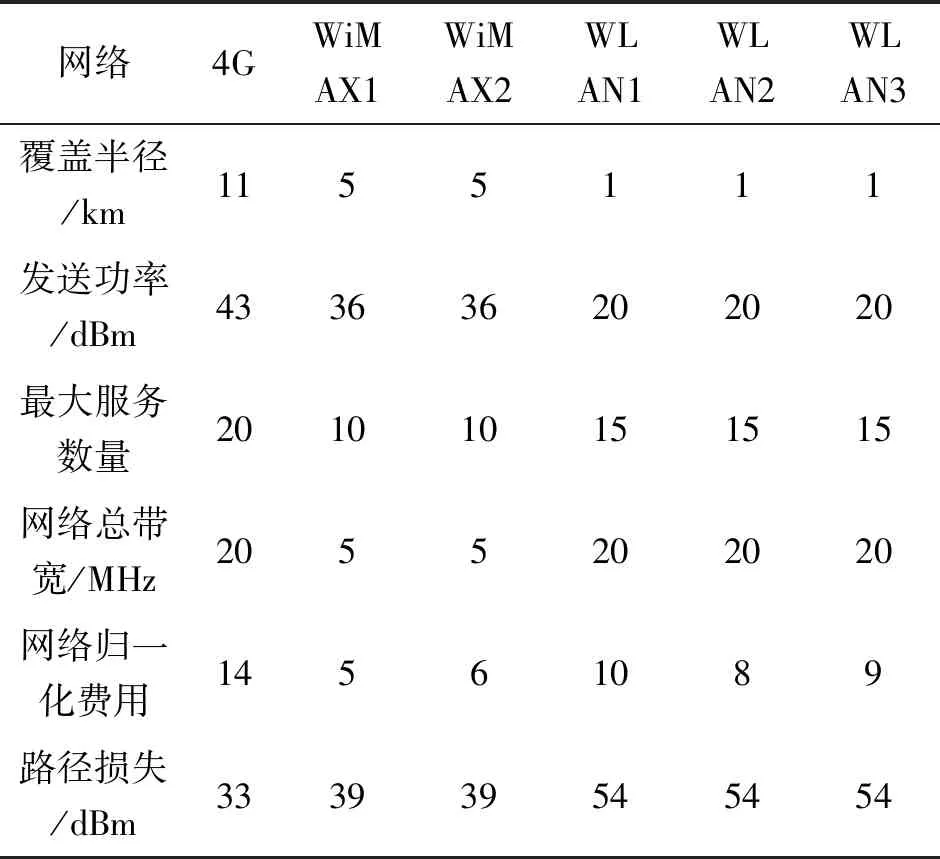
表2 网络仿真参数设置Tab.2 Network simulation parameter settings

实验中对比了本文的基于用户个性化需求的网络选择接入算法(network access selection algorithm based on user requirements，UR-NAS)分别与基于模糊层次分析法的网络选择接入算法[12](utility based non-linear fuzzy AHP optimization model for network selection in heterogeneous wireless networks，FAHP-NAS)和基于效用函数的网络选择接入算法[13](joint multi-criteria utility-based network selection approach for vehicle-to-infrastructure networking， Utility-NAS)。本文分别从用户满意度、用户切换情况和负载率3个维度，设计了3组实验，分析了本文算法的综合性能。通过实验仿真证明，满足了用户个性化需求，在保证了系统负载均衡的同时，降低了乒乓效应。

4.2 用户满意度分析

平均用户满意度对比如图7,可以看出，3个算法的平均用户满意度曲线变化规律基本一致，3个算法均在用户数小于10时出现大幅的波动，其余随着用户数的增加曲线基本持平，最后，本文算法和FAHP-NAS算法的曲线趋于重合，但本文所提算法相较另外2个算法的满意度均要略高一些。

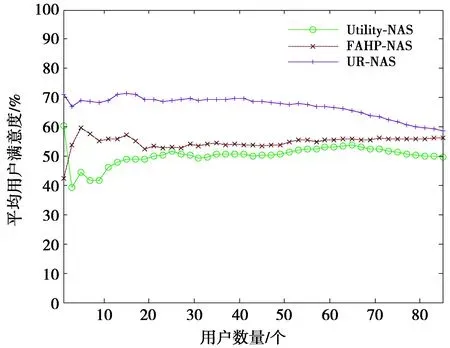
图7 平均用户满意度对比Fig.7 Comparison of average user satisfaction

用户数小于10时，历史样本数据太少，导致对用户期望收益的计算存在很大的不确定性，从而导致满意度不稳定，但是随着用户数的增加，满意度趋于稳定；Utility-NAS和FAHP-NAS算法更多的是考虑网络性能，造成选择网络的结果比较接近，用户满意度也就比较接近，所以在用户增加的过程中出现多次重合；本文算法和FAHP-NAS算法在最后用户饱和的时候，由于避开了负载较高的网络，对网络选择的结果趋于一致，导致用户满意度趋于重合。本文的UR-NAS算法在3种算法中平均用户满意度最高，这是由于本文的算法不但保证了网络服务质量，而且还满足了用户个性化需求，从而提高了用户满意度。该仿真结果说明本文提出的算法更能满足用户的个性化需求。

4.3 切换次数和乒乓效应分析

平均切换次数对比如图8，分别采用不同的算法实验仿真50次，平均每个用户的切换次数，在FAHP-NAS算法下切换了10.82次，在Utility-NAS算法下是8.40次，而本文提出的UR-NAS算法是6.20次。在仿真中，每次仿真时用户的需求值设定是不同的，导致一部分情况下各算法的平均切换次数相同，但是在大部分情况下，FAHP-NAS算法的平均切换次数比Utility-NAS和UR-NAS算法高，而UR-NAS算法的平均切换次数最低，Utility-NAS算法的平均切换次数则趋于两者之间。

图8 平均切换次数对比Fig.8 Comparison of average switching times

图9显示随着用户在仿真场景中的移动，累计切换次数的变化，图9中，在仿真场景5 000 m之前，FAHP-NAS算法和Utility-NAS算法累计切换次数相同，都增加了1次，本文的UR-NAS算法增加了0次，但是在5 000～10 000 m，UR-NAS算法增加了2次，而FAHP-NAS算法增加了11次，Utility-NAS算法增加了7次，10 000 m之后，没有发生变化。这是由于在5 000～10 000 m中，网络场景复杂，本文提出的UR-NAS算法是选取满足用户个性化需求的网络即可，而FAHP-NAS算法和Utility-NAS算法一旦遇到比接入网络更好的其他网络，就会选择立马切换，所以本文的UR-NAS算法切换次数相对于FAHP-NAS算法和Utility-NAS算法较少。这一现象充分说明本文提出的算法有效地降低了用户不必要的切换次数。

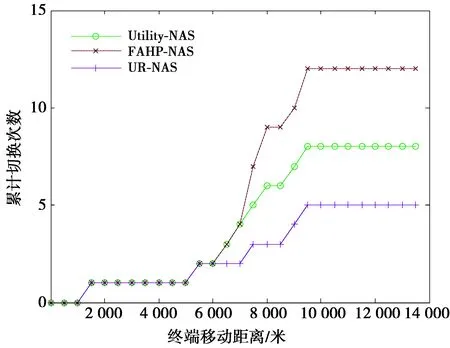
图9 累计切换次数对比Fig.9 Comparison of cumulative switching times

图10显示3种算法随着仿真次数的增加，乒乓切换率的对比，乒乓切换率是用户在相邻小区之间短时间发生切换的次数与运动过程中的总切换次数的比值。可看出在50次的仿真中，Utility-NAS算法的平均乒乓切换率为17%，FAHP-NAS算法的平均乒乓切换率为6%，而本文提出的UR-NAS算法的平均乒乓切换率为2%。由于用户个性化需求在每次仿真中都是不同的，所以少数情况下各算法的乒乓切换率相同，但是在大部分情况下，本文算法乒乓切换率最低，FAHP-NAS算法次之，Utility-NAS算法最高。这是由于本文UR-NAS算法的思想是网络能够满足用户的最低要求即可，不会出现当另外一个网络比接入网络稍好就立即进行切换，通过仿真结果，说明本文提出的UR-NAS算法有效降低了乒乓效应。

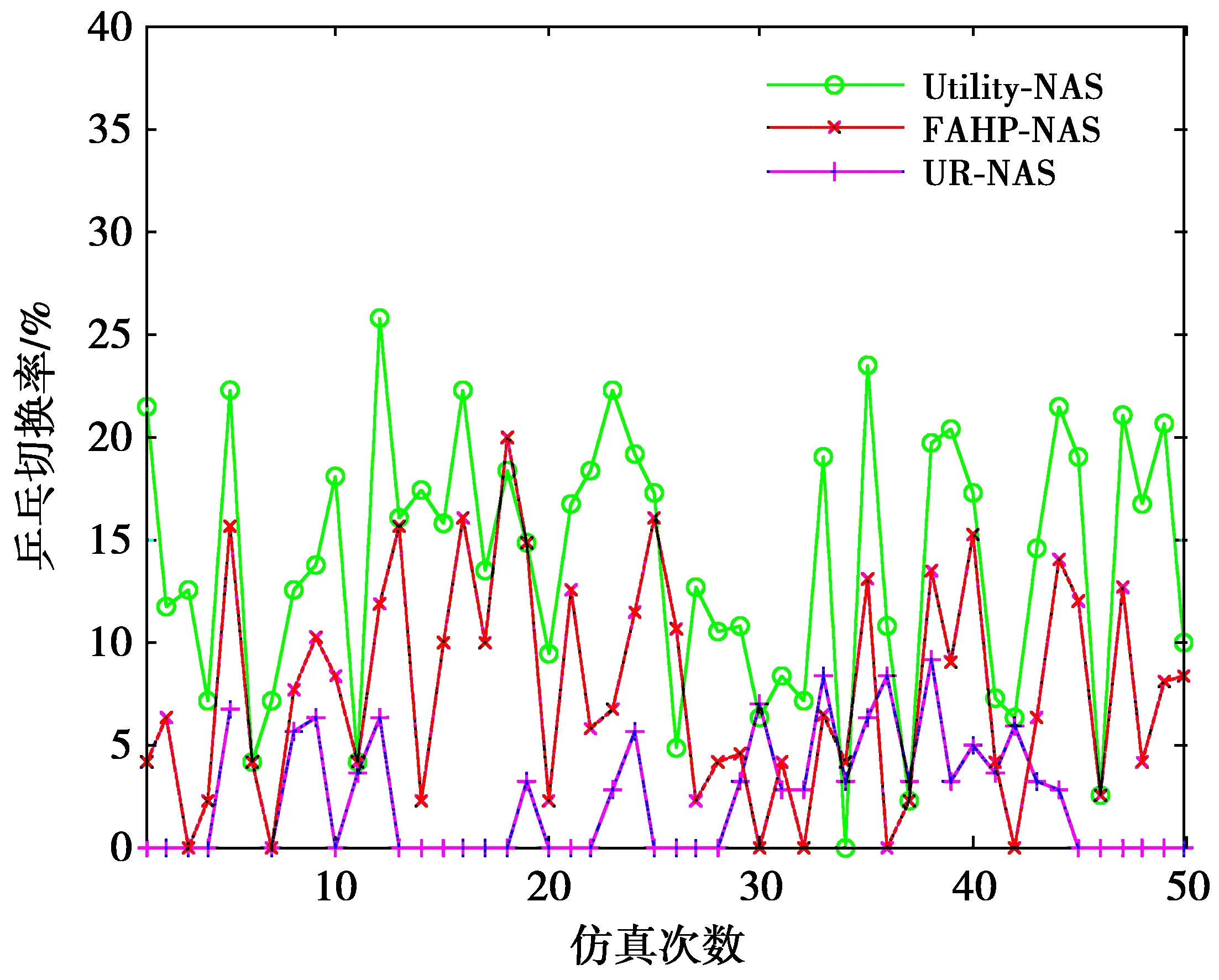
图10 乒乓切换率对比Fig.10 Comparison of ping-pong switching rate

4.4 负载率分析

图11对比了在用户数量增多的趋势下，3种算法的平均负载率，平均负载率是描述当前用户连接数量与各网络可连接总用户数量的平均比值。可以看到，随着用户数量的增加，3种算法的平均负载率不断增加，直到达到网络负载极限时，负载率达到100%。从图11可知，在用户数量达到30之前，UR-NAS算法、FAHP-NAS算法的平均负载率基本一致，Utility-NAS算法平均负载率略低，在用户数量个数从30增加到65时，UR-NAS算法的平均负载率略高于FAHP-NAS算法和Utility-NAS算法，这是由于在候选网络较多时，本文算法选取网络的标准为满足用户个性化需求的网络，从而导致平均负载较高；用户数量从65增加到85时，UR-NAS算法、Utility-NAS算法的平均负载率基本一致，FAHP-NAS算法的平均负载率略低。UR-NAS算法、FAHP-NAS算法和Utility-NAS算法的平均负载率在用户的增加过程中波动很小，说明UR-NAS算法的负载均衡程度和其他2种算法基本相同，即UR-NAS算法达到了负载均衡。

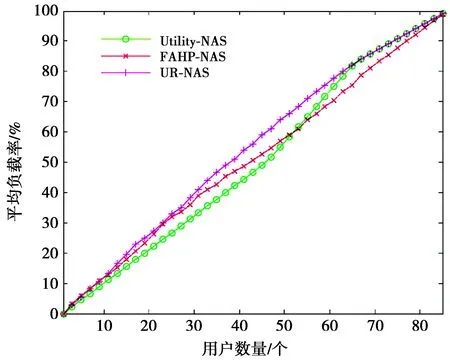
图11 平均负载率对比Fig.11 Comparison of average load rate

5 总 结

本文提出了一种基于用户个性化需求的网络接入选择算法。在文中设定一种用户满意度模型来评价用户对通过算法选择出来的各网络属性的满意程度，然后通过基于生长曲线函数优化的雷达图分析法来得到候选网络满意度的综合值。仿真实验结果表明，本文提出的算法及用户满意度模型满足了用户的个性化需求，提高了网络服务质量，在保证了负载均衡的同时，有效地降低了乒乓效应。