基于聚类的PCA和GRNN的CSI指纹定位算法
李新春,黄朝晖
(1.辽宁工程技术大学 电子与信息工程学院,辽宁 葫芦岛 125105;2.辽宁工程技术大学 研究生院,辽宁 葫芦岛 125105)
0 引 言
便携设备的发展在当前新兴领域的增长中扮演着重要的角色,如基于位置服务(location based services,LBS)[1]和物联网应用(Internet of things applications,IOTA)[2-3]。在室外场景下,全球定位系统(global positioning system,GPS)基本满足了LBS和IOTA的需求,而室内环境中尚无法满足。于是基于无线局域网(wireless local area network,WLAN)的室内定位技术由于具有设备简单、覆盖范围广、普适性强等特点从中脱颖而出[4]。
目前,大多基于WLAN的定位方案使用接收信号强度(received signal strength,RSS)作为位置指纹[1-2,5]。然而,复杂室内环境中RSS的稳定性和可靠性受到多径衰落和时间动态的制约[6],若将其作为信号特征并应用于定位中,则需大量的接入点 (access point,AP)以及复杂的数据处理工作来避免误匹配的问题。相比之下,作为物理层的细粒度信息的信道状态信息 (channel state information,CSI)可以表征该位置的多径特性,体现在对噪声干扰的强大鲁棒性上,因而选择CSI作参量的定位方法在定位精度上大多优于RSS。
文献[7]结合CSI频率和空间上的数值并求其均值代替RSS作为指纹,验证了定位精度优于传统的RSS识别方法。文献[8]利用多输入多输出(multiple-input multiple-out-put,MIMO)技术对多载波多天线的CSI进行聚合,并分别使用K近邻和概率贝叶斯得到目标位置的估计值。以上2种方法均使用所有样本的平均值,而均值方法并不能充分地反映出位置的多径信息。文献[9]将深度学习应用于CSI指纹训练,提出了DeepFi系统,利用贪心算法训练多重数据包以重构指纹,通过径向基函数(radial basis function,RBF)的概率方法估计位置,其中利用反向传播算法对权值微调,很容易陷入局部最优,多次训练会影响收敛速度。文献[10]提出一种基于支持向量机(support vector machine,SVM)的位置预测法,该方法使用DBSCAN(density-based spatial clustering of applications with noise)对CSI数据进行去噪,并利用主成分分析(principal component analysis,PCA)提取数据的主值特征以减少维数,建立指纹与位置间的非线性映射,虽然PCA解决了数据的维度问题,但SVM对于大规模的训练样本有着一定的局限性。文献[11]利用奇异值分解(singular value decomposition,SVD)融合子信道信息以获取指纹识别的主要成分,并分析指纹位置的几何特征,通过K最近邻和投票机制实现最终定位。然而,以上算法大都仅依赖CSI的幅值参量,却很少采用相位信息,因而在定位精度上仍有很大的提升空间。
本文针对上述基于CSI定位方法中存在的问题,提出了一种基于聚类的PCA和广义回归神经网络(generalized regression neural network,GRNN)的CSI指纹定位算法。该算法将修正后的CSI幅值和相位作为联合指纹,通过改进的K-means算法对每个参考点的联合指纹集进行聚类,并将各个类的中心作为联合指纹的子数据集,然后利用高维数据的PCA算法对子数据集进行特征提取以降低子数据信息的冗余度,最后利用广义回归神经网络模型实现位置预测,平衡定位的准确性与适应性。
1 信道状态信息
1.1 CSI介绍
CSI是通信链路间信道属性的估计值,利用正交频分复用(orthogonal frequency division multiplexing,OFDM)技术可将收发链路间子载波级的CSI提取出来。作为细粒度表征的CSI,囊括了信号经历各种传播方式带来的干扰和衰减等信息[12]。对于802.11n标准[13]下的OFDM系统,在频域内的信道响应可表示为
Y=HX+W
(1)
(1)式中:Y,X分别为接收和发射的信号序列;H为信道矩阵,包含了CSI的幅值和相位信息;W为随机噪声。
OFDM系统在20 MHz带宽信道下可以提供56 个子载波,而利用装有Intel 5300 NIC的设备可以从一些商用网卡中获取出30个子载波[13],由此组成的CSI矩阵H,可表示为
H=[H1,H2,…,HN]
(2)
(2)式中,每个子载波Hi被定义为
Hi=|Hi|ejsin(∠Hi)
(3)
(3)式中,|Hi|和∠Hi分别为第i个子载波的幅值和相位,其中,i∈[1,2,…,N],N=30。
1.2 预处理
CSI数据以复数形式存在,具有幅值和相位2个参量。幅值参量由于直观规律性强、便于计算而被广泛使用,而相位参量因受频偏影响有着明显的相位跳变或偏移[14],这将导致测量的相位值无法直接作为定位的指纹特征。因此,为了充分地利用CSI所携带的信息,以确保建立的定位模型的准确性,从而满足更稳定和更高精度的定位需求,需分别对原始信息中的幅值参量和相位参量进行预处理,并将其作为原始联合定位的指纹特征。
1.2.1 幅值的处理
室内场景中,多径传播影响着CSI幅值的波动,而在传播过程中,一些不可控的因素会导致波动偏离正常范围而产生异常值。根据拉依达准则检测异常值,如果波动的偏差超过3倍标准差,则认为异常存在。若直接剔除异常值,会导致数据缺失,影响定位算法的性能,因而文中利用中值来替代。图1给出了CSI幅值滤波前后的波形对比图,其中,图1a为滤波前,图1b为滤波后。从图1可看出,原始的幅值波形图存有明显的异常值,而加入滤波之后,异常值被有效地处理了。
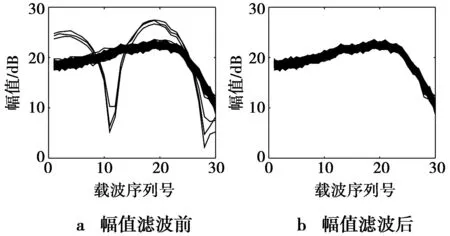
图1 幅值滤波前后的波形图Fig.1 Comparison before and after amplitude filtering
1.2.2 相位处理
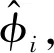
(4)
(4)式中:i∈[1,2,…,N],N=30;ki表示第i个子载波的编号(子载波编号的具体数值可查阅文献[13]),ki∈[-28,-26,…,-2,-1,1,3,5,…,27,28];Nfft是FFT的采样数;δ是定时偏移;β是未知的相位偏移;Z是测量噪声。
显然,由于未知的δ,β会导致相位的跳变和随机偏移。为减少随机噪声的影响,利用线性变换[13]移除δ,β以校准原始相位,并将校准相位作为指纹定位的指标。图2描述了原始相位测量值和转换后的校准相位。分别定义相位的斜率a和整个频段的偏移量b(忽略小的测量噪声Z)分别为
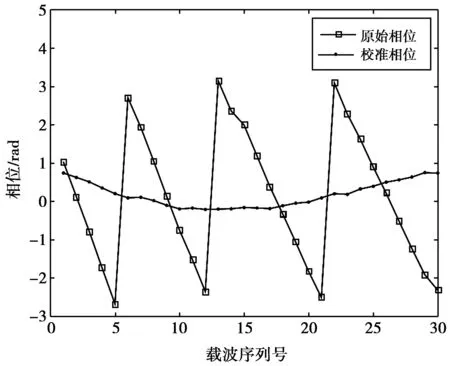
图2 相位线性变换处理Fig.2 Phase linear transformation processing
(5)
(6)
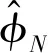
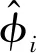
(7)
2 基于聚类的PCA算法
本文利用一台路由器作为AP(2天线),一台装有Intel 5300 NIC(3天线)的笔记本电脑作为接收终端,通过CSI Tool[15]可以获取CSI数据,利用Linux的系统函数可将其导出为.dat文件形式。考虑到采样次数n,AP发射天线数TX,NIC接收天线数RX和子载波数N,在某参考点处采集到的CSI数据是一个n×TX×RX×N的数值矩阵。
而n次采样的数据为选取位置指纹带来2个突出问题:①由于无线信号的多径传播影响着CSI值成簇分布的情况[9,16],若仅求n次采样的均值,则弱化了CSI数据所携带的信息,从而影响算法的定位精度;②CSI作为高维度的数值矩阵,意味着需要处理更多的信息,既降低了算法的定位精度又增加了算法的时间开销。因此,从多径影响下的CSI数据中选出用来描述位置多径特性的指纹数据以及降低数据维度是提高定位准确度、减少算法时间开销的关键所在。本文提出利用改进的K-mans算法将原始指纹集划成多个子数据集以便更好地反映位置的多径特性,再利用高维数据的PCA算法提取特征以降维,将特征指纹用于后续定位。
2.1 改进的K-mans算法
K-mans聚类算法[17]是一种经典的无监督学习方法,利用迭代思想将数据集划分为不同的类,从原理可知,初始聚类中心是随机选择的。在本文中,如果随机选取的K个中心具有强相关性,则易陷入局部最小解,甚至聚类结果出现错误[18]。为避免强相关性,在几个数据密集区的中心选取初始的聚类中心,可以加快周围数据的归类,也提高收敛速度。本文利用n次采样的CSI数据的均值μ和标准差σ来选取初始的聚类中心。
离线阶段,在某参考点处收集n个CSI数据包并进行预处理,将修正后的幅值和相位参量相结合,作为原始联合指纹集Raw,其形式为
Raw=[AP]
(8)
(8)式中,A和P分别为CSI的幅值矩阵和相位矩阵,包括所有TX-RX链路的所有子载波的幅值和相位信息。
假设聚类数为K,选择(μ-σ,μ+σ)的K个等分点进行分类,设第j类的初始聚类中心为Cj,则有
(9)
聚类算法流程如下。
1)依据(9)式从n组原始指纹集中选择K个初始聚类中心;
2)计算每个指纹对象与K个中心间的欧式距离,并按照平方和最小原则划分每个对象;
3)操作完所有指纹后,计算各个类的均值作为新类的中心;
4)循环执行2)—3)过程,直到聚类中心不再改变;
5)输出K个聚类中心。
聚类结束后,从n组原始指纹集Raw中得到K个具有代表性的子数据集,包含幅值和相位。输出的K个聚类中心所组成的子数据集C为
C=[C1,C2,…,CK]T
(10)
(10)式中,CK=[AKPK]为第K个类的聚类中心。
由于原始指纹集Raw是一个n×D的数值矩阵,其中,D=TX×RX×N×2,而“2”代表幅值和相位2个参量。通过聚类算法将原始指纹集Raw划分成K个子数据集C,即C为K×D维数值矩阵。换言之,聚类算法减少了每个参考点的数据量。然而维度仍然很高,高维数据的处理既影响定位精度也增加执行时间。为解决数据的维度问题,将通过高维数据的PCA算法来提取子数据集的特征,实现由高维向低维的转变,以减少定位算法的执行时间。
2.2 高维数据的PCA算法
PCA是一种被广泛应用在维度降低、数据可视化、数据压缩等领域的技术。PCA算法主要使用最大方差理论将高维数据映射到相互正交的低维空间。本文中,通过改进的K-means算法减少了参考点的数据量,会导致指纹的数据量小于指纹的特征维度。若直接使用PCA提取特征,则会发现大部分特征值均为零[19],在计算上是不可行的。为解决这一问题,做如下处理。
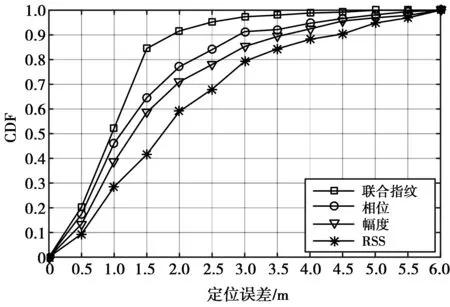
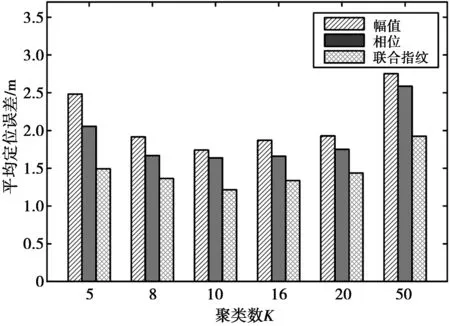
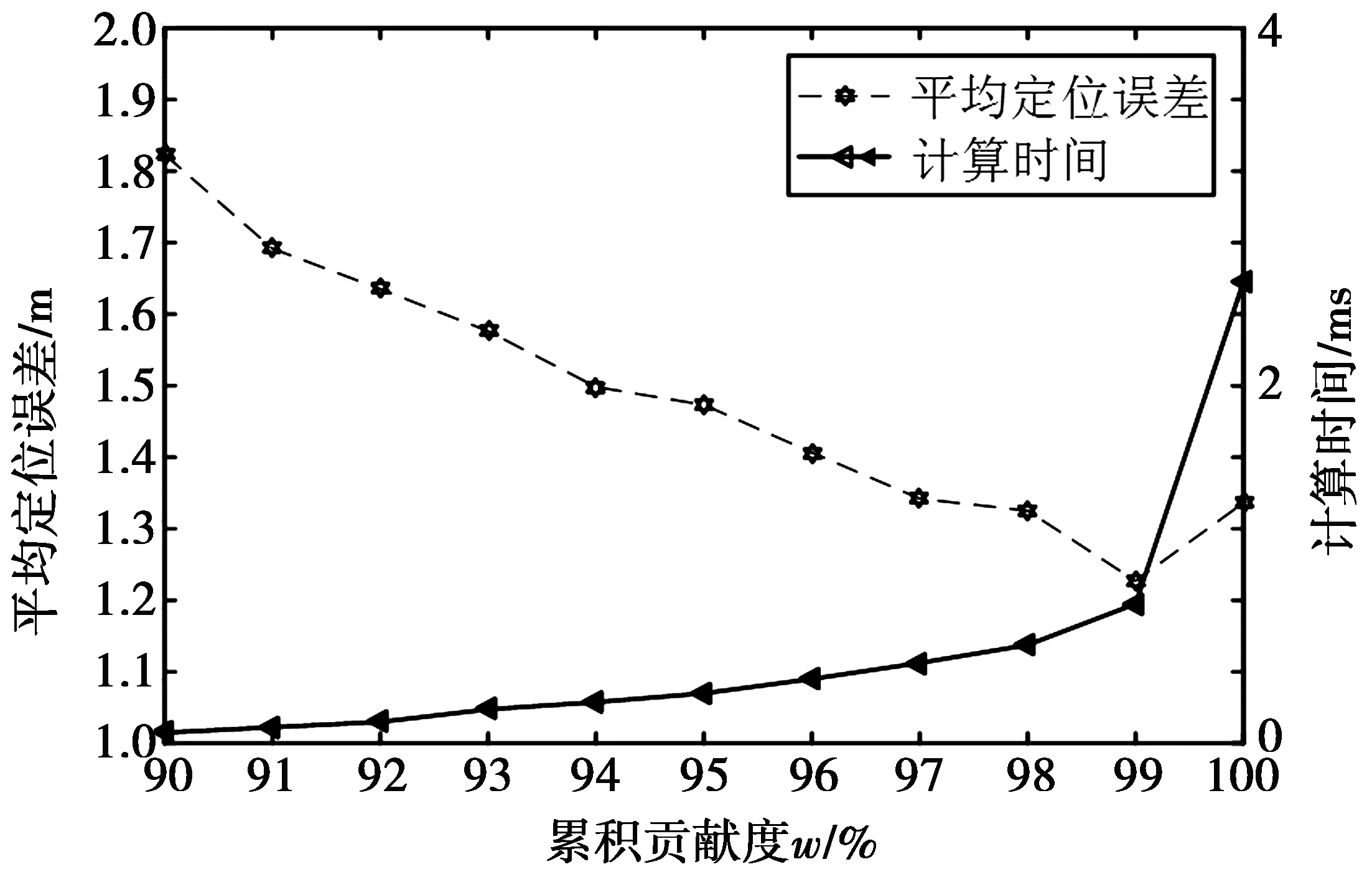
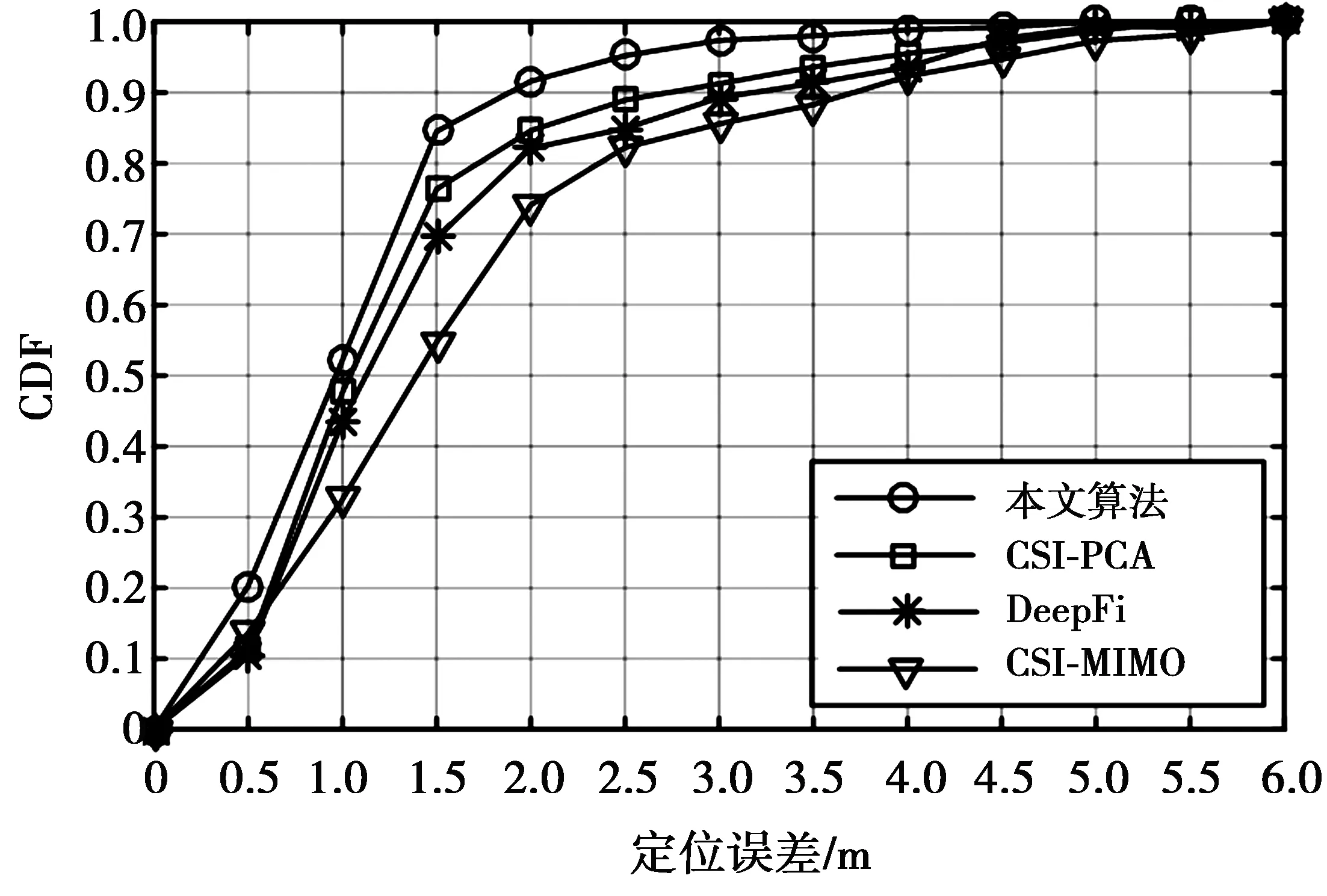
经聚类算法训练后的子数据集C为一个K×D且K (11) 在(11)式的两侧同时左乘X,可得 (12) 若定义vi=Xui,并代入(12)式中,则有 (13) (13)式是K×K维矩阵K-1XXT的一个特征向量方程。观察并发现K-1XXT与K-1XTX之间有K-1个相同的特征值,而K-1XTX至少有D-K+1个值为零的特征值,因此,我们可在低维空间中解决特征向量的问题。为确定特征向量,在(13)式的两端同左乘XT,可得 (14) 观察(14)式,可发现(XTvi)为S的一个特征向量,且与特征值λi相对应。为使投影方差最大化,需要满足归一化条件‖ui‖=1,因而需重新标度ui∝XTvi。假设已对vi做了归一化处理,那么就有 (15) 利用高维数据的PCA算法提取主特征值,具体步骤如下。 输入:聚类中心矩阵C(K×D)。 输出:前q个主特征值[λ1,λ2,…,λq]。 2)根据(13)式计算协方差矩阵K-1XXT的特征值λi和特征向量vi; 3)利用(15)式算出原空间的特征向量ui; 5)输出前q个主特征值,从大到小依次为[λ1,λ2,…,λq],并将其视为指纹信息作为广义回归神经网络的输入值。 设定位区域内有m个参考点,在每个参考点处采样n次,则参考点i处的原始指纹信息为Ri=(Rawi1,Rawi2,…,Rawin),与其相对应的位置坐标为Li=(xi,yi),经聚类的PCA算法处理后,构成该点的特征位置指纹Fi=(λi1,λi2,…,λiq),汇集所有参考点的特征指纹,形成一个特征位置指纹空间,则完成离线指纹库的建立。 GRNN是一个基于记忆和高度并行结构的一遍学习算法[20],GRNN由输入层、模式层、求和层和输出层组成,输入层为模式层的所有神经元提供输入数据,模式层采用高斯激活函数作为神经节点,从而具有非线性映射能力,求和层利用权重向量计算出输出层的估计值,结构框图如图3。 图3 GRNN框图Fig.3 GRNN block diagram GRNN引申于RBF,且与后者有相似的网络结构,但在分类和预测上,GRNN更有优势。GRNN 模型将连续变量的估计值收敛于回归曲面,无需迭代即可实现预测、建模以及映射。而RBF则需更多的神经元,才能较为精准地逼近。 对于一组给定的输入向量F=[λ1,λ2,…,λq]和输出向量L=[x,y],GRNN通过 Parzen[21]非参数估计可由实际样本集估算出概率密度函数f(F,L)为 (16) (16)式中:f(F,L)为模型参数spead的样本概率密度函数;m为样本数;q为输入向量的维数;spead为高斯函数的拓展系数;Fi和Li分别为第i样本的输入和输出向量。 基于已知的概率密度函数可由(17)式得到网络的输出L,即预测出待定位点的位置。 (17) (17)式中,L为所有样本观测值Li的加权平均,且权值系数直接由样本数据决定,训练过程依赖样本,从而能最大限度地避免人为假定[22]。 由于GRNN的概率密度函数是通过训练样本数据而得,因而具有较强的泛化性,适用于解决室内定位的问题。GRNN仅有一个自由参数spead,本文将通过交叉验证[23]来改变spead以调整网络性能,即找寻定位算法在定位准确性与适应性之间的平衡点,最终使定位的预测模型能正确地映射指纹—位置的关系。 在线定位阶段,采集测试点的CSI数据,并利用聚类的PCA算法提取特征位置指纹,作为GRNN模型的输入值,输出结果则为该测试点的估计位置。图4给出了基于聚类的PCA和GRNN的CSI指纹定位的流程。 图4 算法流程Fig.4 Algorithm flow 对于本文提出的算法,采集并验证了实际环境中实验数据。在采集数据时,利用一台2天线的TP-Link路由器作为发射端,一台装有3天线Intel 5300 NIC的笔记本电脑作为接收端,通过电脑中的内置网卡提取经由路由器转发的CSI信号,采集数据的电脑使用Ubuntu 10.04 LTS的操作系统。 实验环境选在辽宁工程技术大学实验楼2楼一个面积约为100 m2的移动通信实验室,屋内放有多套桌椅和实验器材,如图5。将AP固定在位于房间一侧高1.2 m的桌子上,同时接收设备的高度与AP高度保持一致。在实验区域内按相邻参考间隔为0.8 m的网格均匀布设126个参考点,每点采集500个数据包。不同时间下,随机选取30个位置重新采集100个数据包,作为在线阶段的测试数据,实验仿真在MATLAB R2015a上完成。表1给出了实验参数的具体数值。 表1 实验参数Tab.1 Experimental parameters 图5 实验区域布局Fig.5 Layout of experimental area 为了分析不同指纹特征对算法性能的影响,分别选用幅值、相位、联合指纹以及CSI数据包中含有的RSS值来描述位置特征。图6给出了不同特征指纹的定位性能。从图6中可看出,在相同环境下,将CSI作为指纹比RSS可取得更好的定位性能。采用RSS作为特征值,算法的定位精度在3~5.5 m;单独的幅值和相位值,可以实现的定位精度为2.5~4.5 m;而采用联合指纹后,定位误差基本可控制在2.5 m以内,其中84.5%的数据定位误差在1.5 m以内,而1 m内约占了52.2%。实验结果表明,采用CSI幅值和相位的联合指纹相较于单一的指纹特征具有一定的优势,同时也验证了本文对于原始指纹信息的处理在室内环境下可以提高位置指纹的可靠性和有效性。 图6 不同指纹的定位结果Fig.6 Positioning results of different fingerprints 根据已有研究表明[9,16],不同位置上CSI值的簇数由于受多径效应和信道衰落的影响而存在差异,大多数位置仅出现4个以内的CSI簇,但少数位置上的簇数高达19个,因此对于原始联合指纹集的划分依赖于聚类数K的取值。若K值较小,簇内信息相似度不高,不利于提高定位精度;而K值较大,迭代次数递增,聚类结果的准确性难以保证,不利于减少算法的执行时间。为了既能提取出用来描述位置多径特性的指纹信息,又能保证较准确的聚类结果,以避免因聚类误差对定位精度的影响。本文将K值分别设置为5,8,10,16,20,50来划分原始指纹集,并分别采用幅值、相位以及联合指纹作为特征来分析聚类数K对算法性能的影响,结果如图7。 图7 不同聚类数的定位精度Fig.7 Positioning accuracy of different clustering numbers 由图7可知,分别采用不同的聚类数对3种位置指纹进行聚类分析,进一步验证了联合指纹的算法性能优于单独的幅值和相位。对于聚类算法,当K为5时,簇内相似度低、簇间相似度高,表现出不佳的定位性能;当K为50时,不同特征指纹的定位性能均为最差,原因在于迭代次数较多易产生错误的聚类结果从而影响定位精度;而当K为8,10或16时,算法的定位精度相差不大,其中,K为10表现为最佳性能。当K取不同值时,算法的迭代次数有所不同,因而所需的计算时间也不同,表2给出了不同K值下聚类算法所执行的时间。随着聚类数的增加,对于联合指纹的定位精度没有显著的变化,而算法的迭代次数却在增加,即增加了算法的执行时间。综合考虑,聚类数K的值为10时,算法的性能最佳,且所需的计算时间也相对较少,故本文将K设置为10以进行下一步的实验验证。 表2 不同聚类数的执行时间对比Tab.2 Comparison of execution time with different clustering numbers 考虑高维数据的PCA算法的累计贡献度w对算法的定位精度和计算时间的影响。图8给出了定位精度和计算时间随高维数据的PCA算法的累计贡献度w的变化情况,实验结果表明,随着w从90% 提高到99%,算法的平均定位误差在降低,而算法的回归时间却在递增。当w达100%时,即代表未使用高维数据的PCA提取子数据集的主成分,此时虽然可以实现较好的定位精度(平均定位误差为1.34 m),但算法的时间成本最大,即一个样本的执行时间为2.58 ms。而与w为100%的情况相比,w为99%时的平均定位误差最好(为1.23 m)且一个样本的执行时间仅需0.78 ms,故本文将累计贡献度w设为99%,此时算法的定位性能最佳。 图8 累积贡献度w对定位精度和执行时间的影响Fig. 8 Influence of cumulative contribution w on positioning accuracy and execution time 为了验证本文所提算法的性能,将该算法与3种不同的定位算法进行比较:CSI-PCA,DeepFi和CSI-MIMO。为了保证4种算法在定位精度和定位效率等方面具有可比性,均在相同数据集(即本文所采集的实际数据)的基础上进行实验验证。图9为4种不同算法的定位误差累计概率分布,其中,本文所提算法在定位精度方面比其他3种算法有一定的优势。本文算法在1.5 m以内的定位误差累计概率为84.5%,分别比CSI-PCA,DeepFi和CSI-MIMO提高了8.2%, 13.1% 和29.8%,且本文算法基本可以将95%的数据的定位误差控制在2.5 m以内。CSI-MIMO采用多天线、多链路传输的CSI信号,并未对原始数据处理分析;DeepFi采用深度学习来训练CSI幅值集,未涉及相位信息;CSI-PCA利用SVM预测的位置局限于数据集的规模。而本文算法利用聚类PCA算法提高指纹间的区分度和可靠度,通过GRNN提高全局收敛性,进而有效地提高了算法的定位精度。 图9 4种室内定位算法的定位精度比较Fig.9 Comparison of positioning accuracy with four indoor positioning algorithms 表3对4种算法的执行时间做了进一步说明。由表3,本文算法与CSI-PCA算法的执行时间相近,而CSI-MIMO所需时间最短,DeepFi所需时间最长。主要原因在于CSI-MIMO算法中利用MIMO技术聚合了每个子载波的CSI值,将一个多天线、复杂的CSI信息转为简单向量,从而减少了时间开销;而在DeepFi算法中,虽然分包、分批地处理数据包,有效减少了算法的执行时间,但在对权值进行微调的过程中,需多次利用反向传播算法,而多次反向迭代使得DeepFi在4种算法中的执行时间最长。虽然本文算法与CSI-PCA在时间开销上相差不大,但仍有一定的优势,2种算法都利用了PCA算法对高维数据进行处理,降低了数据维度、减少了时间开销,而在定位算法的选择上,GRNN比SVM中的RBF有着较快的收敛速度,因而本算法所需的执行时间要小于CSI-PCA算法。 表3 4种算法的执行时间对比Tab.3 Ccomparison of execution time with 4 different algorithms 为解决复杂多径环境下定位精度低的问题,本文提出一种基于聚类的PCA和GRNN的CSI指纹定位算法。通过实验验证表明,联合指纹比单一的特征指纹在定位精度方面具有一定的优势。该算法利用改进的K-means聚类算法划分原始联合指纹集可有效地分离CSI数据携带的多径信息,同时利用高维数据的PCA算法进行特征提取可将算法的定位精度提高8.2%,且一个样本的时间开销减少1.8 ms。此外,利用GRNN模型对特征指纹进行充分地学习,使得本文所提算法在定位精度方面均优于CSI-PCA,DeepFi和CSI-MIMO 3种算法,证明了本算法的可行性和可靠性。本文的研究虽具有一定的成效,但还不够深入全面。在后续的研究中,我们将从现有的单点定位向多点的轨迹定位方向展开工作。
2.3 指纹库构建
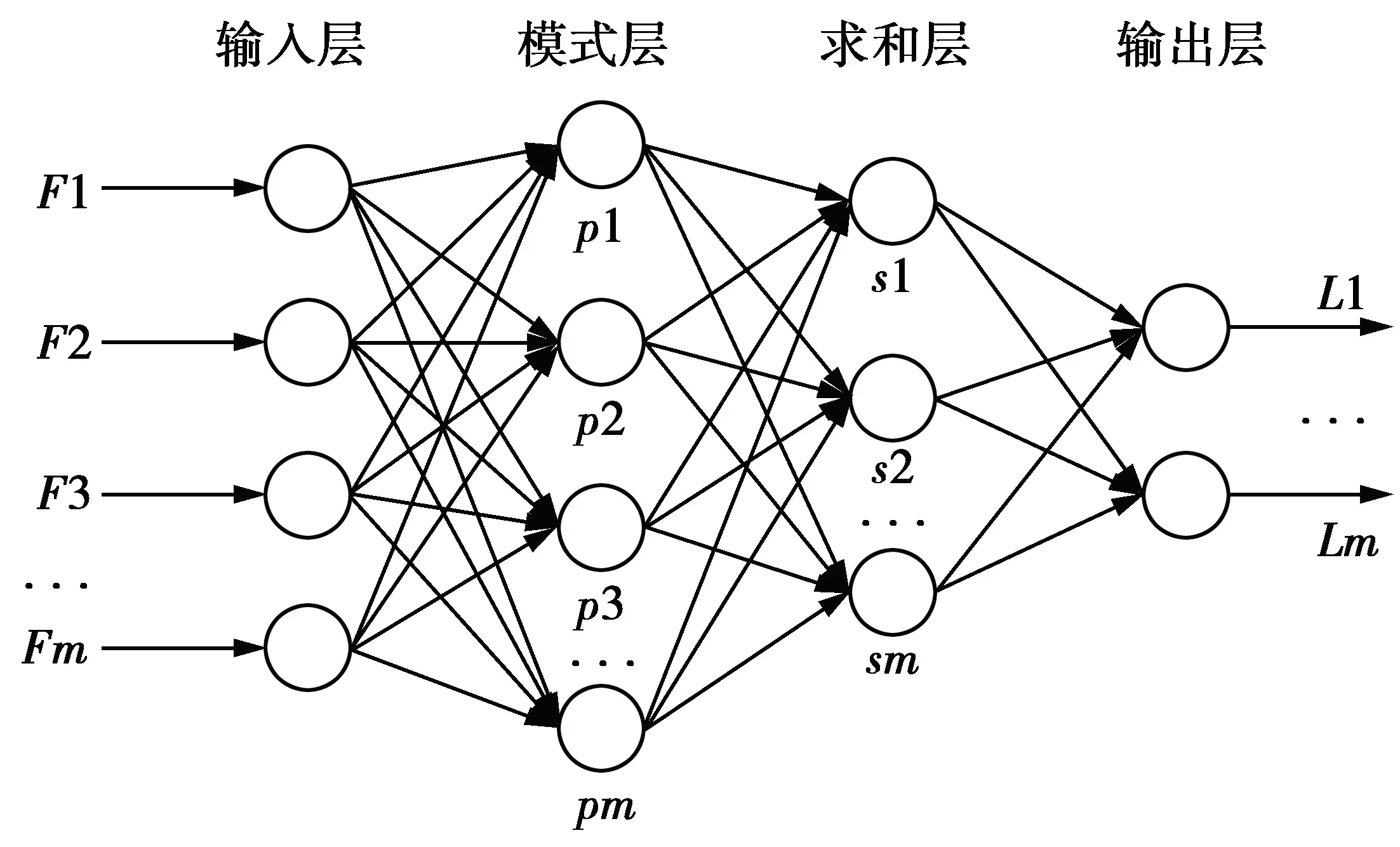
3 广义回归神经网络
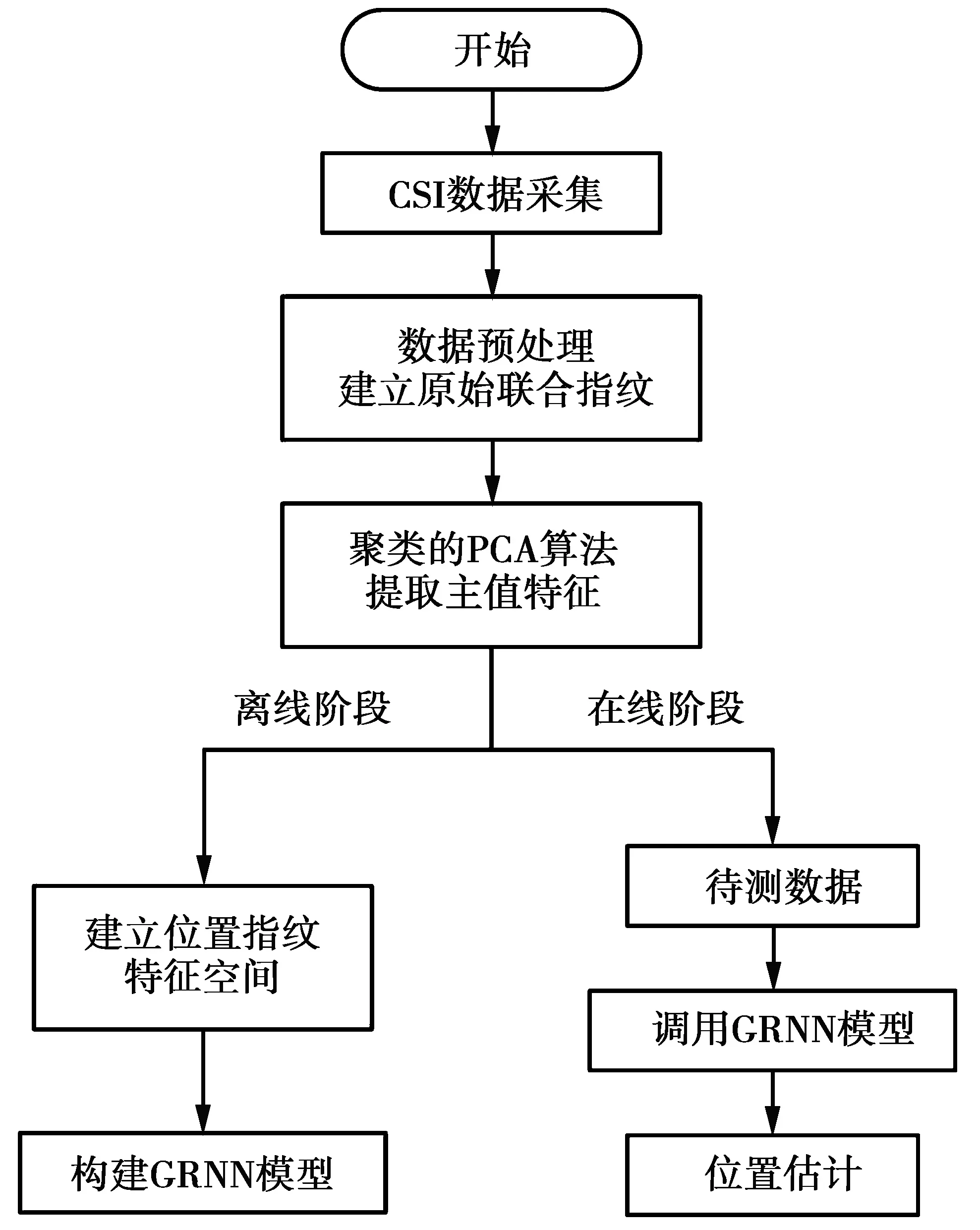
4 实验结果分析
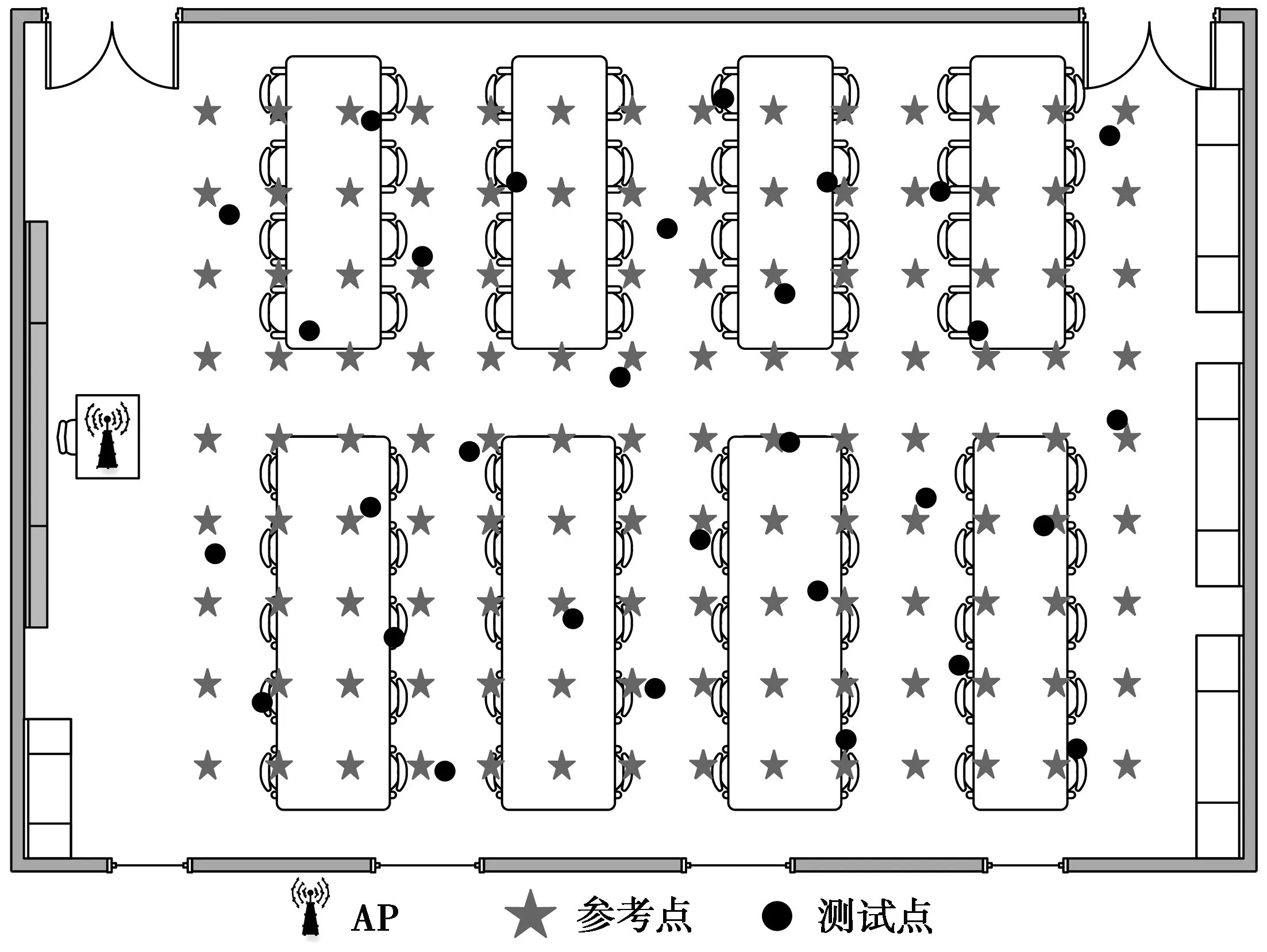
4.1 实验环境

4.2 不同指纹特征对算法性能的影响
4.3 不同聚类数对算法性能的影响

4.4 不同累计贡献度对算法性能的影响
4.5 不同定位算法的性能比较

5 结束语

