一类带有变指数增长的Neumann问题
蒙 璐,储昌木,雷 俊
贵州民族大学 数据科学与信息工程学院,贵阳 550025
考虑如下非线性Neumann问题:
(1)
其中Ω⊂RN(N≥3)是边界光滑的有界域,
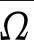
(2)

(f1) 存在常数a>0和0<σ<1,使得对任意(x,s)∈Ω×R,|f(x,s)|≤a|s|σ;

近年来,对具有Neumann边界的椭圆型偏微分方程的研究引起了许多学者的注意,也获得了一些新的成果(见文献[1-10]).此外,文献[11]研究了如下带有变号位势的Neumann问题:
其中Ω是RN中光滑的有界域,p>1,a(x)是Ω上变号的连续函数,并利用约束最大化方法探讨了半线性椭圆型问题正解的存在性.
文献[12]研究了以下问题:
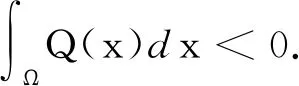
问题(1)对应的泛函为
其中u∈H1(Ω),
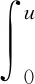
由文献[10]知,H1(Ω)可作直和分解
H1(Ω)=R⨁V
其中
对u∈H1(Ω),有u=t+v,其中v∈V,

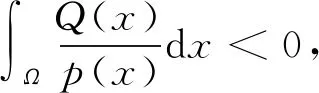
时,有
证若不然,则对∀n∈N,存在tn∈R,vn∈V,使得当
时,有
(3)
或
(4)

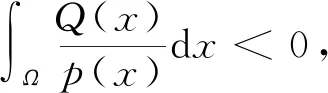
由ωn在Lp-(Ω)和Lp+(Ω)上均趋于0知

当|tn|≤1时,对∀x∈Ω,|tn|p+-p-≤|tn|p(x)-p-≤1.(4)式两边同时除以|tn|p-,可得
即
同样,当n→∞时,有

综上所述,引理1的结论成立.
引理2假设条件(f1),(f2)和(2)式成立,则存在λ*,β,ρ>0,使得对任意λ∈(0,λ*),有:
证当|t|≤1时,对某一固定的η>0,若‖v‖2≤η|t|,则由引理1可知
其中
因此
(5)
(6)
由Sobolev不等式知,当‖u‖V=ρ<1时,存在常数C1>0,使得
故当‖u‖V=ρ<1时,
取
就有
由‖u‖V=ρ和(6)式,有
(7)
由条件(f1)知,存在常数C(ρ)>0,使得
因而,对‖u‖V=ρ,存在λ*>0,当0<λ<λ*时,有
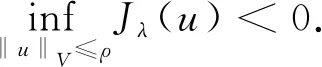
由mes(Ω1)>0,则
注意到p->2,当t→∞时,Jλ(tv0)→-∞.取t1充分大,使得ω=t1v0满足‖ω‖≥ρ,则Jλ(ω)<0.
引理3假设条件(f1),(f2)和(2)式成立,则存在Λ*>0,使得0<λ<Λ*时,Jλ满足(PS)条件.
证设{un}是H1(Ω)中的任一(PS)序列,则存在c>0,使得当n→∞时,有
(8)
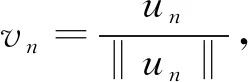
由(8)式可得
(9)
(10)
由条件(f1)知
由于‖vn‖=1,则存在C≥0,使得
故当n→∞时,
类似地可以推出,当n→∞时,
由此,
则当n→∞时,可得
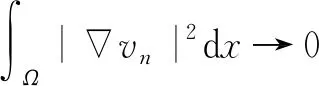
取任意的i,j∈N,就有
又因为

定理1假设条件(f1),(f2)和(2)式成立,则存在λ*>0,使得0<λ<λ*,那么问题(1)有两个非平凡解.
证由引理2知

由山路引理知,问题(1)存在另一个解u2,满足Jλ(u2)=cλ>0.由于
Jλ(u1)<0=Jλ(0) 故u1和u2是问题(1)的两个不同的非平凡解.

