Hydrogen-induced dynamic slowdown of metallic glass-forming liquids∗

Jin-Ai Gao(高津爱), Hai-Shen Huang(黄海深), and Yong-Jun L¨u(吕勇军)

School of Physics,Beijing Institute of Technology,Beijing 100081,China

Keywords: metallic glasses,hydrogen,dynamics

1. Introduction

Metallic glasses have potential application in the fields of hydrogen storage and biomaterials.[1,2]Understanding the influence of hydrogen on the properties of metallic glasses is of importance for optimizing the performance of the materials. Experimental and simulation studies have shown that the hydrogen microalloying has beneficial effect on glassforming ability (GFA) and mechanical properties of bulk metallic glasses (BMG). For example, both GFA and malleability of Zr-based BMG are improved by doping hydrogen due to strong binding to Zr.[3,4]In contrast, Pd-based BMG shows low hydrogen affinity and thus the effect of hydrogen doping is less significant.[5]Ab initiomolecular dynamics (MD) simulations have revealed that a small addition of H atoms can decrease the icosahedral order and slow down the atomic mobility in CuZrAl glass.[6]Experimental results argued that more large free volume regions collapse by the addition of hydrogen and the denser random packed structure is formed,thus enhancing GFA.[7]In addition,the doping of hydrogen was found to enhance the diversity of locally ordered structures, which was believed to be responsible for the improved ductility.[8]In fact, the performance modification of metallic glasses via hydrogen doping largely depends on the concentration of hydrogen. With increasing addition of hydrogen,the thermal stability of metallic glasses inevitably becomes poor, ultimately leading to crystallization. The amorphous Cu–Zr alloy has been proved to be decomposed into a mixture of crystalline phase Cu, CuxZrycompound and ZrH2at high temperature and high hydrogen pressure.[9]In most cases, the effect of hydrogen has been involved in the preparation stage of metals, where the melts are quenched in the protective atmosphere composed of a small amount of hydrogen as reductant.[10,11]The effect of hydrogen doping on properties of supercooled glass-forming liquids therefore should be clarified first. In this work, we optimize the potential parameters of Cu/Zr/H system within the framework of modified embedded atomic method(MEAM).Based on the interatomic potential,we study the dynamic properties of hydrogen doped Cu50Zr50glass-forming liquids using MD simulations,and reveal the structural origin of hydrogen-induced dynamic slowdown.

2. Computational methods

2.1. MEAM potential for Cu/Zr/H system

We use the MEAM potential to describe the interactions between hydrogen and metallic base in MD simulaitons. This model was first proposed by Baskeset al. In the MEAM,the total energy of a system is approximated as a sum of the pairwise interaction and the embedding energy as a function of background electron density by taking the bonding directionality into consideration.[12,13]For liquid systems, the MEAM potential shows a good application provided appropriate parameters or functional forms. Also, the MEAM potential is capable of describing the bonding characteristic of hydrogen and metallic elements,thus it is preferred in this work. Leeet al.developed an original version of the MEAM potential for Cu/Zr/H system.[14,15]The calculations based on their parameters show that the energies of Cu–Zr as well as the diffusion of hydrogen are not sufficiently accurate. Therefore, at first, we optimized the MEAM parameters based on Lee’s work. The present training set is composed of several Cu–Zr compounds and Cu and Zr hydrides. We used the single parameter optimizer in training. Tables 1–3 provide the MEAM parameters for Cu/Zr/H developed in this work.

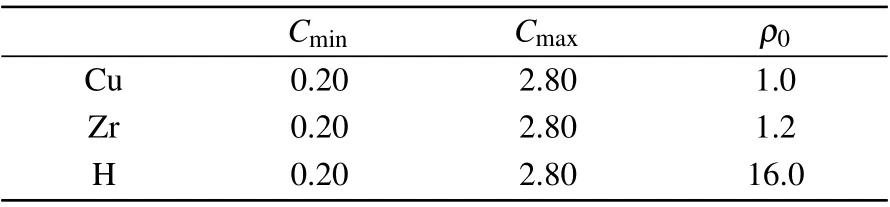
Table 1. 2NN MEAM potential parameters sets for pure Cu,Zr,and H.

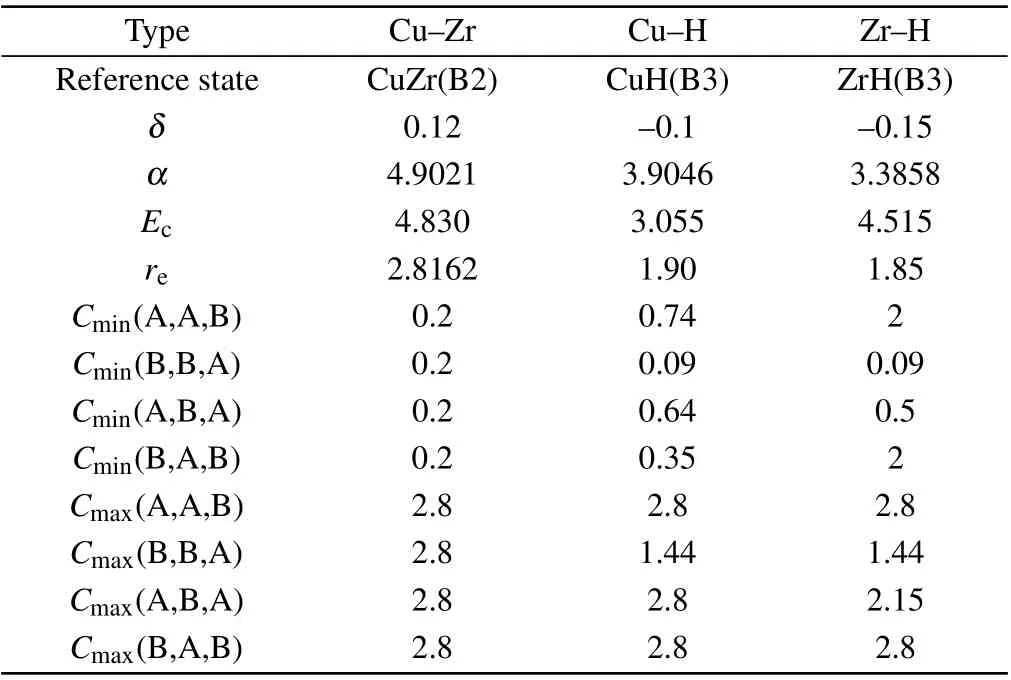
Table 2. 2NN MEAM potential parameters for the binary M–M and M–H(M=Cu,Zr)systems.

Table 3. Parameter sets of Cmin and Cmax for Cu–Zr–H system.

We first check the application of the present MEAM potential in describing the energy and structure of Cu–Zr systems. Here,the embedded atomic method(EAM)potential[16]for Cu–Zr alloys developed by Mendelevet al.is used as a reference, which has been proved to have high accuracy in reproducing various properties of Cu–Zr liquids and glasses.Figure 1 shows that the present MEAM potential well predicts the potential energies of Cu50Zr50over the range from hightemperature liquid state to glass state compared to the results from reported MEAM potentials. Based on the temperature dependence of the potential energies, our model predicts that the glass transition occurs atT=733 K,which is much close to the value ofT=736 K by the EAM potential and better than the result ofT=768 K predicted by Lee’s potential. Table 4 provides the comparison of the nearest neighboring distance in Cu50Zr50glass. The value for Cu–Zr pair predicted by our model potential is more consistent with the experimental and EAM results. We further check the diffusion coefficients of hydrogen in face-centered cubic (fcc) Cu and body-centered cubic/hexagonal close-packed(bcc/hcp)Zr by referring to experimental data. The results shown in Fig.2 indicate that the present MEAM parameters have a better application of predicting hydrogen dynamics. The above comparisons confirm that the MEAM potential developed in this work can more reasonably describe the interactions among Cu,Zr,and H,especially in liquid and glassy states.

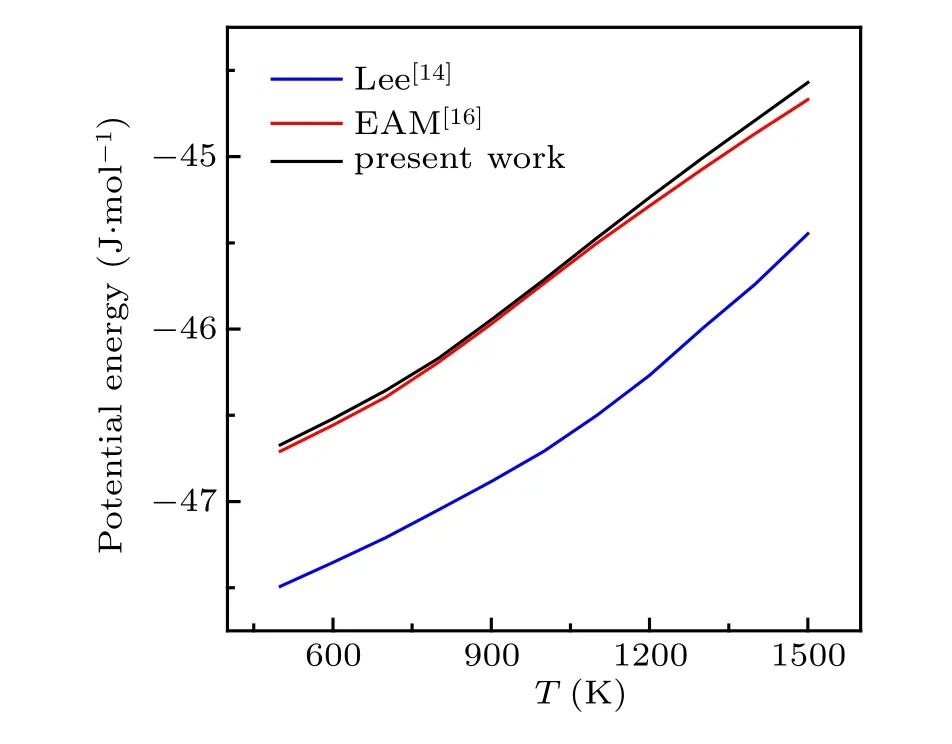
Fig.1. Comparisons of potential energies of Cu50Zr50 between MEAM and EAM potentials.

Table 4. Nearest neighboring distances of Cu–Cu, Zr–Zr, and Cu–Zr pairs in Cu50Zr50 glass at T =300 K.

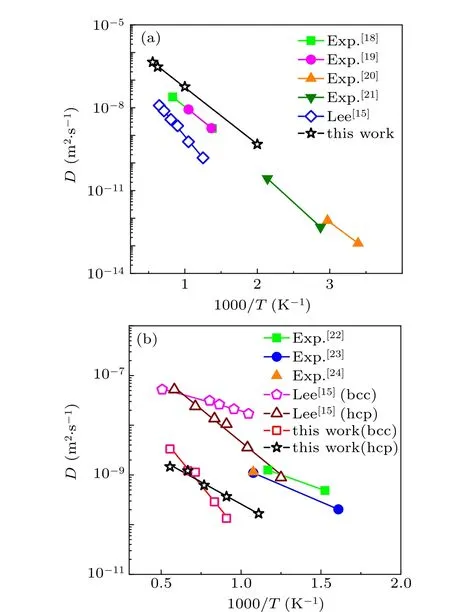
Fig. 2. Self-diffusion coefficients of hydrogen atom in (a) fcc Cu and(b) bcc/hcp Zr predicted by MEAM potentials in comparison with experimental data.

2.2. MD simulations

The quenching processes of (Cu50Zr50)100−xHx(x=0–10) were simulated by using MD simulations based on the newly developed MEAM potential. The systems consisting of 10976 atoms were equilibrated at 1800 K and then quenched to 500 K at zero pressure with a cooling rate of 0.1 K/ps,i.e.,a relaxation of 1 ns every 100 K.The MD simulations were performed in the isothermal and isobaric ensemble (NPT) with the periodic boundary condition along the three dimensions and a time step of 0.25 fs was used.

3. Results and discussion

3.1. Dynamic properties of(Cu50Zr50)100−xHx system

For the H-free Cu50Zr50melt,the calorimetric glass transition temperatureTgis 733 K under the present simulation conditions. The addition of H is found to universally increaseTgto 800±10 K. Clearly, the melt is more easily quenched into glassy state with hydrogen, which is consistent with the experimental results of CuZrNiAl alloy.[7]We analyze the relaxation dynamics of supercooled melts by calculating the intermediate self-scattering function(ISF)

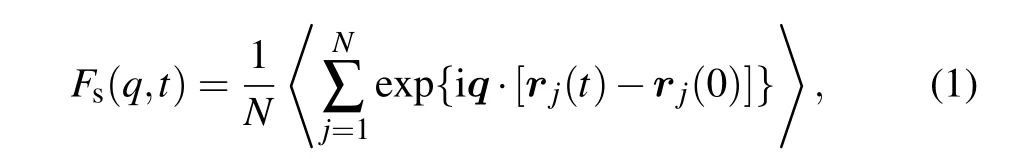
whereqis the wave vector,and|q|=2.688 ˚A−1corresponding to the first peak of the static structure factor. The structural relaxation timeταis estimated by the time decaying to 1/e.[25]Figure 3 shows the logarithm plot of the relaxation time as a function of the inverse of temperature upon approaching glass transition. The relaxation is shown to be slowed down by doping H atoms, and moreover, it is more pronounced with increasing concentration of H.All the temperature dependences of relaxation time obey the Vogel–Fulcher–Tamman law(VFT)[26]τα=τ0exp[DTT0/(T −T0)].However,the fitted values of the parameterDTincrease from 0.877 for the H-free,1.028 for 2 at.% H to 1.211 for 8 at.% H. It means that the supercooled liquid becomes stronger with more H atoms.

Fig. 3. Logarithm relaxation time as a function of the inverse of temperature,and the solid lines are fits to VFT law.

The fragility of supercooled liquids can also be measured from a thermodynamic point of view. We calculate the specific heatCpin the NPT ensemble through glass transition. In general,the abrupt decrease of specific heat across glass transition varies with the fragility of supercooled glass-forming liquids: considerable changes in stronger glass formers but small ones in fragile formers like GeO2.[27,28]Figure 4 shows that ∆Cprises significantly with increasing content of H,from 9.170 J·mol−1·K−1to 10.629 J·mol−1·K−1for 2 at.% and 14.128 J·mol−1·K−1for 8 at.%. It indicates that the liquid becomes stronger as more H atoms are added, which is consistent with the results from the dynamic fragility in Fig. 3.On the other hand, the contribution of the thermal motion of H atoms is ignorable considering its very small amount,thus,the rise of ∆Cpactually implies that the addition of H atoms induces more complex atomic motions of base elements.

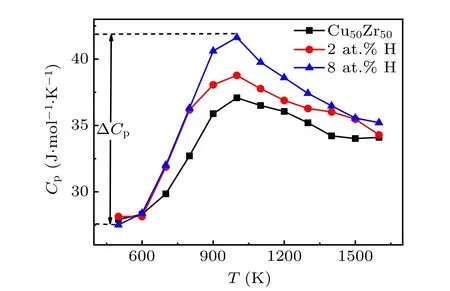
Fig.4. Specific heat as a function of temperature at different concentrations of hydrogen across glass transitions.

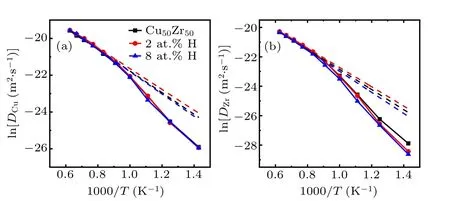
Fig. 5. Logarithm plots of diffusion coefficients of (Cu50Zr50)1−xHx(x=0,2,8)as a function of the inverse of temperature. (a)Cu and(b)Zr. The dashed lines are fits to the Arrhenius relation.

Figure 3 reflects the slowdown of the overall structural relaxation. To clarify the chemical dependence of the dynamic slowdown, we calculate the self-diffusion coefficients of Cu and Zr during quenching, respectively, which is given by the long-time limit of the mean squared displacements[29]

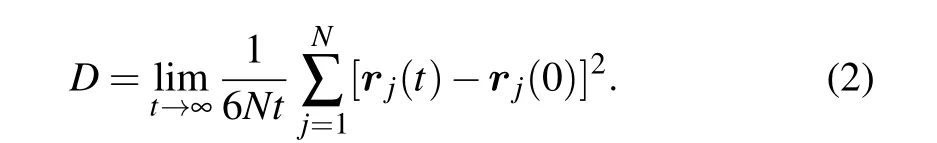
Figure 5(a) shows that the diffusion of Cu atoms is not markedly influenced by the addition of H atoms.The Cu diffusion coefficients in both H-free and H-doped systems display approximately the same super-Arrhenius temperature dependence. In contrast,the diffusion coefficients of Zr atoms have a distinct decrease with increasing content of H,displaying a growing deviation from the Arrhenius relation, as shown in Fig. 5(b). It is clear that the dynamic slowdown of Cu50Zr50melts is mainly contributed by more sluggish Zr atoms due to the doping of H. In short, the addition of H atoms is able to slow down the diffusion,relaxation process of base melts and make the system stronger.

3.2. Structural characteristics of(Cu50Zr50)100−xHx melts

We aim to reveal the structural origin of the slowdown dynamics. We analyze the local structure of supercooled liquids using the Voronoi polyhedron method. For glassy systems,icosahedrons were believed to be of importance in featuring local structure, and therefore were often taken as the characteristic quantity to understand the relation between structure and dynamic properties.[30]More general, the dynamic properties were found to be closely related to the local five-fold symmetry associated with Voronoi polyhedron,[31]which is defined asW=∑i(f5i×Pi),wheref5irepresents the proportion of pentagons,f5i=n5i/∑inki,nki(k= 3, 4, 5, 6) is the number ofk-side polygons in Voronoi polyhedroni,andPiis the fraction of Voronoi polyhedroni. We count the number of various polyhedrons in supercooled liquids, and find that the polyhedrons with high five-fold symmetry rank in the top ones regardless of the addition of H atoms. It is consistent with the locally structural characteristics of metallic glasses,whereas the fractions of these polyhedrons have a overall decrease with increasing content of H.Figure 6 presents the average five-fold symmetry in the melts as a function of temperature. It shows a distinct decrease as more H atoms are doped. These results indicate that H atoms tend to decompose the local five-fold symmetry structure,which agrees with the reportedab initiosimulations.[7]The five-fold symmetry structure was argued to facilitate the glass transition due to the frustration of crystallization.[32]Obviously,its reduction is contradictory to the fact that the glass transition is enhanced in the present simulations. In addition,we find that the high fivefold symmetry polyhedrons are not decomposed into denser packing structure. Figure 7(a) shows that the average atomic volumeVactually is increased by doping H atoms. It suggests that H atoms segregate in interstices of polyhedrons and result in the expansion of atomic volumes for both Cu and Zr,forming more large-volume polyhedrons. Such volume expansion is relatively weak and does not significantly change the global structure of the base alloys, as evidenced by the radial distribution functions (RDFs) for Cu–Zr, Cu–Cu, and Zr–Zr pairs shown in Fig. 7(b). Although that, Fig. 4 clearly shows that the atomic mobility is slowed down. Therefore,more intrinsic structural cause is needed to resolve these contradictions.

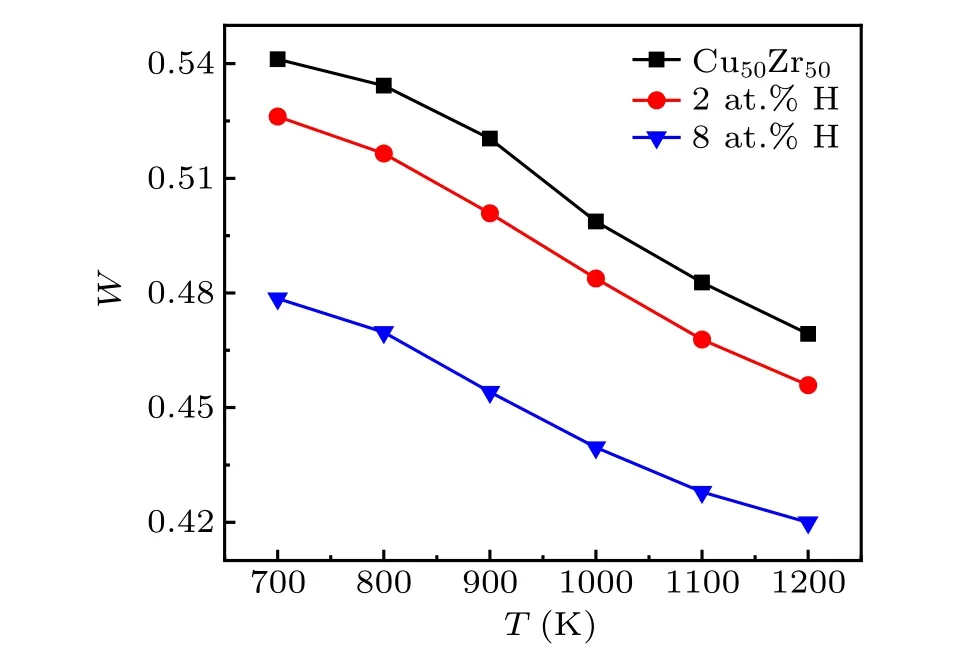
Fig.6. Average five-fold local symmetry of(Cu50Zr50)1−xHx (x=0,2,8)versus temperature.

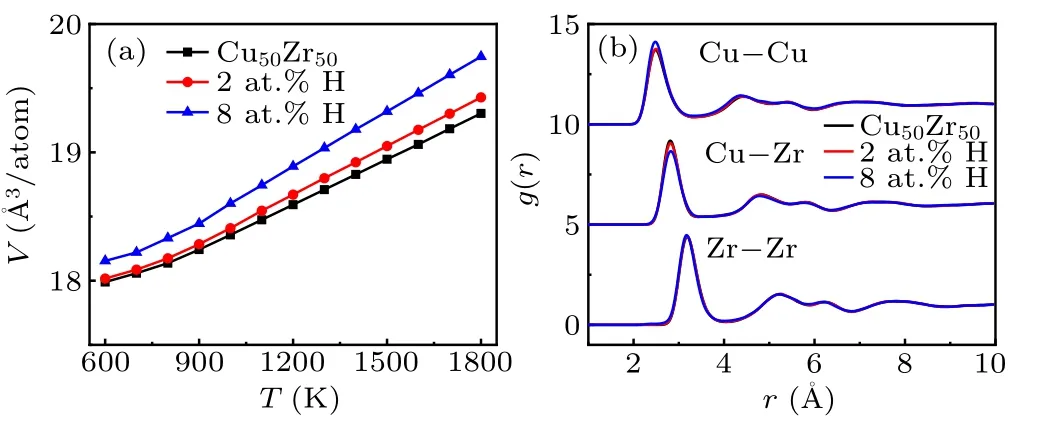
Fig.7. (a)Average atomic volume as a function of temperature for Hfree,2 at.%and 8 at.%H systems. (b)Partial RDFs of Cu–Zr,Cu–Cu,and Zr–Zr pairs at T =500 K.

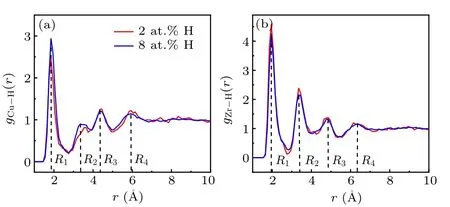
Fig.8. Partial radial distribution functions of(Cu50Zr50)1−xHx (x=2,8)at 500 K.(a)Cu–H pair and(b)Zr–H pair.

Experimental and numerical studies have found that the relative peak positions in RDFs of metallic glasses are identical with the values of their crystalline counterparts,which suggests that disordered systems may hide the translational order inherited from crystal phases.[31,32]It is possible that there is a competition between the five-fold symmetry and the crystalline ordering in metallic glasses. To some extent H atoms tend to bond to base elements,forming metal hydrides,in particular with Zr atoms. We explore this possibility by means of RDFs. Figure 8 shows the partial RDFs of Cu–H and Zr–H pairs. We calculate the peak positions relative to the nearest neighboring distance,and compare them with several typical hydride compounds.[33,34]We find that the second, third,and forth relative peak positions of Zr–H pairs have a good match with those of ZrH3;[35]comparatively,for Cu–H pairs,the second and third relative peaks match with those of CuH compound but a bit large deviation is found in the forth peak position, as listed in Table 5. The translational order associated with crystal phases indeed exists between H and metallic components, especially between Zr and H. To further reveal the hidden ordering, the bond angle distributions around Zr atoms are provided in Fig.9.[36]

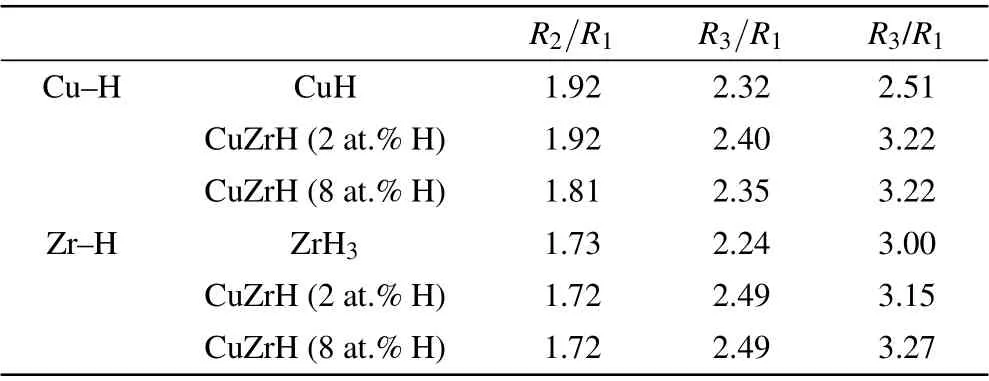
Table 5. Ratios of the second,third,and fourth peak positions in RDF to the nearest neighboring distance for Cu–H and Zr–H pairs.

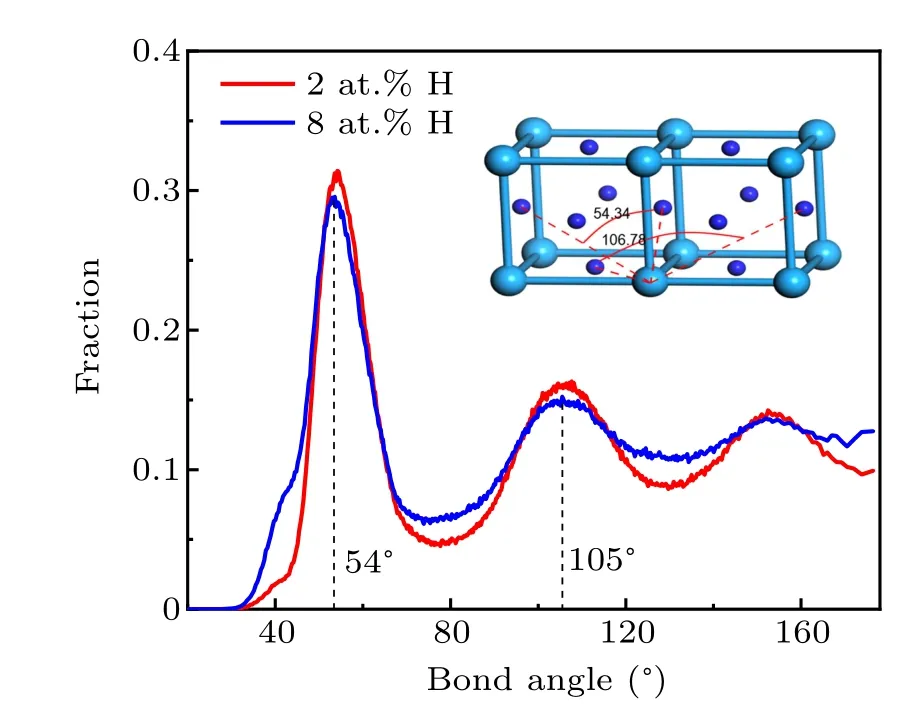
Fig. 9. Distributions of bond angle centering Zr atoms in supercooled CuZrH liquids at T =700 K.The inset schematically illustrates the structure of ZrH3 compound. The cyan and blue balls denote Zr and H atoms.

The bond angle at the first peak well corresponds to the value of ∠HZrH (∼54◦) in the nearest neighboring distance of ZrH3, and the one at the second peak corresponds to the∠HZrH in the second nearest neighboring distance of ZrH3(∼106◦). Therefore, the orientational order also exists between H and Zr. In fact, ZrH3has stronger cohesive energy among Zr hydrides, and it is more stable at high Hconcentration. The tendency of forming ordered bonds between Zr and H induces the slowdown of Zr mobility,despite that the atomic volume is expanded. Meanwhile, we analyze the spatial distribution of H atoms and find that more H atoms segregate around Zr atoms with decreasing temperature, for example, exceeding 60% in 2 at.% system at 800 K. Therefore,the interactions between Zr and H play a primary role in H-induced dynamics. The addition of H atoms destroys the high five-fold symmetry polyhedron, and on the other hand,the bonding between Zr and H slows down the dynamics. The tradeoff between them determines the dynamic behavior and thermal stability. In the case of small addition of H atoms,the latter is dominant and the dynamics of the melts becomes slow.Furthermore, due to the ordered bonding, more thermal motion modes are expected in the base metals,which provides an explanation for the increasing ∆Cpacross glass transition with increasing H content. In simulations,we increase the concentration of H up to 10 at.%and find that more H atoms tend to segregate, which will inevitably influence the phase stability.If the H concentration is further increased, the crystallization of metallic hydrides is expected to occur.

4. Conclusion

In summary, we optimize the MEAM potential parameters of Cu/Zr/H system. The newly developed parameters show a better application of describing the structure and dynamic properties of Cu/Zr/H system. Based on the potential,we use MD simulations to study the dynamics of H doped Cu50Zr50liquid. The results reveal that the doping of H atoms in the supercooled glass-forming liquid induces the slowdown of structural relaxation and stronger liquid state. The dynamic changes are closely related to the interplay between H and Zr atoms. Structural analyses indicate that the local five-fold symmetry is reduced by adding H and ordered bonding between Zr and H is enhanced. The latter is the dominant cause for the slow dynamics and the enhanced glass transition. This work is helpful to comprehensively understand the dynamics of H-metallic glass systems as well as its structural origin.