ℋ∞state estimation for Markov jump neural networks with transition probabilities subject to the persistent dwell-time switching rule∗

Hao Shen(沈浩) Jia-Cheng Wu(吴佳成) Jian-Wei Xia(夏建伟) and Zhen Wang(王震)

1College of Electrical and Information Engineering,Anhui University of Technology,Ma’anshan 243032,China

2School of Mathematical Sciences,Liaocheng University,Liaocheng 252059,China

3College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao 266590,China

Keywords: Markov jump neural networks, persistent dwell-time switching rule, ℋ∞state estimation, meansquare exponential stability

1. Introduction

Over the past few decades, neural networks (NNs) have drawn considerable interest of many researchers, mainly owing to its significant potential applications in many domains,such as image restoration,fault detection,and classification of patterns.[1–7]In the study of NNs,it has been realized that the parameters of NNs may stochastically switch due to external or internal changes,such as random component faults and unexpected environment variations.[8–15]As is well-known, the Markov chain has been extensively utilized to character the jumping behavior that displays the stochastic feature.[16–18]Thus,Markov jump NNs(MJNNs)are quite suitable for modeling the randomly jumping NNs with multi-modes. The studies about MJNNs are becoming more and more pervasive,and there are many remarkable results on MJNNs that have been made,see in Refs.[19–21],and the references therein.

In fact, much current work on MJNNs depends on the hypothesis that the transition probabilities (TPs) are timeinvariant. However, this hypothesis may be inapplicable to many practical applications where TPs are time-variant because of the diverse changes in the external environment.Therefore, researchers have turned to a more general kind of TPs in the Markov chain that can better describe the random phenomenon. Typically, a reasonable way is to introduce the nonhomogeneous TPs. By virtue of the piecewise constant TPs, we are going to make efforts on it. Then, in one study in Ref. [14], the authors obtained some sufficient conditions for the stability of Markov jump linear systems whose TPs satisfy a dwell-time (DT) constraint. Then, the DT switching rule(DTSR)demands that the all switching interval must be no less than a positive constantτDT,which is unable to describe the situation where activation times of some subsystems are less thanτDT. Moreover, the average dwell-time switching rule (ADTSR) was used to characterize the variation of TPs for MJNNs in Ref.[22]. The ADTSR allows that the duration between two sequential switching instants can be less than a positive constantτADT,which relieves the restriction of the DTSR to a certain degree. Persistent dwell-time (PDT)switching, which displays more general switching characteristics, includes the fast and slow switchings, simultaneously.There is still little research about the issue of TPs subject to the PDTSR, although the PDTSR is regarded to be more general than the DTSR and ADTSR in some degree.[23,24]In practice, due to the influence of some external environment,the Markov chain may exhibit a characteristic,that is,TPs are time-varying but invariant in some segments. Thus,introducing a Markov chain with piecewise constant TPs is of great significance, which has not been fully studied. In addition,the PDTSR,as a more general switching rule,can be changed into the DTSR and ADTSR by selecting the corresponding parameters. This motivates us to use the PDTSR to describe the piecewise constant TPs for MJNNs.

In practice,the obtained state information is not complete in most of the research about MJNNs mainly because the states of systems are unmeasurable,or there is a large error between the measured and the actual signals. Therefore,it is necessary to construct a state estimator to obtain complete information about system states. Moreover,there are fruitful results focusing on this issue in Refs.[25,26]. To name a few,the authors have studied the issue of the non-fragile state estimation for discrete-time NNs with Markov jump parameters and time delays in Ref. [27]. Theℋ∞asynchronous state estimation for fuzzy MJNNs with uncertain measurements has been investigated in Ref. [28]. Furthermore, the problem of the exponential state estimation for MJNNs with time-varying discrete and distributed delays has been discussed in Ref.[29]. As for discrete-time MJNNs with TPs subject to the PDTSR,the corresponding results on the state estimation issue are quite few.This motivates our great interest in coping with this issue.

Motivated by the above discussions, we mainly concentrate on the design of the state estimator for MJNNs. Distinct from the existing state estimation methods in Refs. [22,27],we make the first attempt to deal with theℋ∞state estimation issues for discrete-time MJNNs with TPs subject to the PDTSR, where the mode-dependent estimator is considered.In order to model a more general scenario, we introduce the PDTSR to characterize the time-varying TPs, rather than the DT and ADTSR frequently studied previously. Moreover,through the Lyapunov stability theory and stochastic analysis method,some sufficient conditions that ensure the stability and the desired property of the estimation error system(EES)are proposed in this paper.

The undermentioned content of this paper is arranged as follows. The system modeling and PDTSR are elaborated in detail in Section 2. Some criteria are obtained in Section 3 on the mean-square exponentially stability with anℋ∞performance attenuation level for the EES.In addition,a numerical example is presented to show the correctness of the developed method in Section 4. Finally, the summary of this paper is given in Section 5.

Notations: The notations used in this work are standards in Ref.[22].

2. Preliminaries and problem formulation

2.1. System model

Considering probability space(∆,ℱ,Pr)in this study,the discrete-time MJNNs are depicted by the following equalities:

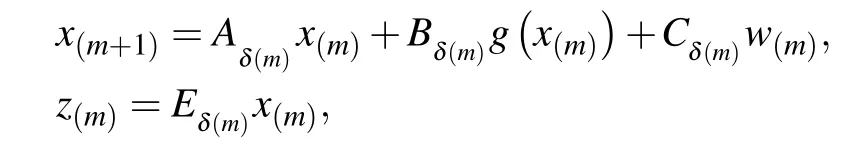
Remark 1 It is worth pointing that MJNNs consist of finite modes, which switch due to the external uncertainty change,[30]and the parameters of the estimator are modedependent,whose mode is in line with the underlying system.In this study,the PDTSR is adopted to characterize the change of the piecewise time-varying TPs. In addition,the switching signalϑ(m)andδ(m)are two different switching signals,which obey different switching rules,but they affect EES(3)simultaneously.

To present further,the following definitions and a lemma are provided.

Definition 1[31]If there exist scalarsρ ＞0, 0＜ζ ＜1,such that for∀ς(0)∈Rn,δ(0)∈ℳ,andϑ(0)∈J,the following inequality

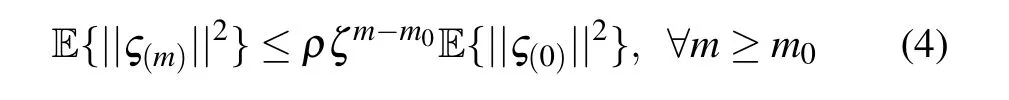
holds forw(m)≡0,then,EES(3)is mean-square exponentially stable(MSES).

Definition 2[32]Given constantγ ＞0, if EES (3) is MSES,and under zero-initial conditions

satisfy for nonzero∀w(t)∈l2[0,∞), then, EES (3) is MSES and meets a desiredℋ∞performance indexγ.

Lemma 1[33]Assume that the neuron activation functiongi(·),i={1,2,...,n}, is continuous and bounded,gi(0)=0,and satisfies

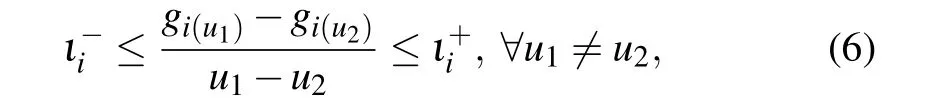
whereu1,u2∈Rn,andι−i,ι+iare known constants,then,for positive mode-dependent matricesΓi,there exist the following inequalities:

2.2. PDT switching and Markov jump mechanism

In this paper, the variation of system parameters is governed by Markov chain whose TPs are assumed to be nonhomogeneous, and the PDTSR is employed to characterize the alteration feature of TPs. The element of the transition probability matrix(TPM)can be expressed as

To facilitate the subsequent analysis,the definition of the PDTSR is provided.

Definition 3[31]For two positive integersτPandTP,the switching signalϑ(m)complies with the PDTSR if the following two constraints are satisfied

(i) There are a set of inconsecutive intervals, and the length of each interstice is not smaller thanτP,where the positive scalarτPis called the persistent dwell-time. This type of interval is called theτ-portion, where the switching signalϑ(m)is constant.

(ii)The above-mentioned interstices in(i)are divided by intervals whose length is no longer thanTP,where the positive scalarTPis called the period of persistence. This interstice is calledT-portion,on which signalϑ(m)can take different values.

Remark 3 The state estimator was designed for discretetime MJNNs with TPs subject to the ADTSR in Ref. [22].Compared with the DT and ADTSR, the PDTSR is more general. However, when it comes to TPs complied with the PDTSR,some researcher have studied this issue.As well summarized in one study in Ref.[34],we can obtain

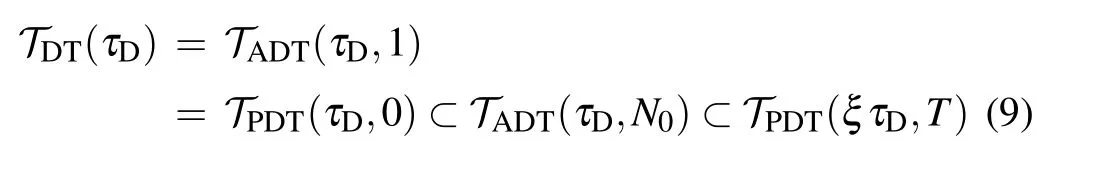
with∀τD＞0,∀N0≥1,ξ ∈(0,1) andT≜ξτD(N0−ξ)/(1−ξ). Then,TDT(τD),TADT(τD,N0) andTPDT(ξτD,T) represent the sets of switching signals with DT, ADT and PDT properties, respectively. Then, the DT and ADTSR can be regarded as special cases of the PDTSR.Therefore,the PDTSR is more flexible.

From Fig.1,there are two portions in thedth stage of the PDT switching signal:T-portion andτ-portion. Inτ-portion,the actual lengthτ(d)satisfiesτ(d)≥τP,and inT-portion,the actual length can be represented as T(d)=T(m)+···+T(o)+T(r)and meets T(d)≤TP. Heremqd,mqd+1,...,mqd+1−1,mqd+1denote the switching instants. For switching signalϑ(m)and an aleatoric section[l,k),the following inequality can be derived from Ref.[31]:

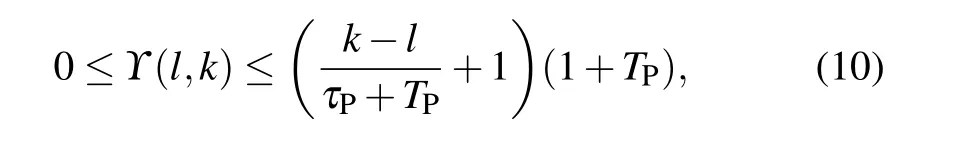
whereϒ(l,k)denotes the switching number within the interval[l,k).

Fig.1. The possible variations of the Lyapunov function under the consideration of the Markov chain with TPs subject to the PDTSR.

Remark 4 As the illustration in Fig.1,the Markov chain with piecewise constant TPs is used to depict the stochastic jumping of system modes. As for the PDTSR, inτ-portion,switching signalϑ(m)takes the same value, which is called slow switching. In T-portion, switching signalϑ(m)can arbitrarily switch among subsystems called fast switching. Thus,the PDTSR can effectively model switched systems with fast and slow switching characteristics. Then,mqdandmqd+1represent the sample and switching instants, respectively. In addition,the value of the Lyapunov function can increase or decrease at switching instants, but it is required to attenuate at sampling instants.

3. Main results

In this part,the goal is to study the stability for EES(3)inℋ∞sense. The following two theorems will provide some sufficient conditions,such that EES(3)is MSES with anℋ∞performance attenuation level. Then,the desired estimator gains can be obtained based on the proposed conditions.

3.1. Stability and performance analysis

Theorem 1 Given scalarsTP＞0,τP＞0,σ ＞0, 0＜κ1＜κ2, the change ratesr1∈(0,1),r2∈(1,∞), if there exists the Lyapunov functionV(ς(m),δ(m),ϑ(m)), such that for∀δ(m)∈ℳ,∀ϑ(m)∈J,the following inequalities hold:

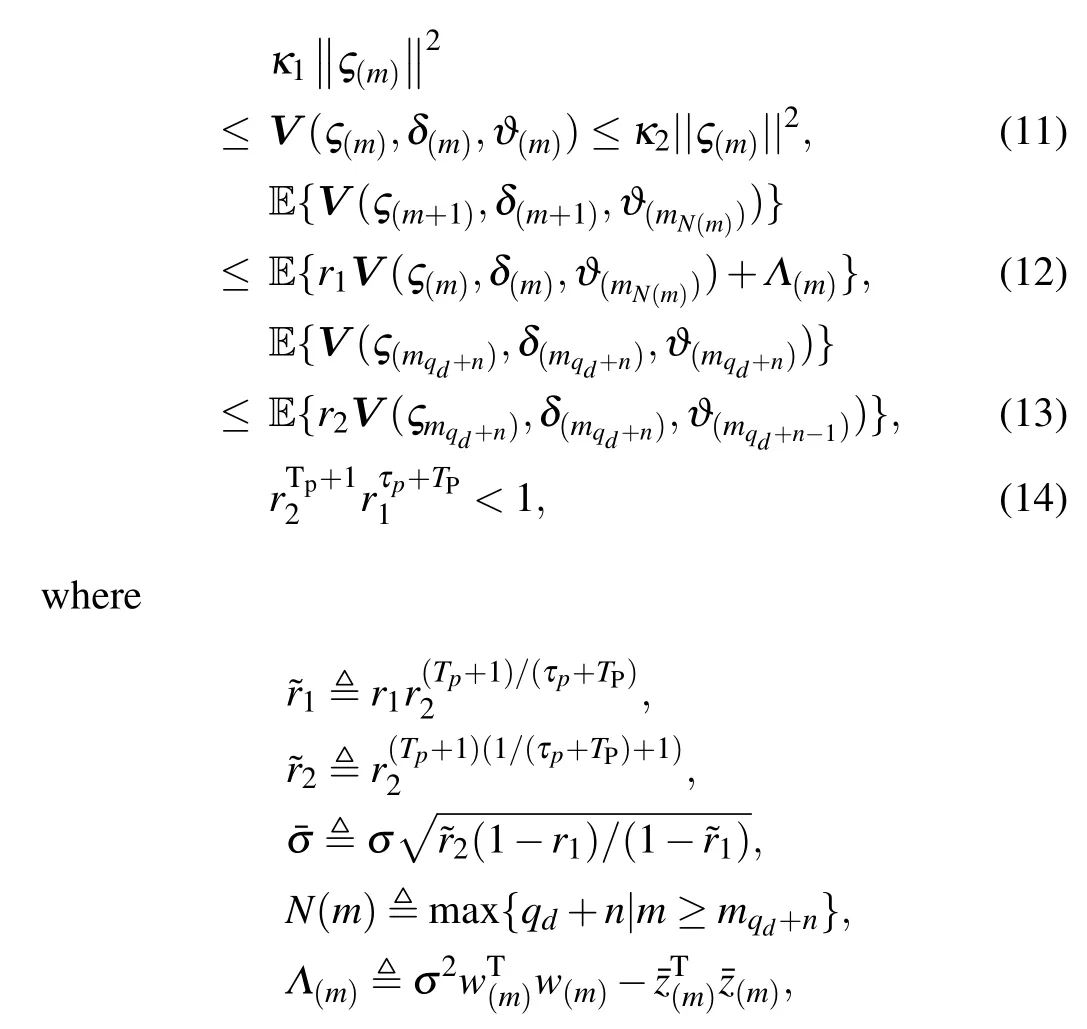
then EES (3) is MSES with anℋ∞performance attenuation level.

Proof

Step 1 The following relationship can be obtained from Eq.(12)in the case ofw(m)≡0:

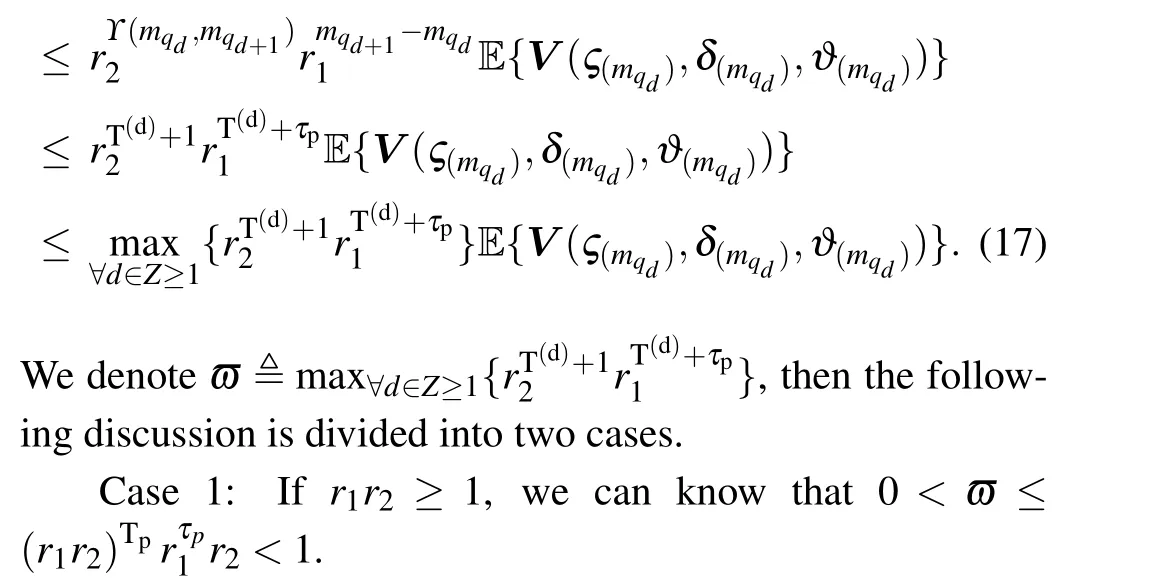
Case 2: If 0＜r1r2＜1,one can deduce 0＜ϖ ＜1.

Therefore,inequality 0＜ϖ ＜1 hold for anyr2∈(1,∞)andr1∈(0,1).

It follows Eq.(17)that

Denotingm0≜mq1,it is deduced that

Step 2 Settingm ∈[mqd,mqd+1), from inequality (10),one can obtain the following inequality according to Eqs.(12)and(13):

Considering zero-initial conditions,we can deduce that

Thus, it can be seen from Eq. (5) that EES (3) is MSES with anℋ∞performance attenuation level.

Remark 5 Note that we consider that 0＜r1＜1 andr2＞1 are the changing rates at the sampling instants and the switching instants, respectively. Here 0＜r1＜1 means that the Lyapunov function is attenuated at sampling instants;r2＞1 denotes that the Lyapunov function can rise at switching instants. Different from the limitation that the Lyapunov function is attenuating over the entire period.In this study,the Lyapunov function is permitted to increase at switching instants as long as the overall function value represents a declining trend.There is still huge research potential to investigate the change of Lyapunov function,which can guarantee the stability of the systems along with less conservatism.

3.2. Estimator design

Based on Theorem 1,the parameters of the state estimator are developed below.

Theorem 2 Considering EES (3), for given scalarsr2∈(1,∞),r1∈(0,1),σ ＞0, andυ ∈(0,∞), if there existΓi ＞0(∀i ∈ℳ) and symmetric positive definite matricesPθi(∀i ∈ℳ,θ ∈J) satisfying Eq. (14), and the following conditions hold for∀i ∈ℳ,∀θ ∈J:

then, EES (3) is MSES with anℋ∞performance attenuation level. Furthermore, the desired estimation gains can be obtained asKi.

Proof Settingδ(m)≜i,ϑ(m)≜θ,i ∈ℳ,θ ∈J, the Lyapunov function for EES(3)is constructed as

one can derive that

where

Then,criterion(11)is guaranteed.

For∀υ ∈(0,∞),the following derivation is satisfied,

It can be obtained from Eq.(12)that

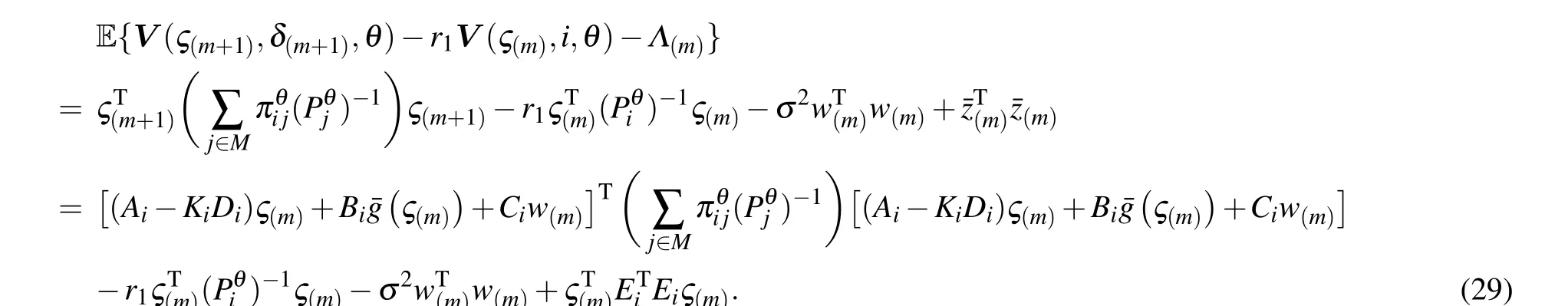
Furthermore,it follows from Eq.(29)that

where

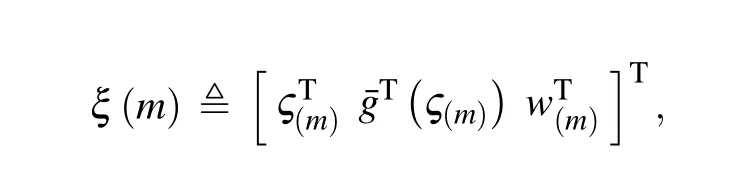
Then, by using Schur complement, it can be obtained from Eq.(27)thatΘ ＜0. Therefore,formula(12)is satisfied.

On the other hand,from condition(27),and for∀i ∈ℳ,∀θ1,θ2∈J,we have

Therefore,based on Eq.(31),inequality(13)is satisfied.This ends the proof.

4. Numerical simulation

In this section, MJNNs with TPs subject to the PDTSR are presented to substantiate the validity of the proposed state estimator.

We consider the discrete-time MJNNs with two modes.

Mode 1

whereg1(x1(m))=tanh(x1(m)),g2(x2(m))=tanh(x2(m)). According to Lemma 1, we get matricesΦ−= 0, andΦ+=diag{0.5,0.5}, and the exogenous disturbancew(m)=10exp(−0.06m)sin(0.5m).

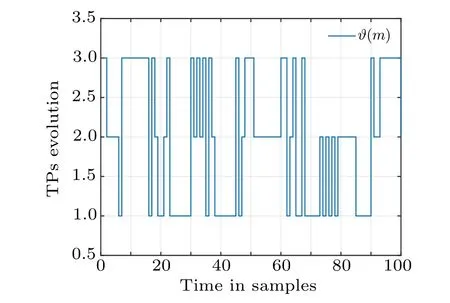
Fig.2. The evolution sequence of the switching signal ϑ(m).

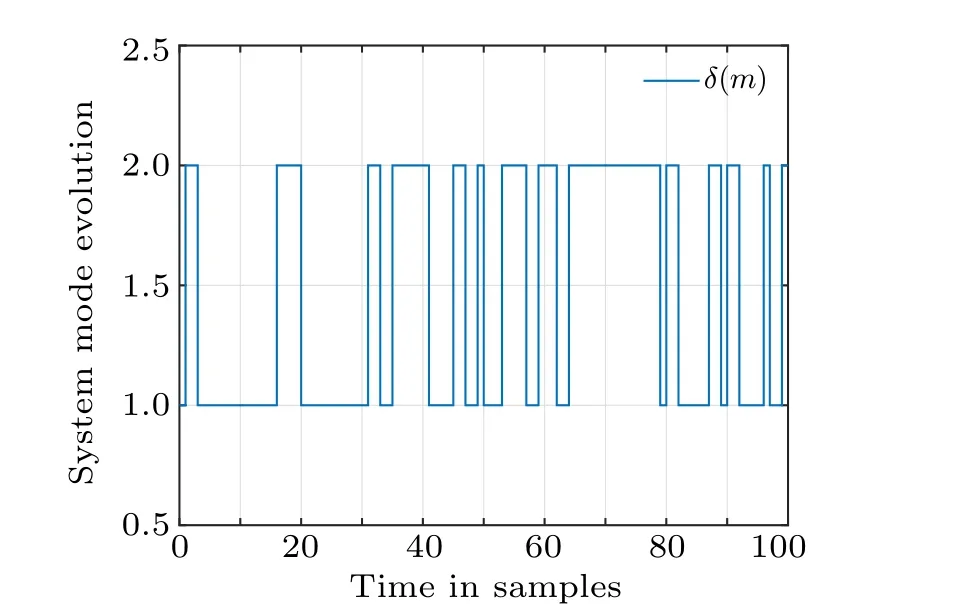
Fig.3. The evolution sequence of the jumping signal δ(m).

The parameters of the Markov chain are given as follows:

Moreover,the parameters related to the PDTSR are given as

Then,based on Theorem 2,σ=1.2,andυ=1,the state estimator gains can be presented as follows:

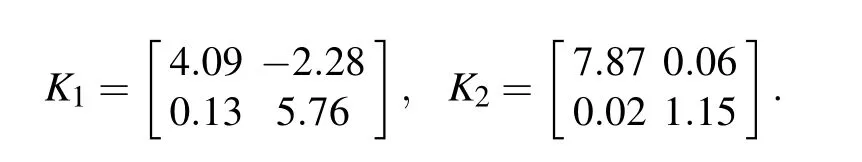
Fig.4. The state responses of system state and estimate state.

Fig.5. The responses of the estimation error.

Fig.6. Optimal values of min with different r1 and r2.

Consider that the initial states are selected asx(0)=[1.48 1.6]T,(0)= [0 0]T. Then, the state responses of the researched system and the estimator are presented in Fig. 4.Then,the responses of the EES are drawn in Fig.5. The goal of this study is to construct a mode-dependent state estimator for MJNNs with TPs subject to the PDTSR,such that EES(3) is mean-square exponentially stable and has a prescribedℋ∞performance index. Firstly, the evolution of TPs satisfying the PDTSR is displayed in Fig. 2, and the Markov chain used is in Fig. 3, respectively. Then, Fig. 5 shows that the state responses of EES(3),from which it can be seen that the proposed mode-depended state estimator is indeed effective.By applying the obtained estimator gains, the state responses of the researched system and the estimator are presented in Fig.4,which demonstrates that the designed estimator can effectively track the states of discrete-time MJNNs in the case that the time-varying TPs are subject to the PDTSR.Furthermore,the relationship betweenminandr1,r2can be obtained through the dichotomy method. As shown in Table 1,and the trend of the above relationship is presented in Fig.6. We can find that the decay rater1at sampling instants and the change rater2at switching instants have impact on the system performance index to some degree. Thus, choosing an appropriate Lyapunov function change rate to sure the prescribed performance index of the desired system is important.

Table 1. Optimal H∞performance index min for different values of r1 and r2.

Table 1. Optimal H∞performance index min for different values of r1 and r2.

¯σmin r2=1.12 r2=1.14 r2=1.16 r2=1.18 r2=1.2 r2=1.22 r1=0.74 0.3109 0.3464 0.3858 0.4295 0.4780 0.5319 r1=0.78 0.3203 0.3598 0.4042 0.4543 0.5112 0.5760 r1=0.82 0.3370 0.3838 0.4382 0.5021 0.5780 0.6696 r1=0.86 0.3714 0.4364 0.5189 0.6276 0.7802 1.0190

5. Conclusion

In this work, the issue ofℋ∞state estimation has been discussed for a set of discrete-time Markov jump neural networks. In this framework, the change of the piecewise timevarying transition probabilities of the Markov chain, which governs the evolution of TPs, is subject to the switching signal with the persistent dwell-time switching property. Moreover, some sufficient conditions have been established such that the error estimation system is stable with anℋ∞performance index. Finally, an illustrated example has been provided to show the effectiveness of the designed state estimator and the feasibility of the proposed method. As for piecewise time-varying transition probabilities subject to the persistent dwell-time switching rule, future work may extend the obtained results to more complex Markov jump neural networks.