Effect of symmetrical frequency chirp on pair production∗
Kun Wang(王焜) Xuehua Hu(胡学华) Sayipjamal Dulat and Bai-Song Xie(谢柏松)
1School of Physics and Technology,Xinjiang University,Urumqi 830046,China
2Key Laboratory of Beam Technology of the Ministry of Education,and College of Nuclear Science and Technology,Beijing Normal University,Beijing 100875,China
3Beijing Radiation Center,Beijing 100875,China
Keywords: pair production,Dirac–Heisenberg–Wigner formalism,symmetrical frequency chirp
1. Introduction
At the beginning of its establishment,quantum electrodynamics theoretically predicted that vacuum would decay and produce electron–positron pairs in strong electric fields,which is called as the Sauter–Schwinger effect.[1–3]However, the current laser intensity (about 1022W/cm2) is still far lower than the laser intensity corresponding to the critical field intensity (about 1029W/cm2), so it has not been verified by experiments.[4]However,with the rapid development of laser technology and the increasing intensity of electric fields, the generation of pair in the vacuum is expected to be confirmed by experiments soon. For recent research progress,please refer to Refs.[5,6].
At present, it is a consensus that only the Schwinger tunneling mechanism cannot generate observable electronpositron pair. Therefore, people have proposed another mechanism, multiphoton pair generation, which can generate electron–positron pair in a vacuum by absorbing several high-energy photons.[7,8]In addition, to overcome the limitation that the current laser equipment does not provide enough high-energy photons to make observable pair,several catalytic mechanisms for the generation of observable pair under subcritical conditions are proposed.For example,the dynamically assisted Schwinger mechanism[9–11]can effectively combine the above two pair generation mechanisms, thus significantly increasing the pair production. Another method to enhance the number density of pair is to use the electric field with frequency chirp,[12–15]a scheme called chirped pulse amplification was proposed by Strickland and Mourou[16]in the early 1980s which generates intense laser pulses without destroying the amplification medium. Moreover,the technique is also used to obtain the existing high-power laser.When it is applied to the theoretical study of the Sauter–Schwinger effect,proper chirp parameters can increase the number density of particles produced by several orders of magnitude.[13–15]
Here, we report our study about the effect of using the electric field with symmetrical frequency chirp on pair production using frequency chirp signals. We consider the relationship between the number density and the symmetrical frequency chirp signal that varies with time, and then compare the result with the asymmetrical frequency chirp to analyze the difference. In addition,we conduct a quantitative analysis of the momentum spectrum and give qualitative explanations,which also provides new ideas for the experiment.
This paper is organized as follows. In Section 2, we briefly introduce the Dirac–Heisenberg–Wigner (DHW) formalism. In Section 3, we present the electric field form. In Section 4, we present the numerical results for different polarization parameters and different chirp parameters,and momentum spectra with different frequency chirp parameters and four different types of polarization. In the last section, we present our conclusions.
2. The DHW formalism
In this paper, we use the DHW formalism which is suitable for pair production.[17–23]In the following, we briefly review the DHW formalism, which begins with the gaugeinvariant density operator

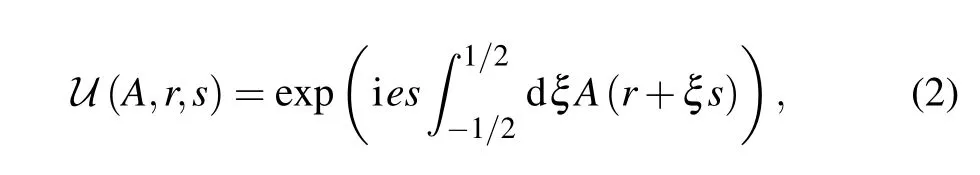
which is added for ensuring that the density operator is gaugeinvariant and only related to the background gauge fieldAand elementary chargee.[24]Note that the background field is treated in mean-field (Hartree) approximation,Fµν(x)≈〈µν(x)〉.
The Wigner operator

which involves the electron’s quantum fluctuations. Then,the covariant Wigner function can be generated by the vacuum expected value of the Wigner operator obtained above,

For the accurate representation of matter dynamics in 3+1 dimensions and the convenience of numerical calculations, the covariant Wigner function can be converted to a combination of the Dirac gamma matrix. So we can decompose it into 16 covariant Wigner components

where the sixteen components S, P, Vµ, Aµ, and Tµνare scalar, pseudoscalar, vector, axial vector, and tensor, respectively. Using an equal-time approach[25]to further simplify,the individual Wigner components can be written as)

Similarly, the 16 components can also be deduced separately,which are too long to list them,and the specific derivation can be found in Refs.[18,26]. Meanwhile,because of the non-local nature of the pseudo-differential operators, solving their numerical solutions is very challenging.[20,26–28]For the homogeneous electric field(13),we can choose vacuum initial conditions as starting values. The non-vanishing values are

wheremis the mass of an electron. Therefore, sixteen Wigner components can be simplified into ordinary differential equations,[22]and ten of them are non-vanishing,

And the one-particle distribution function can be defined as

Then, by solving the distribution functionf(qqq,t) and ten ordinary differential equations, the following equations can be derived:

With initial conditionsf(qqq,−∞)=0,vvv(qqq,−∞)=aaa(qqq,−∞)=ttt(qqq,−∞)=0,the density of the number of pair creation can be obtained by calculating the integral of the distribution function in the momentum space at timet →+∞,
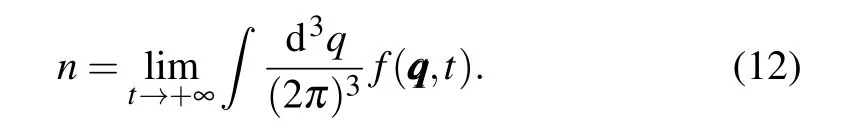
3. The external field form
In this section, we establish the following electric field form in order to study the symmetrical frequency chirp:



Fig. 1. The electric field E(t) varies with time in linear polarization(δ =0). The parameters are chosen as E0=0.1Ecr,ω =0.6m,and τ =10/m,where m is the electron mass. The blue solid line represents the electric field without the chirp parameter b=0. The red dashed line stands for the field with the chirp parameter b=0.005 m2,the dark solid line shows the electric field with the chirp parameter b=0.06 m2.
In terms of experiments, due to the limitations of the instrument, producing a perfect circular polarization field is much more difficult than an elliptical polarization field, for instance, the polarization of the experimental laser field is as high as 0.93.[30]Therefore,we include the numerical calculation of a near-circular elliptical polarization. Besides three of the parameters of the electric field(13)are fixed as

The form of Keldysh adiabatic parameter isγ=mω/eE,and multiphoton pair effect and Schwinger(tunnel)effect are determined byγ ≫1 andγ ≪1, respectively.[31]Therefore,for the known equation(14),not only the influence of the polarization parameterδon the Keldysh adiabatic parameterγshould be considered, but also the frequencyωwill change into the effective frequency when the chirp parameterbis not zero. For the chirp parameterb,we research several situations where the interval is 0≤b ≤0.06m2and choose four different values ofδaccording to the polarization state. And we clearly know that the pulse length in this paper is not enough to get a pure multiphoton signal, and for the chirp parameterb=0.06m2,its value is beyond the scope of“normal chirp”.However, the current exploratory research goal is to qualitatively understand the influence of the symmetrical frequency chirp on the number density and momentum spectra with different types of polarization and compare with known results.

Fig.2. The Fourier transform of the electric field with the asymmetry chirp and the symmetry chirp. The other parameters are consistent with those in Fig.1. Two pictures in the upper left, the upper right, in the lower left, and the lower right use asymmetrical chirp and symmetrical chirp at b=0.001,b=0.009,b=0.03,and b=0.06,respectively.
To explain the following numerical results, we use Fourier transform of the electric field(13),as shown in Fig.2.With the increase of the chirp parameterb, the frequency spectra of the electric field with the asymmetrical and symmetrical chirped pulses gradually show a multi-peak structure, and the main peak shifts. Specifically speaking, the main peak of the asymmetrical pulsed electric field gradually moves to the high frequency with the increase ofb,while the main peak of the field with symmetrical frequency chirp moves to the direction of zero frequency. At the same time, both the symmetrical electric field and the asymmetrical electric field have the dynamically assisted Sauter–Schwinger mechanism.[9–11]Specifically speaking,the asymmetrical electric field can be regarded as a low-frequency strong field at first, and then a high-frequency weak field;while,the symmetrical electric field is a high-frequency weak field at first, then a low-frequency strong field, and finally a high-frequency weak field. Both of the above combinations accord with the basic condition of dynamically assisted Sauter–Schwinger mechanism.[9–11]What is more, for the symmetrical chirp, the mechanism is more obvious and intuitive. Besides, we will quantitatively explain the formation of the peaks in the momentum spectrum by considering the Fourier transform of the electric field in Subsection 4.2.
4. Numerical results
In this section,we show the main results of particle number density under different symmetrical chirp parameters and different polarizations and the momentum spectra in the linearly polarized field.
4.1. Pair number density
In this subsection,we study the number density of the created electron–positron pairs in different polarizations or different chirp parameters. In Fig.3,we show the change of the number density with the polarization parameterδ. The expected symmetry can be seen when mirroringδ →−δ. More specifically,we observe the following from Fig.3. First,whenbis small(b <0.01m2),the curves corresponding to differentbvalues are similar and the relative difference of the number density for different polarizations is large;whenbis large(b >0.01m2),the similarity disappears and the relative difference becomes smaller. And,with the increasing chirp parameterb, the peak value of the positron–electron number density also increases significantly. Especially, whenbincreases from 0.02m2to 0.03m2, the number density has been expanded around 15.96 times. Meanwhile, the difference between the number densities of the symmetrical electric field and the asymmetrical electric field is proportional tob. The corresponding numbers are provided in Table 1.
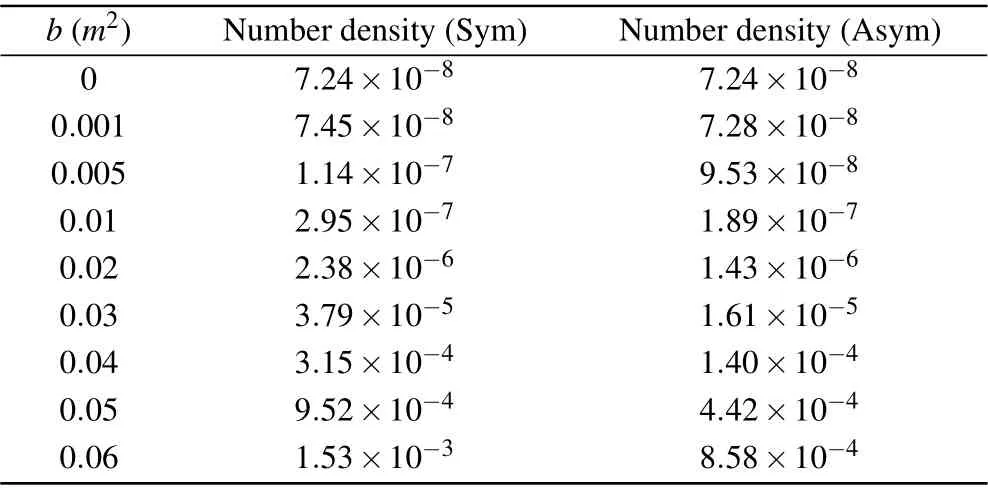
Table 1. Numerical results for the number densities(in units of λc− 3=m3)for circular polarization and some selected chirp parameters in Fig. 4 (in units of m2).

Fig. 3. The number density of the pair production varies with the polarization parameter δ, for the different symmetrical chirp parameter b.The other parameters are the same as those in Fig.1.
In Fig.4,firstly,the number density has been further improved compared with that of the asymmetrical chirp,and the changing trend is consistent. Secondly, whenb ≤0.018m2,the number density of linear polarization is significantly higher than that of elliptical polarization and that of circular polarization. But whenb ≥0.018m2, the curves of these three polarizations have the same changing trend, and the difference among them is almost indistinguishable (when the chirp parameterbis the same,the relative error does not exceed 0.1).The phenomenon has been discussed in the reference[32]that the number density produced by linear polarization is occasionally lower than that of circular polarization and elliptical polarization with the increase of the chirp parameterb.
The most notable phenomenon in Fig.4 is that the difference between the number density for symmetrical chirp and that for asymmetrical chirp becomes bigger when the chirp parameterbincreases. The reason is that the increase in frequency chirp not only causes the increasing in the Keldysh adiabatic parameterγ, but also makes multiphoton pair production gradually dominate.According to Fig.2,we can make a reasonable explanation,when the electric field with symmetrical chirp has a small chirp parameter(b <0.01m2),the dynamically assisted Sauter–Schwinger mechanism[9–11]is not obvious, and the pair generation is dominated by the field strength. So it can be explained in Fig.4 that when the chirp parameterbis small(b <0.01m2),the number density in this paper is a little different from the number density with asymmetrical chirp. On the contrary,when the symmetrical chirped electric field has a large chirp parameter (b >0.01m2), the effective frequency of the electric field is large and the generation of vacuum electron–positron pair should be dominated by multiphoton pair generation process, and the frequency of the symmetrical chirped electric field becomes higher in the parts oft >0 andt >0,which means the dynamically assisted Sauter–Schwinger mechanism[9–11]becomes intense.

Fig. 4. The number density of the pair production varies with the chirp parameter b for the different polarization parameters δ =0(LP),δ =0.5 (EP), and δ =1 (CP). “Sym” and “Asym” represent the field with symmetrical chirp and with asymmetrical chirp,respectively. The other parameters are the same as those in Fig.1.
We observe that the step-like distortion in Fig. 4 appears, which maybe due to the dynamically assisted Sauter–Schwinger mechanism.[9–11]In the vicinity of certain specific chirp values,the effect will be enhanced,which maybe needs further exploration in the future.
4.2. Momentum spectra
In this subsection, we present our results about the momentum spectra in the linearly polarized field (δ=0). The elliptically polarized field(δ=0.5),circularly polarized field(δ= 1.0), and near-circularly polarized field (δ= 0.9) are shown in Appendix A.In the case of linear polarization(δ=0),the electric field is oriented only along thex-axis,therefore the momentum spectra have rotational symmetry around theqx-axis,as plotted in Fig.5.In the case of no chirp(b=0),our result is consistent with the results of the references.[15,33]For the non-zero (b/=0) chirp parameter, the main result is that except the symmetry of the momentum spectra, some strong interference effects also appear, which eventually lead to that the momentum spectra of e+e−pair tend to have multiple concentric ring structure.
More specifically,firstly,forb=0,the main peak region of the momentum spectra evenly distributes at the center,and the momentum spectra are symmetrically distributed inqxandqyplanes. Secondly, by comparing the momentum spectrum for non-chirp with the momentum spectra for the chirp parametersb=0.002m2,b=0.005m2,andb=0.009m2,we find that the shape of momentum spectra changes slightly with the small chirp parameters (b <0.01m2), but the peak value of the momentum spectra improves significantly(when the chirp parameter increases fromb=0 tob=0.009m2, the center value of the momentum spectra is enlarged by 3.458 times).Thirdly, when the chirp parameter changes fromb=0.0 tob=0.002m2, the four small peaks around the central region cannot be observed,and the maximum value of the central region is more than doubled.Fourthly,when the chirp parameter increases tob=0.005m2,the overall shape of the momentum spectra is an elliptical structure,and the distribution range(red and green regions)becomes larger.Finally,when the chirp parameter increases tob=0.009m2,the momentum spectrum is still mainly distributed in the center,and further expanded.
For larger frequency chirp (b ≥0.01m2), some more complex structures are found in the momentum spectra: the entire momentum spectra have changed significantly,and they are mainly distributed on both sides of the symmetry center,as shown in the lower panels of Fig. 5. Interestingly, whenb= 0.02m2, the momentum spectrum is divided into two identical main peak regions and two identical sub-main peak regions which are symmetrically distributed on both sides of the center. Whenbincreases to 0.03m2, the main peak regions (red) of the momentum spectra on both sides move to the center and merge,and the sub-peak regions(green)of the momentum spectra also move to the center, refer to Fig. 6.In the above case, since the chirp parameterbof the electric field easily changes the distribution of the turning points on the complex time plane,it is found that the phenomenon is caused by the interference between multiple pairs of the main turning points.[34]
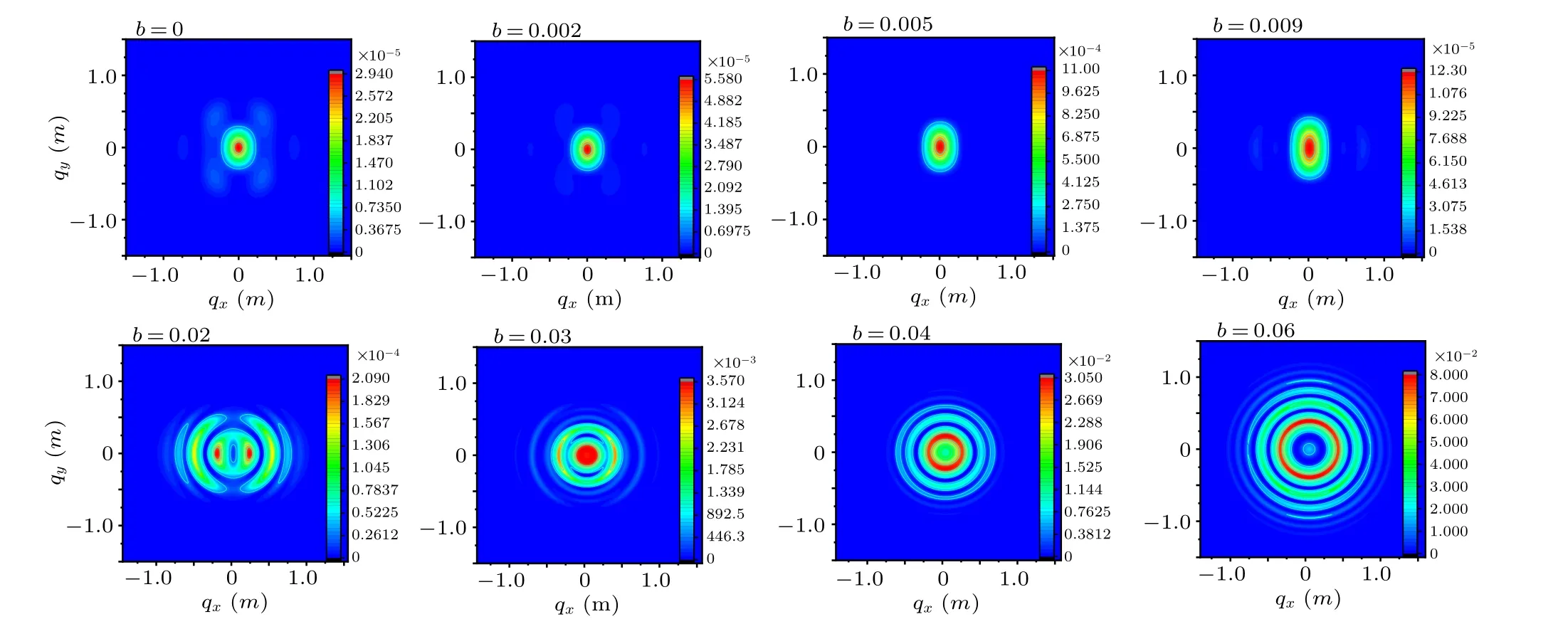
Fig. 5. Momentum spectra of e+e−pair production for linearly polarized field (δ =0) in the (qx,qy)-plane and with qz =0. The other parameters are the same as those in Fig.1. Upper row: the small chirp parameters b=0,0.002 m2,0.005 m2,and 0.009 m2. Bottom row: the large chirp parameters b=0.02 m2,0.03 m2,0.04 m2,and 0.06 m2.

Fig. 6. Momentum spectra of pair production for linearly polarized field(δ =0)at qy=qz=0,cf. Fig.5.
Whenb=0.04,the main peak(red)region of the momentum spectrum is ring-shaped and evenly distributed around the center of symmetry. Whenb=0.06m2,the main peak region of the momentum spectrum expands away from the center of symmetry, and the torus-like region becomes narrower. As the chirp parameter increases, a ring structure affected by interference effects appears. Because the quantum interference effect between the amplitudes of the electric field is related to the cycle number of the electric field during the e+e−pair generation.[35]In addition, e+e−pair generation in the vacuum is a typical non-Markovian process, which means that the evolution of the number density of e+e−pair over time depends on the complete earlier history. Therefore, small changes of various parameters contained in the strong background field usually significantly change the relative phases of the amplitudes.[14]Whenb=0.06m2, the momentum spectrum shows a regular diffraction pattern.
The result of the symmetrical chirp field is the same as expected: the overall momentum spectrum shape is symmetrical aboutqxandqy. And the momentum spectrum has been uniformly distributed around the center of symmetry during the evolution process,which is different from the electric field with asymmetrical chirp.[15]In the momentum spectrum aboutqxin Fig. 6, the peak of the momentum spectrum is located atqx=0 for non-chirp. With the chirp parameterbincreasing, the peak of the momentum spectra will slightly move to the positiveqxdirection,and the overall momentum spectrum maintains symmetry. Forb=0.02m2, we can not only see four significant maximums but also other less obvious maximums. Lastly, the maximum value of the momentum spectra is proportional to the chirp parameterb.
Next is our quantitative analysis. From the conservation of energy generated by multiphoton pairs, we get the general relationship


Combining the results in Appendix A,one obtains some detailed information about the momentum spectrum. It can be found that the momentum spectra are very sensitive to the frequency chirp parameterb, which includes the deformation of the ring structure, the appearance of interference effects,and the significant increasing of the single-particle distribution function. For example, in all the cases considered, it is more common that when the frequency chirp parameter increases,the peak value of the momentum spectra will increase strongly. It is easy to understand when the frequency chirp parameterbincreases, the effective frequency of the strong field (ωeff=ω+b|t|) will also increases which means the probability of the multiphoton pair generation process will increase. In other words, if a strong field has a constant frequency(ω=0.6m)and a large frequency chirp,it will contain higher frequency components,so the probability of e+e−pair generation will increase. Also, the momentum spectra verify the existence of the dynamically assisted Sauter–Schwinger mechanism[9–11]mentioned above. During the duration of the symmetrically chirped pulse,the“early-time”and“late-time”of the field are also similar to an almost pure multiphoton signal,so e+e−pair generation under large chirp parameters is dominated by the multiphoton pair production mechanism.And in different polarizations, with the chirp parameterbincreasing,the momentum spectrum shows more and more ring structures,which is created by multiphoton.
5. Summary
Within the DHW formalism, we studied pair production in the four different types of polarized electric fields with symmetrical frequency chirp and compared it with that in the electric field with asymmetrical frequency chirp. The main results of the number density and spectrum of e+e−pair,which are generated in the arbitrary polarized electric fields with the symmetrical frequency chirp,are summarized as follows.
Both the differences between the fields with the symmetrical frequency chirp and with the asymmetrical frequency chirp similarly have an effect of the dynamically assisted Sauter–Schwinger mechanism,[9–11]but the composition of the former is a high-frequency weak field at first, then a lowfrequency strong field,and finally a high-frequency weak field.And its high-frequency components are more than those of the asymmetrical pulse chirp electric field.Therefore,for different polarizations, with the increase ofb, the difference between the number density of the symmetrical chirp and that of the asymmetrical chirp also increases. The specific numerical values are given in Table 1. In addition,with the increase of the chirp parameter, the number density of linear polarization is occasionally lower than that of circular polarization and elliptical polarization when the other parameters are the same.
Moreover, for the linearly polarized electric field, with the increase of the chirp parameterb, the momentum spectra of e+e−pair production exhibit peak expansion and splitting and strong interference effects.There is no doubt that the most complex change in the momentum spectra occurs in the elliptical polarization. For elliptical polarization,near-circular elliptical polarization,and circular polarization,it is found that the main peak region of the momentum spectra will move along the direction ofqywith the increase of the chirp parameterb.We think the reason for that is the electric field form in this paper. Specifically speaking, for the polarization parameterδ=0(linear polarization),there is no influence of the electric field iny-axisEy; whenδ=0.5 (elliptical polarization), the influence ofEyappears.Eycan not only increase the particle number density but also be equivalent to an accelerating electric field. Whenδ=1.0(circular polarization), the influence ofEyis more significant,and the main peak region also has a more obvious oscillation.
However, the most important discovery is that the electric field with symmetrical frequency chirp can clearly reflect the existence of the dynamically assisted Sauter–Schwinger mechanism.[9–11]When the chirp parameterbincreases, the momentum spectra of arbitrary polarization will eventually tend to a concentric ring structure,which is caused by the multiphoton process. Because large frequency chirp can provide a lot of higher frequency components, the “early-time” and“late-time”of the duration of the symmetrically chirped pulse are similar to an almost pure multiphoton signal.
In the study, the external laser pulse is limited to a very high electric field intensity and last very short. For a possible explanation for increasing the number of pairs production in terms of multiphoton pair production,a longer pulse study will be necessary.Considering the dramatic increase of the number density and the associated improved experimental observation potential, it is certainly feasible to use smaller electric field values and longer pulse times for research.
Acknowledgement
Authors are grateful to Dr. O. Olugh for helpful discussions.
Appendix A:Momentum spectra
A1: Elliptically polarized field δ =0.5
For the elliptical polarization (δ=0.5), the momentum spectra are shown in Fig. A1. On the whole, the momentum spectrum has reflection symmetry. When the chirp parameterbis small(such as the first row of Fig.A1),the overall change is relatively mild.More specifically,the overall graph expands away from the center of symmetry, and ring structures gradually appear. When the chirp parameterbis large (such as the lower row of pictures in Fig.A1), the momentum spectra will be quite complicated reordering, which is similar to the linear polarization situation. More specifically, a single extreme value splits into several maxima at first,and then a ring structure gradually appears. Especially forb=0.06m2,a ring structure similar to linear polarization appears,and the overall range is expanded. Meanwhile, its peak value has been enhanced by four orders of magnitude,from 9.65×10−6(whenb=0)to 8.1×10−2(whenb=0.06m2).

Fig.A1. Momentum spectra of e+e−pair production for elliptically polarized field(δ =0.5)in the(qx,qy)-plane and with qz=0. The other parameters are the same as those in Fig.1. Upper row: the small chirp parameters b=0,0.002 m2,0.005 m2,and 0.009 m2. Bottom row: the large chirp parameters b=0.02 m2,0.03 m2,0.04 m2,and 0.06 m2.
A2: Circularly polarized field δ =1.0
For the circular polarization (δ= 1), the momentum distribution of e+e−pair is shown in Fig. A2. When the chirp parameterb=0,the momentum spectrum shows a ring structure centered at the origin, the weak interference effect, and the oscillation between the hole and the outer ring.These phenomena can be also found in references[21,33,35]and explained by the effective scattering potential in the semiclassical analysis.[15,34]The radius of the ring in momentum spectra can determine the total number of photons used to produce e+e−pair, by considering the effective mass formula of e+e−pair generation according to the energy conservation.[37]

Fig.A2. Momentum spectra of e+e−pair production for circularly polarized field(δ =1) in the (qx,qy)-plane and with qz =0. The other parameters are the same as those in Fig.1. Upper row: the small chirp parameters b=0,0.002 m2,0.005 m2,and 0.009 m2. Bottom row: the large chirp parameters b=0.02 m2,0.03 m2,0.04 m2,and 0.06 m2.
Note that the peak value of the momentum spectra increases significantly as the frequency chirpbincreases, and the main peak region(red)of the momentum spectrum has the oscillation phenomenon. The main peak region (red) of the momentum spectrum is evenly distributed around the center of symmetry forb=0. As the chirp parameterbincreases,the main peak region moves toward the negativepydirection firstly and then toward the positivepydirection, and finally,tends to uniform when the chirp parameterb=0.04m2. The reason for the oscillation phenomenon is the electric field we used,in whichExis symmetrical about the time axis,and theEyaxis is symmetrical about the origin. More specifically,whenδ=0 (linear polarization), there is no influence ofEy.And forδ=0.5 (elliptical polarization), the influence ofEyappears. Meanwhile,Eycan not only increases the pair generation,but the remainingEycan also be regarded as an accelerating electric field, which can accelerate the generated e+e−pair. Consequently,forδ=1.0(circular polarization),the influence ofEyis more significant, and with the increasing of the chirp parameterb, the central value also fluctuates more significantly.
A3: Near-circularly polarized field δ =0.9
The characteristic shape of the momentum spectrum may be helpful for the experimental identification of the vacuum e+e−pair generation under a strong field. Therefore,the momentum spectrum of the near-circular elliptical polarization(δ=0.9)is calculated,in Fig.A3. These results are similar to the results of helium ionization in strong-field[38]and the pair production in an electric field with different polarizations.[35]Under a relatively small chirp parameter (b ≤0.01m2), We can also see the violent effect of chirp. On the other hand,for a large chirp parameter(b ≤0.01m2), similar to the evolution of circular polarization and elliptical polarization discussed earlier: the momentum spectrum loses the symmetry in the direction ofqyand finally tends to the structure of concentric rings.

Fig.A3. Momentum spectra of e+e−pair production for near-circularly polarized field(δ =0.9)in the(qx,qy)-plane and with qz =0. The other parameters are the same as those in Fig.1. Upper row: the small chirp parameters b=0,0.002 m2,0.005 m2,and 0.009 m2. Bottom row:the large chirp parameters b=0.02 m2,0.03 m2,0.04 m2,and 0.06 m2.
- Chinese Physics B的其它文章
- Quantum computation and simulation with vibrational modes of trapped ions
- ℋ∞state estimation for Markov jump neural networks with transition probabilities subject to the persistent dwell-time switching rule∗
- Entanglement properties of GHZ and W superposition state and its decayed states∗
- Lie transformation on shortcut to adiabaticity in parametric driving quantum systems∗
- Controlled quantum teleportation of an unknown single-qutrit state in noisy channels with memory∗
- Continuous-variable quantum key distribution based on photon addition operation∗

