Entanglement properties of GHZ and W superposition state and its decayed states∗

Xin-Feng Jin(金鑫锋), Li-Zhen Jiang(蒋丽珍), and Xiao-Yu Chen(陈小余)

College of Information and Electronic Engineering,Zhejiang Gongshang University,Hangzhou 310018,China

Keywords: quantum entanglement,Wootters formula,matched entanglement witness,coherence

1. Introduction

Quantum entanglement plays a crucial role in quantum information and quantum computation. Thus, judging whether a quantum state is entangled has become a prominent topic in quantum information. In Ref. [1] the entanglement property of the mixed state of three-qubit W state and GHZ state has been studied, and the superposition state has rarely been investigated. In this paper,we study the entanglement properties of the superposition of three-qubit GHZ state and W state and its decayed states.

Many entanglement criteria have been proposed for bipartite systems[2–6], such as PPT criterion,[7]which is necessary and sufficient for 2×2 and 2×3 bipartite systems to be separable, but it is no longer sufficient in the higher dimensions. Therefore, PPT criterion is often used as an auxiliary verification method. In multipartite systems,[8–13]there is no simple criterion. The entanglement witness (EW)[14–17]is a common method for entanglement detection of multipartite systems, and the construction of EW becomes a task for entanglement detection.

Another method for identifying entanglement is formulated in terms of Wootters formula. It is restricted to a twoqubit system,and its application in multipartite systems is limited. Thus the generalized Wootters formula was proposed,and it is not only applicable to higher dimensional bipartite systems but also to multipartite systems.

It is well known that both entanglement and coherence[18,19]originate from the superposition principle.Therefore, it is a very meaningful work to study the relationship between them.[20–24]

This paper has two purposes. Firstly,we use the the generalized Wootters formula, PPT criterion and matched entanglement witness, to detect entanglement of the superposition state of three-qubit GHZ state and W state and its decayed states. We find that the generalized Wootters formula can be used as a tight criterion for the full separability of quantum states near the W state. In the other parts, the PPT criterion is superior to the generalized Wootters formula. Secondly,we show the connection of entanglement and coherence for the above superposition state.

2. The generalized Wootters formula

The concurrence is a useful tool to characterize quantum correlations in various physical systems. Concurrence was first proposed by Wootters in 1998.[25]Wootters formula of a two-qubit stateρis

Whenp=1, the stateρG(p) is the pure GHZ state, we can obtain thatρG(p)is entangled whenp ＞1/5.

wherea2+b2=1. The above formula is further extended to cover the case of decaying,

wheregandware probabilities,τrepresents the decaying factor (the degree of decay), and its value ranges from 0 to 1.Whenτ=0,the state in Eq.(6)represents the mixed state of the three-qubit GHZ state and W state with white noise, and whenτ=1,it represents the superposition state of the threequbit GHZ state and the W state mixed with white noise.

By mixingJWandJGHZ, we obtainJ=αJW+βJGHZ,whereαandβare probabilities andα+β=1, its explicit form in computational basis is

3. Matched entanglement witness

The state (6) can also be decomposed with the products of Pauli matrices and the identity matrixσ0of 2×2,namely,

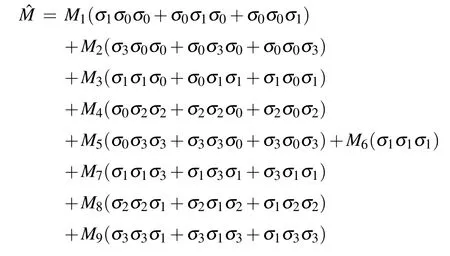
is minimized. While choosingMiwe keep bothΛandM·Rpositive,M ≡(M1,M2,...,M12). We have the following conclusion,if a state satisfies

then it is separable,otherwise,it is entangled.

Any three-qubit fully separable state can be written as

We use Bloch representation expression to obtain

wherex0=y0=z0=1,x1=sinθAcosϕA,x2=sinθAsinϕA,x3=cosθA,y1=sinθBcosϕB,y2=sinθBsinϕB,y3=cosθB,and similar expressions forzkcan be represented withθCandϕC. Then

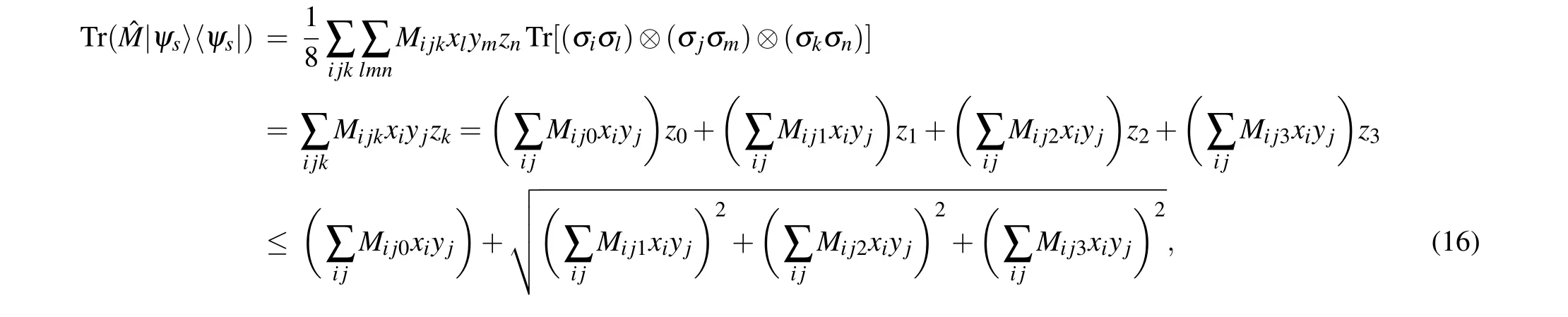
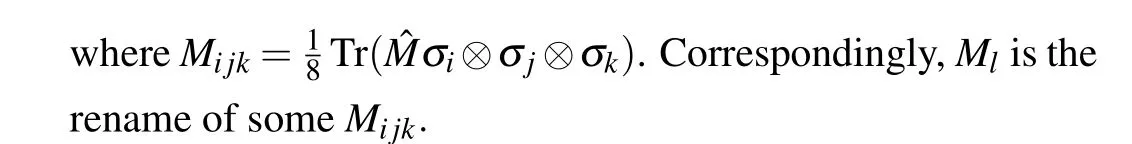
Finally,the maximum value ofΛcan be obtained according to the following expression:

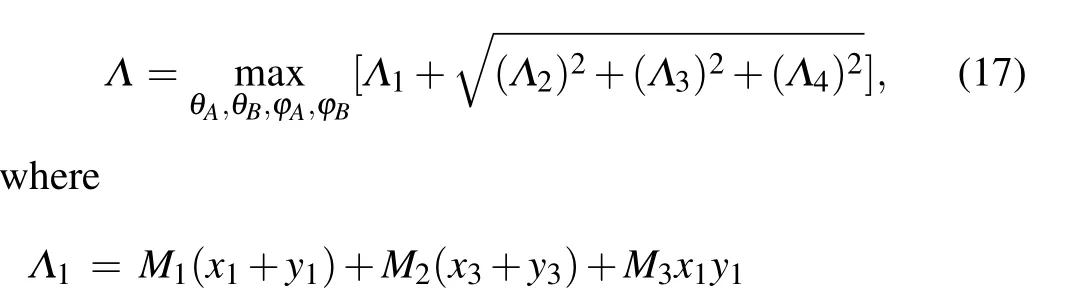
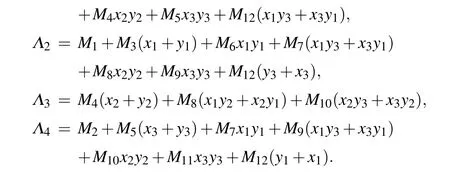
The maximum value ofΛis only related toθA,θB,ϕA,ϕB,and in the process of calculating the witness for the superposition state, we find thatθiandϕi(i=A,B) have a certain relationship.Λis achieved whenθA=θB, andϕA=ϕBorϕA=−ϕB. The maximum value ofΛcalculated by Eq.(17)is a function ofMi. After random searching ofMito find the minimum value ofℒ,we can obtain the matched entanglement witness.

4. Comparison of three methods

It can be clearly seen from Figs.1 and 2 that there is no unified generalized Wootters formula and PPT criterion that completely explain the full separability of the superposition state of the three-qubit GHZ state and the W state.

Fig.1. Necessary conditions ofseparability for ρ =w|W〉〈W|+g|GHZ〉〈GHZ|+(|W〉〈GHZ|+|GHZ〉〈W|)+ I8 at τ =0.25and τ =0.5.Thenumerical necessary condition is thenumerical calculation of matched entanglement witness.

The generalized Wootters formula we constructed can only be used to explain the part close to the W state,in this part the numerically calculated results of matched entanglement witness coincide with the generalized Wootters formula. As the decay factor decreases,the range of coincidence increases,the superposition state is with the least coincidence range.The approximate range that the two curves overlap in the superposition state isΘ ∈(0◦,14◦); whenτ=0.75, the range isΘ ∈(0◦,20◦);whenτ=0.5,the range isΘ ∈(0◦,29◦);whenτ=0.25,the range isΘ ∈(0◦,33◦),whereΘ=arctan(g/w).We also find that the PPT criterion is superior to the generalized Wootters formula except for the part near the W state.

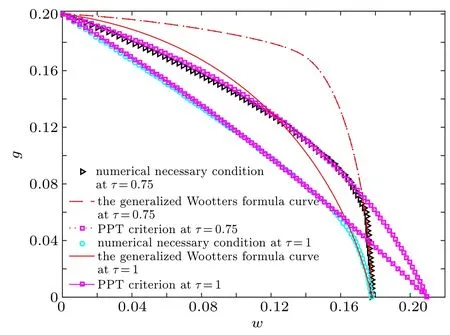
Fig. 2. Necessary conditions of separability for ρ = w|W〉〈W|+g|GHZ〉〈GHZ|+(|W〉〈GHZ|+|GHZ〉〈W|)+ I8 at τ =0.75 and τ =1. The numerical necessary condition is the numerical calculation of matched entanglement witness.

5. The relationship between entanglement and coherence

Quantum coherence depends on the choice of basis. In thed-dimensional Hilbert space,we choose an orthogonal basis{|i〉}di=1,if a quantum state can be expressed as a diagonal matrix in the basis then it is called an incoherent state(otherwise it is a coherent state),

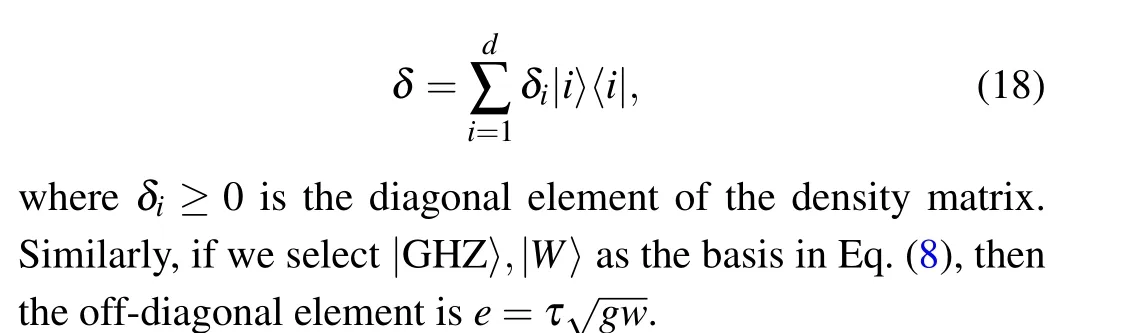
Thel1-norm of coherence[30]is an intuitive coherence measure based on the off-diagonal elements of the density matrix. It is defined as

whereIis the set of incoherent states. It exactly corresponds to the sum of the absolute values of all off-diagonal elements of the quantum state density operator. According to formula(19), the expression of coherence measure of the superposition state can be written as

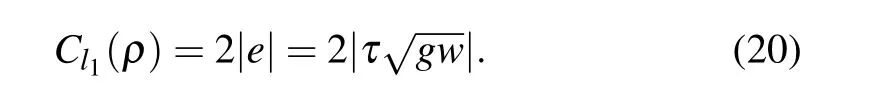
Note that the mixed state of the three-qubit GHZ state and W state(incoherent state)isσ,we denote the difference of white noise tolerance between the target stateρiandσasD,wherei=2,3,4,5 correspond to the states withτ=0.25,τ=0.5,τ=0.75,τ=1, respectively; theℒminfor stateσis denoted asr1,and theℒminfor the target stateρiis denoted asri,then the expression for D can be written as The graphs ofΘ–DandΘ-coherence are given in Figs.3 and 4.

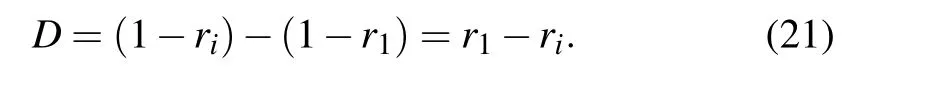
It can be seen from the figures that the relationship betweenDand coherence is that they are positively correlated.

Fig.3. The coherence and entanglement property of τ =0.5 and τ =0.25.

Fig.4. The coherence and entanglement property of τ =0.75 and τ =1.

6. Conclusion

We have conducted a separable condition study on the superposition state of the three-qubit GHZ state and the W state in a noisy environment and extended it to its decayed states(τ=0.25,0.5,0.75). After a series of calculations,we obtain the numerical results of separability by the matched entangled witness. Then we compare the numerical results of separability by the matched entanglement witness with the generalized Wootters formula and PPT criterion. The comparison results can be seen from Figs.1 and 2. We draw a conclusion that the generalized Wootters formula can be used as a tight criterion for the separability of the superposition state of the three-qubit GHZ state and the W state in the part close to the W state and its decayed states in white noise environment. The PPT criterion is superior to the generalized Wootters formula except for the part near the W state. In the study of coherence, we find that entanglement and coherence are positively correlated.