基于指数分布论域模糊PID的超精密金刚石车床导轨运动控制*

李兆中 岳晓斌 孙守利 阳 红

(中国工程物理研究院机械制造工艺研究所，四川 绵阳 621900)

超精密金刚石车床(single point diamond turing, SPDT)是超精密加工的重要设备之一，主要用于加工具有复杂表面形状或特殊表面形状要求的光学部件。许多国防尖端产品零部件，例如陀螺仪、高精度平面镜/透镜、精密仪器以及大功率激光系统中的多种零部件，需要用到超精密金刚石车床加工[1-4]。由于零件的表面形貌和刀具与工件之间的相对运动直接相关，因此零部件的高表面精度要求超精密金刚石车床导轨的伺服控制系统具有极高的定位精度、极高的响应速度和极小的稳态误差[5]。

超精密金刚石车床的伺服控制系统采用从里到外依次为电流环、速度环和位置环的三环控制方案。目前应用于超精密金刚石车床的主流控制算法是基于UMAC等运动控制器的PID控制算法。然而超精密加工存在非线性等时变因素，这使得传统的PID控制很难适应由运动位置变化、负载扰动及外界干扰等非线性因素引起的参数摄动及蠕变等，进而影响超精密切削加工精度及稳定性。针对这一问题，目前广泛采用的方法是将模糊控制引入到PID参数调节中[6]。模糊PID控制提高了系统的自适应性，然而模糊PID的控制效果依赖于初始PID参数的选取和论域的确定，使得应用较为复杂。为了解决上述问题，本文提出了一种论域范围优化方法，并引入到模糊PID控制中，实现自主学习并提高系统静动态性能，进而提高超精密切削加工精度。

本文对自研超精密金刚石车床导轨进行数学建模，通过MATLAB/ Simulink仿真对比了PID参数对控制对象阶跃响应的影响规律，总结出了论域范围优化方法，据此提出指数分布论域模糊PID控制算法，并和传统的定参数PID作比较。仿真结果表明，指数分布论域模糊PID控制具有更优的控制效果，提升了导轨响应速度。

1 超精密金刚石车床导轨理论模型及PID控制方法

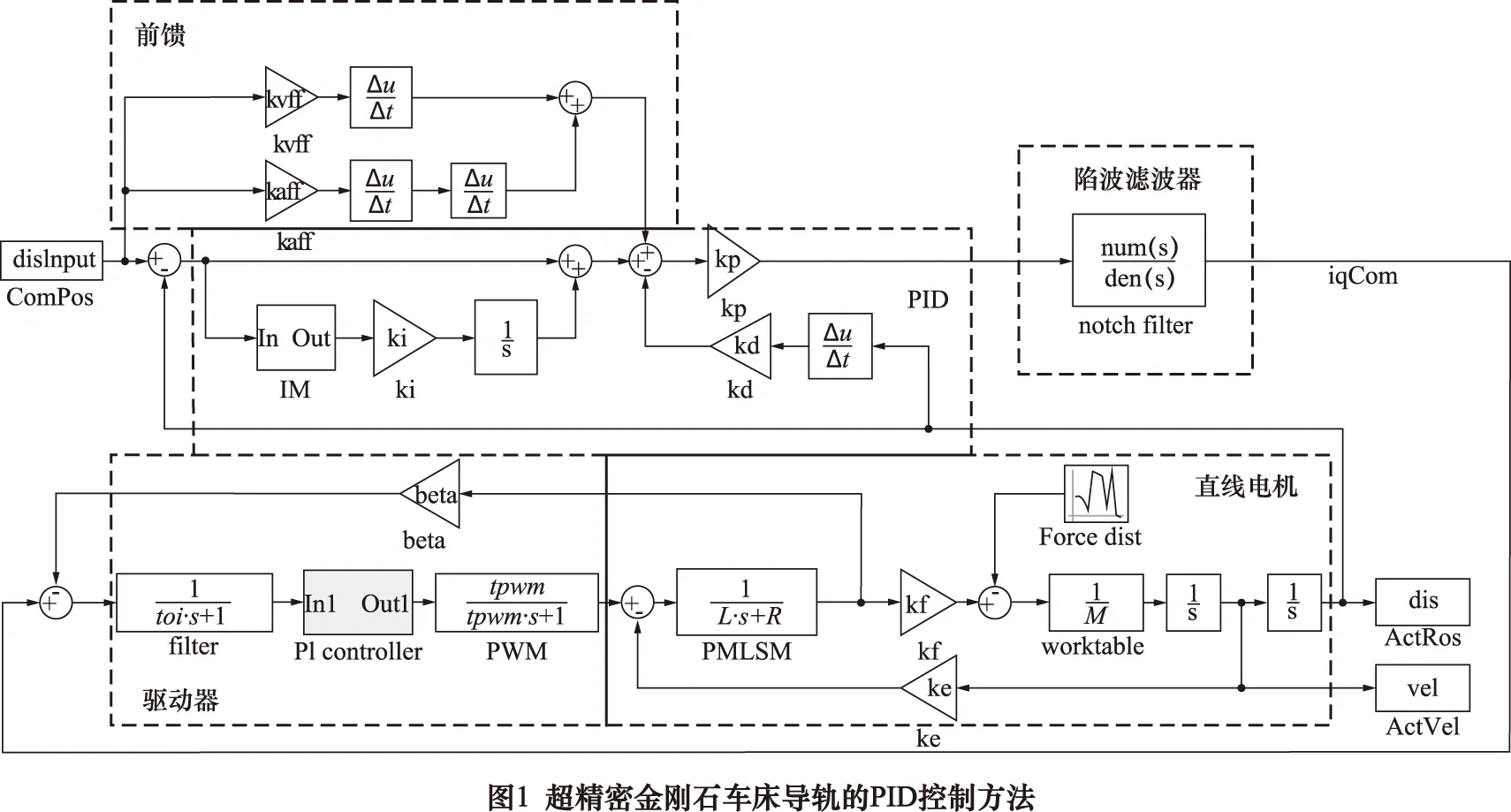
控制方案和控制对象的建模依赖于所选用的器件及其链接方式，本文的控制对象为自主研制的超精密金刚石车床导轨，该导轨为液体静压导轨，其具有高承载、高刚度和低摩擦等特性。驱动单元选用直线电机直接驱动。控制方案采用从里到外依次为电流环、速度环和位置环的三环控制，其中电流环闭环到直线电机配套驱动器中，采用PI控制，速度环和位置环闭环到UMAC运动控制器中，采用PID控制，主要包括PID、前馈、积分模式(integral mode, IM)和陷波滤波器(notch filter, NF)4个模块，如图1所示。

超精密加工存在的由运动位置变化、负载扰动及外界干扰等非线性因素，使得传统的PID控制无法满足高定位精度、高响应速度的要求，因而应用场景受限。

2 指数分布论域模糊PID控制方法

为解决传统PID难以适应超精密加工中存在多种非线性扰动的问题，引入模糊控制器，根据位置反馈信号的偏差E和偏差变化率EC对控制器参数Kp、Ki和Kd进行在线整定，使控制系统具有良好的动静态性能。在下文中未说明单位时，统一采用国际单位制(SI)。模糊控制器首先对误差信号及其变化率做模糊化处理，即论域上定义若干个模糊集合，并规定其隶属函数，进而将清晰的输入量转换为模糊量。本文中对模糊控制器的输入量E、EC都定义了7个模糊集合NB、NM、NS、ZO、PS、PM、PB。输入量的论域根据定参数PID控制方案下的闭环阶跃响应确定，其中E的论域定为[-1×10-5, 1×10-5]，EC的论域定为[-3×10-5, 3×10-5]。输入量的隶属函数都采用高斯型函数，如图2所示。

模糊控制器的核心是模糊控制规则表，即根据误差信号及其变化率的所属模糊集合确定控制器输出信号的所属模糊集合。本文采用mamdani模糊推理模型，使用的模糊控制表如表1～3所示。

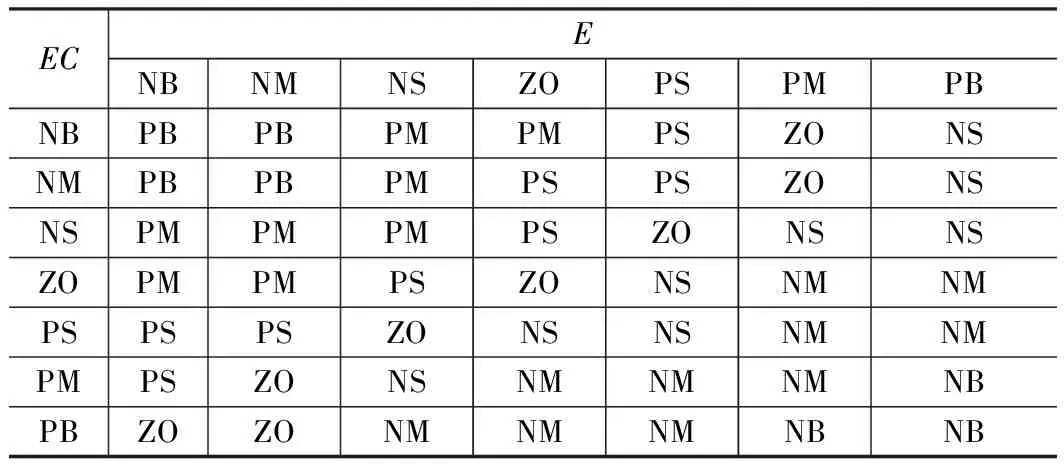
表 1 ΔKp的模糊控制规则表

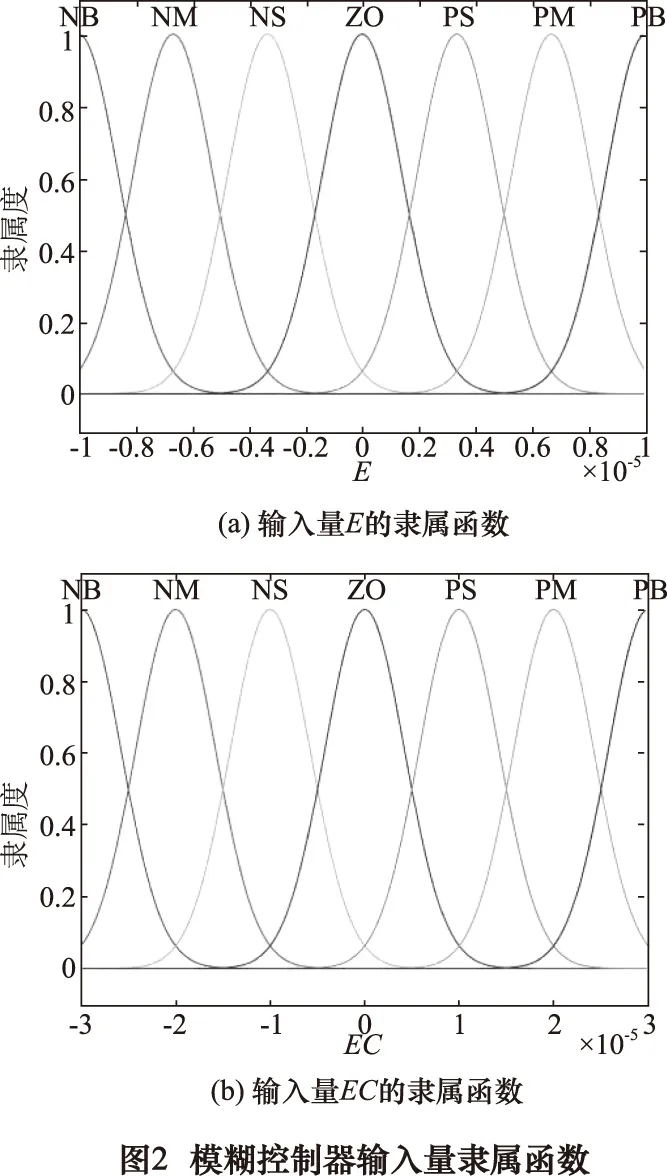
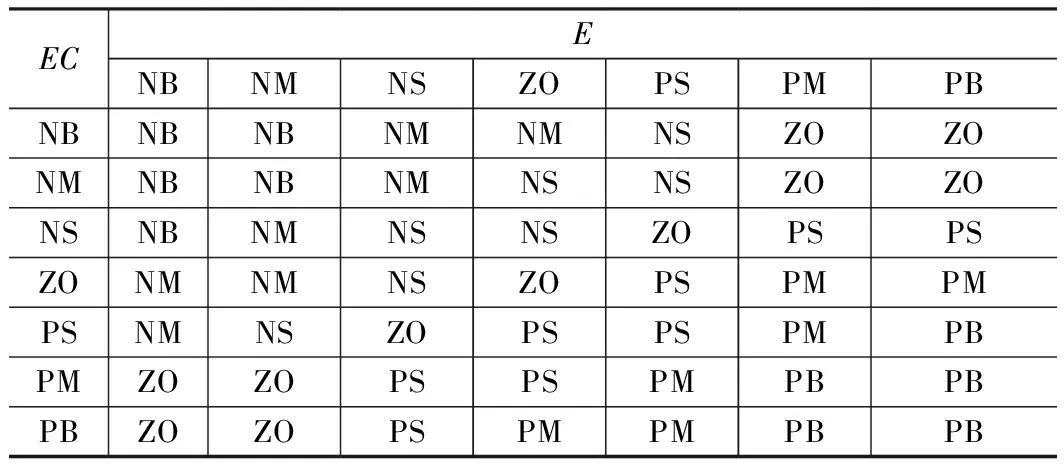
表2 ΔKi的模糊控制规则表

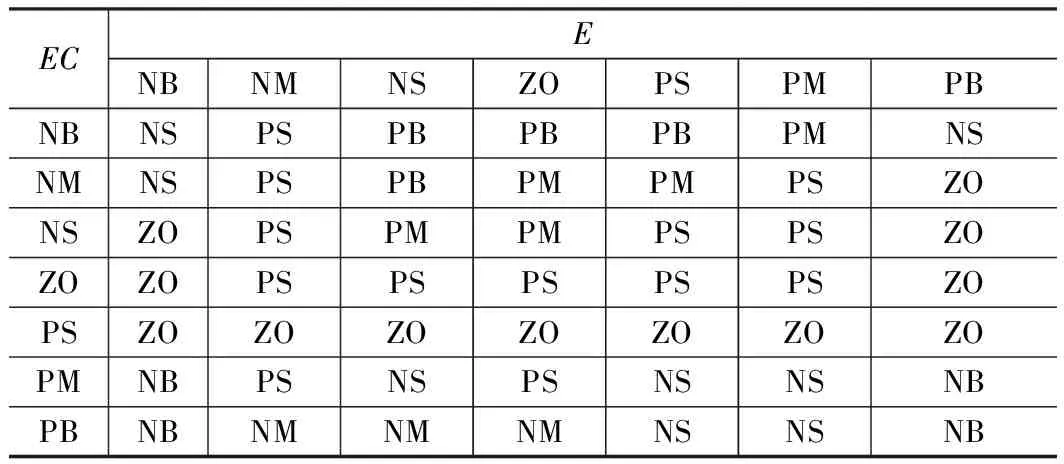
表3 ΔKd的模糊控制规则表

模糊控制器的输出是PID控制器参数的调整值ΔKp、ΔKi和ΔKd，根据模糊控制表求得的输出量仍是模糊量，通过解模糊的过程将其变成清晰量，本文中解模糊方法选用中心法(centroid)。最后通过Kp=Kp0+ΔKp、Ki=Ki0+ΔKi、Kd=Kd0+ΔKd在线整定PID参数，其中Kp0、Ki0和Kd0为PID控制器参数的初始值，Kp0= 500，Ki0= 0.1，Kd0= 0.3。

模糊控制器的控制品质较大程度上受PID参数初始值和论域范围选取的影响[7]。传统的模糊PID控制一般在确定总体的论域范围之后，再对单一模糊量下的不同隶属函数进行论域范围均等划分。针对固定论域的模糊PID控制，有学者提出了变论域模糊控制[8-10]，即根据被控信号的误差及其变化率，实时改变模糊控制器的论域范围。这种方法确实能取得更好的控制效果，然而其缺点在于论域变化规律复杂，且实时计算增大了计算负担。因此在不使控制器结构变复杂的前提下优化控制效果，需要具体地研究PID参数对控制效果的影响规律，再有针对性地优化模糊PID控制器的论域分布。

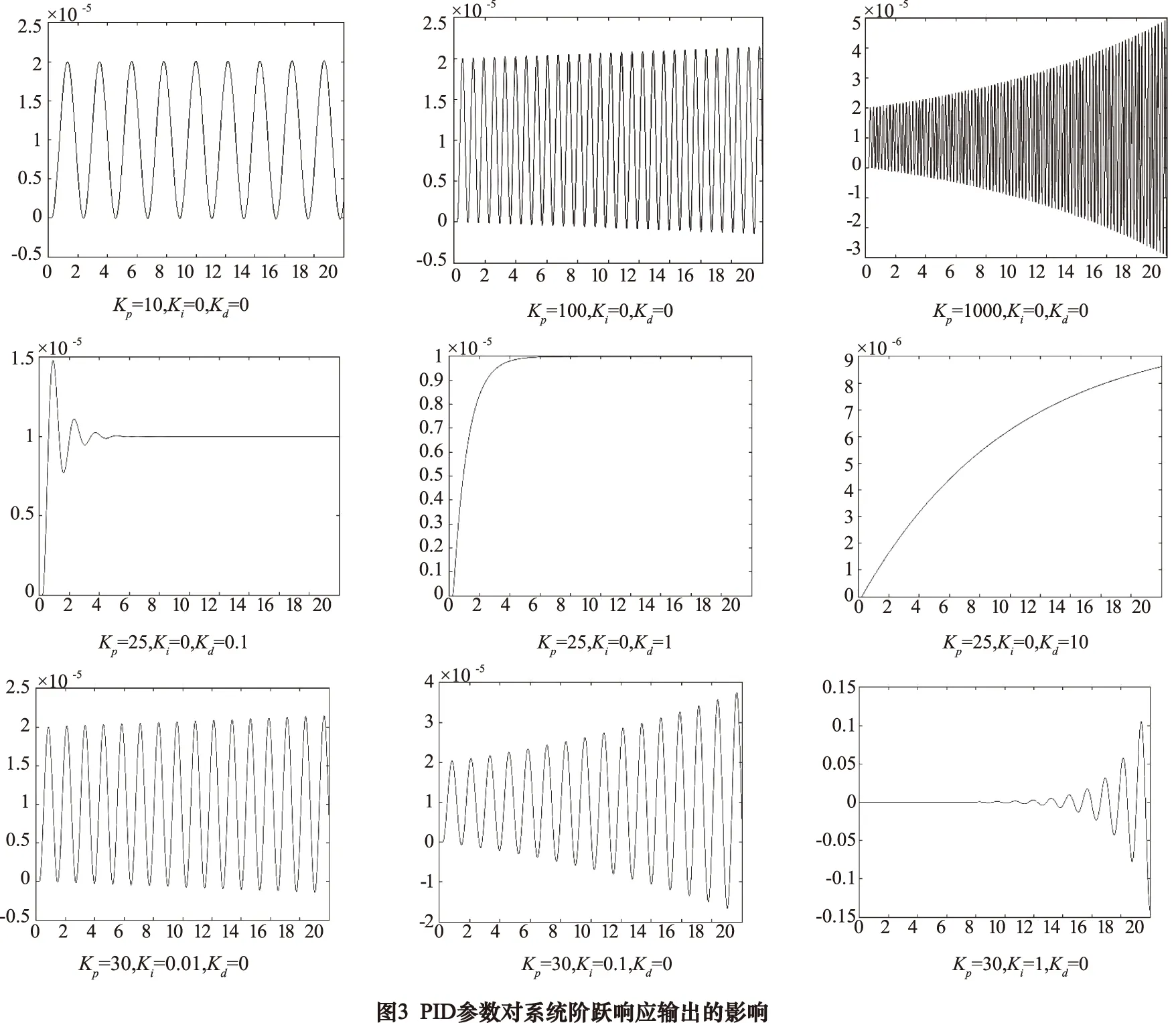
如图3所示，通过对PID参数调试，发现对于图1所示的控制系统，PID参数的影响呈现如下规律：在Kp> 0,Ki=Kd= 0时，系统阶跃响应输出是振荡的，增大Kp会使振荡频率变高并使系统输出趋向发散；在Kp> 0,Ki= 0,Kd> 0时，系统阶跃响应输出能稳定在指令值附近，且随着Kd变小，调整时间越短、超调量越大；在Kp> 0,Ki> 0,Kd= 0时，系统阶跃响应输出是振荡的，增大Ki不会改变振荡频率，但会使系统输出趋向发散。由此可以看出PID参数对系统阶跃响应输出的影响并不是线性的，要使系统阶跃响应快速且超调量小，应该增大Kp但不至于引起发散，并且在Ki、Kd大于0的情况下减小Ki、Kd。显然，均等分布论域的模糊PID无法满足上述需求，为此应使模糊控制器输出量ΔKp的论域正半部分增大，ΔKi、ΔKd论域的负半部分增大。

根据上述推论，构造模糊控制器输出量隶属函数，

其具有如下特征：

(1)每个输出量的隶属函数都采用三角隶属函数，形式如下：

式中：ξa、ξb、ξc是三角隶属函数的从左到右3个控制点的横坐标，用于控制三角隶属函数的形状，满足ξa<ξb<ξc。

(2)每个输出量具有7个模糊子集，模糊子集NB、NM、NS、ZO、PS、PM、PB的隶属函数用μi(ξ)表示，其中i=1,2,…,7，且具有ξb,k=ξa,k+1,k=1,…,6的关系，即对于两个相邻的隶属函数，右侧隶属函数的左控制点的横坐标与左侧隶属函数的中控制点的横坐标相同。

(3)每个输出量的隶属函数控制点横坐标具有如下关系

式中：α=(α1,α2,α3)T为论域分布参数，且有α1∈[0.01,1]、α2∈[1,2]、α3∈[1,2]，i=1,2,…,7分别对应NB到PB 这7个模糊子集。

该模糊控制器的输出量的隶属函数论域长度从左到右呈指数式变化，因而称之为指数分布论域模糊PID控制器，其中参数α=(α1,α2,α3)T为该控制器的特征参数，用于模糊控制器输出量隶属函数分布情况。图4所示为α=(0.4,1.25,1.8)T时的模糊控制器输出量隶属函数分布图。

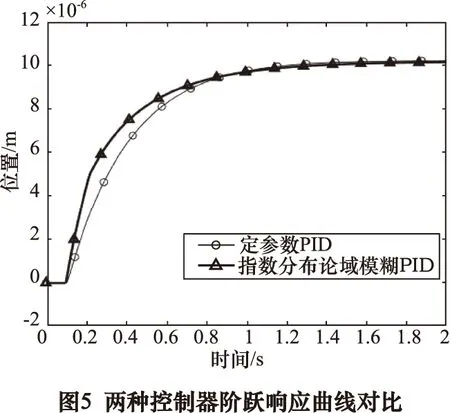
图5对比了定参数PID和指数分布论域模糊PID控制器下的系统闭环阶跃响应曲线，其中阶跃信号幅值为10 μm，于0.1 s时发生阶跃。指数分布论域模糊PID控制器的超调量为1.92%，比定参数PID减小了26.44%，调整时间为0.72 s，比定参数PID减小了11.42%，这证明了论域优化方法的有效性。

3 结语

本文通过Matlab/ Simulink仿真分析了PID参数对控制效果的影响规律，给出了一种模糊PID论域范围优化方法，并对比了传统定参数PID和指数分布论域模糊PID的控制效果。仿真结果表明，指数分布论域模糊PID控制的阶跃响应的调整时间更短，控制效果更优。