基于遗传算法的增/减材复合零件拉伸性能的多目标优化*

李亮亮 李鹏飞 刘 洋 张 腾

(①沈阳飞机工业(集团)有限公司工艺研究所，辽宁 沈阳 110000；②江苏大学机械工程学院，江苏 镇江 212013；③常熟市科技局，江苏 苏州 215500)

英国著名杂志《经济学家》发表了一篇专题报道，称全球产业正在经历第三次工业革命[1-2]，其中极具代表性的技术之一是3D打印技术[3]。3D打印尽管是一种非常高效的制造方法，但在产品的尺寸精度和表面粗糙度上，加工效果并不理想[4]。而传统减材制造具有的加工精度高，易于切削加工材料等特点。可以看出，增材制造与减材制造的优缺点具有很强的互补性。因此，将增材和减材加工工艺复合起来实现“净成形”目标，具有广阔的应用前景[5-6]。

目前对于增减材复合制造技术，英国巴斯大学学者Zhu Z、Flynn J M等就激光增材/机加减材复合制造工艺的新理念，分析了增减材复合制造工业前景，并指出增减材复合制造技术能够突破增材制造零件尺寸和形状精度低的瓶颈，也可以解决复杂结构受传统减材工艺的限制问题[7-8]。德国德玛吉公司和美国加利福尼亚大学合作的Hansel A和Mori M等研究了增减材复合制造工艺的合理工艺条件，并对 SUS 316 和 Inconel 625 材料增材成形件进行拉伸性能实验，结果指出 SUS 316 增材成形件工艺参数合理，屈服强度达到锻件水平[9]。

然而，该技术仍处于起步阶段。为了充分发挥该技术的优越性，对成形试样的基本问题研究仍是目前研究的重点之一，如增/减材复合加工工艺匹配控制策略对成形件的形控、性控等方面的影响。因此，本文基于遗传算法就激光熔覆工艺参数对增/减材复合零件的拉伸性能的影响展开了研究。

1 试验步骤

1.1 试验材料

本实验所用的粉末材料为 316 L不锈钢粉末，尺寸为100～270目(0.053～0.15 mm)，其成分如表1所示。在试验进行前，对粉末进行烘干，减少吸潮对成形零件质量可能带来的影响。

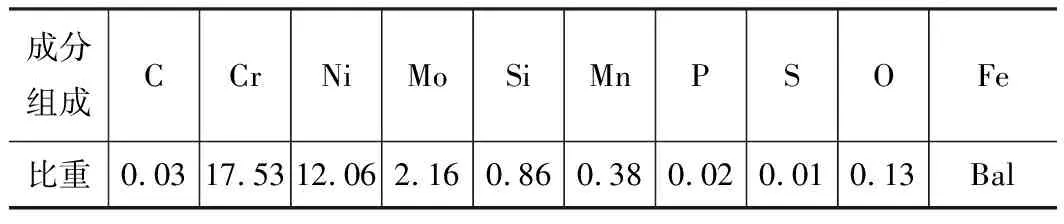
表1 316L不锈钢粉末化学成分 %

1.2 试验设备

本试验采用的试验设备是大连三垒SVW80C-3D增减材复合五轴加工中心。该加工中心是金属喷粉激光熔融与立式加工中心复合机床。图1a为增材加工装置，采用光纤二极管激光器，激光器功率2 kW；图1b为减材铣刀装置。

1.3 试验方法

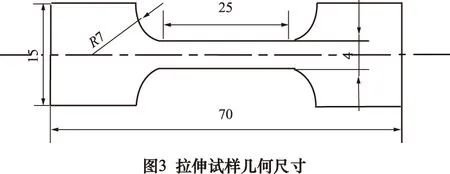
本实验采用增/减材复合加工方法，利用激光熔覆工艺加工单道多层薄壁试样，在冷却2 min后，采用铣刀立刻进行铣削，保证薄壁试样的厚度为2 mm，铣削当前温度250±50 ℃。默认Z轴抬升量选为0.6 mm，切削当前温度为200 ℃，主轴转速为2 000 r/min，进给速度为1 500 mm/min。采用正交试验(表2所示)来制备试样，扫描方式为往返双向扫描。拉伸试样切割位置如图2所示，按照图3对试样进行线切割，所制备的试样外观如图4所示。在室温20 ℃的条件下，使用电子万能测验机，加载速率2 mm/min，进行静载位移控制拉伸实验。

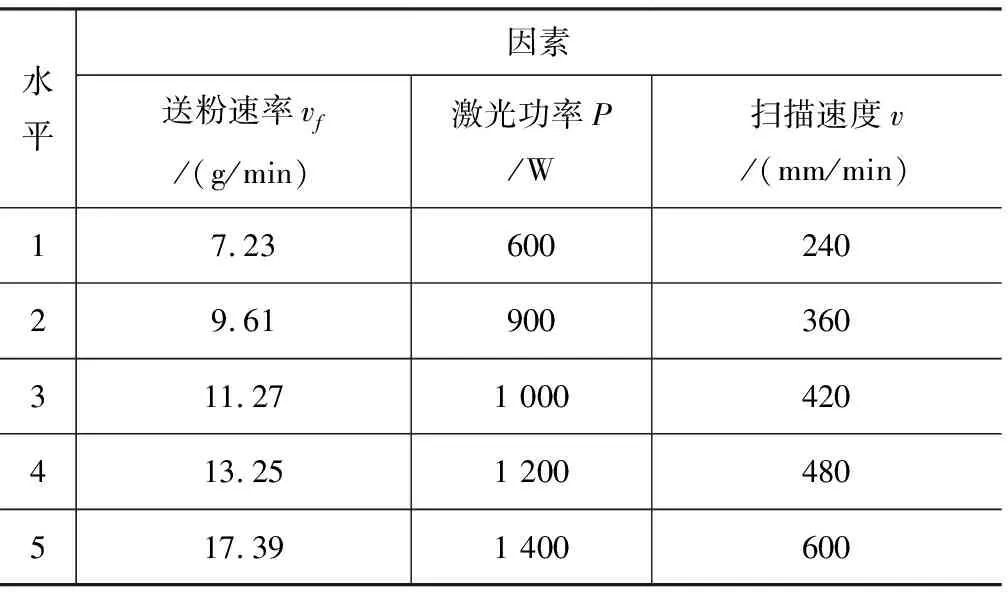
表2 正交试验参数

2 试验结果与分析

2.1 正交试验结果

得到拉伸试验结果如表3所示。查GB/T 4237-2007可知316 L不锈钢的拉伸强度为 485 MPa，成形薄壁件的性能基本达到标准，激光熔覆成形的薄壁件试样的抗拉强度优于不锈钢热轧钢板的标准抗拉强度。

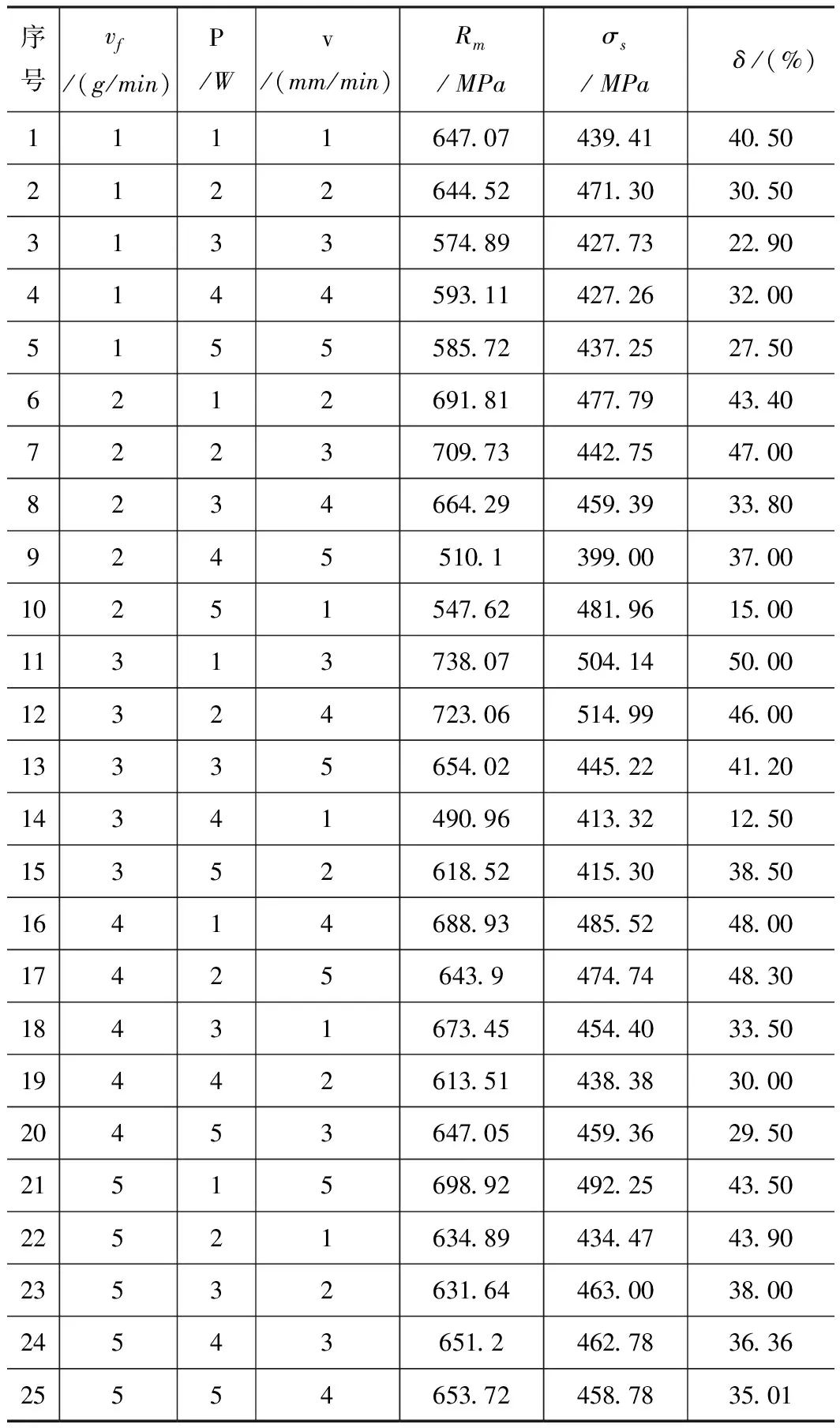
表3 拉伸试验结果

2.2 数学模型的建立

采用多元线性回归的方法对抗拉强度、屈服强度和伸长率关于送粉速率、激光功率、扫描速度的经验公式进行拟合，假设多元线性回归模型为式(1)：

y=α0+α1x1+α2x2+…+αm-1xm-1

(1)

模型中各系数与常数项利用最小二乘法求得。得到如下拟合模型：

(1)抗拉强度Rm模型方程，见式(2)：

0.000 160 35×P2-0.000 799 837×v2+

0.013 666 612×vf×P- 0.020 893 351 2×vf×v-

0.000 142 511 2×P×v+ 19.807 818 17×vf-

0.558 799 625×P+ 1.250 192 873×v

(2)

模型的F=13.932 6，P=0.000 3，表明模型有统计学意义，说明包含3个自变量的回归方程可解释抗拉强度变异性的93.30%。

(2)屈服强度σs模型方程，见式(3)：

0.000 403 945×P2-0.000 507 364×v2+

0.003 509 512×vf×P-0.024 740 097×vf×v-

0.000 526 411×P×v-6.995 480 932×vf-

0.663 871 22×P+1.238 416 002×v

(3)

模型的F=16.15，P=0.001 5，表明模型有统计学意义，说明包含3个自变量的回归方程可解释抗拉强度变异性的96.04%。

(3)伸长率δ模型方程，见式(4)：

2.92×10-7×P2+ 1.07×10-6×v2+

4.04×10-5×vf×P- 0.000 114 35×vf×v-

4.18×10-7×P×v+ 0.044 743 232×vf-

0.001 159 582×P+0.001 231 823×v

(4)

模型的F=91.12，P=0.000 0，表明模型有统计学意义，说明包含3个自变量的回归方程可解释抗拉强度变异性的98.91%。

2.3 基于遗传算法的单目标优化

2.3.1 以抗拉强度为评价指标

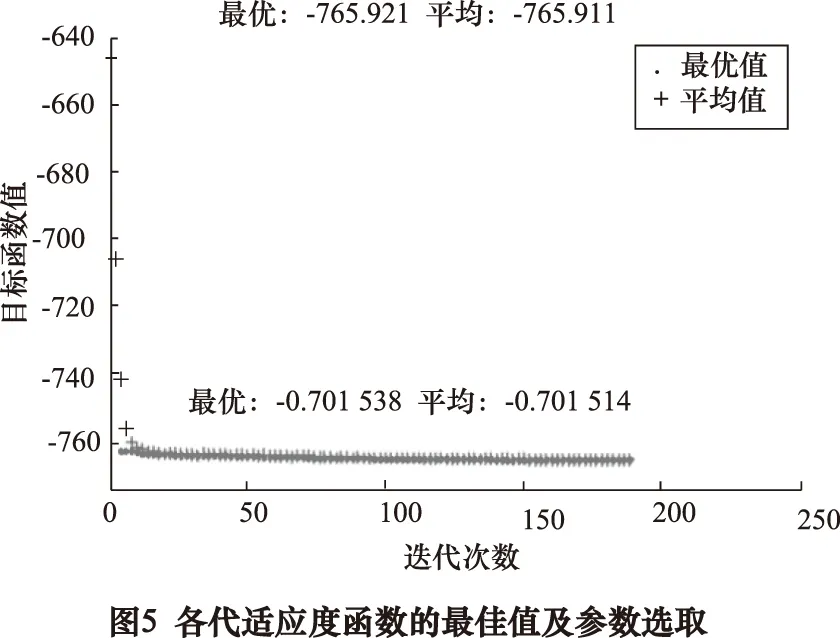
当算法种群规模N=100，交叉概率pc=0.8，变异概率pm为0.2，选择概率为0.5，最大遗传代数为250，运行算法，结果如图5所示。图中底部的点表示各代最佳适应度值，其上的点表示各代平均适应度值。算法在184次迭代时结果趋于平衡。其最佳的工艺参数为送粉速率8.71 g/min，激光功率600 W扫描速度600 mm/min，这时，抗拉强度为 765.92 MP。

2.3.2 以屈服强度为评价指标

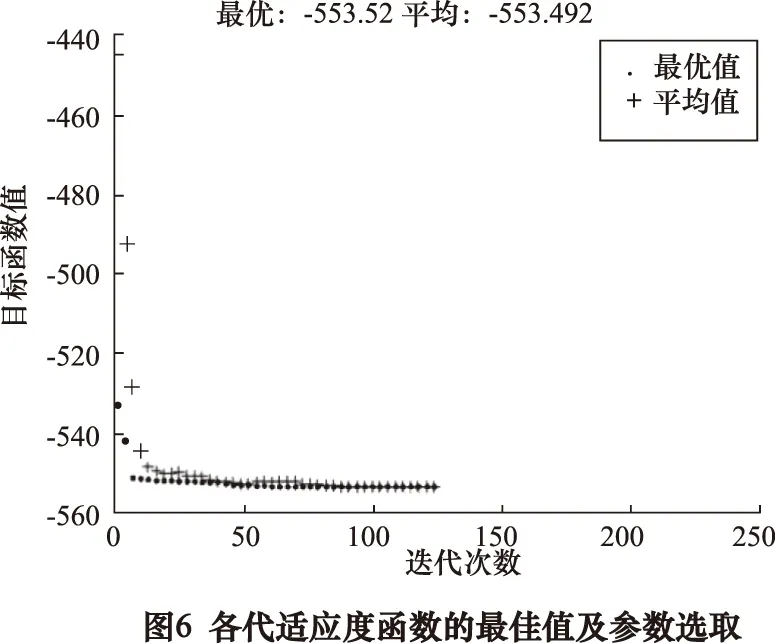
当算法种群规模N=100，交叉概率=0.8，变异概率为0.2，选择概率为0.5，最大遗传代数为250，运行算法，结果如图6所示。图中底部的点表示各代最佳适应度值，其上的点表示各代平均适应度值。算法在138次迭代时结果趋于平衡。其最佳的工艺参数为送粉速率7.23 g/min，激光功率600 W扫描速度600 mm/min，此时，屈服强度为 553.52 MPa。

2.3.3 以伸长率为评价指标

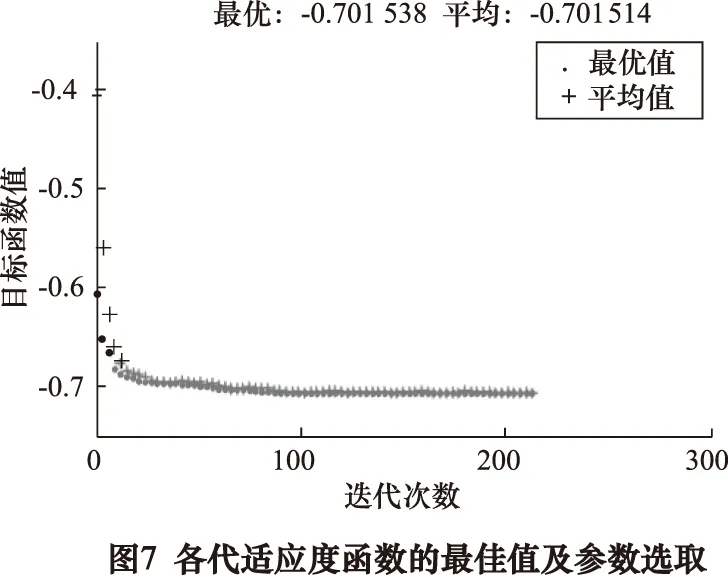
当算法种群规模N=100，交叉概率pc=0.8，变异概率pm为0.2，选择概率为0.5，最大遗传代数为300，运行算法，结果如图7所示。图中底部的点表示各代最佳适应度值，其上的点表示各代平均适应度值。算法在211次迭代时结果趋于平衡。其最佳的送粉速率7.229 g/min，激光功率600 W，扫描速度600 mm/min，伸长率为 70.15 %。

2.4 基于遗传算法的拉伸性能多目标优化

2.4.1 多目标遗传算法的基本思想

需要同时优化多个目标函数的问题通常被称为多目标优化问题。目前对于多目标优化大多采用传统的权重法，即将多个目标函数加权整合为单个目标函数来进行优化。加权求和方法易于理，可以很容易地建立起数学模型，而且计算速度快，以其便捷性得到了广泛的应用。本文采用加权求和法来解决拉伸性能多目标优化问题。

2.4.2 数据的预处理

在遗传算法计算中，不同目标函数数据的绝对值范围不一致，数值相差过大，如果不对数据进行处理，会对预测结果产生十分不利的影响。因此，在进行MATLAB遗传算法多目标优化前，需要对目标函数值进行归一化预处理。本文采用归一化公式如式(5)：

(5)

2.4.3 多目标优化的线性加权

线性加权法就是将多目标的加权和作为单目标，即将多目标优化问题，如式(6)。

minF(X)=[f1(X),f2(X),…,fm(X)]T

s.t.gu(X)≥0u=1,2,…,p

hv(X)≥0v=1,2,…,q

(6)

转化为式(7)转化为：

(7)

s.t.gu(X)≥0u=1,2,…,p

hv(X)≥0v=1,2,…,q

本文采用加权系数分别为ω1=0.25,ω2=0.25,ω3=0.5；得到目标函数为min-u=-0.25Rm-0.25σs-0.5δ。

2.4.4 多目标优化结果

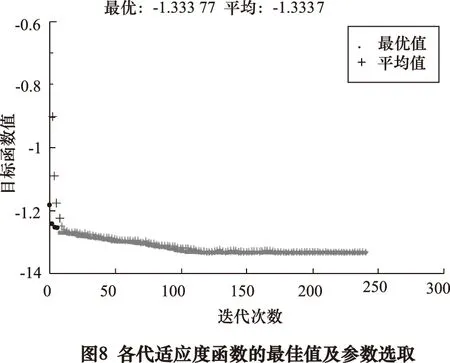
利用MATLAB遗传算法工具箱对目标函数进行优化。当算法种群规模N=100，交叉概率pc=0.8，变异概率pm为0.2，选择概率为0.5，最大遗传代数为300，运行算法，结果如图8所示。图中底部的点表示各代最佳适应度值，其上的点表示各代平均适应度值。算法在245次迭代时结果趋于平衡。前20次的迭代运算中数据变化较大，第20次迭代后数据变化几乎可以忽略，其最佳的送粉速率7.239 g/min，激光功率600 W，扫描速度600 mm/min，抗拉强度为763.981 4 MPa，屈服强度为553.520 4 MPa，伸长率为 0.701 540。

2.4.5 优选工艺参数验证

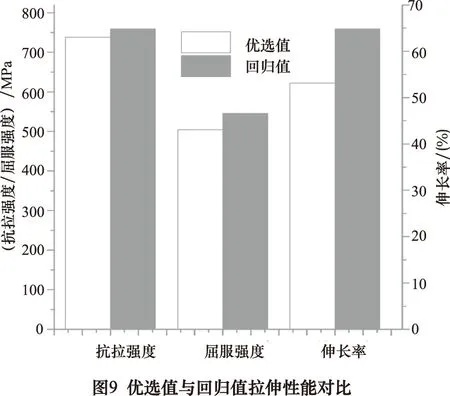
为了验证优化工艺的合理性，在正交试验基础上进行了验证试验，结果如表4、图9能明显看出回归模型的抗拉强度、屈服强度和伸长率明显强于优选的结果，抗拉强度提高3.5%，屈服强度提高9.8%，伸长率提高40%。最终得出了抗拉强度、屈服强度和伸长率折中最优的工艺参数组合。

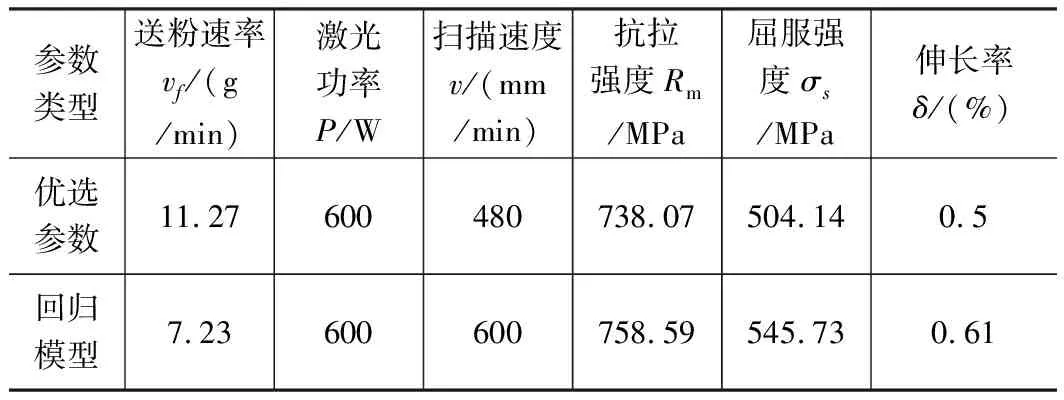
表4 优选工艺参数验证

3 结语

本次实验探究工艺参数对增减材复合加工的316L拉伸性能的影响，分别采用单目标和多目标遗传算法对工艺参数进行优化，可得出以下结论：

(1)根据正交实验数据，利用MATLAB拟合出工艺参数对抗拉强度、屈服强度和伸长率影响的回归方程。并通过比较F值、P值以及R2可知拟合模型合理，故可用于预测相同工艺条件的拉伸性能。

(2)本次试验利用遗传算法进行单目标优化可知：基于正交试验的前提下，送粉速率8.71 g/min，激光功率600 W，扫描速度600 mm/min，抗拉强度达到最优值为 765.921 0 MPa；送粉速率7.23 g/min，激光功率600 W，扫描速度600 mm/min，屈服强度达到最优值为 553.520 4 MPa；送粉速率7.23 g/min，激光功率600 W，扫描速度600 mm/min，伸长率达到最优值为 0.701 540。

(3)本次试验利用遗传算法进行多目标优化可知：送粉速率7.23 g/min，激光功率600 W，扫描速度600 mm/min得到拉伸性能最优值为抗拉强度763.981 4 MPa，屈服强度553.520 4 MPa，伸长率 0.701 540。为实际生产提供了参考依据。