动静摩擦因数对推焦系统动力学特性的影响∗

陈俊君，李 骏，孙桓五，段海栋

（1.山西大学自动化与软件学院 太原，030013）（2.太原理工大学机械与运载工程学院 太原，030024）（3.东北大学机械工程与自动化学院 沈阳，110819）

引言

大多数机械系统中都存在着摩擦引起的振动和噪声现象［1］，包括汽车制动系统、齿轮啮合系统、丝杠传动系统等常用的机械装置［2‐4］。机械装置摩擦接触面间产生的振动会导致接触界面的磨损和破坏，在某些情况下甚至会导致机械系统的失效。焦炉推焦装置的功能是将焦炉中成熟的红焦从炭化室中推出，推焦杆通过滑履与炭化室地面接触，在推焦作业过程中滑履与地面之间会产生强烈的摩擦，导致推焦装置产生复杂的振动。该振动一方面会引起噪声污染，另一方面也会加剧部件的疲劳和磨损，致使推焦系统的稳定性变差并且出现黏滑运动现象。稳定性变差指在工作过程中推焦装置的重心位置发生较大的改变，工程中表现为装置的垂直方向跳动和左右摇摆现象。黏滑运动指推焦装置在行进过程中出现的速度忽快忽慢的现象，表现为推焦装置的低频颤振。建立动力学模型［5‐6］是研究摩擦自激振动系统不稳定性及黏滑运动的一个重要手段，而且有助于设计控制器来消除系统的不稳定性和黏滑运动。目前，已经建立了一些摩擦自激振动模型用来解释不同的摩擦现象，如预滑动位移模型、Stribeck摩擦效应模型、黏滑运动模型和滞回效应模型［7］。预滑动位移模型主要描述静态阶段发生的微观运动。在系统处于稳定的低速状态下，摩擦力随相对速度的增加先减小后增大，摩擦力的这种下垂特性称为“Stribeck 摩擦效应”。一般情况下，在系统处于稳定状态下滑动摩擦力的数值是单值的；而在滑动速度振荡的非稳定状态下则是多值的，并且摩擦力响应曲线在减速和加速阶段具有不同的路径。在滑动状态下，迟滞环也称为摩擦记忆迟滞环，根据相对加速阶段摩擦力是否大于相对减速阶段的摩擦力，可以分为顺时针方向［8］和逆时针方向［9］两种形式。到目前为止，还没有通用的理论模型能够完全解释摩擦引起的振动现象。推焦作业过程属于一种典型的滑动摩擦，对于焦炉推焦系统还存在着动力学模型缺乏、振动理论的研究不够深入等问题［10］。因此，研究推焦系统的振动机理具有很强的理论和工程应用价值。

1 焦炉推焦自激振动系统建模

推焦装置是将炭化室内的红焦推出炭化室的具体执行机构，其主要结构包括推焦杆、齿轮齿条传动机构、滑履、支棍和推焦头。推焦装置的具体结构如图1 所示。其中，推焦杆是推焦装置的核心构件，笔者研究的6.25 m 捣固焦炉设备中推焦杆的重量约为40 t，长为27 m，宽为0.34 m，高为1.05 m。根据推焦系统的实际工作情况，笔者建立了一个两自由度的摩擦自激振动力学模型，如图2 所示。传送带以恒定速度v0向单一方向移动，传送带上有一滑块m，该滑块受到恒定的法向力N作用，在竖直方向通过两个线性弹簧k1和k2连接到竖直位置的固定端，在水平方向通过阻尼c和弹簧k3将其连接到水平位置的固定端，滑块和带之间的摩擦力F为滑块提供驱动力。

图1 推焦装置结构示意图Fig.1 The schematic diagram of the coke pushing device

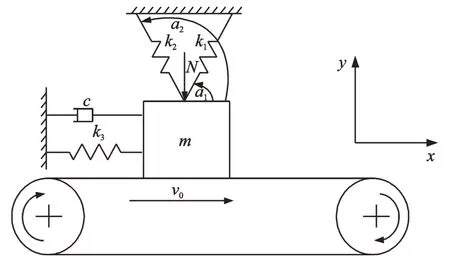
图2 推焦系统的力学模型Fig.2 Mechanical model of the coke pushing system

该模型的运动微分方程可由式（1）给出

其中：F为作用在滑块上的摩擦力。

使用式（2）的Stribeck 摩擦模型［11］进行计算，F定义为

其中：vr=表示滑块与传送带之间的相对滑动速度；μs为静摩擦因数；μm为动摩擦因数，μs≥μmN表示摩擦表面之间的正压力；vm为最小动摩擦因数对应的滑动速度，并且满足|μ(0)| ≤μs，|μ(vm)|=μm，μ′(vm)=0，μ(-vr)=-μ(vr)，μ′(-vr)=μ′(vr)，

滑块在移动带上静止时的相对速度vr的数值为0，当滑块在带上开始滑动时，摩擦力数值最初减小，而后随着速度的增加而增加。

2 系统的稳定性和黏滑运动特性理论分析

设ω0=可以获得式（3）所示的无量纲变量和参数

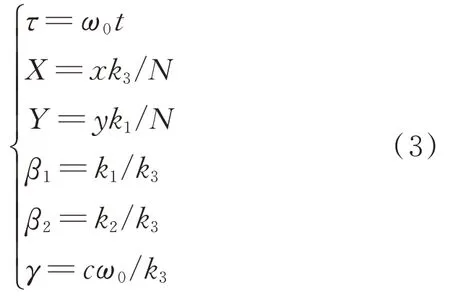
将式（3）代入式（1），求得系统运动微分方程的无量纲表达式为

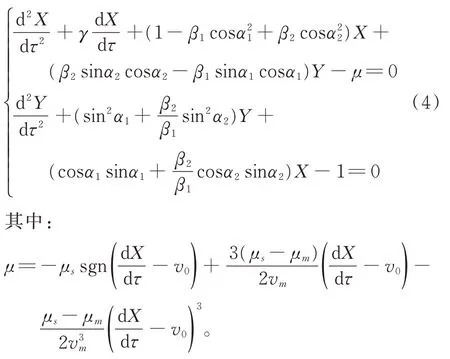
根据常微分方程理论，任何正规高阶微分方程都可以转化为等价的1 阶微分方程组。故对系统的微分方程进行等价变换，可以令

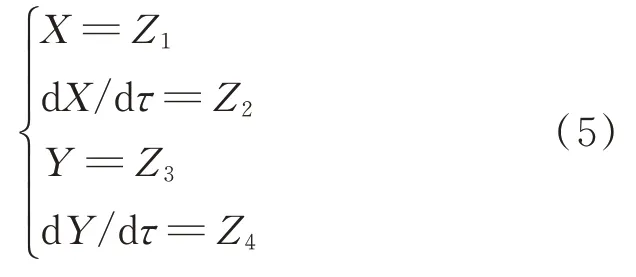
把式（5）代入式（4），可以得到如式（6）所示的1阶微分方程组

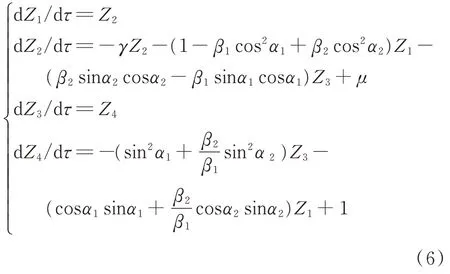
当系统输入速度足够大时，在摩擦力和弹簧力的作用下，滑块处于静平衡状态。在这种平衡状态下，系统初始条件设为：并且符号函数sgn(vr)=-1。系统参数值设置如下：μs=0.8，μm=0.6，vm=0.45 m/s。利用李雅普诺夫稳定性理论分析了系统平衡点的稳定性。当时，由式（6）可求得系统的平衡点为

将式（6）右端展开成泰勒级数，并略去二次以上的项，可以得到系统的1 阶近似微分方程的雅可比矩阵为

系统的无量纲参数设置如下：β1=β2=0.001，γ=0.02，α1=将上述参数代入式（8）可得矩阵A的特征方程为

使用文献［12］中的计算公式可以获得系统的临界黏滑速度为

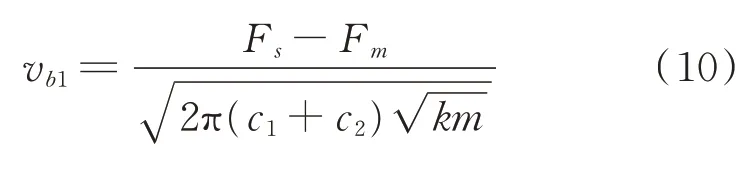
其中：Fs-Fm为静摩擦力和动摩擦力的差值；c1+c2为系统的阻尼；k为系统的等效刚度；m为滑块的质量。

本研究中各参数为：Fs-Fm=0.2，c1+c2=0.02，k=1，m=1。将以上各参数数值带入式（10）可求得系统的临界黏滑速度为0.564 3m/s。理论分析表明，当系统驱动速度低于该临界值时，滑块在运行过程中会出现黏滑运动现象；当系统驱动速度高于该临界值时，滑块在运行过程中不会出现黏滑运动现象。

为了对理论计算结果进行验证，笔者采用数值计算的方法求解了式（4）给出的焦炉推焦系统的运动方程，分析了不同驱动速度下系统的稳定性和黏滑运动特性。推焦系统仿真参数设置如下：β1=β2=0.001，γ=0.02，α1=π/3，α2=2π/3，M=1，Kx=1，Ky=1.5。在推焦系统中推焦装置材料为Q235 钢，炭化室地面为耐火砖，实际工作中炭化室内温度在1 000℃左右。推焦装置和耐火砖之间通过红焦接触，其表面情况非常复杂，根据企业工程实际经验，动静摩擦因数分别设定为［13］μs=0.8，μm=0.6。系统初始条件满足X=0，。系统驱动速度分别设置为：0.35，0.42，0.5，0.54，0.6，0.65 m/s。对系统进行仿真，获得的相图如图3所示。

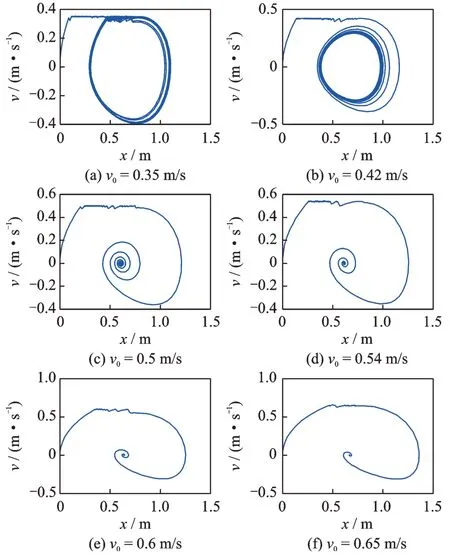
图3 不同驱动速度下的系统相图Fig.3 The phase diagrams with different excitation speeds

由图3 可知，驱动速度不同时，系统响应的数值计算结果也不同。从图3（a，b）中可以看出，当系统驱动速度低于系统临界失稳速度v0=vb0=0.444 4 m/s 时，系统处于不稳定状态，而且存在明显的黏滑运动现象；从图3（c，d）中可以发现，当系统驱动速度高于系统临界失稳速度而低于系统的临界黏滑速度0.564 3m/s 时，系统稳定在平衡点，黏滑运动依然很明显；图3（e，f）的相图表明，当系统驱动速度高于系统临界失稳速度和临界黏滑速度时，系统稳定在平衡点，同时不会出现黏滑运动现象。

通过推焦作业现场实际测试，发现推焦过程中推焦装置的平均工作速度一般为0.25～0.45m/s，该值低于系统的临界失稳速度和临界黏滑速度，表明推焦作业过程中容易发生黏滑振动现象。根据企业工程技术人员的现场经验，认为动静摩擦因数的差值可能对推焦装置的稳定性和黏滑振动有重要的影响，因此笔者采用数值仿真的方法详细分析了动静摩擦因数差值的变化对推焦装置稳定性和黏滑特性的影响。

为了更全面地分析问题，笔者将摩擦因数的变化分成了两种情况进行讨论：①在不改变静摩擦因数的前提下，通过增大动摩擦因数的方法来减小动静摩擦因数的差值；②在不改变动摩擦因数的前提下，通过减小静摩擦因数的方法来减小动静摩擦因数的差值。

3 动静摩擦因数变化对焦炉推焦系统稳定性的影响

3.1 静摩擦因数不变而动摩擦因数增大

仿真系统参数设置为：β1=β2=0.001，γ=0.02，α1=π/3，α2=2π/3，v0=0.4 m/s，M=1，Kx=1，Ky=1.5，μs=0.8。系统满足如下初始条件：X=0，=0，Y=0，=0。系统的静摩擦因数减去动摩擦因数的差值分别取为：0.2，0.1，0.05，0.02，0.01，0.001。对系统进行仿真，获得的相图如图4 所示，获得的Poincare 截面图如图5 所示。从图4 中可以看出，随着动静摩擦因数差值的不断减小，极限环外部的相轨迹逐渐卷向极限环，而且极限环不断地缩小，表明系统由不稳定状态逐渐转为稳定状态。由图5 中的Poincare 截面图可知，在不同动静摩擦因数差值的情况下，系统都能够进行准周期运动。

图4 静摩擦因数不变而动摩擦因数增大工况下的相图Fig.4 The phase diagrams with the condition of constant static friction factor and increasing dynamic friction factor

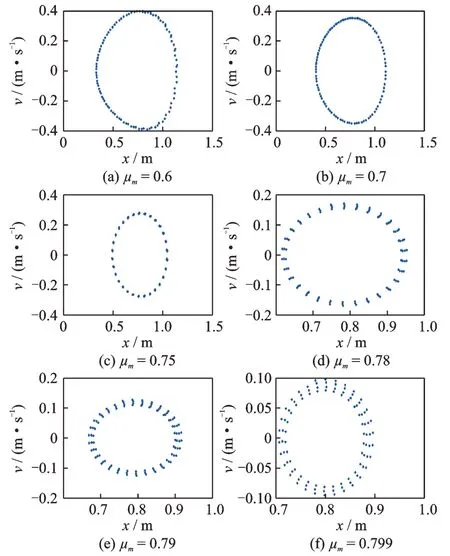
图5 静摩擦因数不变而动摩擦因数增大工况下的的Poin‐care 截面图Fig.5 The Poincare sectional views with the condition of constant static friction factor and increasing dynamic friction factor

3.2 动摩擦因数不变而静摩擦因数减小

仿真系统参数设置为：β1=β2=0.001，γ=0.02，α1=π/3，α2=2π/3，v0=0.4 m/s，M=1，Kx=1，Ky=1.5，μm=0.6。系统满足如下初始条件：X=0，=0，Y=0，=0。系统的静摩擦因数减去动摩擦因数的差值分别取为：0.2，0.1，0.05，0.02，0.01，0.001。对系统进行仿真，获得的相图如图6 所示，获得的Poincare 截面图如图7 所示。由图6 可以看出，随着动静摩擦因数差值的逐渐减小，极限环外部的相轨迹逐渐卷向极限环，而且极限环不断地缩小，表明系统由不稳定状态逐渐转为稳定状态。由图7 中的Poincare 截面图可知，在不同的动静摩擦因数差值情况下，系统都能够进行准周期运动。

图6 动摩擦因数不变而静摩擦因数减小工况下的相图Fig.6 The phase diagrams with the condition of constant dy‐namic friction factor and decreasing static friction factor

图7 动摩擦因数不变而静摩擦因数减小工况下的Poincare截面图Fig.7 The Poincare sectional views with the condition of constant dynamic friction factor and decreasing static friction factor

4 动静摩擦因数变化对焦炉推焦系统黏滑运动特性的影响

由图4 和图6 的相图分析结果可知，在改变动静摩擦因数差值的情况下，系统的黏滑运动现象一直存在。为了定量表征动静摩擦因数变化对焦炉推焦系统黏滑运动特性的影响，本节采用多体动力学仿真的方法对其进行了研究。

4.1 静摩擦因数不变而动摩擦因数增大

推焦系统仿真参数设置为：m=4.12×104kg，v0=0.5 m/s，k1=7.433×103N/m，k2=7.433×103N/m，k3=7.433×106N/m，c=3.5×102（N∙s）/m，μs=0.8。滑履与炭化室地面间静摩擦因数减去动摩擦因数的差值分别取为：0.3，0.25，0.2，0.15，0.1，0.05。采用ADAMS 仿真软件对推焦装置进行动力学仿真获得的推焦装置速度响应曲线如图8 所示。从图8 中可以明显地看出，随着动静摩擦因数差值的减小，推焦装置的黏滑运动现象越来越严重，从最初的只发生在前4s 的时间，到最后在整个10s 时间内均发生了黏滑运动。

图8 静摩擦因数不变而动摩擦因数增大工况下的速度响应曲线Fig.8 The velocity response curves with the condition of con‐stant static friction factor and increasing dynamic fric‐tion factor

4.2 动摩擦因数不变而静摩擦因数减小

推焦系统仿真参数设置为：m=4.12×104kg，v0=0.5 m/s，k1=7.433×103N/m，k2=7.433×103N/m，k3=7.433×106N/m，c=3.5×102（N∙s）/m，μm=0.6。滑履与炭化室地面间的静摩擦因数减去动摩擦因数的差值分别取为：0.3，0.25，0.2，0.15，0.1，0.05。采用ADAMS 仿真软件对推焦装置进行动力学仿真获得的推焦装置速度响应曲线如图9 所示。由图9 可知，在动静摩擦因数差值较大的情况下，推焦装置发生黏滑振动现象的时间比较短；在动静摩擦因数差值不断减小的情况下，推焦装置的黏滑运动现象逐渐增多。

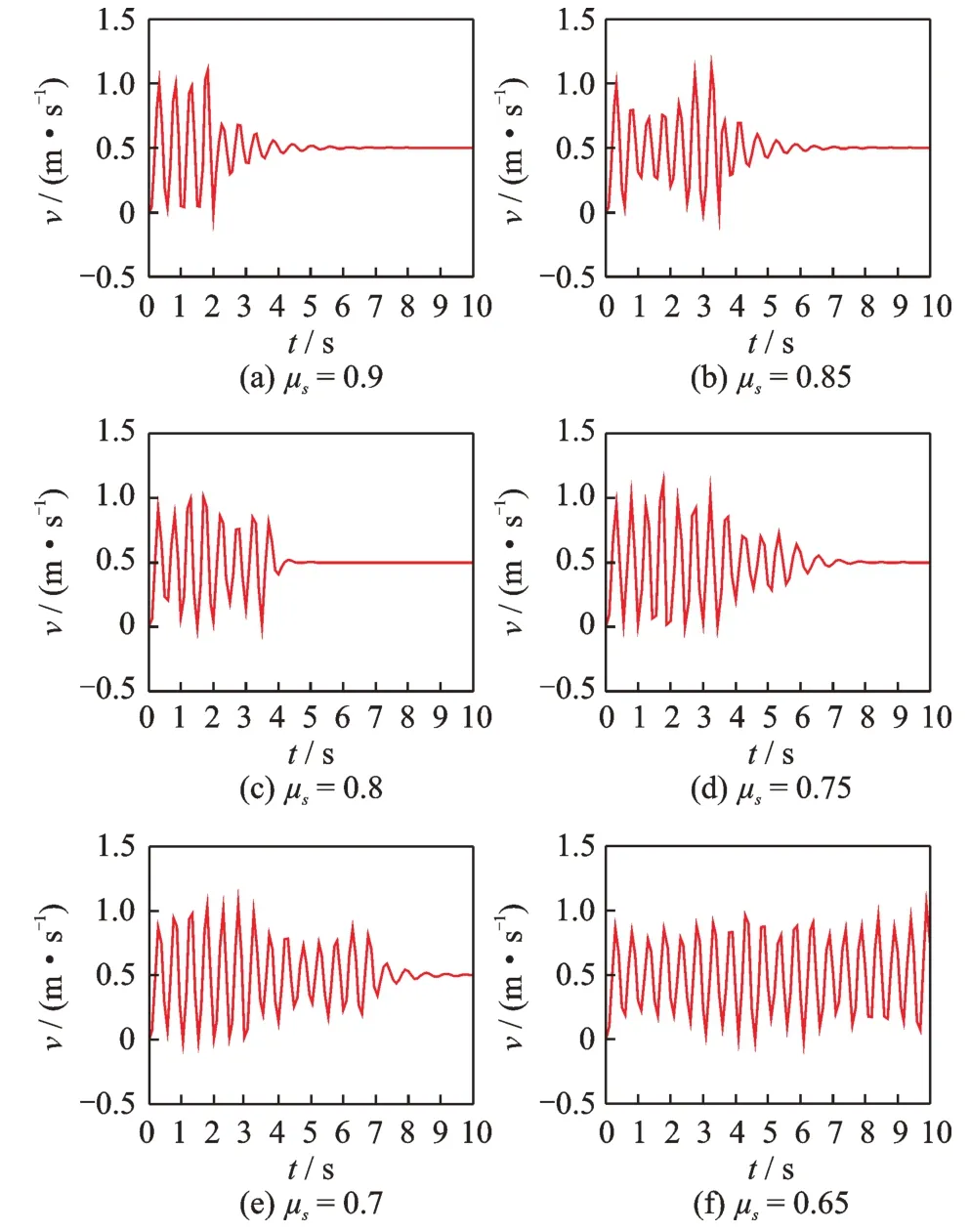
图9 动摩擦因数不变而静摩擦因数减小工况下的速度响应曲线Fig.9 The velocity response curves with the condition of con‐stant dynamic friction factor and decreasing static fric‐tion factor

5 结论

1）利用李雅普诺夫稳定性理论分析了系统的稳定性，计算求得系统的临界失稳速度为0.444 4 m/s。通过理论公式计算了系统的临界黏滑速度，其值为0.564 3m/s。当系统驱动速度小于0.444 4 m/s 时，系统将发生失稳。当系统驱动速度小于0.564 3 m/s 时，系统会发生黏滑运动。

2）动静摩擦因数的差值对系统的稳定性有很大的影响，无论通过增大动摩擦因数还是减小静摩擦因数使得动静摩擦因数差值减小，都能促进系统趋近稳定状态。

3）动静摩擦因数的差值对系统的黏滑运动也有一定的影响，减小动静摩擦因数的差值并不能减轻系统的黏滑运动现象，反而有可能使系统振动加剧。

4）为了提高推焦系统的稳定性，可以通过提高装置的制造和安装精度来提高推焦杆下表面的平面度，使推焦杆的下表面尽可能平行于炭化室地面；也可以采用耐磨和耐热性好、强度高的材料作为滑履底部材料，以减小滑履和炭化室地面的摩擦。为了减轻推焦系统的黏滑运动，可在推焦装置投产前及维护阶段对炭化室地面的耐火砖进行打磨，尽可能使炭化室地面保持平整；改进滑履结构使其可以根据炭化室地面的工况，自动调整滑履底面和炭化室耐火砖的接触面来减小摩擦。