基于全相位FFT 不平衡分析的转子现场动平衡∗

解梦涛，张强波，张霞妹

（中国飞行试验研究院发动机所 西安，710089）

引言

转子不平衡测量分析的精准度与稳定性是其现场动平衡的关键所在［1‐2］，然而对于航空发动机等复杂转子机械的现场动平衡中，通常会由于其空间、环境温度及使用条件等因素的限制难以加装专业动平衡系统及其所需要的振动与转速传感器等测量仪器，而需要借助其自带的振动传感器、转速传感器采集数据，计算出转子不平衡量及动平衡方案。为实现这一目的，笔者建立了基于全相位FFT 的不平衡测量方法与计算模型。

全相位FFT 是在FFT 的基础上发展而来，具备“相位不变形”特点，也可更好地抑制旁谱泄漏，可大幅度地提高幅值及相位计算精度［3‐4］。文献［5］研究表明，在工程中常用的等时采样模式下计算不平衡相位时，全相位FFT 分析方法明显优于互功率法与跟踪滤波法。

首先，建立了基于全相位FFT 的转子不平衡量计算模型，数值仿真结果表明，该模型可准确地计算出模拟信号中各振动分频的振动与幅值；其次，在地面转子试验器上搭建了不平衡测试系统对不平衡测试计算方法进行验证；最后，根据影响系数动平衡法对地面转子试验器进行动平衡操作。结果表明，单次配平后转子最大不平衡振动可下降77.3%，验证了该计算模型的有效性与精度。

1 基于全相位FFT 的不平衡分析

1.1 计算及测量原理

全相位FFT 的实现是在传统的FFT 频谱分析之前增加“全相位预处理”步骤，即在振动数据序列中截取（2N-1）位数据通过卷积窗Wc转换为N位数据，再进行FFT 分析。假设存在原始数据序列x（1-N）～x（N-1），则预处理后的序列y（n），（n=0～N-1）的数学表达式为

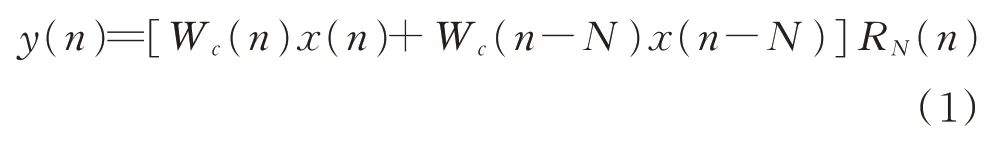
设Wc（-N）=0，RN为矩形窗函数，卷积窗Wc由传统FFT 谱分析所加的窗函数f（需为对称窗）计算得出，设前窗f翻转后的后窗为b，则卷积窗Wc的表达式为

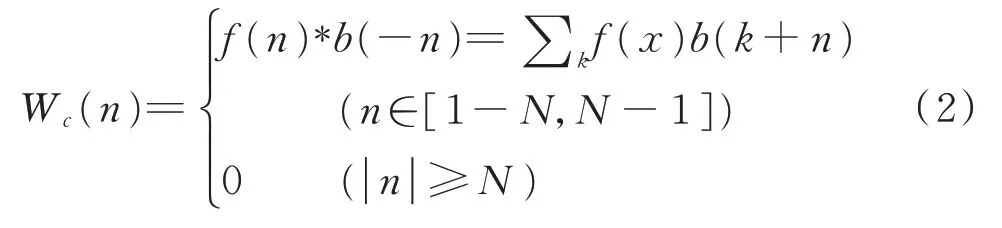
根据式（1）、式（2）最终计算出相对于x（0）数据点处的相位信息，再采用相位差频谱校正方法对幅值、相位等信息进行修正。

不平衡振动幅值与相位的测量计算需要同时利用振动信号与转速信号协调分析获取，其测量原理如图1 所示。其中，振动传感器与转速传感器感应头固定在静子件上，设其周向夹角为θ0，转速传感器旋转盘与转子件固定，设其键相方位与转子上定义的理论配平零位的周向夹角为θ0。旋转过程中当键位通过转速传感器感应头方位时在转速信号中产生高脉冲信号，当转子不平衡方位经过振动传感器方位时在转子基频振动信号中产生振动峰值（振动传感器正向安装方位沿径向向外）。需要计算的相位角为振动峰值点相对于脉冲信号下降沿的滞后角，设为θ。

图1 相位计算原理图Fig.1 Phase calculation schematic diagram

根据全相位FFT 计算原理，可在振动数据序列中以转速脉冲信号下降沿为中心截取2N-1 位数据进行单次振动相位计算，计算所得相位值为90°-θ，其中N为FFT 计算块大小。转子中实际不平衡位置为配平零位向后θ角度处。理论配平零位与配平零位之间的角度差α主要是由测试系统中振动传感器、转换/放大器以及抗混叠滤波器引起的相位平移，而在影响系数动平衡中，相位平移并不会对结果产生影响［6‐7］。

1.2 数值仿真验证

利用Matlab 数值计算软件编写全相位FFT 计算程序，利用模拟振动信号仿真验证其相位与幅值的计算精度。对于由转子不平衡等原因产生的机械振动，信号一般可用正弦函数表示［8‐9］，因此可用式（3）生成一个包含多个不同频率成分和初始相位的复合正弦波形序列

其中：Ai为某一频点振动分量幅值；wi为振动分量频率；φi为振动分量相位。

设模拟信号由5 个振动分量组成，信号时域波形见图1。根据全相位FFT 不平衡计算程序获取振幅谱，以及根据相位差校准法得出的初始相位校正谱和振幅校正谱，其计算结果分别如图2 与表1所示。

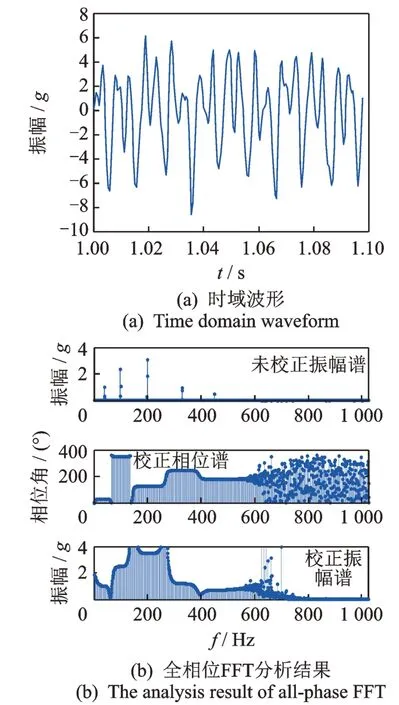
图2 多频振动信号仿真计算结果Fig.2 Simulation results of multi-frequency vibration signal

表1 不平衡振动计算误差列表Tab.1 Calculation error of the unbalanced vibration

由表1 可知，根据全相位FFT 计算获取的初始相位校正谱与振幅校正谱可准确计算出5 个振动分量对应的初始相位值和振幅值，其大小与理论值完全一致，证明了这一分析方法的准确性。

2 不平衡测试系统的搭建与结果分析

不平衡测试系统的搭建及动平衡试验在图3 所示的地面转子试验器平台上展开，其转子系统通过前、后轴轴承支撑，前端带单级悬臂风扇盘，后端通过联轴器与驱动电机相连。

图3 地面转子试验器Fig.3 Ground rotor tester

通过转子结构可推测，风扇盘为转子系统的质量集中点，也是最易产生不平衡质量的地方，因此不平衡测振点选择在前轴承座上，主要采集前轴承座径向振动。根据全相位FFT 计算原理，需要同步采集转子带键相的转速信号方可计算不平衡相位及幅值信息。因此，笔者最终搭建的不平衡测试系统原理如图4 所示，不平衡计算模型可根据采集器同步采集的转速及振动信号计算试验器转子的不平衡振动幅值和相位信息，再进行动平衡计算，给出配重加装方案。

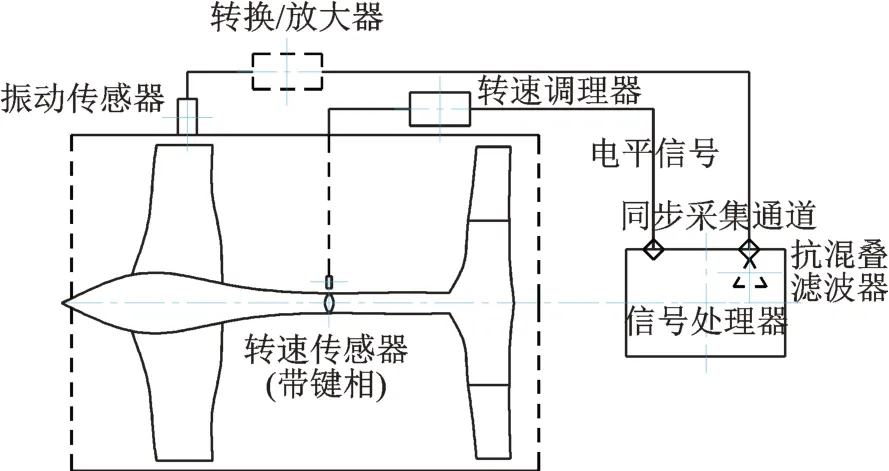
图4 转子不平衡测试系统原理图Fig.4 Rotor imbalance test system

转子不平衡构型的调整是通过在风扇盘上不同相位角的配平孔内加装不同质量的配重螺钉及垫片实现（转子台上沿风扇盘周向均匀分布36 个配平螺栓孔），如图5 所示。

图5 配重及其加装图Fig.5 Balance weight and mounting diagram

在初始无配重构型下试验录取各转速点的转速与振动数据，通过全相位FFT 不平衡计算模型分析各转速点的不平衡振动幅值与相位如图6所示。

在图6（a）所示的转速台阶试验中，每一个台阶处都可检测多个可用于不平衡量分析的计算基准点，如图6（b）所示，每个基准点可计算出1 组不平衡振动幅值及相位数据，分别如图6（c）与图6（d）所示。可知，1 kr/min 以上的每个转速内不同基准点计算的不平衡幅值与相位均非常稳定，表明了所建立分析方法的可靠性。取每个转速点内计算结果平均值作为此转速下的不平衡量，所计算不平衡振动幅值及相位均与转子动力学理论结果趋势相 符［10‐11］。

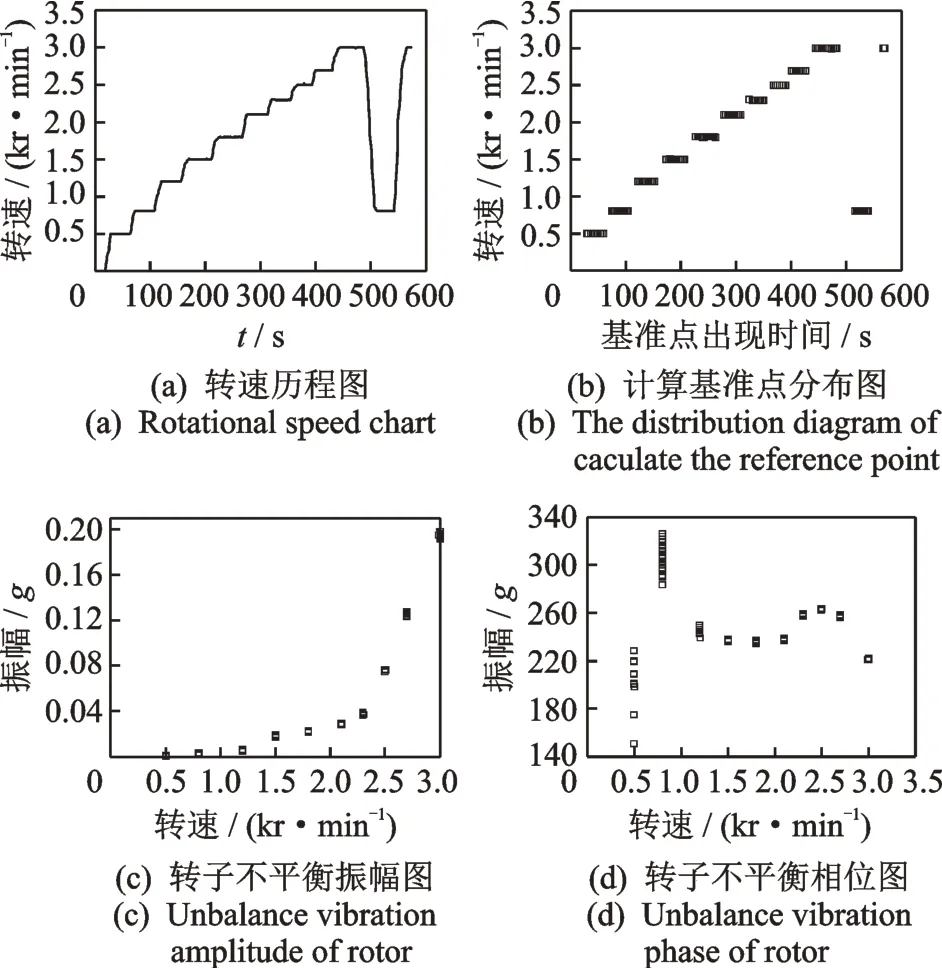
图6 转子系统不平衡特性分析结果Fig.6 Analysis results of unbalanced characteristics of the ro‐tor

3 转子试验器动平衡

首先，根据传统的“三圆法”进行转子动平衡［12］，分别在风扇盘90°，210°及330°相位处加装4.54g 试重。根据“三圆法”作图计算配平方案，结果显示三圆无交点，如图7 所示（图中长度数字仅表示相对比例关系），这说明无法计算出配平方案，需要增加配重质量。

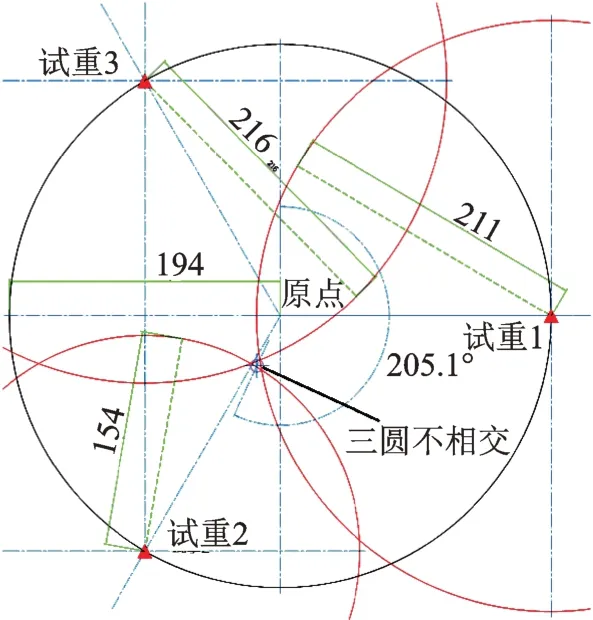
图7 三圆法计算配平结果Fig.7 The balancing scheme calculated by the three-circle method

利用笔者建立的不平衡计算模型根据试验录取数据计算转子不平衡幅频与相频曲线，如图8 所示。可知，不同方位下转子不平衡振动幅值最大仅出现22%的变化量，相位基本稳定不变，表明试重质量确实较小。

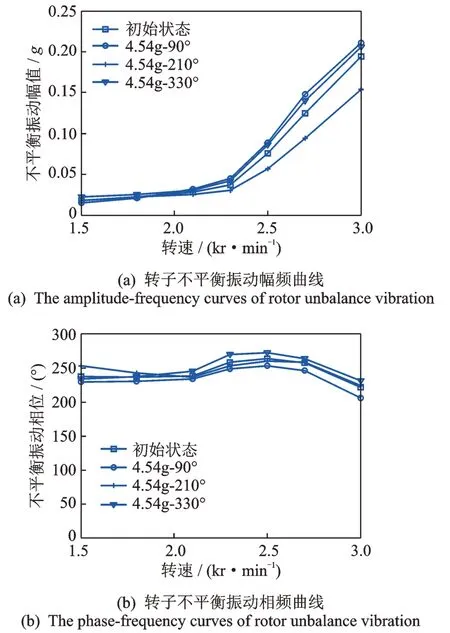
图8 试验获取的转子不平衡振动特性图Fig.8 The unbalance vibration characteristic diagram of the rotor

为表明所建立计算模型的准确性（试重所产生的不平衡振动变化越小对于不平衡计算精度的要求越高，若小试重环境下不平衡计算精度不够，极有可能导致动平衡失败或单次配平后不平衡振动下降幅度很小），笔者直接利用试验数据根据影响系数法计算配平方案。从试验结果可知，3 个方位试重的试验结果中210°方位试重所产生的不平衡振动幅值变化最大，因此选择此组试验数据计算影响系数与配平方案，配平方案的计算采用遗传算法优化方法使各转速点不平衡振动均降至最优值［13‐15］。以1.5 kr/min～3.0 kr/min 之间的所有试验转速点数据为依据计算配平结果，计算获取的配平方案为19.4g‐202.5°，实际加装配重为19.41g‐202°。

配平试验后获取的不平衡振动特性如图9 所示，可知单次配重后转子系统最大不平衡振动值分别下降77.3%，表明所建立的不平衡计算模型及配平算法的有效性与准确性。

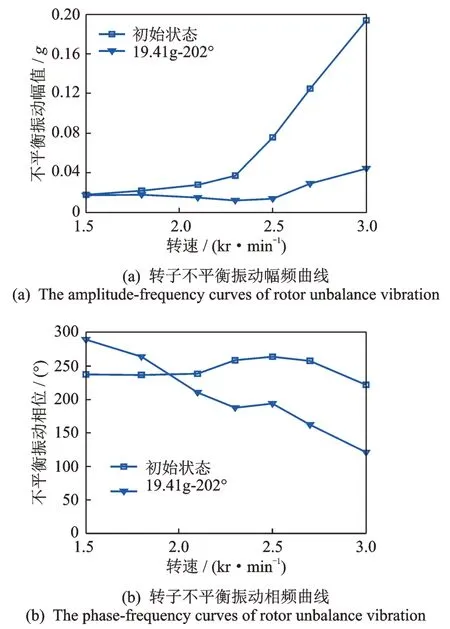
图9 配平前后的转子不平衡振动特性图Fig.9 Unbalance vibration characteristics of rotor before and after balancing

4 结论

1）基于全相位FFT 分析方法建立了转子系统不平衡量的计算模型，试验前的数值仿真结果表明，计算模型可准确地计算出各振动分量的幅值和相位信息。

2）在地面转子试验器上搭建了不平衡测试系统，试验测量结果表明，在转速高于1kr/min 时，所建立的不平衡计算模型可稳定地计算出转子不平衡响应。

3）最终的转子动平衡结果表明，根据所建立计算模型结果可在较轻的试重质量下，单次配平使转子最大不平衡振动下降77.3%，验证了所建立的不平衡计算模型的有效性与准确性，为该计算模型移植到航空发动机转子在线动平衡等复杂工程环境中奠定了基础。