基于复合悬摆减震系统的小雁塔结构仿真分析∗

杨 涛，刘德明，王社良，李彬彬

（1.西安工程大学城市规划与市政工程学院 西安，710048）（2.西安建筑科技大学土木工程学院 西安，710055）

引言

我国有着悠久的文化历史，古塔作为一种历史宗教建筑，是全人类宝贵的历史文化遗产［1］。西安小雁塔是我国密檐式古塔结构的典型代表，具有极高的历史文化价值［2］；然而小雁塔饱经历史沧桑及自然灾害的侵袭，结构内部存在不同程度的损伤，抗灾变能力较差，亟需进行动力灾变保护。因此，对小雁塔的抗灾变保护已成为当前严峻的议题［3］。

近些年来，国内外学者对古塔结构的抗震保护进行了不断的实践和研究。陈平等［4‐5］运用ANSYS对大象寺塔进行了详细的计算与稳定性分析，对古塔结构性能进行综合评判。车爱兰［6］通过有限元数值计算对应县木塔的动力特性和地震响应进行了研究，提出了木结构古塔健康诊断和维修加固方法。Jaishi 等［7］通过对尼泊尔古塔寺庙进行现场环境激振得到其动力特性，对有限元模型进行验证并对其抗震能力进行评估。刘晓莉［8］制作镇国寺白塔的1/40 的缩尺模型，研究了镇国寺白塔传统砌体材料的破坏准则，模拟了镇国寺白塔在汶川地震中的破坏演变过程，但因为模型制作比例较小，相当于实体堆砌，并不能完全体现原型的结构特点。

结构振动控制是一种已被实际验证能够有效减小结构地震响应的新理论、新方法［9‐10］，但国内外学者对SMA 的研究利用主要集中在阻尼器的研发上，较少应用到实际结构工程。笔者设计并制作了形状记忆合金复合悬摆减震系统，为研究SMA‐SP‐DS 在小雁塔结构中的消能减震作用，利用Simulink建立小雁塔结构在设置SMA‐SPDS 下的Simulink仿真模型［11‐13］，对小雁塔模型结构进行地震作用下的仿真分析；结合原型结构现状，基于量纲相似理论，设计制作了一个几何相似比为1/10 的小雁塔模型结构，并进行了小雁塔模型结构振动台试验；将试验结果与仿真分析做对比，验证该仿真模型与计算方法的正确性，并将该仿真模型应用于原型结构，优化并分析了小雁塔原型结构的减震效果。结果表明，SMA‐SPDS 可用于小雁塔结构及其类似砖石古塔结构的减震保护，具有较好的工程应用前景。

1 形状记忆合金复合悬摆减震系统

1.1 SMA‐SPDS 构造设计

利用SMA 丝的相变伪弹性，结合悬摆减震原理，设计了形状记忆合金复合悬摆减震系统，如图1所示。SMA‐SPDS 主要由质量振子、摆杆、单向铰、滑块、SMA 丝、挡板及转向滑轮等构成。

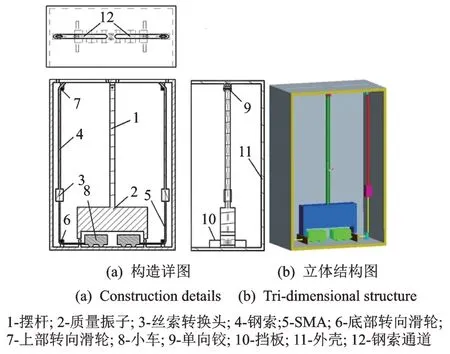
图1 SMA-SPDS 构造图Fig.1 SMA-SPDS structure diagram

1.2 SMA‐SPDS 工作原理

以1 次循环为例来说明形状记忆合金复合悬摆减震系统的工作原理和过程：①当地震作用较小时，质量振子不与滑块接触，可以自由摆动，通过刚性外壁将反向的惯性力作用于结构之上；②当塔身受地震影响较大时，质量振子与滑块一起运动，若结构向右振动时，质量振子将向左摆动，并带动右侧滑块沿水平滑道运动，拉动右侧SMA 丝产生相对位移，此时左侧的SMA 丝仍处于静止状态；当质量振子恢复到平衡位置时，SMA 丝回到初始预拉状态，右侧SMA 丝经历了一个耗能循环过程，形成比较饱满的滞回曲线，实现了对结构的消能减震；同时质量振子的惯性力通过钢索反作用到结构上，对结构的地震响应产生抑制作用，从而使结构的地震响应得到衰减。质量振子向右运动时的原理相同。

悬摆减震体系是一种可设置于古塔结构内部的减震系统，但若单独将悬摆减震体系设置于古塔结构内部楼板上，由于其自身特点对古塔结构起到的减震作用较小。若将悬摆减震体系与SMA 丝相结合，利用丝‐钢索与古塔结构内部连接，研发性能良好的SMA‐SPDS，则可将悬摆减震体系的惯性力通过丝‐钢索传递给古塔结构，同时还能利用SMA‐SPDS 中的SMA 丝提供阻尼，达到消能减震的目的，可明显减小古塔结构的地震响应。

2 设置SMA‐SPDS 的小雁塔结构仿真分析

2.1 小雁塔现场调查

小雁塔为唐代密檐砖佛塔，由塔基、塔身和塔顶三部分组成，原有15 层。塔顶由圆形刹座、两重相轮和宝瓶形刹顶组成，现保留13 层，高为43.38 m。塔身平面呈方形，底边长为11.38 m，塔身略呈梭形，青砖砌成，单壁中空，内壁有登塔砖砌蹬道。2 层以上均逐层递减，高度从3.76 m 至顶层不足1 m。

小雁塔主体结构采用灰砖错缝砌筑，经现场测试灰砖抗压强度在0.71 MPa～1.88 MPa，胶结材料主要为橙黄泥和生石灰，黏性较好，但强度不高。1965 年文物保护部门对小雁塔进行了较大规模的修缮，在第2，5，9 及13 层顶板处浇筑钢筋混凝土梁和楼板，增加其整体性。

2.2 小雁塔试验模型

本试验根据1965 年小雁塔修缮后的现存状况，设计并制作小雁塔模型结构，综合考虑振动台的台面尺寸及承载能力，取尺寸相似系数Sl=，总高度为4 m。模型设计采用欠人工质量方法，将配重设置在塔身墙壁的配重箱内，根据小雁塔原型结构材料的性能，同时兼顾试验的可行性，模型塔身选用经过加工处理的青砖。青砖主要有2 种规格：塔身主体结构用砖为110 mm×50 mm×25 mm；挑檐处用砖为110 mm×50 mm×10 mm。塔身尺寸和整体模型如图2 所示，SMA‐SPDS 在小雁塔内的设置和连接如图3 所示。将SAM 丝通过丝‐索转换接头与钢索连接，经过SMA‐SPDS 底部和顶部的转向滑轮转向后固定于结构的底板处。本次测试采用INV3060A 多通道动态数据采集仪、941‐B 型水平及垂向速度传感器等。

图2 塔身尺寸和整体模型Fig.2 Tower dimensions and overall model

图3 SMA‐SPDS 安装设置图Fig.3 SMA‐SPDS installation setup diagram

由于模型所选材料为砖砌体，其承载力等参数与原型结构基本相同，故可取SE=1。根据Buck‐ingham 理论和量纲分析，计算出模型和原型结构之间的相似关系，从而求得本次试验的各相似系数，如表1 所示。

表1 模型相似关系表Tab.1 Model similarity relation table

2.3 试验方案

根据GB50011—2010（2016 年版）《建筑设计抗震规范》［14］规定，本试验选取了2 条真实强震记录（El‐Centro 波（NS）和江油波（EW）地震记录）和1 条人工波（上海波），进行模拟地震振动台试验。根据试验方案对小雁塔模型结构依次进行8 度小震（0.2g）、8 度中震（0.6g）和8 度大震（0.9g）下的模拟振动台试验，观察设置与未设置SMA‐SPDS 的小雁塔模型结构的试验现象。

2.4 设置减震系统的小雁塔结构仿真过程

笔者假定小雁塔结构在楼板平面内刚度无限大，并不考虑扭转效应，采用层间剪切串联多自由度振动模型进行分析。将设置SMA‐SPDS 的小雁塔结构分为小雁塔主体结构和SMA‐SPDS 两部分考虑，可分别列出各自的运动方程。

2.4.1 小雁塔结构仿真模型的建立

考虑SMA‐SPDS 的作用，小雁塔主体结构运动方程可表示为

其中：P为n×m阶设置矩阵，m为减震装置设置数量，在减震系统设置位置处为1，其余元素为0；f为被动控制力向量，f=和分别为减震装置的位移向量和速度向量。

引入状态向量Z=则小雁塔主体结构状态空间方程为

由此状态方程即可求解小雁塔主体结构相对于地面的位移和速度，而加速度不宜于用Simulink 中的Derivative 求导模块。Derivative 模块的输出属于近似求解，为减小结果误差，结构加速度可由式（3）直接求出

小雁塔主体结构和被动控制力Simulink 仿真模型如图4 和图5 所示。

图4 小雁塔主体结构仿真模型Fig.4 Simulation model of main structure of Xiaoyan Pagoda

图5 被动控制力仿真模型Fig.5 Passive control force simulation model

2.4.2 SMA‐SPDS 仿真模型的建立

SMA‐SPDS 的运动方程为

参照小雁塔仿真模型的建立，可以求得SMA‐SPDS 减震装置的加速度向量表达式为

SMA‐SPDS 的Simulink 仿真模型如图6 所示。

图6 SMA-SPDS 仿真模型Fig.6 SMA-SPDS simulation model

2.4.3 能量反应仿真模型

当设置SMA‐SPDS 的小雁塔结构遭受地震作用袭击时，大部分的地震能量将由减震系统耗散掉［15］，因此减震系统的耗能能力将直接影响小雁塔结构的抗震性能。如果对设置SMA‐SPDS 的小雁塔结构的运动方程在地震持续时间t0内的任一时刻t进行积分，则可简化得到能量平衡方程式［16‐18］为

小雁塔主结构能量反应仿真模型如图7 所示。

图7 小雁塔主结构能量反应仿真模型Fig.7 Simulation model of main structure energy response of Xiaoyan Pagoda

2.4.4 Simulink 主仿真模型

小雁塔减震结构体系Simulink 主仿真模型如图8 所示，该模型由小雁塔主结构、SMA‐SPDS、被动控制力和主结构能量四大子系统构成。M‐加速度、M‐速度和M‐位移分别为小雁塔主结构相对于地面的加速度、速度和位移；S‐加速度、S‐速度和S‐位移分别为减震装置加速度、速度和位移；xg，CF分别为地震加速度和被动控制力；Ek，Ee和Ec分别为小雁塔主结构的动能、变形能和阻尼耗能。

图8 小雁塔减震结构主模型Fig.8 Main model of Xiaoyan Pagoda shock absorption structure

2.5 试验结果

2.5.1 模型结构动力特性

在结构振动台试验中通常采用白噪声扫频的方法来测试结构在不同强度地震作用后的动力特性，因此在试验中每进行一次相同强度的地震作用后，输入加速度峰值为50g的白噪声对模型结构进行扫频，对扫频所得结构加速度响应进行计算，完成小雁塔模型结构的自振频率的求解，结果如表2 所示。

表2 小雁塔模型结构自振频率和周期Tab.2 Natural vibration frequency and period of Xiaoyan Pagoda model structure

2.5.2 模型结构加速度响应分析

在不同地震波的作用下，小雁塔模型结构的加速度响应剧烈区间与输入地震波基本一致，都集中在输入加速度峰值附近。随着地震波强度减弱，结构的响应也逐渐减小。同时在不同地震波作用下，模型结构都会有多个加速度响应值较大的点出现，尤其以江油波表现最为明显。小雁塔模型结构的加速度响应峰值如表3、表4 所示。

表3 无控8 度塔身顶层加速度极值Tab.3 Maximum acceleration of the top floor of the uncontrolled 8‐degree tower g

表4 有控8 度塔身顶层加速度极值Tab.4 Maximum acceleration of the top floor of the controlled 8‐degree tower g

2.5.3 模型结构位移响应分析

小雁塔模型结构顶层的相对位移如表5、表6所示。

表5 无控8 度塔身顶层相对位移最大值Tab.5 Maximum relative displacement of the top floor of the uncontrolled 8‐degree tower mm

表6 有控8 度塔身顶层相对位移最大值Tab.6 The maximum relative displacement of the top floor of the controlled 8‐degree tower mm

2.6 小雁塔模型结构仿真与试验结果对比

根据上述试验结果与用Simulink 仿真方法对小雁塔模型结构仿真分析进行对比，给出小雁塔模型结构在设置和未设置SMA‐SPDS 下的Simulink 仿真与试验结果塔身顶层加速度对比图，用来说明仿真的合理性，如图9、图10 所示。

图9 8 度大震下无控塔身顶部加速度仿真与试验对比图Fig.9 Comparison diagram of acceleration simulation and test on top of uncontrolled tower under 8 degree earthquake

图10 8 度大震下有控塔身顶部加速度仿真与试验对比图Fig.10 Comparison diagram of acceleration simulation and test on top of control tower under 8 degree earthquake

在不同试验过程中小雁塔模型结构随着地震的增大其加速度响应也逐渐增大，塔身顶部从最初的0.6g增加到2.58g。当模型结构中设置SMA‐SPDS后，可以明显减小地震所带来的加速度响应，平均降幅在15%左右，可知本系统在小雁塔结构中能起到较好的减震作用。

由图9 和图10 可以看出，小雁塔模型结构的Simulink 仿真结果与试验结果吻合较好，Simulink仿真方法可以很好地模拟小雁塔模型结构设置与未设置SMA‐SPDS 的地震响应情况，因此可以将上述Simulink 仿真程序应用到模拟小雁塔原型结构的地震响应情况，从而得到在原型结构上设置SMA‐SP‐DS 较为真实的减震效果。

3 小雁塔原型结构仿真分析

3.1 SMA‐SPDS 位置场所优化

笔者研发的SMA‐SPDS 通过控制小雁塔结构的振型来达到减振效果，故设置的SMA‐SPDS 应与结构的振型调谐。通过对该系统配置场所的巧妙选定实现多自由度体系在各个模态单位实现振动控制，减振模态要选择在最有效且不干扰其他模态工作的配置场所。由等效质量概念［19］可知：在某个模态的振动波腹（最大振幅点），等效质量为最小；在某个模态的振动节点（振幅为0），等效质量为无限大。

脉动法在自然环境条件下就可完成对建筑物动力特性的测量，适合历史建筑的动力特性的测试，现场测试结果得到小雁塔结构的水平方向自振频率、阻尼比和振型等动力特性。自振频率和阻尼比如表7所示，现场测试如图11所示，模态振型如图12所示。

表7 小雁塔动力特征值Tab.7 Xiaoyan Pagoda dynamic characteristic value

图11 现场测试图Fig.11 Field test chart

图12 小雁塔模态振型图Fig.12 Modal shape diagram of Xiaoyan Pagoda

现场动力测试可以确定小雁塔原型结构模态控制的SMA‐SPDS 布置位置：控制1 阶模态设置在顶层；控制2 阶模态设置在9 层；控制3 阶模态也设置在顶层，由于顶层已作为1阶模态控制点，因此可另外选择5层作为SMA‐SPDS控制3阶模态的设置场所。

3.2 SMA‐SPDS 参数优化

假设结构具有n个SMA‐SPDS，利用模态坐标建立n个单自由度体系，则附加SMA‐SPDS 的结构运动方程为

其中：Fd为SMS‐SPDS 的作用力向量。

由SMA‐SPDS 得到的作用力向量是位移向量X的函数，传递矩阵设为H，则作用力向量表示为

附带有SMA‐SPDS 的多自由度体系可解耦为单自由度体系，则i阶模态附加SMA‐SPDS 的单自由度体系力学模型如图13 表示，该系统的质量、SMA 刚度和阻尼系数分别设为mdi，kdi和cdi。

图13 i 阶模态的单自由度体系附加减振系统简化模型图Fig.13 A simplified model diagram of vibration reduction system is added to the single-degree-of-freedom sys‐tem of order i mode

通过附加SMA‐SPDS 而产生的作用力Fdi为

由式（8）看出，SMA‐SPDS 充当反馈补偿元素的作用，可以导出传递函数Gdi的表达式为

其中：Gdi为含有该减振系统的i阶模态的传递函数。

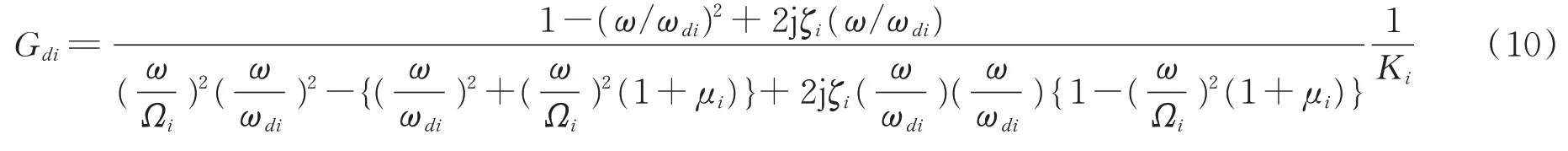
其中：ωdi=ζi=cdi/2mdiωi；μi=mdi/Mi；ωdi，ζi，μi分别为i阶模态减振系统的固有频率、阻尼比和质量比。

形状记忆合金复合悬摆减震系统的最佳设计以定点理论为基础，其核心思想是在有阻尼振动系统的频率响应曲线上，寻找与阻尼无关的特定点，利用特定点进行减振装置的优化设计［20‐21］。本研究利用定点理论对SMA‐SPDS 进行优化设计。

设含阻尼元素ζ的单自由度减振体系，频率传递函数表示为

其 中：C(ω)，A(ω)为不含ζ的关于ω的系数项；D(ω)，B(ω)为包含ζ的关于ω的系数项。

ζ=0 时，频率传递函数为

ζ=∞时，频率传递函数为

相对ζ独立的频率传递函数为

其中：ζ为任意实数。

相对ζ独立的频率传递函数由式（15）决定

当ζ=0或ζ=∞时，频率传递函数的交点与ζ无关，因此该交点就是频率响应曲线的最大值，所确定的ζ值即为最佳阻尼值。在进行SMA‐SPDS 参数设计时，利用定点高度相等，可求出减振装置的最佳调谐值。

对于多自由度体系减振装置最佳设计，利用前文模态分析，可将多自由度减振体系解耦为单自由度减振体系，求出相应的频率传递函数，如式（10）所示。利用式（10）～（14），即可得出i阶模态的单自由度减振装置最佳设计条件，从而可以确定SMA‐SP‐DS 中的主要参数如下。

其中：ωi为i阶模态减振装置固有频率；Ωi为i阶模态结构固有频率；ζi为i阶模态阻尼比；keq为SMA 丝等效割线刚度；l为有效摆长；μi为i阶模态质量比。

各SMA‐SPDS 设置场所确定后，各模态控制下SMA‐SPDS 的目标阻尼比设计为：ζ1=0.11，ζ2=0.078，ζ3=0.05。由式（18）可求得各个模态设置的SMA‐SPDS 的质量比为：μ1=0.03，μ2=0.02，μ3=0.007，从而可 以确定 各SMA ‐SPDS 的参数，见表8。

表8 小雁塔原型结构SMA‐SPDS 参数设计建议值Tab.8 The recommended design value of sma ‐ spds parameters for the prototype structure of Xiaoyan Pagoda

3.3 减振效果

在比较SMA‐SPDS 的优化控制效果时，取结构顶层为研究对象，对其在控制不同阶次振型下的优化控制效果进行分析。由于篇幅限制，此处仅列出8 度大震作用下典型地震波江油波不同阶次振型的小雁塔结构顶层的位移和加速度时程图。

表9 和表10 分别给出8 度大震下El‐Centro 波、江油波、人工波的优化控制1 阶振型、优化控制前2阶振型、优化控制前3 阶振型和无控状态下顶层最大位移与加速度的响应对比，并引入控制效果系数α以反映SMA‐SPDS 对小雁塔原型结构地震响应的控制效果

表9 SMA‐SPDS 优化控制位移效果对比Tab.9 Comparison of optimal control displacement with SMA‐SPDS

表10 SMA‐SPDS 优化控制加速度效果对比Tab.10 Comparison of optimal control acceleration with SMA‐SPDS

其中：|X|1为未设置SMA‐SPDS 的小雁塔结构的地震响应；|X|2为优化设置SMA‐SPDS 时小雁塔结构的地震响应。

由图14～15 分析可知，通过控制不同阶次振型，均可对小雁塔原型结构位移和加速度起到控制效果，且随着控制的阶次提高，对小雁塔原型结构顶层控制效果越显著。由表10 可知，若控制小雁塔原型结构前2 阶振型，在8 度大震作用下，结构的位移响应平均降低32.4%，加速度平均降低31.1%；当控制3 阶振型时，小雁塔结构位移和加速度响应分别平均降低43.8%和43.3%。由此可知，随着控制模态阶次的提高，需要相应地增加SMA‐SPDS 的数量，同时小雁塔结构的控制效果也有明显提高。

图14 江油波优化控制不同振型位移时程图Fig.14 The time-history diagram of optimal control of different displacement modes by Jiang You wave

图15 江油波优化控制不同振型加速度时程图Fig.15 Jiang You wave optimization control acceleration time history diagram of different modes

综合考虑小雁塔实际工程的复杂性、成本控制、可操作性以及小雁塔原型结构的可观光性等因素，笔者建议考虑控制小雁塔原型结构前3 阶振型。

4 结论

1）通过Simulink 建立了设置SMA‐SPDS 的小雁塔仿真模型结构，与振动台试验结果对比，研究了小雁塔模型结构在8 度大震下的地震响应，结果表明仿真分析结果与试验结果吻合较好，说明所建立的设置与未设置SMA‐SPDS 的小雁塔仿真计算模型可以较好地反映试验的真实情况。

2）将小雁塔模型结构Simulink 仿真模型应用到小雁塔原型结构的模拟计算，进行了小雁塔原型结构在8 度小震、中震及大震下的模拟分析。结果表明：当小雁塔原型结构设置减震系统后，各阶频率均有所提高，说明SMA‐SPDS 可以提高原型结构的整体抗震性能；同时，SMA‐SPDS 对减小小雁塔结构的地震响应具有明显的作用，且随地震强度的增加，减震效果越明显。

3）针对小雁塔原型结构，对SMA‐SPDS 的参数、布置位置等进行了优化设计，对比分析了小雁塔原型结构中布置SMA‐SPDS 优化前后的地震响应情况。结果表明，通过控制不同阶次振型，均可对小雁塔原型结构位移和加速度起到控制效果，且随着控制的阶次提高，对小雁塔原型结构顶层控制效果越显著。当控制3 阶振型时，小雁塔结构位移和加速度响应分别降低43.8%和43.3%，优化效果显著。

4）形状记忆合金复合悬摆减震系统对小雁塔结构的保护，严格遵循古塔结构抗震保护的“最小干预”原则，可有效减小塔体的地震响应，对于类似古塔的抗震保护具有一定的参考价值和工程意义。