统计时频谱驱动的高速自动机损伤预示方法∗

王宝祥，潘宏侠

（1.淮阴工学院机械与材料工程学院 淮安，223003）（2.中北大学机械工程学院 太原，030051）

引言

当前，在部队训练趋于实战化和常态化大背景下，高强度训练对兵器装备服役性能提出了更高要求，兵器装备安全性和可靠性日益受到关注。高速自动机是武器系统重要组成部分，由于在恶劣的工作环境中遭受复杂多变的工作载荷，各组成元件在设计、制造、装配过程中存在的缺陷逐渐暴露出来，武器系统卡滞、磨损等故障时有发生。如何保障武器装备的服役性能是一个需要迫切解决但又具有挑战性的课题。

枪弹击发时，在火药燃烧产生的高压气体冲击下，系统各组件在极短时间内完成了复杂的运动形态转化过程，并伴随着一系列剧烈的冲击和振动。高速自动机复杂运动形态的响应信号是一系列非平稳短时瞬态冲击序列，其中既包含组件早期损伤的微弱状态信息，也混有大量背景噪声及其他干扰成分，导致武器系统早期故障特性不够明显。现有的智能故障诊断方法主要解决分类问题，需要大量的故障样本训练分类器，而实际应用中高速自动机历史故障样本却很难收集［1‐3］。统计多变量过程控制方法使用设备正常样本建立参照模型，通过统计未知状态样本与参照模型的偏差反映设备服役性能演化轨迹，同时估计出设备安全服役的参考阈值用于服役性能控制，有利于早期故障检测。Yu［4］提取了滚动轴承服役性能演化过程的多特征参数，建立了融合多特征局部信息的局部保持投影模型（locality preserving projections，简称LPP），检测到轴承早期损伤特征。为监测大型回转支承周期故障，Žvokelj等［5］利用集成经验模态分解（ensemble empirical mode decomposition，简称EEMD）将原信号分解到多尺度上，构建了每个尺度的独立成分分析（inde‐pendent component analysis，简称ICA）模型，显著增强了回转支承故障时的周期性冲击特征。Lu 等［6］采用主成分分析（principal component analysis，简称PCA）融合回转支承的多特征参数，建立了优化最小二乘支持向量机模型（least squares support vector machine，简称LSSVM），预测了回转支承性能退化趋势。针对轴承退化的非高斯过程特性，Jin 等［7］计算了ICA 模型的高阶累积量，准确反映了轴承性能演化过程。Rai 等［8］构建了K 中心点聚类模型识别正常状态与故障状态聚类中心，定义了置信值曲线量化了两者之间的偏离程度，用于跟踪轴承退化过程。然而，上述方法仅能针对单一模态数据建立参照模型，相对于融合两种模态相关信息的规范变量分析（canonical variate analysis，简称CVA）模型，在检测冲击类故障时，容易受到系统瞬时冲击不确定性的影响［9］。CVA 是一种基于最小状态空间的动态监测方法，主要用于缓变过程故障监测［10‐11］。若对高速自动机瞬时冲击类故障进行动态监测，则还应考虑到以下几个方面：①瞬时冲击故障与缓变过程故障不同，由于组件间存在间隙或者自由行程，剧烈冲击导致信号幅值骤然上升，之后迅速衰减，在信号幅值上不是一种典型的渐变过程；②早期微弱损伤一般不会引起信号幅值明显上升，单纯针对时域或者频域特征进行监测往往不易奏效；③针对瞬时冲击损伤预示，需要一种能够密切跟踪系统瞬时特性的时变特征参数。

基于以上认识，提出了一种统计时频谱驱动的高速自动机损伤预示方法。通过短时傅里叶变换计算了瞬时信号的时频分布图，提取冲击信号的瞬时频率特征这一时变参数，构建基于核密度估计的CVA 监测模型，并与动态PCA 模型进行比较，验证了该监测方法对瞬时冲击故障的有效性。

1 理论与方法

1.1 瞬时频率

瞬时频率描述了非平稳瞬时冲击信号的频谱峰值随时间的变化过程，它定义为信号时频分布的频率平均［12‐13］。若以fs表示瞬时频率，则有

其中：P(t，f)为信号的功率谱，是关于时间和频率的二维分布函数，可通过对信号进行短时傅里叶变换得到。

短时傅里叶变换采用滑动窗口将原信号分为一系列信号片段，并对每段信号做傅里叶变换，可以捕捉到冲击信号中有关早期故障的细节信息。

1.2 规范变量分析

规范变量分析方法是一种考虑时间序列相关性的动态维数减少方法，通过寻找一种线性组合使得两组变量间的相关性达到最大，从而提取两组变量间的关联信息，减少设备运行过程中不确定性的影响。基于规范变量分析的统计过程控制方法采用设备正常状态数据建立参照模型，生成健康阈值，然后将观测到的未知状态数据沿参照模型投影，统计数据投影和参照模型间的偏差作为健康指标，当其越过安全阈值则表明监测的系统发生故障。现假设有一观测序列xt，考虑到时间序列在未来时刻p与过去时刻f间的相关性，对xt进行扩展后生成过去和未来向量xp，t和xf，t［10，14］

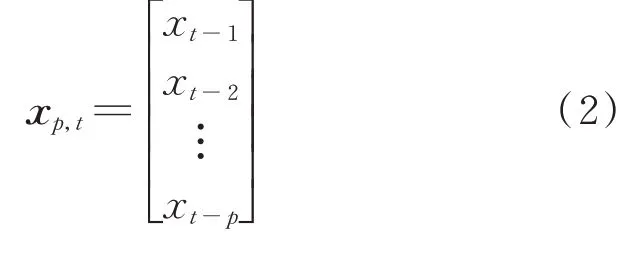
在进行最大相关性分析前，先对数据进行标准化处理

将标准化后的向量按列排列后生成过去和未来数据矩阵Xp和Xf

其中：M=N-f-p+1；N为数据长度。

Xp和Xf方差和协方差矩阵可表示为

为揭示变量间潜在关系，对Hankel 矩阵进行奇异值分解

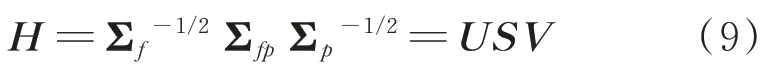
其中：S为对角矩阵，其对角元按照降序排列。

若将前r个特征值对应的特征向量定义为维数减少矩阵Vr，则状态空间和残差空间的投影矩阵J和L分别表示为

则过去数据矩阵Xp在状态空间和残差空间投影Z和E为

HotellingT2和平方预测误差（squared predic‐tion error，简称SPE）是分别定义在状态空间和残差空间上的两种互补统计量，可用于度量子空间中的信息变化量

其 中：zi，t和ei，t分别是矩阵Z和E中的列向量元素。

1.3 核密度估计

核密度估计无需先验假设就可以计算任意样本分布的概率密度函数，常用于设置健康指标的安全阈值［15］。对于随机变量x，其小于给定值s的概率可表示为

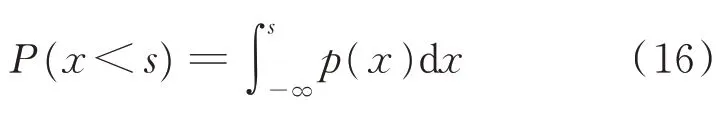
其中：p(x)为变量x的概率密度函数，通过核函数K(∙)计算。

其中：h为宽度参数。

若以μ表示变量的标准差，其最优值可计算为

由式（17）可估计出统计量Tt2和Qt的概率密度函数。若用Tucl和Qucl分别表示两种统计量的控制限值，在置信度为α时，控制限值可通过下式求解

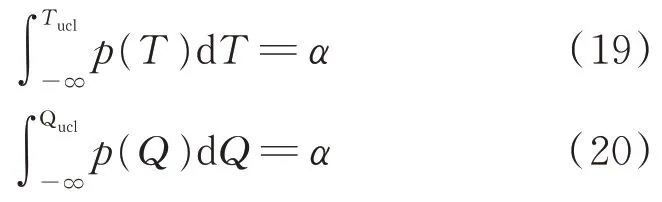
α一般取值0.99。由于两种统计量互补性可知，任一统计量越过安全阈值则可认为系统故障。

1.4 高速自动机损伤预示方案

统计时频谱驱动的高速自动机损伤预示包含特征提取、离线建模和在线监测3 步：

1）计算高速自动机正常状态信号的时频分布图，提取瞬时频率特征，组成多变量特征集合；

2）训练CVA 模型，用核密度估计确定高速自动机健康状态参考阈值；

3）提取观测信号的瞬时频率特征，计算特征投影的偏差统计量，与参考阈值进行比较识别瞬时状态。

高速自动机损伤预示方案如图1 所示。

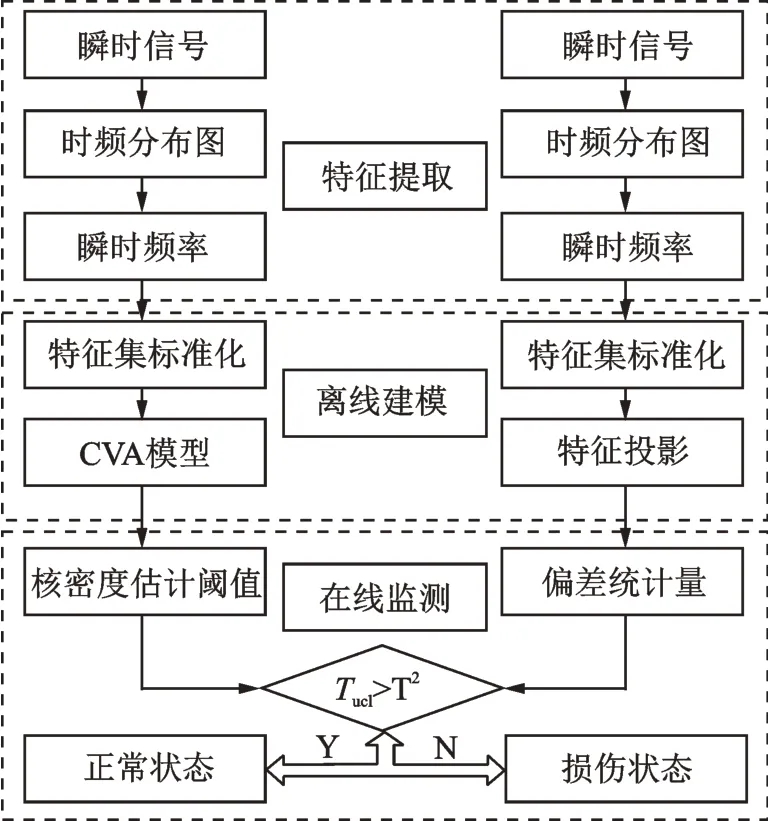
图1 高速自动机瞬时损伤预示方案Fig.1 The scheme for damage prediction of high-speed au‐tomata

2 实验与结果

2.1 数据采集

为了检测瞬时冲击类故障，实验收集到高速自动机在3 种不同状态时的瞬时冲击信号，包括正常状态、闭锁片圆角附近深度为2 mm 的裂纹故障以及枪机圆角处深度为1.5 mm 的裂纹故障。这是由于火药燃烧产生的高压气体一部分为弹头提供动能，一部分通过枪管前端导气管推动枪机后坐，当复进簧受压后再推动枪机复进。在高温高压恶劣环境下，闭锁片是比较容易出现损伤的组件，后坐时枪机受到巨大冲击力也容易产生裂纹。高速自动机冲击试验平台如图2 所示。因枪弹击发时和枪机后坐时存在剧烈冲击振荡，以枪管指向作为x轴方向，将两个加速度传感器分别粘贴在自动机尾部和机匣上方，采用LMS 数据采集系统记录自动机全行程的瞬态冲击信号，采样频率设置为204.8 kHz。本次实验选择后座测点处沿x轴方向的冲击信号进行分析，每种状态包含4 个样本信号构建数据矩阵。正常状态下获取的五连发瞬态冲击信号以及3 种不同状态信号如图3 所示。3 种状态的冲击信号具有相似的波形，且每次冲击持续的时间极短，只有10 ms。

图2 高速自动机实验平台Fig.2 High-speed automaton test rig

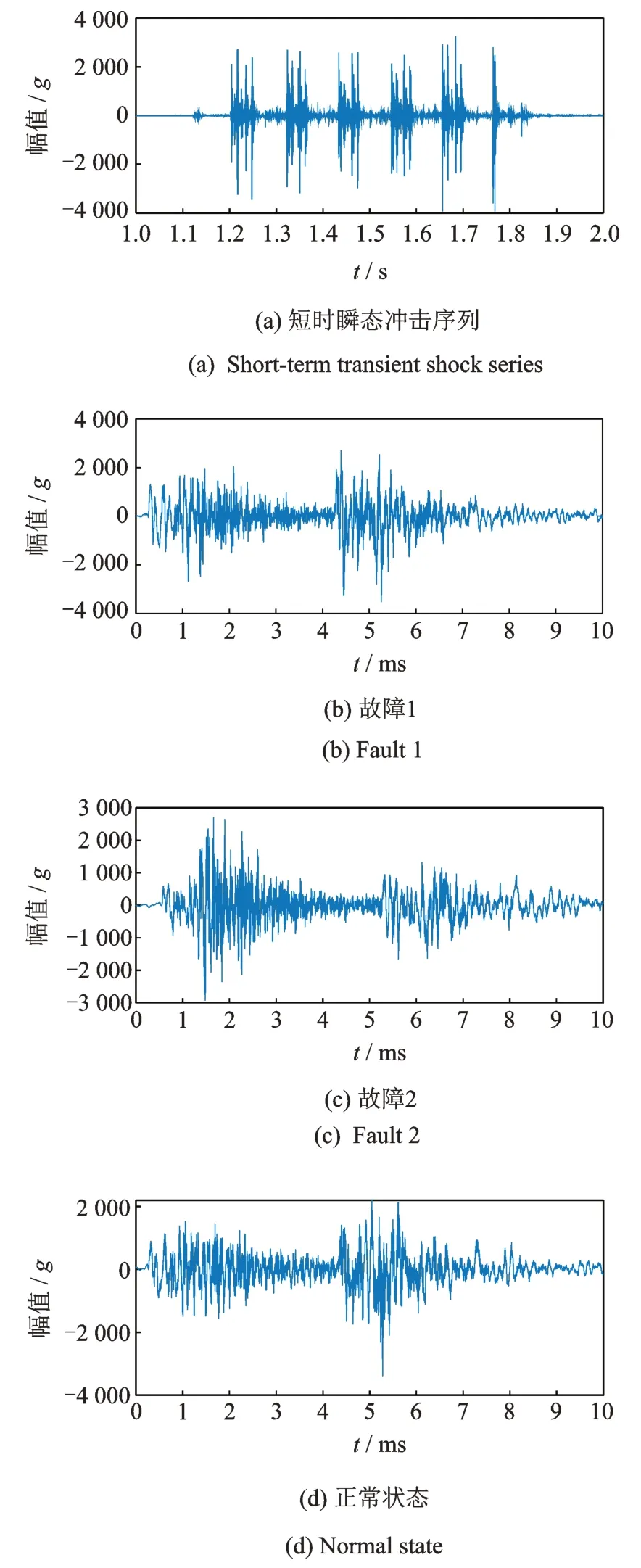
图3 短时瞬态冲击信号Fig.3 Short-term transient shock signals

2.2 实验结果

为提取非平稳冲击信号蕴含的潜在模式，采用短时傅里叶变换对信号进行时频变换，得到正常状态和故障状态的时频分布图，如图4 所示。其中，窗口长度为512，相邻信号段重叠为511。由图可知，正常状态下冲击信号能量主要集中在低频部分，而故障状态时冲击信号的能量主要集中在高频部分。鉴于正常信号和故障信号呈现的能量分布差异，可以提取信号的时频谱特征表征高速自动机不同运行状态。如图4 所示，在冲击附近具有较高瞬时频率值，能够反映不同状态时信号频率成分随时间的变化过程。因此，提取每种状态信号瞬时频率建立数据矩阵，以正常状态的瞬时频率特征集训练CVA 参照模型，以核密度估计方法生成参考阈值。CVA 包含3 个参数，即过去与未来时间序列长度p和f，保留的规范变量个数r。一般取p=f，这两个参数可通过计算训练数据的自相关函数来确定［10］。经过实验研究后将其取值为8，足以反映瞬时信号的动态特性。参数r可由多种方法确定，如奇异值分析法。考虑到状态空间和残差空间的互补性使得检测结果对参数r不敏感［15］，取r=15。若状态空间中的统计量超过安全阈值即表明系统出现故障。将故障信号的瞬时频率特征集投影到CVA 模型，并统计状态空间中瞬时频率变化量，产生如图5 所示故障检测结果。

图4 冲击信号时频谱及特征Fig.4 Time-frequency spectra of shock signals and their fea‐tures

如图5（a）所示，高速自动机正常状态的瞬时频率统计量随时间上下波动，整个瞬态过程都位于参考阈值之下。故障1 发生后，统计指标表示的瞬时频率变化量在组件撞击时陡然增加，越过参考阈值后达到峰值。这表明，对瞬时频率特征的变化量进行统计可以提取正常与故障冲击信号的本质特征，准确区分了不同状态下的潜在运行模式，实现了对瞬时冲击类故障的检测目的。如图5（b）所示，在故障2 发生后其瞬时频率变化量的峰值超过参考阈值，检测结果清晰地揭示了故障发生前后频率随时间的变化规律，再次证明了所提出的方法对检测瞬时冲击故障的有效性。本次实验结果也显示，不同于对时域信息变化的检测方法，该方法从冲击信号时频谱上提取瞬时频率，对频谱信息随时间的变化轨迹进行统计，可以提高对微弱故障的检测效率。这是因为，早期微弱故障在幅值上变化往往不够显著，但是可通过频率分布的细微变化体现出来。

图5 CVA 瞬时损伤监测Fig.5 Monitoring of transient damage using CVA

2.3 方法比较

为了比较不同方法对瞬时冲击故障的检测性能，采用文献［16］中的矩阵增广方法建立了一种动态PCA 模型，其对上述两种瞬时故障的检测结果如图6 所示。其中保留的主成分个数为15，相关时间序列长度为8，与前文保持一致。图6 显示，高速自动机正常状态下的瞬时频率变化量低于安全阈值，故障发生后对应的瞬时频率高于安全阈值，动态PCA 成功检测到两种系统异常带来的频谱提升。将动态PCA 与CVA 检测结果进行比较，可发现后者建立的参考模型及阈值更加稳定，正常状态下健康指标远低于安全阈值，瞬时冲击对监测结果的不确定性影响较小。另一方面，后者更能反映冲击故障时系统的动态特性，突出了瞬时冲击处的频谱峰值特征。这是由于动态PCA 模型建立在单一特征集上，而CVA 模型通过最大化两组特征的相关性获取对瞬时冲击信号特征信息的一致理解，能够减少瞬时冲击故障时的不确定性影响［9］。

图6 动态PCA 瞬时损伤监测Fig.6 Monitoring of transient damage using dynamic PCA

3 结论

1）统计时频谱驱动的损伤预示方法对瞬时冲击类故障是有效的。该方法从对微弱损伤更加敏感的频谱分布图提取瞬时频率特征，能够准确揭示瞬时冲击信号频率随时间的变化规律，这是统计模型实现损伤预示的基础。

2）CVA 和动态PCA 模型都能有效检测到瞬时冲击故障，由于CVA 提取两个特征集的共同信息，因此能够减少瞬时冲击故障的不确定性影响。

3）高速自动机的运动形态具有多行程特点，其响应信号是一系列短时瞬态冲击序列。未来应该发展兼顾高速自动机各行程特点的全行程状态监测方法。