基于多通道时频域信号的卷积神经网络智能故障诊断技术
孙仕鑫, 高 洁, 王 伟, 杜劲松, 杨 旭
(1.中国科学院沈阳自动化研究所, 沈阳 110016; 2.中国科学院机器人与智能制造创新研究院, 沈阳 110169; 3.中国科学院大学, 北京 100049; 4.辽宁省智能检测与装备技术重点实验室, 沈阳 110179)
滚动轴承作为旋转机械如齿轮箱的关键部件[1],长时间工作在嘈杂的环境中,不可避免地会出现各种故障。为防范可能存在的隐患,最常见的方法是通过分析其振动信号来进行早期的故障诊断。传统智能故障诊断算法主要包括特征设计、特征提取和选择、状态识别[2]。而特征设计需要专家知识,并且设计的特征具有专一性,即在此数据集上设计的特征不适用于另一数据集,因此传统智能故障诊断算法具有特征设计复杂、不利于推广等缺点。近年来,深度学习的崛起为克服上述缺点提供了新的方法[3]。深度学习是一种端到端的学习方法,不需要专家知识,原始数据直接作为输入,分类结果作为输出,省去了繁杂的特征设计,且利于推广,因此在滚动轴承故障诊断领域中广泛使用。
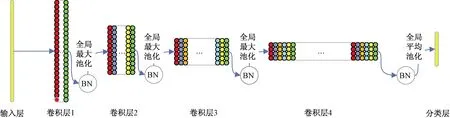
BN是批标准化层图1 卷积神经网络结构Fig.1 Convolutional neural network structure
然而,在实际工业环境中,算法不能学习到所有负载下的健康状态特征,例如在极端情况下,算法只能在1 hp(马力,horsepower)负载下训练,在实际测试时,却需要在3 hp负载下有效识别健康状态,所以就要求算法有很强的负载域适应能力。因此,中外专家学者相继提出了在变负载下的滚动轴承故障诊断算法。Jiao等[4]提出了双级对抗域自适应网络(double-level adversarial domain adaptation network,DL-ADAN),该模型由基于深度卷积网络的特征提取器、域识别器和两个标签分类器组成,用于识别跨领域的故障状态。Qiao等[5]提出了基于卷积神经网络和长短期记忆神经网络的时频双输入模型(time-frequency dual-input model based on a convolutional neural network and a long-short term memory neural network,FT-WConvLSTM),此模型的卷积层和长短期记忆层分别提取时频图像的空间特征和时域信号的序列特征,最后的密集层被用于故障分类。Li等[6]提出了深度平衡域自适应神经网络(deep balanced domain adaptation neural network,DBDANN),多个卷积层提取特征后,采用多层平衡域自适应方法减小不同域之间边际概率分布和条件概率分布的差异。祝道强等[7]提出了一种基于一维卷积神经网络的变负载适应轴承故障诊断模型,并在两种近邻负载条件的轴承数据构成的变负载数据集上取得了较好的诊断效果。
上述算法在变负载下的滚动轴承故障诊断方面都取得了不错的效果,但由于时域信号的特征规律不明显,以及网络丢失重要特征的缘故,使得诊断精度仍有提升的空间。针对上述问题,提出了基于多通道时频域信号的卷积神经网络算法(convolutional neural network based on multi-channel time-frequency signals, CNN-MCTFS),用于诊断滚动轴承在变负载下的健康状态。该算法只在源域下训练,无需目标域数据的参与,即可在目标域下得到良好的诊断效果。此算法的贡献如下:
(1)卷积层采用空洞卷积,也就是向原卷积核中填充空洞,以扩大卷积核的感受野。
(2)全局最大池化替代最大池化,在全局范围内提取卷积层的最大激活,而非有限宽度的滑动窗口中的最大激活。
(3)使用不同小波的离散小波变换将时域信号变换为多通道时频域信号,其中不同的小波提取不同的特征,可以为卷积神经网络提供更丰富的健康状态信息。
1 卷积神经网络的搭建
卷积神经网络(convolutional neural network, CNN)由输入层、卷积层、批标准化层、池化层、分类层组成,如图1所示。
1.1 卷积层(空洞卷积)
卷积层(convolutional layer,Conv)的每个卷积核使用相同的数值来提取输入的局部特征[8],如果感受野越大,也就是卷积核越宽那么卷积的输出包含的信息就越多[9]。VGGNet模型中,三层3×1Conv的感受野相当于一层7×1 Conv,因此可以通过加深网路获取更大的感受野,但CNN层数过深在训练时容易出现退化现象[10],降低了网络的分类精度。如果在Conv中采用7×1宽度的卷积核,虽然扩大了卷积核的感受野,但也增加了计算量。为此,可以使用空洞卷积,也就是向原卷积核中添加空洞以扩大卷积核的宽度,从而扩大卷积核的感受野。如图2所示,空洞卷积核的宽度由空洞率(dilation rate)控制,则空洞卷积核的宽度为
Kernel+(Kernel-1)(Dilationrate-1)
(1)
式(1)中:Kernel是原卷积核的宽度。
1.2 池化层(全局最大池化)
池化层的作用就是在提取那些被激活成较大值的重要特征,用于削减特征尺寸,以及保持平移不变性。然而,最大池化只会提取被固定宽度的滑动窗口内的最大激活,但如果滑动窗口中都是最大激活,它们只能选出其中之一,而其他值则被抛弃,如图3(a)所示。因此,在每一Conv后,采用全局最大池化[图3(b)]代替最大池化,用于提取全局范围内的最大激活,即无需考虑位置,也可保留更多的重要特征。
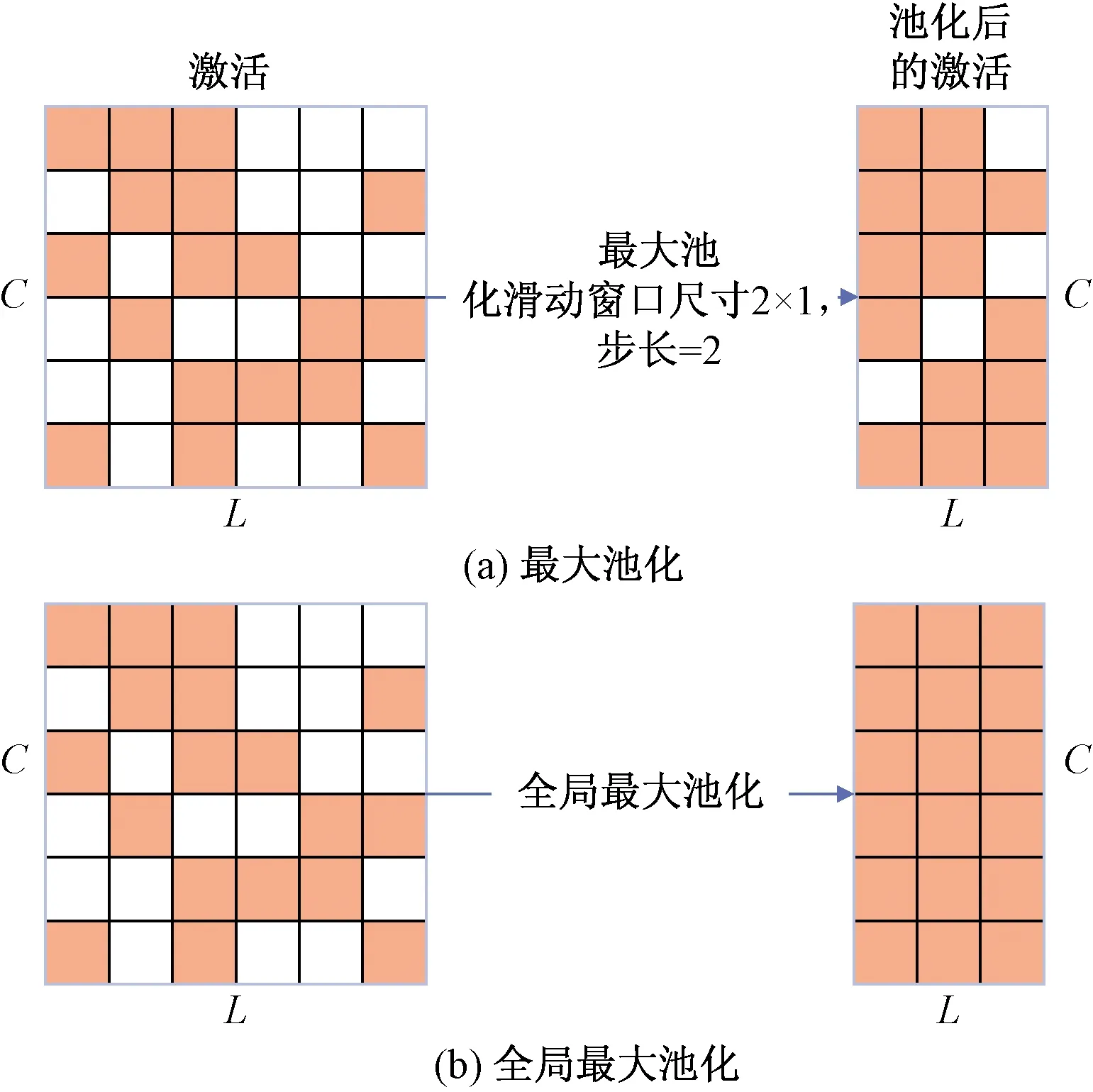
图3 两种池化操作Fig.3 Two pooling operations

(2)
式(2)中:activation和Activation分别是池化前的激活和池化后的激活;GlobalMaxPool(·)是全局最大池化;C和L分别是通道数和长度。
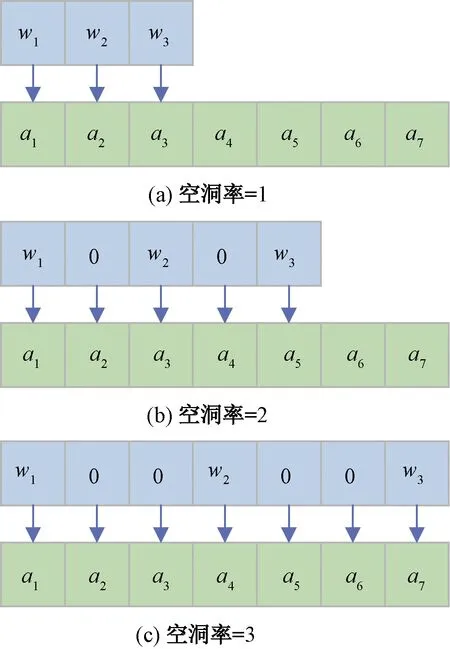
w和a分别是卷积的可学习参数和输入值图2 空洞卷积Fig.2 Dilated convolution
1.3 卷积神经网络的结构
在每一Conv之后,激活函数之前放置批标准化层,以加速网络收敛速度,并且起到正则化的作用,防止网络过拟合。接着放置激活函数,文中激活函数选择了ReLU函数,相比Sigmoid和Tanh等函数,此函数不仅克服了梯度消失等问题,并且加快了网络的训练速度。再放置全局最大池化用于提取全局最大激活,以及削减特征维度。选择4层Conv,每一Conv的卷积核都相当于是7×1的感受野,这样不仅可以充分学习到信号的健康状态特征,而且也无需耗费太多计算量。最后全局平均池化将每一通道挤压为每一点,用于最终的分类,并且无论输入信号的长度或者分解层数是多少,全局最大池化和全局平均池化的使用可以令网络按照表1所示参数搭建。分类层采用Softmax函数进行分类,以判断信号的健康状态。
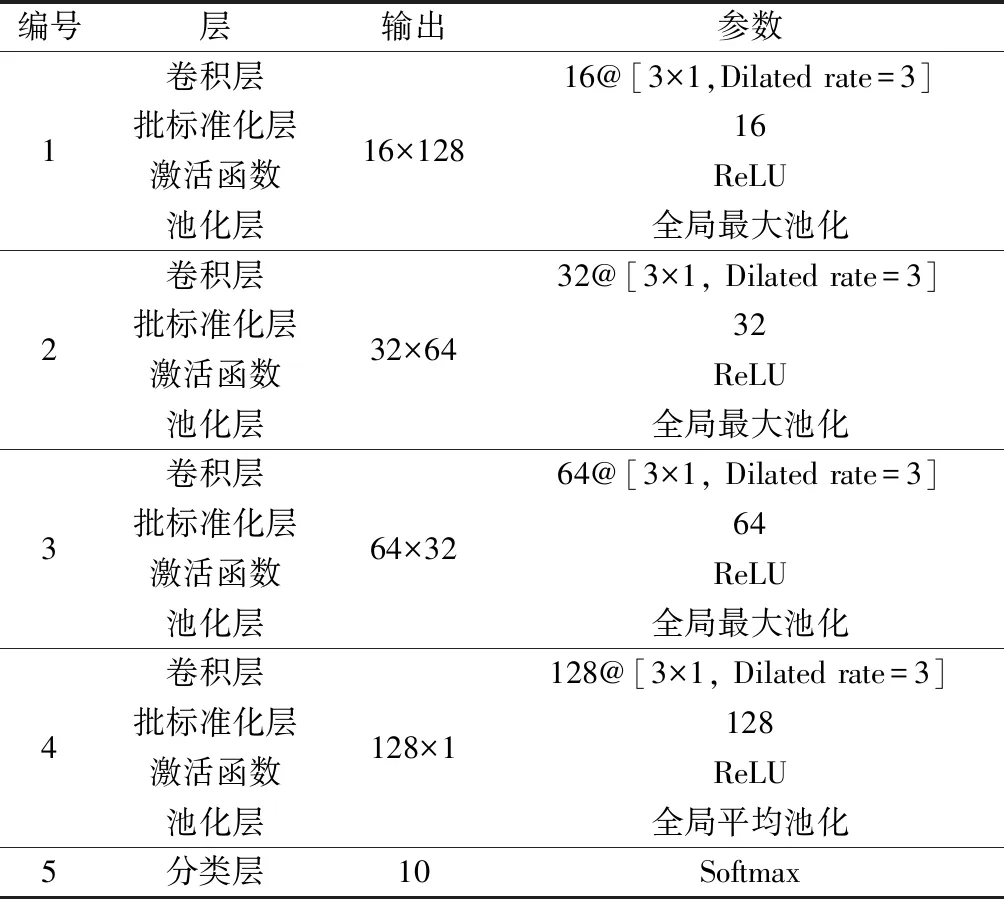
表1 卷积神经网络参数
2 多通道时频域信号的构造
振动信号在时域下呈波形,特征规律不明显,为了凸显滚动轴承的健康状态特征,可以通过傅里叶变换或离散小波变换将时域信号转换到频域或时频域。其中傅里叶变换以三角函数为基拟合时域信号,考察的是信号的整体频域特征,对于平稳信号具有良好效果,而在非平稳信号上的效果较差。离散小波变换利用小波,通过伸缩、平移等运算对信号进行多尺度细化分析,可以很好地分析非平稳信号,从时域信号中提取时频信息。并且不同的小波从时域信号中提取的时频信息不同,多种小波可以提供更多样的时频信息,以便CNN可以抽取更抽象的健康状态特征。
设f(x)是时域信号,ψ(x)为小波,则连续小波变换(continuous wavelet transform, CWT)为

(3)
式(3)中:s是尺度因子;τ平移因子; *表示复共轭操作。离散小波变换是把尺度因子s与平移因子τ离散化,即在离散点取值[11]为

(4)
式(4)中:s≠1;τ是常数。相应的离散小波变换(discrete wavelet transform,DWT)为

(5)
尺寸为(C=1,L)的时域信号首先经过level级DWT后得到近似值Alevel(level表示分解层数)和细节系数(Dlevel,Dlevel-1,…,D1),再将它们串联在一起得到尺寸为(C=1,L′)的时频域信号[Alevel,Dlevel,Dlevel-1,…,D1]。
然而,有多种可用于离散小波变换的小波,例如daubechies(db)小波、symlets(sym)小波、coiflets(coif)小波、haar小波、dmeyer(dmey)小波、biorthogonal(bior)小波和reverse biorthogonal(rbio)小波。因此,在进行离散小波变换时,为了保证变换前后信息的保留,避免在变换后引入误差,应选用重构误差低的小波[12-13]。重构误差为
error=sum(|f(x)-iDWT{DWT[f(x),ψ(x)]}|)
(6)
式(6)中:DWT和iDWT分别是离散小波变换和逆离散小波变换;sum(·)表示元素求和操作;|·|表示求绝对值操作。挑选4.1节数据集A的10 000个样本用于求取重构误差,则各小波的重构误差如表2所示(只列出有限个小波的重构误差,并且level=1)。

表2 各小波的重构误差
从表2可以看到,rbio2.2、bior2.2、coif1和db3小波的重构误差较低且相近,由它们得到的多通道时频域信号,比只使用rbio2.2小波得到的时频域信号,蕴含着更加多样化的健康状态信息。虽然db5小波的重构误差也和这些小波相似,但由db5小波变换得到的时频域信号尺寸L′与它们不同,如果通过伸缩操作使得尺寸L′强行一致,可能会缺失信息或引入错误信息,故放弃使用。所以,rbio2.2、bior2.2、coif1和db3小波分别对时域信号进行level级(最佳分解层数之后由实验选择)离散小波变换,得到4种不同的时频域信号,再将这4种不同的时频域信号在维度C上组合成尺寸为(C=4,L′)的四通道时频域信号,如图4所示。具体步骤如下。

图4 多通道时频域信号Fig.4 Multi-channel time-frequency signals
3 滚动轴承智能故障诊断算法流程
基于上述阐述,建立起滚动轴承智能故障诊断流程图,如图5所示。具体步骤如下。
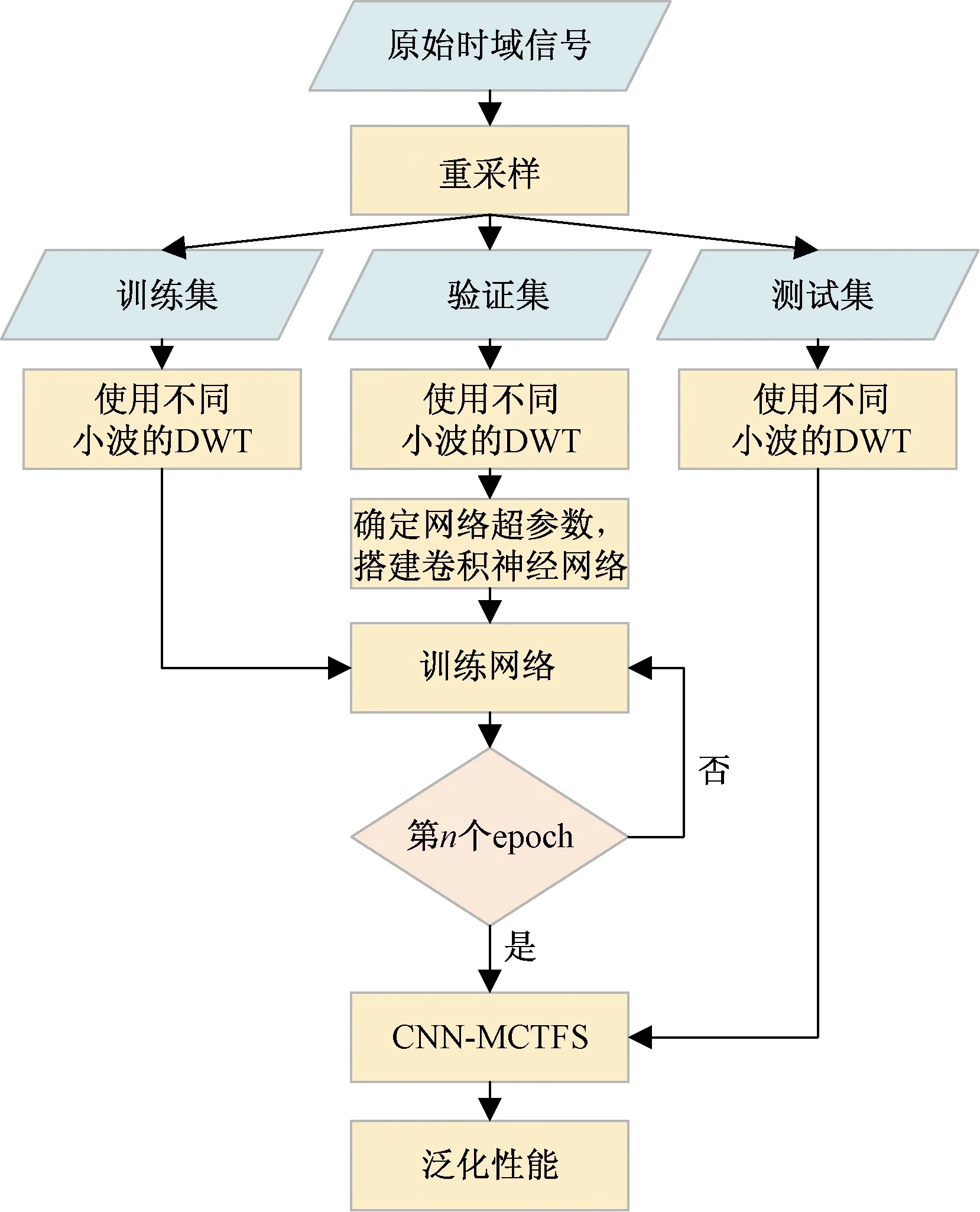
图5 滚动轴承智能故障诊断算法流程图Fig.5 Flow chart of intelligent fault diagnosis algorithm for rolling bearing
Step1重采样。从加速度传感器采集原始时域信号,通过重采样增加每一类的样本数量。
Step2构造多通道时频域信号。重构误差选取合适的小波,时域信号被多个不同的小波转换成时频域信号,从而组成多通道时频域信号。
Step3确定超参数。使用验证集确定网络的各个超参数,以搭建CNN。本文所用的损失函数为
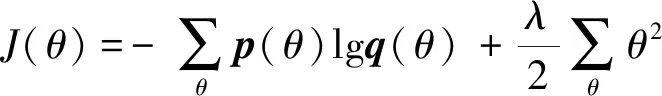
(7)
式(7)中:第一项是交叉熵损失函数;θ表示各个可学习参数;p(θ)表示标签的正确概率;q(θ)表示预测概率。第二项是L2正则化项,λ是正则项权重。使用Adam算法最小化损失函数,并不断更新可学习参数,表示为
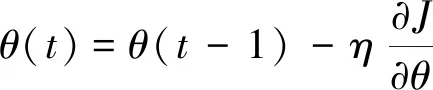
(8)
式(8)中:J表示损失函数值;η表示学习率;t表示第t次更新参数。
Step4训练网络。直至训练epoch次后,得到一个训练过的CNN-MCTFS。
Step5测试网络。用测试集测试CNN-MCTFS在变负载下的故障诊断能力。
4 实验方案及分析
4.1 数据集描述
所用到的滚动轴承时域振动信号公共数据来自凯斯西储大学(Case Western Reserve University,CWRU)轴承数据中心。采样频率为12 kHz,负载为1~3 hp,待采集振动信号的滚动轴承型号是SKF6205,用电火花在轴承的内圈(inner race,IR)、滚动体(ball)和外圈(outer race,OR)加工损伤直径分别为0.177 8、0.355 6、0.533 4 mm的单点损伤,再加上正常的类别,即共有10个类别,如表3所示。
从加速度传感器采集到的原始振动信号是一维时域信号,为了满足CNN对数据量的要求,采用重采样实现数据集扩容。本文的训练集制作过程,就是从各段信号第1个数据点开始,每移动32个数据点作为一个样本采集起始点,采集连续的256个数据点作为一个样本,这样既可以采集到每一类的大量数据,又可以充分学习到类别的特征,如图6所示。在负载1~3 hp下,每一类采集到2 100个样本,其中2 000个属于训练集,另外的100个属于验证集。而测试集不可与训练集重叠,所以在每一类别中,测试集需要在第2 100个样本的最后一个数据点之后采集,每256个点采集为一个测试集样本,从每个类别里各采集100个样本作为测试集,如表3所示。
4.2 实验环境及模型参数
实验环境是Ubuntu 16.04 LTS,Intel Core i7-67000 CPU@3.40 GHz,16 GB RAM,GeForce GTX 1080,CUDA 11.0,Python 3.6.9,PyTorch 0.4.1。根据上述滚动轴承智能故障诊断流程,在验证集上经过多次试验,得到本文所用算法超参数如表4所示。

表4 超参数
4.3 实验结果及分析
4.3.1 分解层数的选取
level不同得到的多通道时频域信号不同,对最终的分类结果也会造成不同的影响。最大分解层数由信号长度和小波长度共同决定,当信号长度分解到小于小波长度时,就达到了最大分解层数。在本文信号长度下,rbio2.2、bior2.2、coif1和db3小波的最大分解层数是5,因此level=1~5的分类精度如图7所示。从图7中可知,所有level的平均精度(average accuracy, AVG)均达到了0.950以上,由此证明该算法在任何level下都达到了较好的分类效果。但level=5的效果最好,AVG达到了0.975,相比其他level至少高出了0.012。这是由于level越大,输入到CNN的多通道时频域信号蕴含的多尺度信息越多,使得网络的分类精度就越高。因此,在接下来的实验中,均是对时域信号进行level=5的DWT。

图7 不同level的精度Fig.7 Different levels of accuracy
4.3.2 与其他算法的比较
在此实验中,将CNN-MCTFS与SVM(support vector machines)、MLP(multi-Layer perceptron)、文献[14]、WDCNN[15]和TICNN[8]进行对比实验,实验结果如图8所示。SVM的AVG只达到了0.614,也从侧面验证了传统智能故障诊断算法在变负载下的效果较差。当由MLP进行实验时,AVG明显提升了0.069,说明神经网络的拟合输入的效果强于SVM等传统机器学习算法。之后基于CNN的算法的AVG都达到了0.910以上,证明CNN的泛化性能较强。并且CNN-MCTFS的AVG达到了0.975,相比TICNN提高了0.043,相比WDCNN提高了0.010,因此该算法在变负载下可以有效识别滚动轴承的健康状态。

图8 不同算法之间的比较Fig.8 Comparison between different algorithms
而且,在CNN-MCTFS中,A-B的0.992要高于A-C的0.986,C-B的0.987要高于C-A的0.920,可以从中发现算法在相邻负载的效果要好于负载相差较大的,因此要尽可能收集多种负载下的数据,缩小训练集负载与测试集负载的差距。并且算法在中低负载下训练的效果要强于在高负载下的,例如A-C的0.986要高于C-A的0.920,B-C的0.996要高于C-B的0.987,因此也要尽可能地多收集中低负载下的信号作为训练集。
4.3.3 消融实验
将CNN-MCTFS与最原始的CNN(MaxPool, no-dilation)-T,将多通道时频域信号替换成时域信号、频域信号、单通道时频域信号的CNN-T、CNN-F、CNN-rbio2.2,将全局最大池化替换成最大池化的CNN(MaxPool)-MCTFS,将空洞卷积替换成3×1卷积的CNN(no-dilation)-MCTFS相比较,实验结果如图9所示。由于时域信号的特征不明显,时域信号在浅层网络中的AVG最高达到了0.916,而如果将时域信号变化到频域或时频域中,AVG则达到了0.948和0.939,而CNN-MCTFS的AVG相比它们至少多出了0.027,说明多个小波的共同使用可以挖掘出时域信号更丰富的特征,可以让CNN提取到更抽象的特征,从而提高分类精度。在将最大池化替换成全局最大池化,提取了每一Conv的最大激活后,CNN-MCTFS的AVG相比CNN(MaxPool)-MCTFS高出了0.024,而提高每一个Conv的卷积核的感受野之后,CNN-MCTFS的AVG相比CNN(no-dilation)-MCTFS提升了0.036。因此,CNN-MCTFS在变负载下取得了较高的诊断精度。
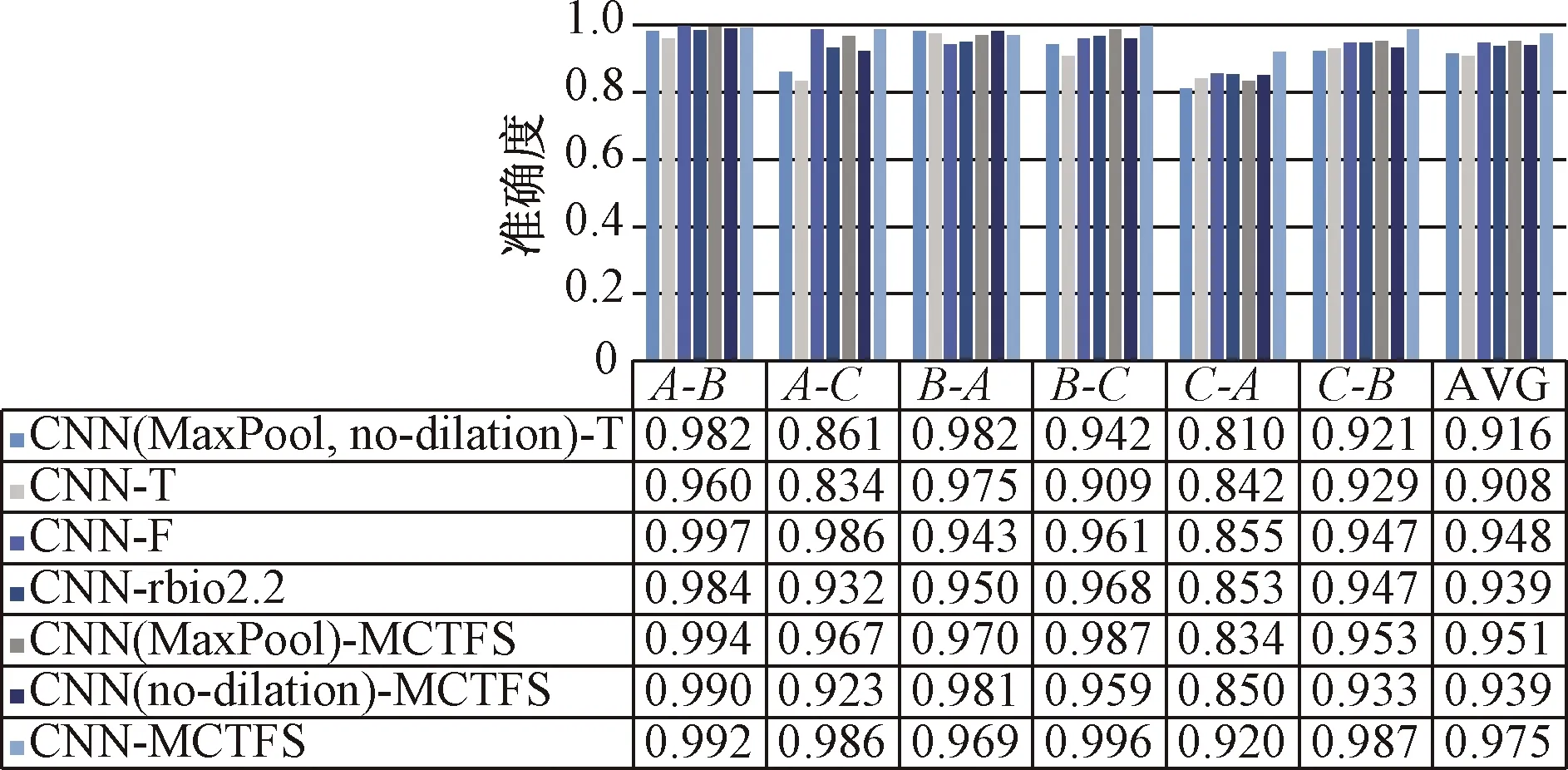
图9 各贡献点之间的比较Fig.9 Comparison between contributions
4.3.4 可视化各层特征
为进一步说明CNN-MCTFS的负载域适应能力,在C-A中,利用t-SNE(t-distributed stochastic neighbor embedding)算法[16]可视化数据集A在每一层的分布情况,如图10所示。在输入层中,所有样本聚成一簇。经过第1层Conv后,正常类样本逐渐聚集在一起,并与其他类样本分离,但每一类样本已经有了聚类的趋势。经过第2层Conv之后,正常类样本首先聚集在一起,并游离在外。经过第3、4层Conv之后,所有样本被分成10类,但还有少量样本散落在其他簇中。在分类层,基本上所有样本都被正确分类,但只有少数样本被错分。如图11所示,主要是IR0.355 6 mm被错分为OR0.355 6 mm和OR0.533 4 mm,ball0.533 4 mm被错分为ball0.177 8 mm,因此之后的研究要强化对这两类样本的正确分类。

图10 C-A中各层的特征分布Fig.10 In C-A, the feature distribution of each layer
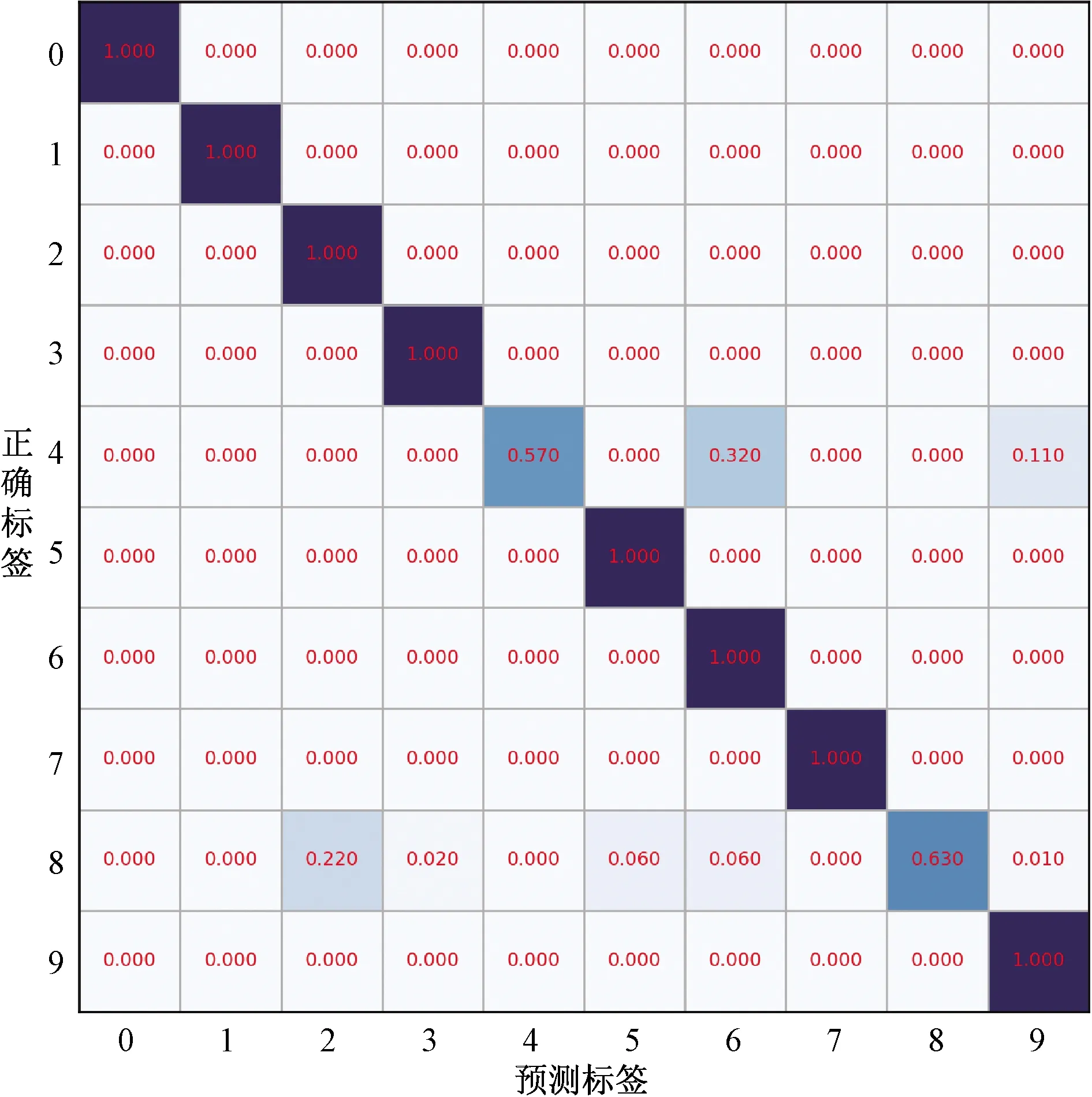
图11 混淆矩阵Fig.11 Confusion matrix
5 结论
在滚动轴承故障诊断中,为有效诊断滚动轴承在变负载下的健康状态,需要算法具有较强的负载域适应能力。提出了基于多通道时频域信号的卷积神经网络算法(CNN-MCTFS),得出如下结论。
(1)空洞卷积扩大了每一Conv的卷积核宽度,使得CNN在无需加深网络以及计算量的前提下,获得了较大的感受野。
(2)最大池化被替换成了全局最大池化,从全局范围内选取最大激活,从而最大程度地保留了许多重要特征。
(3)与时域信号、频域信号、单通道时频域信号相比,多个小波的共同使用为CNN提供了更丰富的特征。
(4)最终,CNN-MCTFS在变负载下的AVG达到了0.975。上述实验过程表明,在没有目标域数据的参与下,CNN-MCTFS也可以有效识别出滚动轴承的健康状态,相比于其他算法具有更强的负载域适应能力,在轴承类设备的故障诊断中具有广阔的应用前景。

