基于工程实例的非线性问题数值软件选取分析
赵亚鹏, 孔 亮
(1.青岛理工大学土木工程学院, 青岛 266033; 2.青岛理工大学理学院, 青岛 266033)
不同的工程材料往往具有不同的应力应变关系,或者说对应不同的强度准则[1-3],一般可将工程材料分为金属材料和非金属材料,金属材料的力学行为较为简单,如广泛采用的Tresca准则,认为金属材料表现为静水压力的非相关性[4],而在非金属材料中,典型代表则为岩土材料,主要表现为压硬性[5],或者称为静水压力相关性。岩土材料的应力应变关系较为复杂,现代土力学理论一般采用增量的弹塑性理论来解决岩土材料进入塑性阶段后的力学问题[6-8],而这种非弹性的弹塑性力学关系即为典型的非线性关系。工程材料的非线性力学问题如果按照普通的解析方法求解较为困难且不实际,在计算机发展早期,由于硬件的局限性,数值解法的应用并不突出,随着计算机的革命,计算机性能越来越高,数值解法的优越性逐渐凸显并被广泛应用,并随之出现了一系列的基于不同算法的数值模拟软件[9]。根据不同研究角度,广大学者开展了一系列的数值模拟研究工作,并取得了大量研究成果,但是针对非线性问题的数值模拟软件选取及其建模过程的分析相对较少,而模拟软件的选取及建模又对分析结果有着重要影响,因此有必要对模拟软件选取的相关内容作进一步分析。首先对数值模拟进行概括性分类总结及介绍,并对其发展趋势进行简要分析,在此基础上结合具体工程(采矿领域)实例就非线性问题的数值软件选取相关内容展开讨论,可为相似地质条件下的非线性问题数值软件选取及建模提供参考。
1 数值模拟分类
依据不同的划分原则,可将数值模拟划分为不同类别,例如:根据求解微分方程方法的不同,可以划分为有限元法、有限差分法、边界元法、有限体积法等[10];根据研究对象的连续与否,则可划分为连续介质分析方法与非连续介质方法[11]。
1.1 有限单元法
有限单元法(finite element method ,FEM)以变分原理和加权余量法为基础,其基本原理是将连续的研究对象离散成有限个单元,各单元之间由有限个节点相联系[12],即将一系列的微分方程离散化,再编制相应的计算机程序,借助计算机进行求解。而根据更为具体的分析方法,有限元法又可分为里兹法、伽辽金法等[13]。随着计算方法的不断发展,一种有别于传统有限单元法,而基于广义有限单元法的多尺度单元法被提出[14],由于该方法的基函数具有多尺度特性,因而被广泛应用于解决多孔介质渗流问题[15]。目前基于有限单元法的数值软件众多,且多用于解决固体力学及结构力学问题,常用的模拟软件有ANSYS、ABAQUS、COMSOL等。有限单元法从本质上来说属于连续介质分析方法。
1.2 离散单元法
离散单元法(discrete element method ,DEM)在求解方式上属于显示求解方法,其与有限单元法类似,都是将连续的研究对象划分成有限个单元,但是各单元之间的节点可以分离,这与有限法元截然不同。单元之间的作用力则由力与位移的关系求出,个别单元的运动规律可由牛顿第二定律得出[16]。由于离散单元法所划分单元之间的离散特性,该方法可以对二维及三维空间内的连续对象进行离散颗粒之间的力学行为研究,而当颗粒的尺寸足够小时,则可反映研究对象的微观属性,因此离散元法又被认为是宏微观研究相结合的有效桥梁[17]。离散单元法在非连续介质领域如散体力学、断裂力学、爆炸力学方面得到了广泛应用[18-19],此外也被广泛应用于结构工程、岩土工程等领域[20]。离散单元法数值软件的典型代表为颗粒流程序(particle flow code ,PFC),此外还包括UDEC(universal distinct element code)、3DEC(3 dimension distinct element code)等。离散单元法属于非连续介质分析方法。
1.3 有限体积法
有限体积法(finite volume method ,FVM)首先将研究区域划分为有限个体积,然后再进行方程式的构建,区别于有限单元法和离散单元法,有限体积法基于积分形式的守恒方程而不是微分方程。该方法从物理观点来构造离散方程[21],每一个离散方程都是有限大小体积上某种物理量守恒的表示式,物理意义明确。有限体积法被广泛应用于流体力学研究领域[22-23]以及用以解决传热传质学等问题[24]。有限体积法的常用数值软件有FLUENT、FLOTHERM、STAR-CD等。
1.4 边界单元法
边界单元法(boundary element method ,BEM)是在有限元法之后衍生并发展起来的一种数值方法,其主要特点在于仅在连续介质的边界上划分单元,用满足控制方程的函数去逐渐逼近边界条件[25],这与有限元在连续介质内划分单元有着很大区别。正是由于边界元法的特殊性,使得对于某些特殊的研究对象,可以达到化整为零、维度降低的效果,在保持较高精度的同时大幅简化计算过程[26]。边界单元法在断裂力学、运动边界尤其是解决无限与半无限问题方面具有十分广泛的应用[27-28]。与其他方法相比,目前专门的边界元软件相对较少,有LINFLOW等。该方法也属于连续介质分析方法。
1.5 有限差分法
有限差分法(finite difference method,FDM)首先对连续介质的研究对象进行网格划分,然后基于所划分的网格点,以差商代替微商[29],本质是将研究问题离散为差分格式进而求解,其又可具体分为显示差分与隐式差分。有限差分法具有广泛的适用性,易于编程且容易利用计算机实现,但是对研究区域的连续性要求较高。在传统有限差分法基础上,近期又发展出一种无网格形式的广义有限差分法[30-31],进一步扩展了有限差分的适用性。有限差分法的典型模拟软件为FLAC3D,其被广泛应用于岩土工程、地下工程及采矿工程[32-33],尤其适用于解决大变形问题。
2 数值模拟发展趋势
从20世纪50年代数值模拟技术诞生起,其发展历程就与计算机技术紧密联系在一起,计算机技术与数学等多学科的交叉融合则共同促进了数值模拟领域的快速发展,相应地,数值模拟又对各研究领域起到了反哺促进的作用。经过数十年的发展,数值模拟方法已经成为各个研究领域较为成熟的常规分析方法,通过对大量数值模拟研究成果的总结,可以认为当前数值模拟研究有着如下的三大发展趋势。
2.1 多相及多物理场耦合
数值模拟在诞生初期受限于计算机硬件以及算法的不足,仅能对低维、低相以及单一物理场进行模拟,其研究成果也仅能作为特定前提条件下的结论参考。随着计算机发展以及各种算法的提出,同时基于工程实际的需求,实现三维状态下的多相及多物理场耦合影响研究成为广大学者们的一致诉求。目前对于多相及多物理场模拟研究已经取得了一定成果,如应力-渗流耦合研究[34]、温度-应力耦合研究[35]、温度-应力-渗流-化学耦合研究等[36]。
2.2 计算方法耦合
根据前述可知,数值模拟方法可以分为有限元、离散元、边界元及有限差分等不同类别,而各种方法都有其自身优缺点,即不同方法具有不同的适用性。经过长期的研究工作,发现某些研究对象往往具有多重属性,或者同一研究对象在不同区域具有特定特性,又或者研究对象本身是由两种不同属性结构组合而成(如对含断层地层进行分析时,断层及完整岩层则具有不同属性),此时如果将计算方法相耦合则可以在集不同方法优点的同时弥补单一方法的不足。较为常见的耦合计算方法如有限元与离散元耦合[37]、有限差分与离散元耦合[38]、边界元与离散元耦合等[39]。
2.3 二次开发数值模拟
数值模拟作为一种研究方法,其最终目的仍然是指导工程实践,这与实验研究、理论分析等研究方法相一致。而不同研究方法之间以及研究结论与工程实践之间往往会有一定出入,正如前述分析,无论是多物理场耦合还是计算方法耦合,都是为使研究结果更贴近于工程实际。然而大量研究结果表明,对于某些特殊环境中的研究对象,采取常规方式并不能得出理想结果,此时对数值模拟所依赖的本构模型等进行改造显然是一种更深层面的解决办法。例如考虑非共轴影响的二次开发数值模拟[40]、基于FLAC3D黏土边界面模型的隧道施工分析[41]、基于ABAQUS平台的纤维弹塑性本构模型开发等[42]。
3 实例分析
3.1 工程概况
研究区域包含3上及3下两层可采煤层,煤厚分别为5 m和4 m,煤层间距4 m,煤层倾角1°~7°,平均4°,属半亮-半暗型气煤,色黑、性脆,似玻璃光泽,硬度2.2~2.5。区域内对工作面影响较大断层主要有田岗断层和二龙岗断层,田岗断层走向169°~186°,倾向79°~96°,倾角∠70°~75°,落差H为300~410 m,属台阶状断层;二龙岗断层走向180°~188°,倾向270°~278°,倾角∠65°,落差40~83 m,两断层均属不导水正断层。距离3煤底板26 m为三灰含水层,平均厚度7 m,水压最大2.9 MPa。工作面布置分别为23上614及23下614工作面。工作面及断层位置关系见图1。
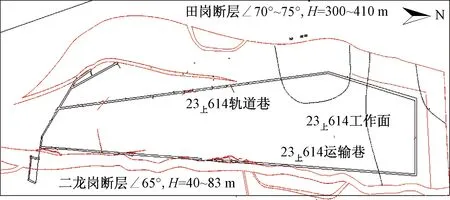
图1 工作面平面图Fig.1 Plan of working face
3.2 研究内容
基于地质概况,并结合工程实际,主要研究内容如下。
(1)研究在近距离煤层下行式开采过程中的覆岩运动规律。
(2)针对三灰含水层,研究底板承压水对回采过程的影响规律。
(3)对工作面开采过程中,断层的活化规律进行研究,尤其是田岗台阶状断层的活化规律。
(4)研究确定田岗及二龙岗断层的合理煤柱尺寸。
3.3 软件选取
数值模拟软件的选取需要考虑诸多因素,基于以上工程概况,主要考虑如下角度。
3.3.1 实际工程地质概况
数值软件的选取最根本的出发点,应是以实际地质概况为基础。本工程需要考虑的因素主要有:
(1)田岗断层与二龙岗断层。即在数值模拟时,需要考虑断层的存在,这就需要模拟软件能够解决断层与周围岩层的接触问题[43]。
(2)三灰含水层。由于承压水的存在,在进行普通应力场分析时,还需要考虑渗流场的问题,即数值模拟软件必须能够进行流固耦合的多场分析。
3.3.2 研究内容及目的
在正式进行一项研究工作之前,首先应确定研究目的及研究内容,此后的研究工作也应以此为依据而具体展开。不同的研究内容及目的,一般所采用的研究手段也不尽相同,因此就试验与模拟的研究手段来说,无论是试验设备还是模拟软件都应根据具体的研究内容及目的进行具体化的选择。针对本工程,试验与数值模拟部分在考虑前述研究内容与目的基础上将具体结合其他考虑因素进行综合确定。
3.3.3 与其他研究方法相对应
这一因素主要是基于研究方法“整体性”的考虑。本工程除了采用数值模拟的研究手段外,还采用了“相似材料模拟试验”的研究方法。图2所示为相似材料模拟试验设计图及铺设完成图。
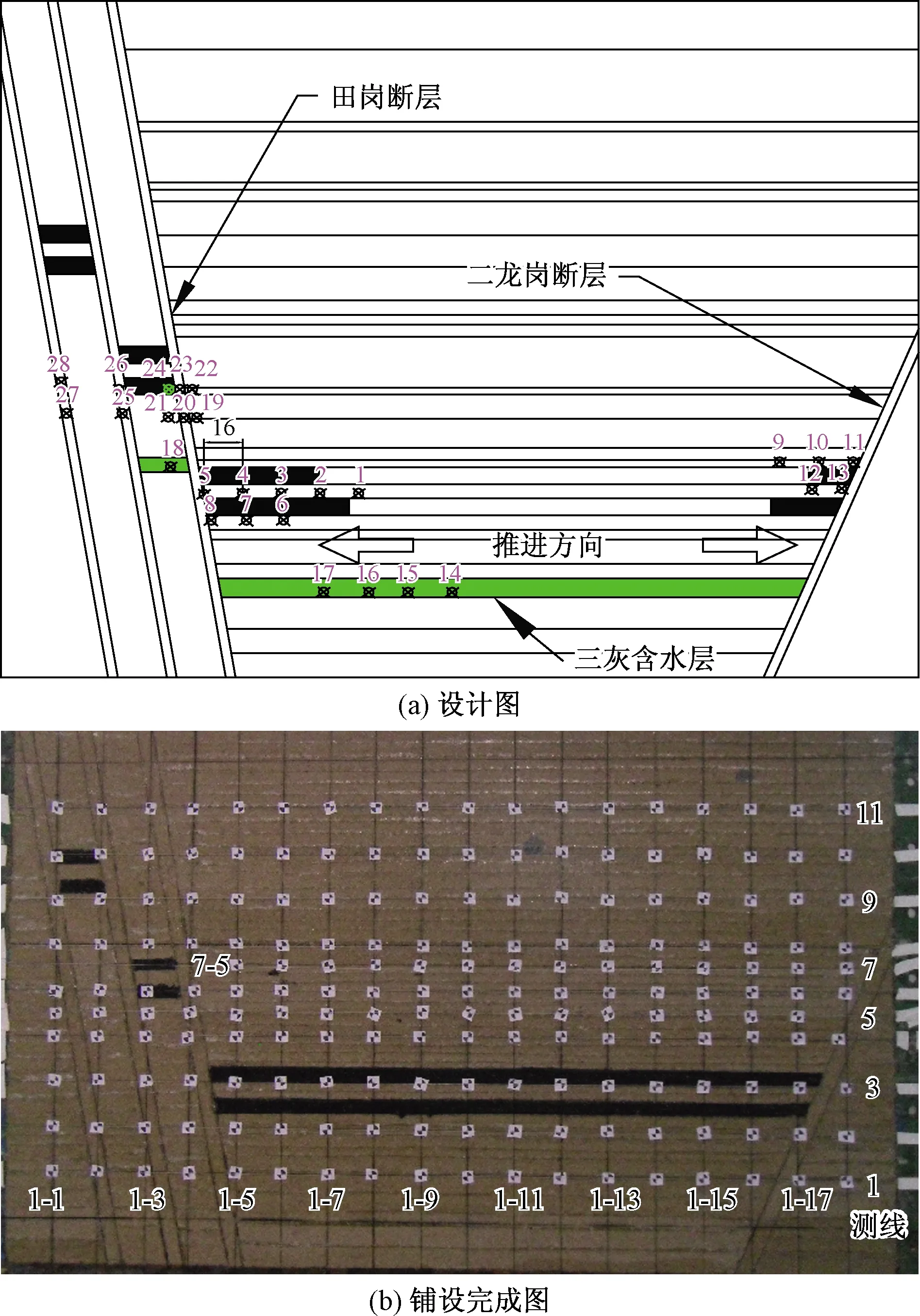
图2 相似材料模拟试验图Fig.2 Diagram of similar material simulation experiment
基于研究手段之间的“呼应”关系,数值模拟部分应该将“相似材料模拟试验”内容作为软件选取及建模时的考虑因素。就此试验部分而言,数值模拟部分的模型规模应与试验对应,即至少要包括“台阶田岗断层”、二龙岗断层、三灰含水层以及上覆和下伏岩层,此外,其所选软件的模拟结果应尽可能与试验结果相对应。
3.3.4 研究对象及行业领域
主要是指整体性的研究领域。就本工程而言,其首先属于采矿工程领域、其次可将其扩展为岩土工程及地下工程领域。基于此,首先在领域范围上,对于数值模拟软件的选取就已经有了一定的倾向性(更为具体的软件选取考虑角度将在后续内容中提到),如岩土工程领域常用的FLAC3D、ANSYS、PFC、ABAQUS等[44-46]。
3.3.5 其他因素
在此将以上四类之外的考虑因素以及更为具体化的考虑因素统称为其他因素,主要包括:
(1)本构模型。不同的研究对象其应力应变关系不同,因而选取的本构模型也不同,最为代表性的就是金属材料和岩土材料。本工程涉及的煤层开挖问题,属于岩土的本构关系,一般岩土的本构关系,莫尔库伦准则相对比较准确[47-48]。因此考虑含有莫尔库伦模型的模拟软件。
(2)开挖问题。本工程主要研究煤层开挖问题,因此,模拟软件必须能够对岩体开挖进行模拟,模拟开挖问题的软件也较多,如FLAC3D、ANSYS、PLAXIS等[49-51]。
(3)大变形问题。大型滑坡问题以及本工程所涉及的煤层开挖问题一般都属于大变形问题,如本工程涉及两层煤层8 m岩层的开挖,其在走向长度上工作面的长度可达数百米,因此可以想象本工程的数值模拟必然面临大变形的问题。与有限元主要解决小变形问题不同,在大变形及大面积屈服方面,FLAC3D具有明显的优势[52]。
(4)模型规模。模型规模包含模型尺寸、网格多少、节点数量等内容。本工程针对的对象较为复杂,包括多条断层,此外水平岩层多达20余层,而针对断层活化,断层带需要进行网格的细化,此外还要考虑竖向断层与水平岩层的对接问题,可想而知,整个模型的节点及网格数量庞大,其最终导致计算过程也必然较长。FLAC3D采用的拉格朗日算法在计算中不形成刚度矩阵,不需迭代满足弹塑性本构关系,而只需通过应变来计算应力。因此对于大体积、划分单元及结点数较多的非线性岩体的开挖计算来说是较适宜的[53]。
(5)建模问题。前面已经分析,本次模拟所需建立的模型规模较大,前期建模过程也将相对复杂,在建模方面,ANSYS优势明显,而FLAC3D在建模方面较为“呆板”,但是针对FLAC3D建模方面的短板,可借助“RHINO”软件强大的建模能力,其可对包括FLAC3D、ANSYS在内的多款模拟软件进行模型文件输出[54-55]。
(6)覆岩垮落问题。本工程中的一个研究角度就是对近距离煤层开采时的覆岩垮落规律进行研究,此内容在试验部分已经进行了研究,因此考虑数值模拟中也可对此内容进行部分体现。由于FLAC3D采用显式算法获得模型全部运动方程(包括内变量)的时间步长解,从而可以追踪材料的渐近破坏和垮落[56-57],这与本次研究内容相对应。
3.4 建模思路(过程)
基于以上分析,本工程采用FLAC3D作为所选取的模拟软件,建模的思路(过程)如下。
3.4.1 地质岩层汇总
首先对地质岩层类别进行汇总与归纳,主要以实际地质钻孔所获得的钻孔柱状图为依据,获得模拟范围内的各岩层厚度及岩层分类。
3.4.2 确定模型尺寸
模型高度及宽度尺寸的确定主要以“研究角度范围”(如本工程研究覆岩垮落,则需要考虑对纵向高度的覆岩垮落范围进行预留)、“研究对象范围”(如本工程涉及的两断层、含水层)、“边界范围(要考虑模型的边界效应)”及“其他因素”(如与试验研究相对应)为侧重点。
3.4.3 模型建立
可采用“RHINO”软件对模型进行建立,主要针对复杂模型,如本工程的模型或模型表面有起伏等复杂模型,建立完成后输出为FLAC3D文件;也可采用ANSYS软件进行建模,其与FLAC3D可进行对接;或者对于相对简单的模型采用CAD进行模型的“粗建”,获得所需各点坐标后,再根据坐标在FLAC3D中进行建模,此方法虽然较为烦琐,但是网格划分效果较好,对于本工程中断层带的网格细化较为有利;对于更为简单的模型,当然应直接在FLAC3D中进行模型建立。
本工程综合考虑,最终采用了首先在CAD中进行“粗建”,获得坐标后再进行FLAC3D软件建模的方法,各点坐标在EXCEL表格中采用公式计算,并将FLAC3D的建模命令也转移至EXCEL文件中进行,最终将所有命令导出为“TXT”文件,供FLAC3D直接读取。其整体的建模过程也并不十分复杂,可供参考。所建模型尺寸为:长×宽×高=500 m×200 m×220 m,模型节点、网格数量分别为317 460和299 750,最终建立完成的模型如图3所示。
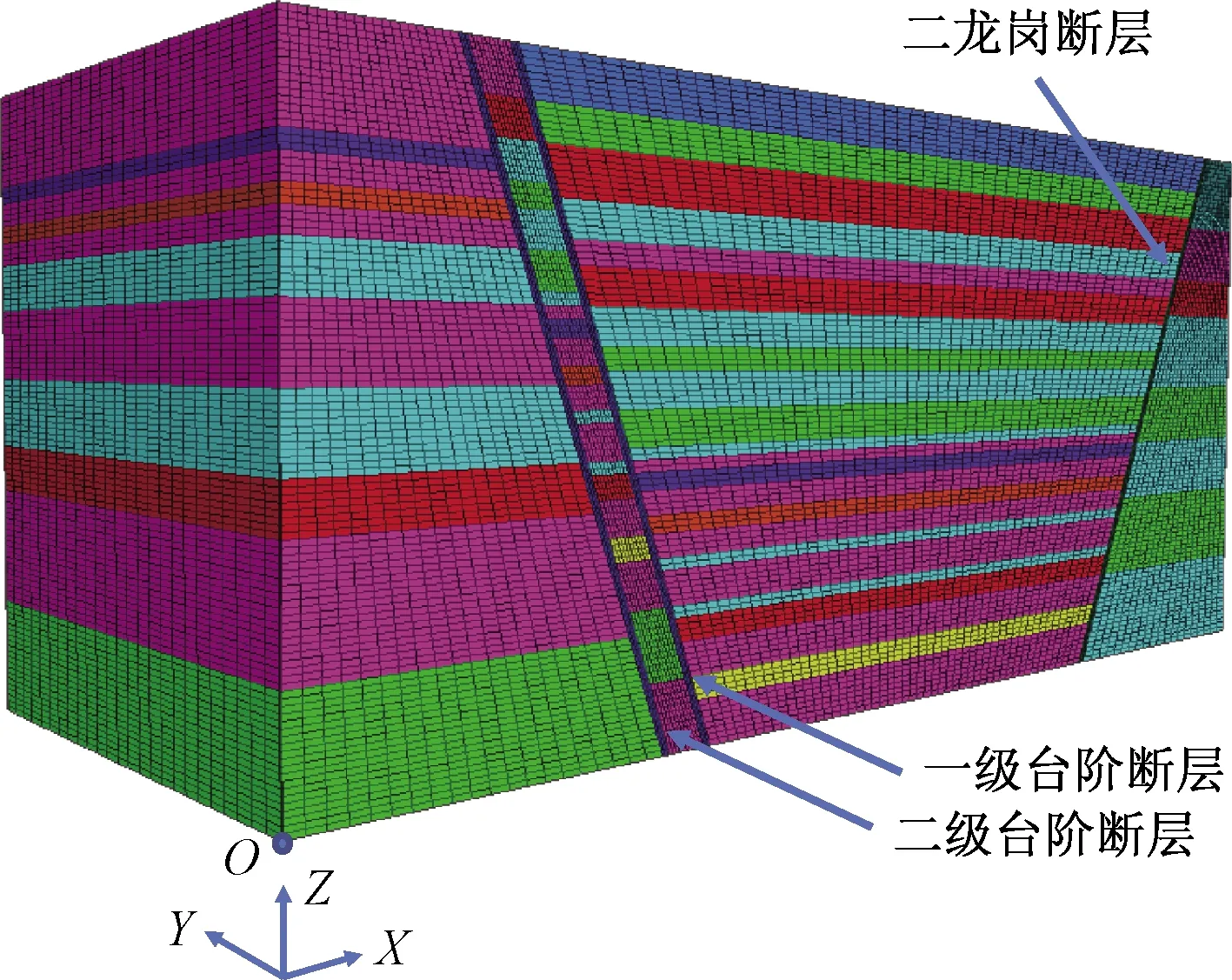
图3 模型网格划分及断层示意图Fig.3 Model meshing and fault division
3.5 测点设计
模拟软件的模拟过程通常主要研究应力场,其次还涉及渗流场、温度场等多场的耦合[58-59],而具体来说则主要有应力、位移、塑性区、水压等各种模型数据。除了整体的模型云图外,常规监测方式还包括测点以及测线的布设,对分析过程中的以上数据进行监测,而这些测点与测线的设置应当遵循一定的原则。
(1)以研究内容、对象及研究目的为设置依据。
(2)选定的测点及测线位置应当具有一定的区域代表性或宏观代表性。即所获得的数据规律应具有一定区域或类似工程概况的普适性。
(3)避免重复设置。应当避免对类似测点的重复性设置,一方面,重复设置获取的数据规律具有重复性、类似性;另一方面,会增加计算及后处理的工作量。在具有代表性的基础上,重复性设置显然也是没有必要的。
(4)差异性设置。即当研究角度、侧重点不同时,即使是相同或类似的研究对象,也应避免“一概而论”性设定。
本次模拟在整体云图分析的基础上,也布设了大量的应力、位移、水压测点和测线。通过对本次模型云图及测点的分析,其呈现极强的规律性,并与文献[60-61]结论一致,这也说明本次模拟过程较为成功。本次模型布设的相关测点及测线主要有:两级台阶断层带应力、水压测线、煤层底板不同深度(10、20、50 m)应力、位移测线、煤层间位移测线等。
应当进一步说明的是:针对断层带应力测点,在一级台阶断层及二级台阶断层的断层界面处沿煤层顶、底板每隔10 m布设一应力测点,其中顶板测点距离煤层(3上煤)的高度设定为正值,底板测点距离煤层的深度设为负值;各坐标方向如图3所示。提取相关数据后整理的数据曲线如图4~图6所示。
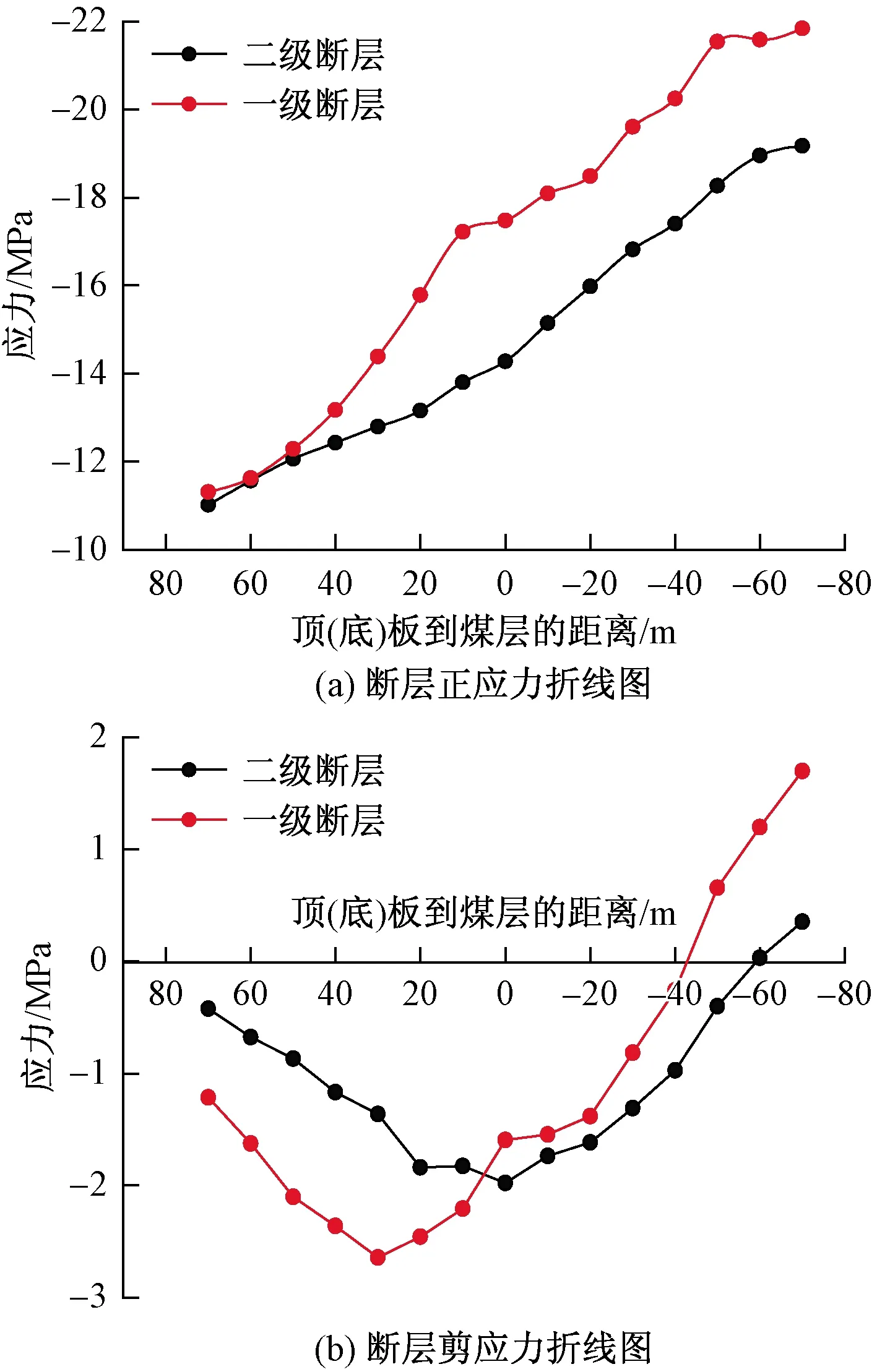
图4 3上煤煤柱尺寸为80 m时,两级断层界面应力变化Fig.4 The stress change law of two-stage fault interface when the pillar size of 3upper coal is 80 m
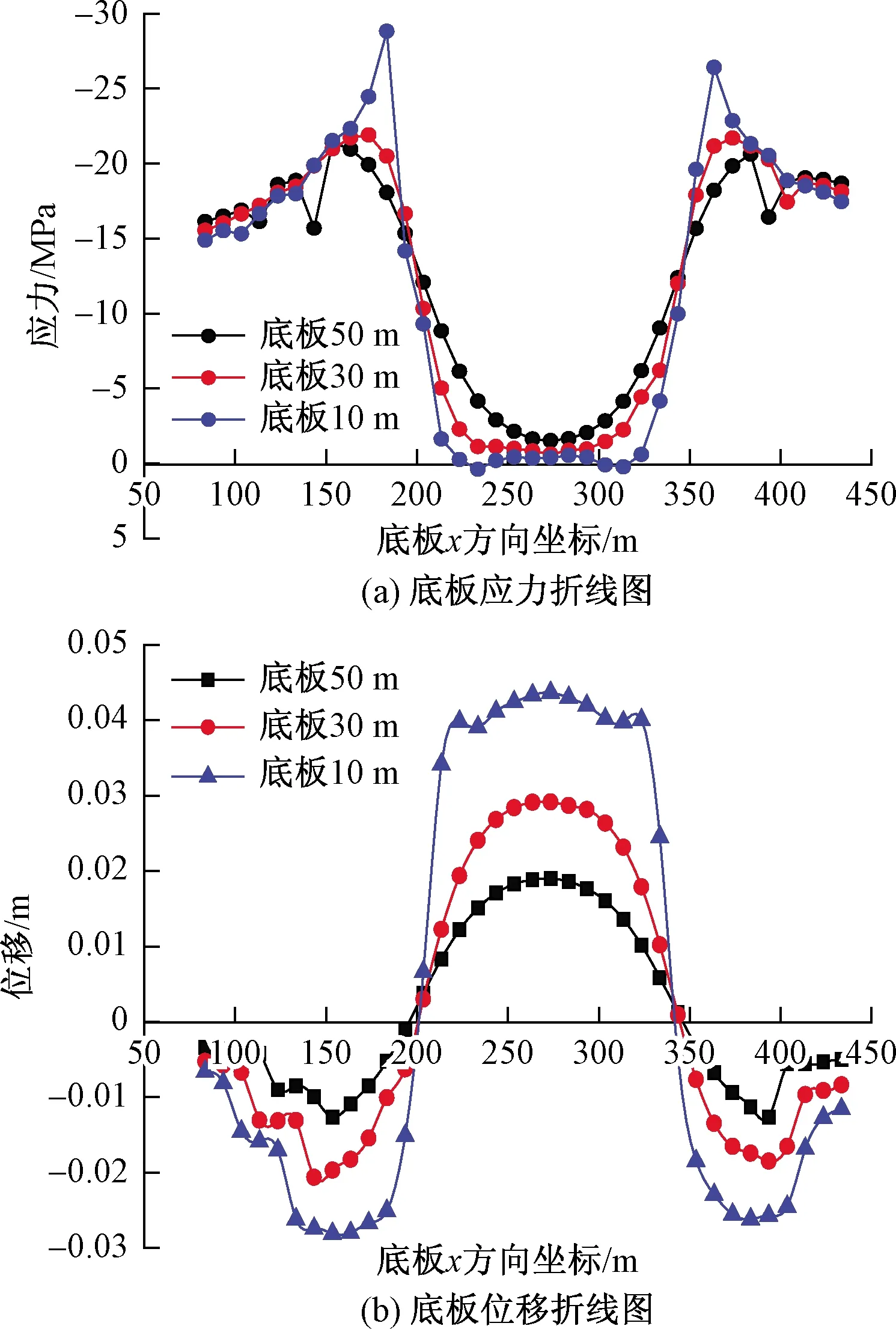
图5 3上煤煤柱尺寸为80 m时,底板应力位移图Fig.5 The change law of stress and displacement of floor when the pillar size of 3upper coal is 80 m
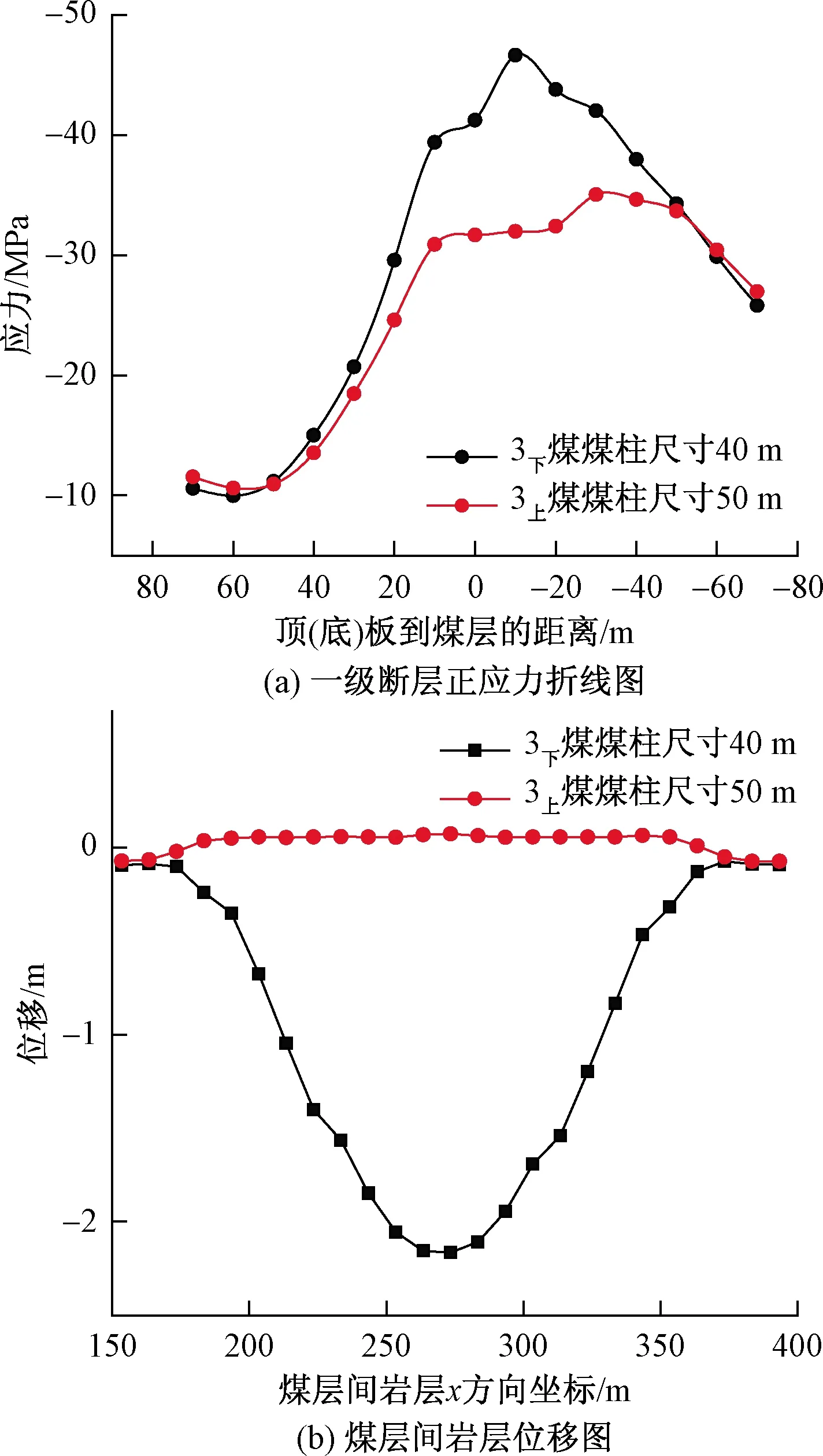
图6 3上、3下煤开采对比Fig.6 Comparison of 3upper coal and 3lower coal
根据以上绘制的应力、位移、水压变化曲线,可知,数据呈现极强的变化规律,且符合煤层开挖过程中的应力、位移变化规律,这说明无论是软件选取、模型建立还是开挖过程模拟,都是比较合理的,这也进一步印证了前文所述内容的相对合理性。
4 结论
数值模拟与试验研究相结合的方式已经成为各个研究领域常规的研究构架,不同研究方法之间的结果印证也使得宏观结果更具说服力。正是在这一思路下结合具体工程实例就试验研究基础上模拟研究的一般考虑因素或构思过程展开讨论,文中所述内容具有一定的宏观代表性,同时又具有特定案例专属性,可为相似工程案例数值模拟软件选取及建模提供参考。主要结论如下:
(1)数值模拟的发展趋势为:多相及多物理场耦合、计算方法耦合以及二次开发数值模拟。
(2)数值模拟软件选取时考虑因素主要有:实际工程地质概况、研究内容及目的、与其他研究手段相对应、研究对象及行业领域、其他因素(具体因素)。
(3)建模思路或过程为(结合本工程):地质岩层汇总、模型尺寸确定、模型建立(不同方法建模)。
(4)测点与测线的设置应当遵循的原则为:以研究内容、对象及目的为依据、具有一定的区域代表性或宏观代表性、避免重复设置、差异性设置。
(5)数据曲线呈现出极强的规律性,并与相关文献结论一致,印证了文中软件选取、模型建立、开挖过程以及测点布设的正确及合理性。

