基于高斯混合模型的敞开式质谱重叠峰解析方法
黄安贻, 缪东升, 闻路红, 郭 荣, 胡舜迪, 洪欢欢, 吴 帅
(1.武汉理工大学机电工程学院, 武汉 430070; 2.宁波大学高等技术研究院, 宁波 315211)
敞开式质谱是一种无需或仅需简单样品前处理过程,可在敞开环境下直接对样品实现离子化并进行分析的新型质谱技术,该技术能满足实时、快速的分析需求,同时兼具传统质谱分析高灵敏度、高通量等特点。敞开式质谱在开放环境工作时分子离子反应较复杂[1]、易受环境因素或复杂进样中其他碎片离子的影响[2],由于仪器分辨率较低,在质谱图中常出现重叠峰现象,为了快速、准确识别待测物特征峰,解析敞开式质谱重叠峰非常必要。
在质谱图的重叠峰解析中,常采用色谱和质谱联用技术或者高分辨率仪器来完成,而通过信号处理技术来解析敞开式质谱重叠峰的方法则有限[3]。解析重叠峰的方法主要有两大类[4]:一类是利用数学变换的方式对原始信号进行处理来分离重叠峰,如傅里叶自去卷积,小波变换等。傅里叶自去卷积技术中合适的去卷积函数和截至函数不仅能有效抑制负旁瓣效应的产生,同时能提高解析后的信噪比和分辨率[5],此外,还能较好地解析近乎完全重叠信号,但是该方法在重叠峰不对称时构建去卷积函数困难而解析效果较差[4];基于小波变换的重叠峰分析方法突破傅里叶分析时频单一的局限,充分利用基函数的时频局部特性在分离信号中噪声和有用信息的同时有效提高了解析后的分辨率[6-8],而且还能完成不同重叠程度的信号解析,但是与原始峰形相比解析后的峰强有所增大、峰宽变窄[3],从而影响提取离子流(extracted ion chromatogram,EIC)及检出限的设定。另一类是建立重叠子峰的数学模型,通过估计各子峰最优参数来实现分离,如曲线拟合等。曲线拟合技术基于最小二乘法原理使合成信号与实测重叠信号的误差平方和达到最小,实现彻底分离重叠峰的同时可获取各子峰的峰形特征,但是噪声干扰容易导致含糊的解析结果或者无法得到收敛的解[9-10]。
作为传统的质谱检测方法之一,EIC表示一定宽度内所有信号强度之和,常用来计算信噪比。EIC对谱峰的峰强和峰宽等峰形特征十分敏感,为了提高质谱检测的准确性和信噪比,基于高斯分布函数是描述质谱峰常用函数之一[11],以及高斯混合模型(gaussian mixture model, GMM)可逼近源信号的概率密度函数[12-13]、受谱峰重叠程度影响较小等优点,提出基于GMM的敞开式质谱重叠峰的解析方法,改变重叠峰的幅值比、分离度和噪声后进行解析,结果未改变峰形特征,并提高了信噪比。
1 高斯混合模型解析重叠峰理论
质谱峰形常用高斯分布函数来描述,故将原始重叠峰信号归一化为概率密度函数之后可用GMM模型来逼近,即构建重叠峰信号高斯混合的参数化模型,然后通过期望最大(expectation maximization, EM)算法估计模型中各高斯分布的参数[14-15],从而完成重叠峰的解析。采用GMM解析重叠峰流程如图1所示。
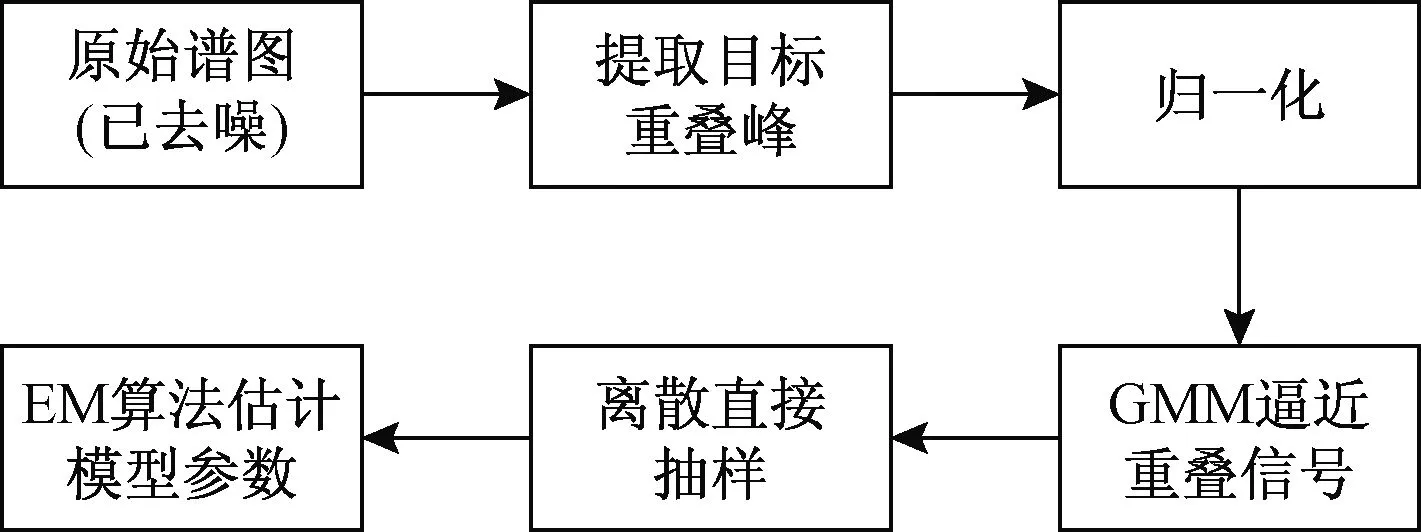
图1 重叠峰解析流程Fig.1 Flow of overlapping peaks analysis
GMM解析重叠峰的具体描述如下。
(1)将测量所得敞开式质谱数据作基线校正扣除背景噪声,获得较为干净的谱图。
(2)在目标质荷比(mass-to-charge ratio,m/z)位置提取重叠峰信号,将信号强度值归一化作为概率密度函数,构建高斯混合模型,然后由离散直接抽样按照该概率密度函数产生相应的随机数。
(3)采用EM算法对随机数进行迭代运算,求出GMM模型的各个参数,即完成重叠峰的解析。
在该方法中,需要解决的关键问题是EM算法估计模型参数时初始值的设置,包括簇数、每一簇的均值、标准偏差和权重。有效选取初始值可以缩小EM算法的搜索空间、避免算法的局部收敛[12, 16],使迭代计算更为高效准确。
1.1 GMM模型
GMM是一种基于统计学的聚类模型,其基本假设为数据是由几组不同高斯分布的随机变量组合而成,它能准确地逼近任意形状的密度分布[17-18]。若有数据集X是来自多个高斯分布的混合体,则其概率分布模型为
(1)
式(1)中:αi为各高斯分布的权重,αi≥ 0且各高斯分布的权重和为1;θi= (μi,σi2)为均值μi、方差σi2的向量表示;k为模型中符合高斯分布的分支个数;pi(X,θi)为概率密度函数,表达式为
(2)
1.2 离散直接抽样
直接抽样方法是对任意给定的分布函数,产生其样本的一种抽样方法。若有离散分布的变量x1,x2, …,xn(即质谱图中的质荷比),已知对应概率p1,p2, …,pn(即信号强度值归一化的结果),可计算出该组变量的累积分布函数为
(3)
式(3)中:p0=0, ∑pi=1。抽样时直接产生服从[0,1]均匀分布的随机数μ,求满足表达式的k值,即
F(Xk-1)<μ≤F(Xk)
(4)
离散变量的第k个值xk即为欲抽取的值。
1.3 EM算法估计模型参数
EM算法是一种求解似然估计的迭代最优化算法[19],通常用来估计GMM中各个高斯函数的参数。EM算法是当数据存在缺失问题时,在模型中引入隐变量之后再计算似然函数,交替迭代至对数似然函数收敛时停止,即可求解出各高斯分布的参数。
EM算法估计模型参数的具体步骤如下:
(1)变量初始化,需要初始化的参数有簇数k、每一簇的均值μ和方差σ2,以及隐变量W。在k、μ和σ2初值设定较为合理的情况下,对隐变量初值的要求大幅度降低,一般Wi,j设为1/k;而第j簇的权重根据隐变量求得,即
(5)
则权重初始值αj= 1/k。
(2)E步骤(期望):根据均值、方差和权重参数的初始值或者上一次迭代的估计值来更新隐变量(其中第i个变量属于第j簇的概率),即
(6)
再根据式(5)可更新每一簇的权重αj。
(3)M步骤(最大化):针对对数似然函数的期望值进行极大化估计,根据E步骤得到的隐变量值来更新均值和方差,第j簇的均值为
(7)
第j簇的方差为
(8)
(4)E步骤和M步骤交替迭代,直至收敛,即完成GMM的参数估计。
2 实验研究
2.1 仪器和试剂
Craiv-110质谱仪:宁波市华仪宁创智能科技有限公司;试剂:冰毒样品,浓度100 μg/L。
2.2 质谱条件
离子化能量70 eV;扫描速度4 000 amu/s;质量范围50~700 amu(1 amu为碳12原子质量的1/12);线性离子阱质量分析器;分辨率:半峰全宽,亦称半峰宽(full width at half mzxima,FWHM)为0.5;使用Python 3.7 编写程序进行实验。
2.3 GMM解析重叠峰
采用GMM解析重叠峰需要解决的关键问题:模型初始值的设置,包括簇数、每一簇的均值和标准偏差。对于实测数据,选取目标质谱峰信号附近存在干扰峰的重叠峰数据,本文选取冰毒碎片离子(m/z=119)的质谱峰进行重叠峰的解析实验。目标峰的峰形一般均可用高斯分布函数描述,则实验中采用多个高斯函数来模拟构建不同重叠形式的信号,从而验证GMM解析重叠峰的可行性、局限性以及抗噪声能力。
2.3.1 簇数的确定
在GMM模型中,簇数k需提前确定。本文采用手肘法从数据本身出发来确定簇数k。手肘法的核心指标是误差平方和(sum of the squared errors,SSE),定义为
(9)
式(9)中:Ci是第i簇;p是Ci中的元素点;mi是第i簇的均值。随着簇数k的增大,每个簇的聚合程度会逐渐提高,则SSE会逐渐变小。当k小于真实簇数时,由于k的增大会大幅增加每个簇的聚合程度,则SSE的下降幅度会较大;而当k到达真实簇数后,再增加k所得到的聚合度变化幅度会变小,即SSE的下降幅度会骤减直至趋于平缓,也就是说SSE和k的关系图是一个手肘的形状,称为手肘图,而这个肘部对应的k就是数据的真实聚类数。
通过上述手肘法确定重叠信号中的真实簇数k,结果如图 2所示。选择多种不同重叠情况的质谱信号,手肘图中肘部对应的位置平均簇数k=2处,故模拟重叠峰数定为2。
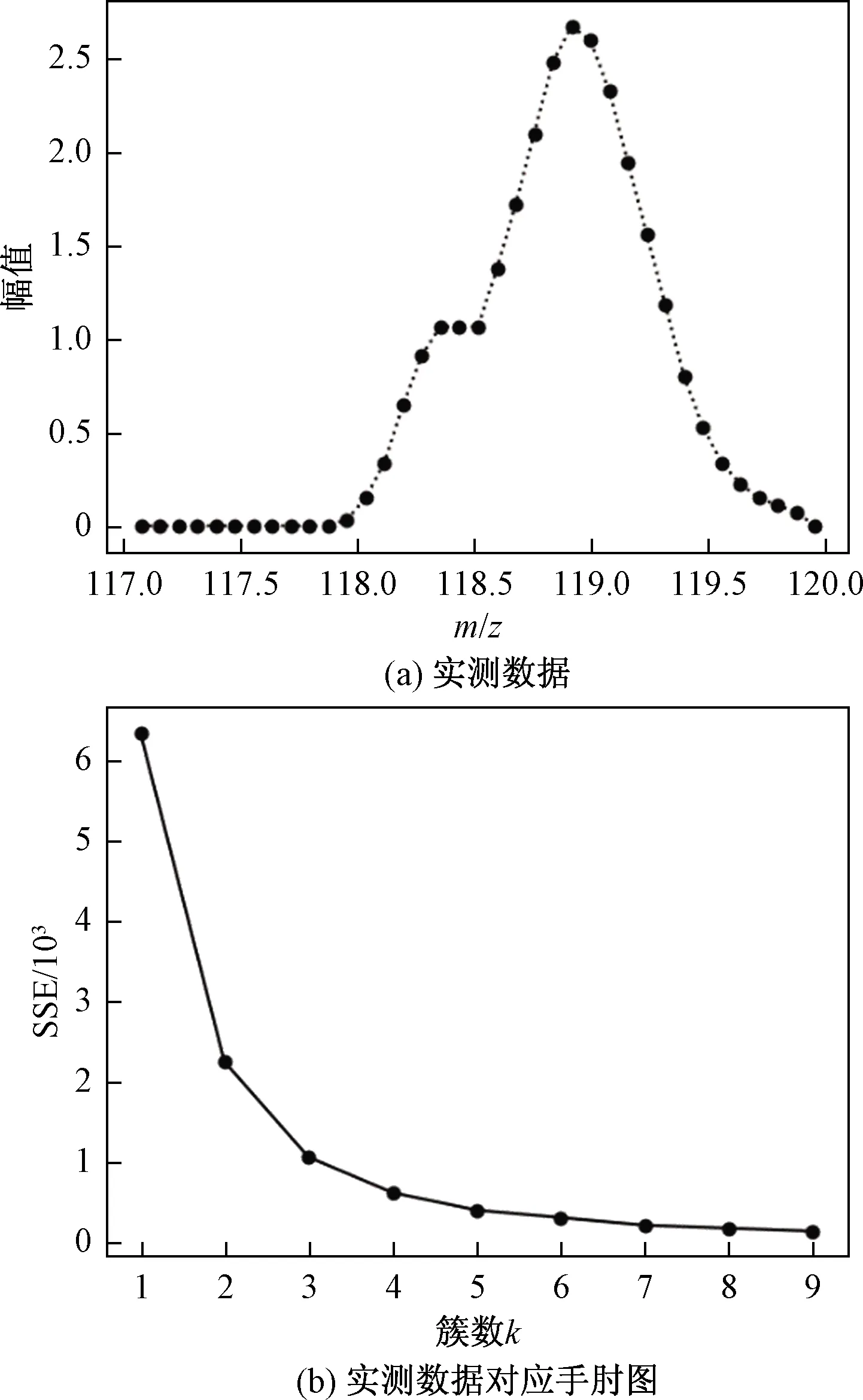
图2 实测重叠峰与手肘图Fig.2 Measured overlapping peaks and elbow diagram
2.3.2 均值和标准偏差的确定
EM算法对初值较为敏感。经验值或随机值可能会导致EM算法的局部收敛。为了避免该问题,可根据谱图在化学量测中的物理意义来设置初值,即质谱图中的信号峰位、峰高和峰宽与高斯函数的均值、幅值和标准偏差有关。如图3所示,采用模拟重叠峰数据给出求初值示意图,均值即为峰幅值处对应的横坐标,可通过寻峰的方式确定初始均值;50%峰高处的宽度(半高全峰宽)等于2.35倍的标准偏差,则根据图3中DE段可确定标准偏差初值。其中,A点和B点是通过寻峰所得峰顶以及对应的横坐标;从B点出发,沿y=0.05(最大幅值1%)水平轴向右,与曲线的第一个交点定为C点;D点和E点分别为线段AB和AC的中点。根据三角形中位线定理得DE等于BC的一半。同理,可设置另一峰的初值。
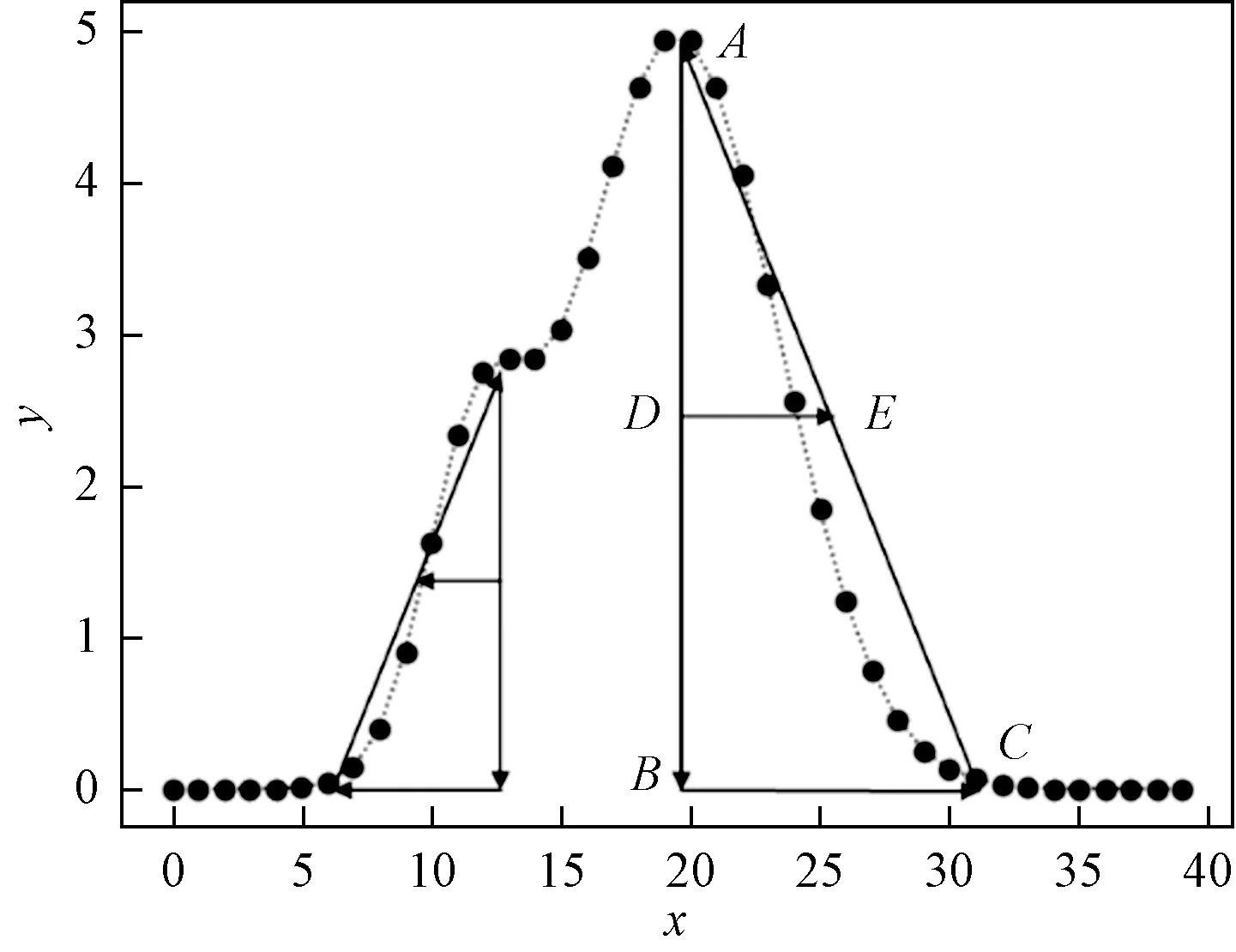
图3 确定均值和标准偏差初值示意图Fig.3 Schematic diagram of determining the initial value of the mean and standard deviation
3 实验结果与讨论
为了评价GMM模型结合EM算法解析重叠峰的效果,引入相对误差、相关系数R2和信噪比三个指标。由于已知模拟重叠峰数据的均值和标准偏差等参数,故本文采用解析前后各参数的相对误差和R2来评价模拟数据解析的效果;对于实测数据,解析前的均值和标准偏差均未知,故采用信号和噪声的EIC比值作为信噪比以及R2来评价实测数据解析结果。
3.1 模拟重叠峰解析
模拟重叠峰是在敞开式质谱仪实测信号的基础上设计的,已知簇数为2,按照小峰与大峰的标准偏差分别为2.5和4,峰位置相差10,峰幅值比为1∶3进行模拟重叠峰信号,抽样次数N=5×104,根据2.2节的方法设置初始均值分别为10.345和19.655,初始标准偏差分别为3和5.5,解析前后的结果如图4所示。从图4(b)中可以看出,解析前后的两个单峰基本重合,相关系数R2均大于等于0.99,没有引起较大峰宽等峰形特征的变化。由此可知,GMM描述重叠质谱信号,然后利用EM算法估计模型参数完成解析的方法是可行的。
3.1.1 重叠峰幅值比例的影响
实验中,在不改变峰宽的前提下,改变模拟大小峰的幅值比来研究其对解析结果的影响,解析前后参数的相对误差如表1所示。从表1中可以看出,采用GMM解析不同重叠情形的模拟数据,解析前后的相对误差指标:均值的绝对值均不大于0.4%,标准偏差的绝对值均不大于2%,即解析后对原始数据峰形影响较小,文中采取的初值设置方法可避免EM算法的局部收敛;另外,解析前后各对应曲线的相关系数都能达到0.99。因此,解析大小峰不同幅值比例的重叠情况时,误差较小,结果可靠。
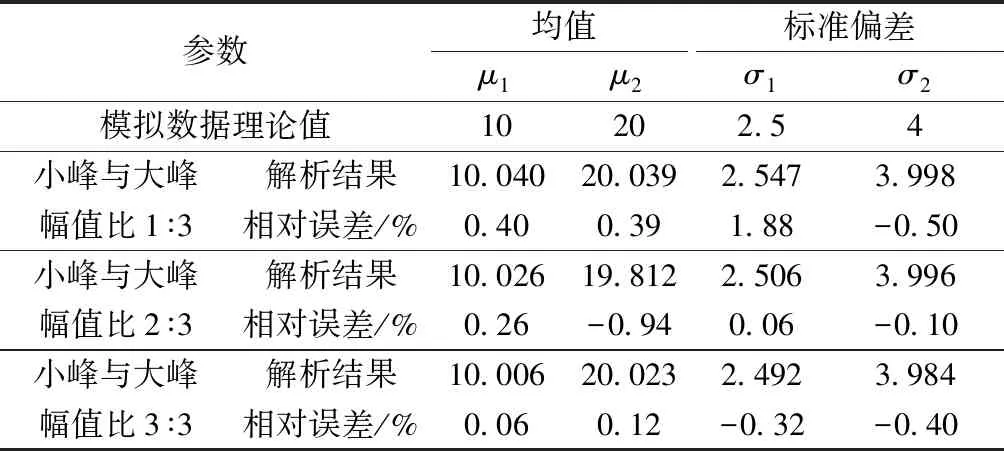
表1 重叠峰不同幅值比解析结果Table 1 Analysis results of different amplitude ratios of overlapping peaks
3.1.2 重叠峰分离度的影响
实验中,在大小峰幅值比为3∶1、峰宽不变的前提下,改变重叠峰的分离度研究其影响。结合质谱理论将色谱中的分离度定义为
(10)
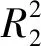
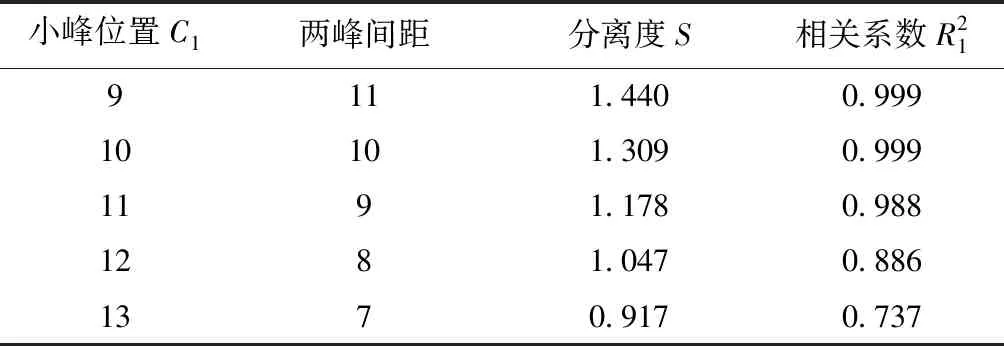
表2 重叠峰不同分离度解析结果Table 2 Analysis results of different resolution of overlapping peaks
叠信号分离度大于1.047。
3.1.3 噪声的影响
实验中,在大小峰幅值比为3∶1、峰位置为20和10、标准偏差为4和2.5的模拟重叠峰基础上,增加不同强度的随机噪声(均值为0,改变方差),观察了噪声对解析结果的影响,解析结果如图5所示,

图5 加入噪声后解析结果Fig.5 Analysis results after adding noise
第一列为加入噪声前后的重叠信号;第二列为加入噪声重叠信号的解析结果。由结果可知,本文所述方法解析重叠峰方法具有一定的抗噪能力;但是,随着噪声的增强,严重影响原始信号的峰形特征,解析重叠峰能力降低。噪声的干扰会影响离散直接抽样产生的随机数据,同时峰形的改变影响初值的设定,进而导致EM迭代计算出现局部收敛问题,无法得到准确的解析结果。
3.2 实测重叠峰解析
对于冰毒碎片离子在m/z=119处的重叠峰信号,获取常见的不同重叠形式的数据进行解析实验。抽样次数N=5×104,初始均值、标准偏差设置分别通过寻峰、峰形的物理意义分别确定,解析后的结果如图6所示。从图6中可以看出,对于这3种不同的实测重叠峰信号,重构后所得GMM曲线与原始实测信号基本重合,相关系数R2均大于0.99,即解析后没有引起峰形的变化,不会影响EIC的计算,解析效果较好。

图6 不同重叠程度的实测数据解析结果图Fig.6 Analysis results of measured data with different degrees of overlap
对于实测数据无法得知构建原始重叠峰的单峰均值和方差等信息,故无法计算得到其相对误差来量化结果。质谱仪常用判断检出的条件是通过信号与噪声的EIC比值即信噪比来设定阈值。未解析重叠峰之前,为了提高结果的准确性,一般计算EIC时选取的隔离宽度较小(如隔离宽度设为1,目标峰在m/z=119,选取的隔离范围为119±0.5)。通过GMM解析重叠峰之后可获取完整的单峰情况,计算EIC时可扩大隔离宽度来增大该值。实测数据解析重叠峰后信噪比结果如表3所示,其中计算EIC的隔离宽度为1。根据表3中解析前后的信噪比会发现,解析后的目标峰EIC在数值上增大,信噪比提高的幅度随着不同重叠形式的信号有所区别,最高可提高10.20%。
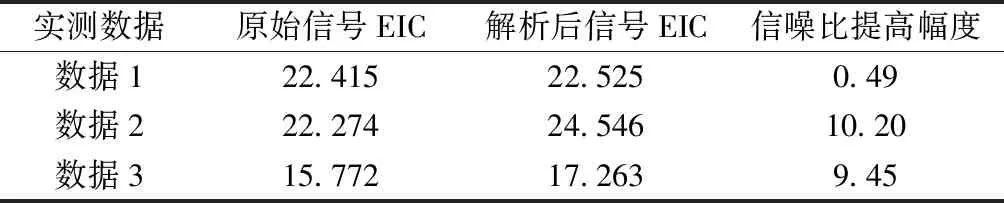
表3 实测重叠峰解析后信噪比Table 3 Signal-to-noise ratio after analysis of measured overlapping peak
4 结论
提出了基于高斯混合模型的解析敞开式质谱重叠峰方法。采用手肘法和质谱图在化学量测中各参数的意义结合三角形中位线定理设置合理的初始参数,然后改变模拟重叠信号的幅值比和分离度、在信号中加入不同强度的随机噪声,对模拟数据和实测不同重叠情况的数据进行解析,通过较好的解析效果验证了该方法可解决敞开式质谱重叠峰问题。相对于传统的信号处理技术,本文方法在分离出目标谱峰信号时不受谱峰对称性的影响,不改变峰形特征,并且该方法具有一定的抗噪声干扰能力。

