于现实的土壤中开出花儿来

西安交通大学附属中学 林逸凡

本教学设计为人教版《数学》选修4-4第二章第一节第1课时的“曲线的参数方程”，对教学环节和教学手段进行了一些创新，现将部分环节与课堂实录予以展示。

一、情境引入

师：参数方程与生活实际密不可分，数学中的许多曲线常常是物体在实际运动中的轨迹。例如：运动员抛掷篮球的轨迹就是抛物线；骑自行车时，如果车轮沾了白色的油漆，那么油漆滚过的轨迹是一条神奇的摆线；日月轮替，星辰自行，太阳系中的行星们每天都在按照自己的轨迹进行公转和自转；日常生活中的面包机、跑步机、按摩椅等，齿轮的啮合转动形成了最优美合适的运动轨迹。大学里为了研究它们，专门开设了一门课程称为“机械原理”。这些运动轨迹中有一把钥匙，那就是——“时间”，其运动规律表现为物体的位置随时间而改变，也就是位置的坐标x，y对时间t的依赖关系。

师：游乐园里类似的例子就更多了，咖啡杯、海盗船、太阳飞车、摩天轮……我们以运动规律最简单的摩天轮为例，按照每20分钟转一圈的匀角速度转动，你能将红色包厢的位置随时间t的运动变化规律很好地描述出来吗？

【设计意图】从实际生活情境出发，小到齿轮零件，大到宇宙星辰，展示与时间密不可分的运动规律，激发学生的学习兴趣，使学生体会数学之美，最后将情境拉到游乐园中的摩天轮，引入最简单的圆的参数方程。

引例：新开的游乐园里有一架摩天轮，非常受大家欢迎。摩天轮的半径为10米，匀角速度转动一圈需要20分钟。思考：观察红色包厢的位置，它与时间t（单位：分钟）的关系是什么？如何用数学语言描述？

师：时间t在这里是一个中介，这个间接引入的变量t就称为参数，单位为分钟。像这样，我们通过研究x，y与t的关系，也就间接建立了x和y的关系式，而这个间接的关系式就是本节课要研究的主题——参数方程。

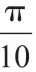
设点：设观察的初始位置为A点，坐标为（10，0），此时t=0。

选参：设动点P（x，y）对应时刻t，由图可知——

检验：其中，t的取值范围为t≥0。

结论：红色包厢的位置可以描述为关于时间t的方程：

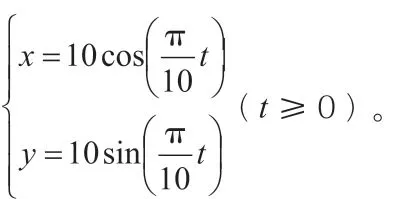
师：值得注意的是，这是θ为锐角时的特殊情形，那么，如果把θ角度的范围进一步扩大，这个式子依然成立吗？

生：当θ为第二象限角时，cosθ＜0，sinθ＞0，与x，y的正负一致，依然符合。同理，当θ为第三象限角时，cosθ＜0，sinθ＜0；当θ为第四象限角时，cosθ＜0，sinθ＜0。

师：按照时间t的物理意义，t的取值范围为？

生：t≥0。

师：那么相应的，θ的取值范围为？

生：θ≥0。

师：但如果要表示一个完整的圆，θ的取值范围应控制在多少？

生：θ∈[0，2π]。

师：以上两个范围都可以。至此，我们成功得到了一个圆的参数方程，其完整的解题步骤为？

生：建系、设点、选参、列式、化简、检验。

师：一个小问题——你能写出这个上半圆的参数方程吗？

生：在原方程基础上添加“θ∈[0，π]”。

师：你能写出这个下半圆的参数方程吗？

生：在原方程基础上添加“θ∈[π，2π]”。

师：我们能说这三个参数方程是一样的吗？

生：不能，要看参数的取值范围。

师：对于一条曲线的参数方程，要满足曲线上的任一点都可以对应到参数方程的有序数对（x，y）解，反过来，参数方程的有序数对（x，y）解所对应的点都在曲线上。因此，在得到参数方程后，必须有双向的检验环节。上述摩天轮包厢运动的分析过程可以推广到一般曲线的参数方程：

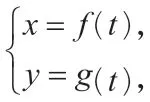
如果对于t的每一个值（a≤t≤b），（＊）式所确定的点P（x，y）都在一条曲线上，而这条曲线上的任一点P（x，y），都可由t的某个值通过（＊）式得到，那么称（＊）式为该曲线的参数方程，其中变量t称为参数。

这个定义中需要加重音的是“每一个”“都在”“任一点”“都可”。

【设计意图】通过对最简单的例子的剖析，在学生脑中自然播入“检验”的思想种子。

变式：（对摩天轮的例子稍作修改）射线OP与x轴的正半轴夹角为30°，Q点从O出发，沿着射线OP方向以速度2运动，依然以时间t为参数，试求Q（x，y）的参数方程。

强调：t≥0，若t∈R，则表示一条直线。

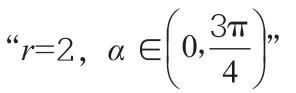
【设计意图】以上强调、思考、辨析、追问四个环节一气呵成，层层递进，在学生的最近发展区做足文章，通过一系列环环相扣的问题串，在非教非授间将本节课的难点化为无形，引导学生重视“明确参数”，注意“参数范围”，培养“检验意识”。

二、概念辨析

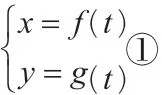
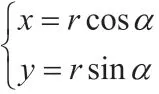
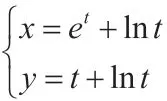
三、典例讲解

例1：小林，小王，小张三位同学将直线方程y=2x+3化为参数方程时，得到了三个不同的式子：

你能说说他们谁做对了吗？

【设计意图】强调参数方程形式的不唯一性、参数的自然范围限制与参数所对应的函数的值域范围限制对轨迹完整性的影响。

学生总结：曲线的普通方程可转化为不同形式的参数方程，但是要注意参数的范围和对应的值域是否彼此等价。

例2：试将下列曲线的参数方程化为普通方程。

【设计意图】再次强调在参数方程与普通方程的互化中，必须使x，y的取值范围保持一致。

学生总结：在参数方程与普通方程的互化中，必须使x，y的取值范围保持一致。

例3：小魔女琪琪以匀速v=15 m/s作水平飞行，若在飞行高度h=24.5 m处投掷包裹（设包裹的初始速度等于琪琪飞行的速度），则：

（1）求包裹离开琪琪后的轨迹方程；

（2）试问琪琪在黑猫吉吉的篮筐多远（水平距离）处投掷包裹，才能刚好投入篮筐？（重力加速度g=9.8 m/s2）

思考1：试将（1）中得到的轨迹方程化为普通方程。

【设计意图】规范解题步骤，体会用参数方程表示轨迹在这个例题中的优越性，同时再次强调范围问题。

例4：试将下列曲线的参数方程化为普通方程。

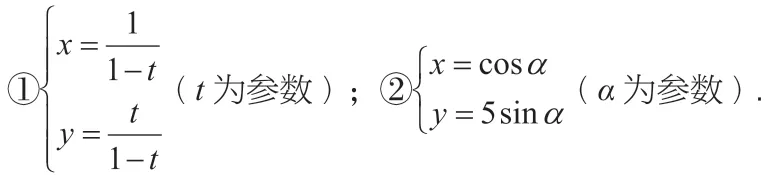
【设计意图】通过例4，进一步强调参数方程的重点、难点，例如，例4的①需要注意函数值域，最后要抠点；例4中的②要注意对tanα是否存在进行讨论，这在全国卷中已经考查过，许多学生都在这里失分，所以需要在新授课特别强调。

四、随堂练习

例5：将下列曲线的参数方程化为普通方程。

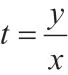
五、归纳提升

谁是参数先明确，

参数范围重点圈。

灵活消参笔头算，

检验意识存心间。

六、课后反思

设计亮点：

1.认真打磨情境引入，扎根现实的背景，用诗意的语言快速激发学习兴趣。

2.重新构建课堂，通过精心设计“问题串”，结合彼此关联的例题及变式，由浅入深，层层递进。

3.给孩子搭建足够大的平台。教师由一个知识霸权者转变为一个问题引导者，激发思维、促使求解自然。

数学是“使人周密的”思维的体操，其课堂是否仅仅只有纯理性这一种打开方式，一个知识灌输的冰冷厂房？能否打破数学“枯燥”“乏味”的刻板印象，给那些原本对数学不感兴趣的学生一个重新爱上它的理由？纸上得来终觉浅，绝知此事要躬行。