一种面向不规则的无线电传播模型下的节点定位算法
葛文庚, 陈 萍
(黄淮学院信息工程学院,河南驻马店 463000)
0 引言
节点定位已成为无线传感网络(wireless sensor networks, WSNs)领域的焦点[1-4],研究人员提出了测距定位算法、非测距定位算法等。测距定位算法虽然精度较高,但因为需要消耗高功率去维持未知节点与锚节点间的通信,而节点常采用小电池容量供电,应用局限性较大。非测距定位算法主要分为两类:启发式和分析式定位算法[5-7]。DV-Hop就是典型的启发式算法,通过未知节点与锚节点间的跳数估计它们间的距离;分析式算法是基于节点具有圆形无线电传播模型假设(radio propagation pattern, RPP)利用理论分析并推导锚节点与未知节点间的距离[6-7]。
文献[8]提出的分布式求精算法,引用“磁极”思想,缩小定位误差,但未考虑无线电传播模型问题;文献[9]提出基于遗传优化DV-Hop定位算法,但该算法与文献[8]存在同样没有考虑到无线电传播模型对定位精度影响的问题。而在真实的传输环境中,常存在信号衰落、阴影以及干扰、各向异性的信号衰减等因素,导致节点的传输模型为非圆形RPP[10]。
为此,提出面向非圆形RPP的基于人工神经网络的加权质心定位算法(artificial neural networks-based weighted centroid localization, ANNs-WCL)。ANNs-WCL算法充分考虑了因非圆形RPP问题,建立新的测距模型,然后再应用人工神经网络修正测距,最后利用加权质心定位算法估计未知节点位置。仿真结果表明,提出的ANNs-WCL算法能够有效地降低均方根误差。
1 网络模型以及问题表述
1.1 网络模型
N个传感节点随机分布于二维网络。考虑全球定位系统GPS的成本,仅部分节点配备了GPS,这些节点知晓自己的位置,为锚节点。而未装备GPS的节点称为未知节点。假定,未知节点的位置坐标为θ=[x,y]T,且θ∈R2。通过m个锚节点估计未知的位置。第k个锚节点的位置为β=[xk,yk]T,且k=1,2,…,m。所有节点的传输半径为R。
1.2 问题描述
非圆形的RPP如图1所示,传感节点分布于面积为S2的区域。实线的圆圈表示圆状的RPP,而虚线表示非圆形的RPP。

图1 网络模型
如果在定位算法中仍假定节点的传输范围是圆形RPP,必然会引起测距误差。因此,考虑利用ANNs系统训练定位模型,修正测距值。
2 测距原理

(1)
式中ni,k表示节点i离锚节点k的跳数;hav表示平均每跳的距离。
对于高节点密度情况,常采用泊松有限理论估计hav,或者引用所有最短路径的平均跳距代替hav。

(2)
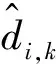
假定节点传输范围为圆形RPP,首先定义重叠区域A,如图2所示。未知节点i以自己位置为圆心,以传输距离R为半径形成的圆表示为D(i,R)。类似地,锚节点k也以自己的位置为圆心,以ni,kR为半径的圆,即D(k,ni,kR)。因此,重叠的圆A的定义如式(3)所示。

图2 重叠区域
A=D(k,ni,kR)∩D(i,R)
(3)

(4)
式中ψ(A)为di,k与A的关系函数;Amin和Amax分别表示A的最小值和最大值;fA(a)为概率密度函数。
利用地理特性和几何知识,可得式(5)[11]:
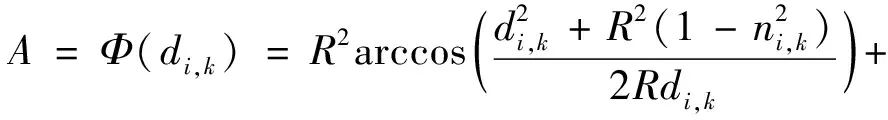


(5)
式中Φ=ψ-1表示ψ的逆函数。由于Φ(di,k)是关于di,k的复杂函数,推导ψ(A)闭合表达式比较复杂。
此外, 假定A均匀分布于[Amin,Amax]。当di,k=ni,kR时,A取最大值Amax;而当di,k=(ni,k-1)R时,A取最小值Amin。因此,可得概率密度函数fA(a)的表达式为:
(6)
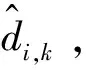
(7)
式中,Φ(1)是Φ的一阶导数。
(8)
3 ANNs-WCL定位
ANNs-WCL定位算法主要由3个阶段构成。第一阶段,未知节点以多跳方式收集信息,然后再利用式(8)估计离锚节点间的距离;第二阶段,利用ANNs修正测距,降低测距误差;最后,利用加权质心定位算法,估计未知节点位置。
3.1 未知节点测距
在ANNS-WCL定位过程中,首先锚节点广播数据包,由首部和数据两部分构成。首部包含锚节点位置,而数据部分存有跳数值,且最初跳数值为1。
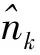
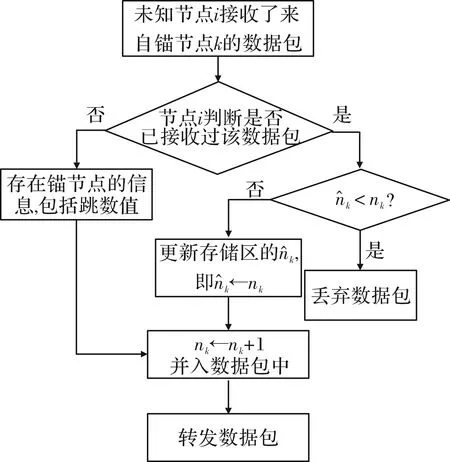
图3 转发数据包的流程

3.2 测距修正
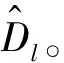

图4 测距修正过程
3.3 加权的质心定位算法
依据3.2节测距修正后,未知节点获取距多个锚节点的距离。再从中选择离自己最近的4个锚节点,即利用测距值最小的4个锚节点构成加权质心定位算法。
假定Aa,Ab,Ac,Ad分别为已选的4个锚节点,相应的,ra,rb,rc,rd分别表示离未知节点i的距离。首先,以锚节点为圆心,以离未知节点的距离为半径画圆,4个锚节点共形成4个圆,有4个交点,假定交点分别为O1,O2,O3,O4。然后,依据这4个交点构成4个不同的三角形,再计算这4个三角形的质心。传统的质心定位算法就是将4个质心坐标的均值作为未知节点的位置。引用加权质心定位算法,即计算每个质心的权值,再依据这些权值,估计未知节点的位置。
以Aa,Ab,Ac这3个圆为例,其交点分别为O1,O2,O3。利用3个圆的半径ra,rb,rc以及3个锚节点Aa,Ab,Ac的坐标(Xa,Ya),(Xb,Yb),(Xc,Yc),可计算3个交点坐标。可利用式(9)所示的方程组中任意两个等式求解交点O1的坐标(XO1,YO1):
(9)
同理可计算其他交点的坐标。计算交点O1,O2,O3坐标后,便可计算这由3个交点所构成的三角形的质心E1坐标(X1,Y1):
(10)
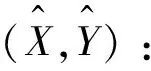

图5 加权质心定位算法
(11)
4 性能仿真
4.1 仿真环境
利用MATLAB7.1软件建立仿真平台,节点随机分布于100 m×100 m区域。节点传输半径为18 m,锚节点数为20。此外,利用文献[10]非圆形的RPP模型,并引用变量不圆形度DDOI。
为了更好地分析ANNs-WCL定位算法的性能,选用同类算法DV-Hop[5]、LAEP[6]和MLPNN-CGFR[12]进行比较。同时,引用均方根误差ERMS作为性能指标:
(12)
4.2 定位的ERMS
首先考查ERMS随节点数N和DDOI的变化情况,实验数据如图6所示,其中图6(a)表示在DDOI=0.06时,节点数N从200变化至800时,ERMS的变化数据;图6(b)表示在N=300时,节点数DDOI从0变化至0.15时,ERMS的变化数据。

图6 定位的归一化的均方根误差
从图6(a)可知,在DDOI=0.06时,ERMS随节点数的增加而下降,节点数增加,获取的网络拓扑信息越多,越有利于定位精度的上升。与DV-Hop[5]、LAEP[6]和MLPNN-CGFR[10]相比,提出的ANNs-WCL算法的ERMS得到有效下降。当N=400时,ANNs-WCL算法的ERMS为0.4 m,而LAEP、DV-hop和MLPNN-CGFR的ERMS分别高达1.31 m,1.1 m,0.98 m。
从图6(b)可知,在N=300时,ERMS随DDOI增加而上升。原因在于:DDOI越高,节点的RPP模型越偏离圆形,测距误差越大,最终,定位精度就下降。与图6(a)类似,与DV-Hop、LAEP和MLPNN-CGFR相比,ANNs-WCL的ERMS仍是最低的。这些数据表明,ANNs-WCL算法能够在真实环境中获取高的定位精度。
4.3 ERMS的CDF曲线
N=300,DDOI=0.06四个算法ERMS的累积分布函数FCDF曲线如图7,且从图7可知,提出的ANNs-WCL定位算法有99%节点获取同一个定位精度,而MLPNN-CGFR只有61%,DV-Hop只有43%,而LAEP仅为30%。这些数据表明,在存在异构信号衰减的环境下,ANNs-WCL定位性能优于同类算法。

图7 CDF曲线
5 总结
针对真实环境中的非圆形RPP问题,提出面向非圆形RPP的基于人工神经网络的加权质心定位算法 ANNs-WCL。ANNs-WCL算法先推理测距表达式,然后利用ANNs修正测距值,最后,利用加权质心定位算法估计未知节点位置。仿真结果表明,提出的ANNs-WCL算法能够有效地降低均方根误差,提高了定位精度。

