基于全球地磁异常场的自主导航仿真系统

田峰敏，卞雷祥，王宏波

(1 南京工程学院，南京 211167；2 南京理工大学，南京 210094)

0 引言

地磁场分为主磁场、异常场和变化场，其中异常场在时间上极为稳定，几乎不随时间变化，含有比地磁主磁场更丰富的细节信息。相比重力测量，地磁测量对载体的运动没有限制[1]，测量设备价格适中，适合作为修正惯导误差的信息源。

Goldenberg介绍了Goodrich公司在飞机上使用磁通门磁力计进行地磁导航的总体方案，并对地磁图制作、载体磁补偿等问题进行了分析[2]。Kato等提出了基于地磁图和等深线图的自主潜航器导航定位算法，并采用相关海域的地磁场数据和水深数据进行验证性分析,得出采用地磁图和等深线图直接定位的效果与用来修正INS的定位效果差不多，且前者受水流影响更小的结论[3]。Canciani利用北美地磁异常数据库和地磁调查飞机的实测数据，进行了地磁异常辅助惯性导航的实验，实验表明地磁图分辨率越高、飞行高度越低、飞行速度越快，定位精度越高，在加州地区根据飞行高度和速度的不同，定位的均方根误差从几十米到几百米不等[4]。穆华等用地磁场作为基准图，提出了基于模标定的地磁测量误差补偿技术，并采用两级滤波算法，底层滤波器估计惯导解算的位置误差，然后将其作为上层滤波器的观测输入，用来估计惯导系统误差。水下实验表明，地磁测量误差补偿技术能够将干扰磁场从 10 000 nT降低至100 nT，能够将600 m的初始位置误差降低至300 m[5]。刘颖等对无人机应用地磁匹配定位和地磁贯续导航进行研究，并设计了原理样机，由于条件限制，并未进行飞行实验，进行了陆面跑车实验，平均定位误差小于2个网格，湖面实验的平均定位误差小于1个网格[6]。吕志峰等设计了地磁匹配导航半实物仿真系统的总体方案，系统分析了地磁场数据库仿真、载体干扰磁场补偿、地磁场环境仿真和地磁匹配导航算法4种关键技术，并提出了相应的工程解决方案[7]。

由于缺乏全球性的地磁异常数据[2]，目前关于地磁导航研究主要集中在方案设计和短距离实验验证，对于采用全球地磁异常场的地磁导航还没有文献进行讨论。

2009年美国NOAA下属的全国地球物理资料中心对卫星测量、航海测量、航空测量的地磁数据进行整理，发布了分辨率为2′的全球地磁异常网格(global earth magnetic anomaly grid，EMAG2)，最新版本为2017年发布的EMAG2_v3[8]，EMAG2为在全球范围内进行地磁导航提供了潜在的数据支持。

文中建立了以EMAG2为基准图的惯性/地磁组合导航仿真系统，用来研究地磁辅助惯性导航的系统模型及算法，为半实物仿真和原理样机的研制提供技术验证。

1 系统结构

如图1所示，组合导航仿真系统按功能结构共分为航迹生成、惯导、航行磁图生成、地磁测量数据生成、地磁推算数据生成、滤波器6个模块。

图1 地磁辅助惯性组合导航仿真系统结构图

1)“航迹生成模块”根据载体的运动指令生成航迹点；

2)“惯导模块”根据航迹点生成惯导运动参数及指示航迹；

3)“航行磁图生成模块”根据载体的运行高度，由基础地磁异常图延拓生成航行地磁异常图；

4)“地磁测量数据生成模块”把航迹点位置在航行地磁异常图中插值生成地磁测量数据的异常场部分，把航迹点位置和时间戳代入国际地磁参考场(international geomagnetic reference field，IGRF)模型生成地磁测量数据主磁场部分，然后计算测量噪声，三者之和为地磁测量数据；

5)“地磁推算数据生成模块”把修正后位置在航行地磁异常图中插值生成地磁异常推算数据，修正后位置和时间戳代入IGRF模型[9]生成主磁场推算数据，二者之和为地磁推算数据；

6)惯导模块输出的纬度、高度、速度、比力、姿态角信息传送至状态方程；把地磁推算数据和地磁测量数据传送至观测方程；由滤波器计算惯导误差的修正值，并反馈至惯导模块，得到载体位置的修正值。

2 方法

2.1 位场延拓

载体的运行高度与基础地磁图的制备高度可能不一致，解决这一问题的方法是位场延拓技术。事先根据航行计划对基础地磁数据进行向上延拓(upward continuation)或向下延拓(downward continuation)，使航行地磁异常图的制备高度与载体的运行高度一致，延拓方法参见文献[10]。

下面给出以EMAG2为基础地磁异常图的延拓试验结果，图2是制备高度海拔4 km处的EMAG2原始数据，图3和图4分别为经向上延拓和向下延拓得到的海拔4 000 m处的地磁异常与EMAG2原始数据之间的差异，都在±2×10-12nT之间。

图2 海拔4 km处EMAG2原始数据三维图

图3 向上延拓海拔4 km处地磁异常的误差

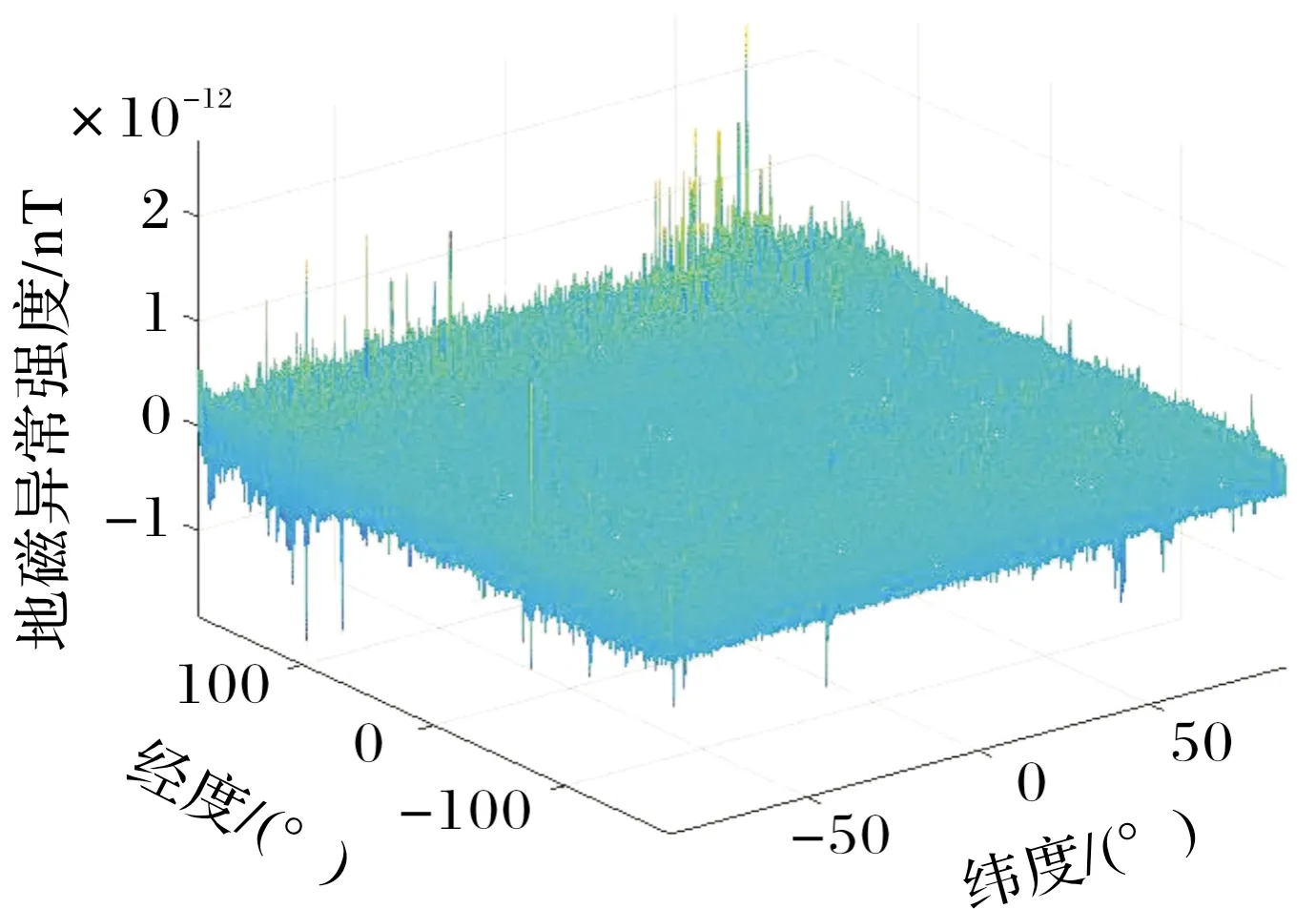
图4 向下延拓海拔4 km处地磁异常的误差

2.2 地磁测量数据和地磁推算数据生成

模拟的地磁测量值由IGRF模型计算的地磁主磁场值、由EMAG2插值生成的地磁异常值、测量误差3部分组成。计算某一位置的地磁异常值，需要进行插值，目前常用的线性插值为C0连续，为了获得更高的连续性，这里采用了自然邻点插值算法[11]，由自然邻点位置地磁异常的凸组合来表示插值点位置的地磁异常，获得了在自然邻点上是C0连续，在Delaunay三角形外接圆边界上是C1连续，在定义域其它地方都是C∞连续的光滑性。

2.3 系统误差模型及求解

在文献[4]和[12-13]的基础上，采用贯序滤波的方式实时估算惯导的位置误差，系统的误差模型由状态传递方程和量测方程组成，选取15阶状态量，包括位置误差、速度误差、姿态误差、加速计测量误差、陀螺仪测量误差。

1)状态量

X=[δLδλδhδυeδυnδυuφeφnφu

∇x∇y∇zεgxεgyεgz]

(1)

式中：[δLδλδh]为载体位置误差；[δυeδυnδυu]为本地坐标系下速度误差；[φeφnφu]为姿态误差角，即数学本地系与真实本地系之间的夹角；[∇x∇y∇z]为加速度计零偏；[εgxεgyεgz]为陀螺仪漂移[4,13]。

2)状态方程

(2)

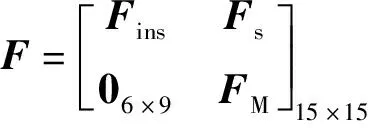
3)测量方程

(3)

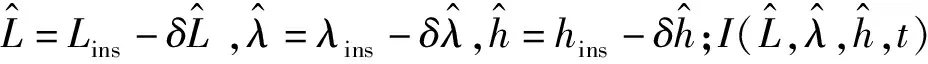
4)离散化的系统状态方程和量测方程

Xk=Φk,k-1Xk-1+Γk-1Wk-1

(4)

(5)

当采样周期Δt较小时，式(2)中的F(t)和G(t)可以看作是非时变的，此时状态转移矩阵Φk,k-1、误差传递矩阵Γk-1可由下式计算。

(6)

(7)

式中：E(Wk)=0,E(WkWj)=Qkδkj,Qk=Q(t)/Δt；E(Vk)=0,E(VkVj)=Rkδkj,Rk=R(t)/Δt。

5)滤波器

式(1)～式(7)推导了地磁辅助惯性导航系统的状态方程和量测方程，其中量测方程为非线性方程，采用无迹卡尔曼滤波(unscented kalman filter, UKF)作为系统误差模型的求解方法。

3 仿真验证

测试条件：载体先以1g的加速度作20 s的加速，接着爬升至10°仰角并匀速飞行10 s，然后恢复平飞，再继续加速10 s然后作2个90°转弯，最后俯冲，运动持续392 s，飞行距离约139 km，飞行轨迹见图5。采用了A、B、C三种不同精度等级的惯导，惯导及磁力计参数见表1，量测更新周期为1 s。仿真试验基于EMAG2全球地磁异常数据，网格分辨率为2′(≈3.7 km)。表2是三组试验结果的统计，图5～图6是仿真过程展示。

表2 地磁导航仿真结果

图5 地磁修正后航迹与3组惯导指示航迹的对比

图6 线性插值地磁导航和自然邻点插值地磁导航对3组惯导误差的跟踪

从图5和图6可以看出，在纯惯性导航条件下的位置误差在200 s之后开始发散，最多达到22.5 km，采用地磁异常进行修正后，线性插值地磁导航和自然邻点插值地磁导航都可以跟踪惯导误差，但后者位置误差的最大值、均值、方差、均方根都优于前者。从表2可以看出，根据惯导精度的不同，采用自然邻点插值地磁导航后，位置误差最大值可控制在0.3～1.7个网格以内，位置误差均方根可控制在0.1～0.7个网格以内。两种插值滤波方法单点滤波耗时都小于0.1 s，满足1 s的量测更新周期。

4 结论

设计了基于全球地磁异常场的地磁/惯性组合导航仿真系统，经过仿真试验验证，得到两个结论：

1)基于全球地磁异常场的地磁辅助惯性导航方法，可以有效降低累积误差，提高定位精度；

2)在地磁辅助惯性导航滤波器中，采用自然邻点插值逼近任意位置地磁异常曲面比采用传统线性插值方法能获得更好的滤波效果，且运算耗时没有明显增加，适合作为地磁异常辅助惯性导航的滤波算法。

EMAG2全球地磁异常场由海测、航测、卫测多种数据加工处理而成，官方并没有给出数据的具体精度，根据常理推断在小范围内其数据精度无法与实测数据相比，但作为大范围的平均值，其精度还是可信的。为满足自主导航的需要，这个范围怎么取取多大，有待进一步的理论研究和实物验证。