电磁轨道发射装置的动态多物理场耦合分析

杨 帆，翟小飞，张 晓，刘 华

(海军工程大学舰船综合电力技术国防科技重点实验室，武汉 430033)

0 引言

伴随着电枢的高速运动，电磁轨道发射装置内电磁场、温度场和结构场相互耦合在一起，使装置内弹道工作环境十分恶劣[1]。为了设计出既能保证枢轨间有足够的接触力而不发生转捩，又能保证不会因温度过高、受力过大而产生破坏的电枢结构，研究发射状态下的内弹道多物理场耦合模型十分必要。

目前对构建电磁轨道发射装置的多物理场耦合计算模型已取得了一定成果：在国外，一些计算程序如EMAP3D[2]，MEGA[3]和HERB[4]等被开发出来，用于模拟高速滑动电接触条件下的电磁-温度-结构耦合，并得到了一些基本规律。在国内，谭赛等[5-6]采用自由度平移法建立了考虑摩擦热的电磁-温度-运动耦合场有限元数值计算模型，并与由EMAP3D所得的结果相吻合，但没有对结构场进行耦合计算。Lin等[7]利用Ls-dyna软件，基于有限元和边界元耦合计算的方法，求解了电磁发射过程中电枢和导轨上电流密度、温度和应力的分布情况，但该模型只进行了单向耦合分析，且没有考虑材料的非线性问题。

COMSOL Multiphysics软件可以用于多物理场耦合仿真，该软件的突出优点是各物理场可在一套相同的网格节点中进行双向耦合计算。田振国等[8]和郑杜成等[9]均通过该软件构建多物理场耦合模型，以计算导轨上的应力分布情况。但前者没有考虑速度趋肤效应带来的影响；后者仅通过“移动电导率”的方式处理电枢运动问题，忽略了电枢结构带来的影响。王世礼[10]、张占群[11]详细介绍了动网格移动方法的种类及特点，采用基于Laplacian方程映射的动网格移动方法能够有效保证结构体边界上网格的质量，有利于提高模型的收敛性和准确性。

针对上述模型中存在的不足，通过COMSOL Multiphysics软件，采用基于Laplacian方程映射的动网格移动方法处理电枢运动问题。在考虑材料非线性的同时，构建电磁轨道发射装置电磁-温度-结构耦合场的三维瞬态有限元模型。最后经模型计算，得到在电枢运动情况下的电流、温度和应力的分布特点。

1 理论计算方程

电磁轨道发射装置的工作原理[12]如图1所示，电流由上导轨流入，经过电枢从下导轨流出，形成一闭合回路。电流经过导轨时在膛内产生磁场，与流经电枢的电流相互作用产生洛伦兹力加速电枢运动。

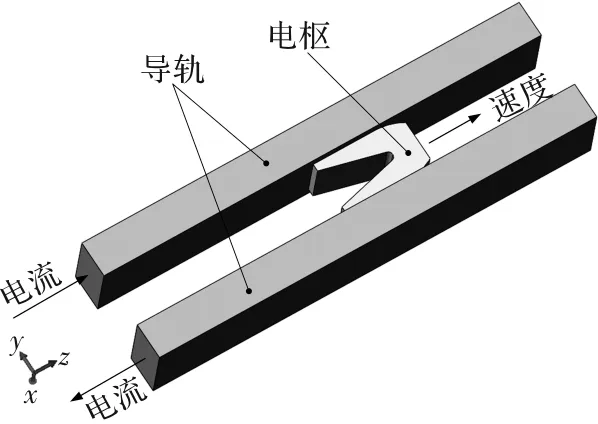
图1 电磁发射工作原理图

电磁轨道发射装置内多物理场耦合关系如图2所示。电磁场中产生的电磁力和焦耳热在电枢和导轨上的分布，分别影响着结构场中的应力和温度场中的温度在电枢和导轨上的分布情况；温度场中产生的温升会降低电枢和导轨材料的电导率和抗拉/屈服强度，进而分别影响电磁场中产生的焦耳热和结构场中的应力应变；结构场中电枢高速滑动产生的摩擦热是温度场中温升的热量来源之一，枢轨接触面上的接触力分布影响着电磁场中电流密度在枢轨接触面上的分布情况。

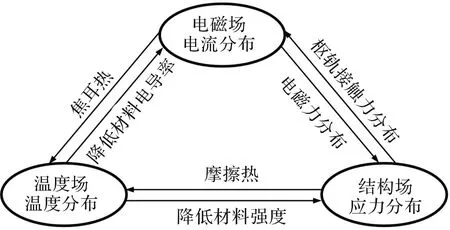
图2 多物理场耦合关系图

1.1 电磁场控制方程

建立由电磁感应定律、安培环路定律和欧姆定律为基础的电磁学控制方程，其微分形式分别为：

(1)

(2)

J=σE

(3)

式中：E,B,J分别为电场强度,磁感应强度,电流密度；μ为材料的磁导率；σ为材料的电导率；v为电枢速度，只有z轴方向上有分量ν。

将式(1)～式(3)联立，可以得到用于计算磁感应强度和电流密度分布与扩散的方程：

(4)

电枢和导轨所受洛伦兹力的计算方程为：

(5)

其中V为结构体的体积。

在不考虑电枢受到的摩擦力和空气阻力的情况下，电枢的速度与位移方程为：

(6)

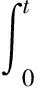
(7)

式中：Fz为电枢受到的电磁推力，即洛伦兹力在z轴方向上的分力；ma为电枢质量；t为时间；wa为电枢位移;w0为电枢在导轨上的初始位置。

1.2 温度场控制方程

如果只考虑电流焦耳热作用，忽略接触电阻焦耳热和摩擦热，导轨和电枢内的热传导方程可写为：

(8)

式中：T为温度；j为电流密度模；ρ,c,κ分别为材料的密度,比热容和热传导系数。

1.3 结构场控制方程

基于动量守恒的结构场控制方程以张量的形式表达为：

(9)

s,f，w分别表示应力张量，单位体积力和位移。

当电枢和导轨产生温升或温度分布不均时，结构体将产生热应变：

εT=αΔT

(10)

式中：α为材料的热膨胀系数；ΔT为温升。

1.4 基于Laplacian方程映射的动网格移动

基于Laplacian方程映射的动网格移动方法，是一种基于有限元法的网格移动方法。其核心是将结构体视为一弹性固体，对结构体进行网格划分，当结构体的边界移动时，结构体内部网格节点的位移满足Laplacian方程。即当结构体边界移动时，内部网格节点会相应的产生位移从而使网格移动。

当结构体边界移动时，以求解内部网格节点在z轴方向上的位移w为例，其满足的泛函形式方程为：

(11)

在有限元计算方法中，网格节点位移以矩阵形式表示为：

w=Nae

(12)

式中:N为插值函数矩阵;ae为节点位移矢量。式(12)两端分别对x，y，z取偏导可得：

(13)

Ni表示节点i处的插值函数，假如用四面体网格划分结构体，则每一网格上有4个节点，所以i分别取1,2,3,4。

对式(11)中的泛函取变分，并将式(13)代入，则有：

Kae=0

(14)

式中：K为n×n的矩阵，n为网格节点的数量。通过把结构体的边界位移代入到式(14)中，便能求解出结构体内部网格节点在z方向上的位移。依此求解过程，可以计算出节点在x和y方向上的位移。

2 计算模型及仿真设置

2.1 计算模型

如图3所示，为电枢和导轨的几何模型及网格划分。导轨为长方体结构，长0.9 m，宽40 mm，高20 mm，间距30 mm，材料为铜合金。电枢为C型结构，材料为铝合金，电枢质量ma=81.46 g。初始时刻，电枢末端距离导轨末段为0.12 m，枢轨接触面长度为36 mm，因此初始时刻枢轨接触面前端距离导轨末端为0.156 m，并将此长度范围内的导轨部分记为导轨1。在电枢运动过程中，即将与电枢接触的导轨部分记为导轨2。材料的电导率和屈服强度会随着温度的升高而降低，相关材料随温度变化的性能参数如表1所示。

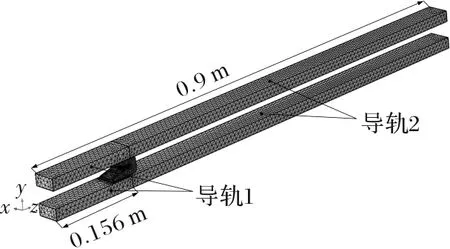
图3 电枢和导轨的几何模型

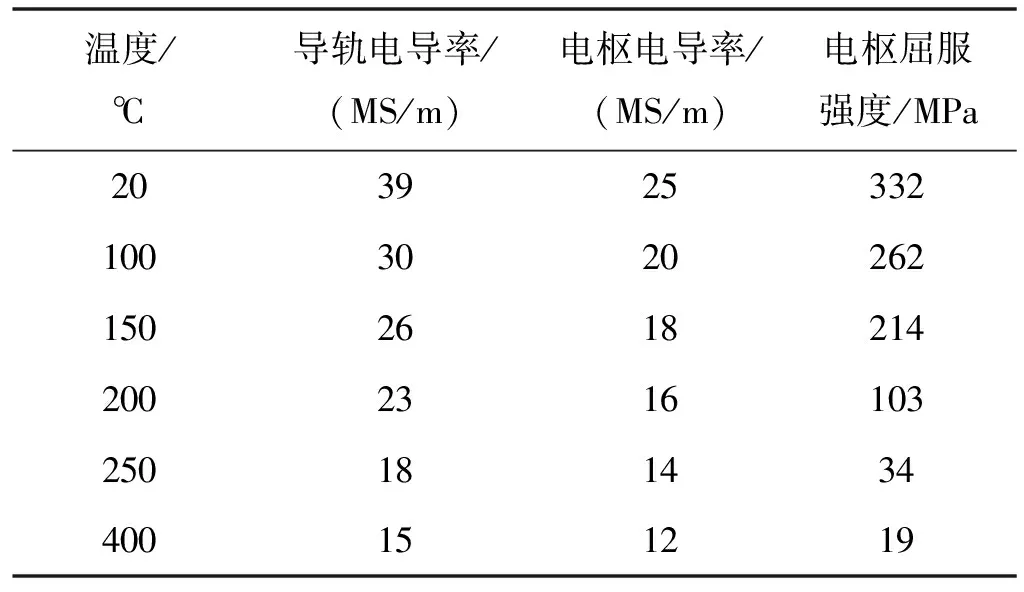
表1 材料性能参数

通入导轨和电枢的激励电流如图4所示，峰值电流为200 kA，峰值电流时刻为2 ms，激励时间为3 ms。

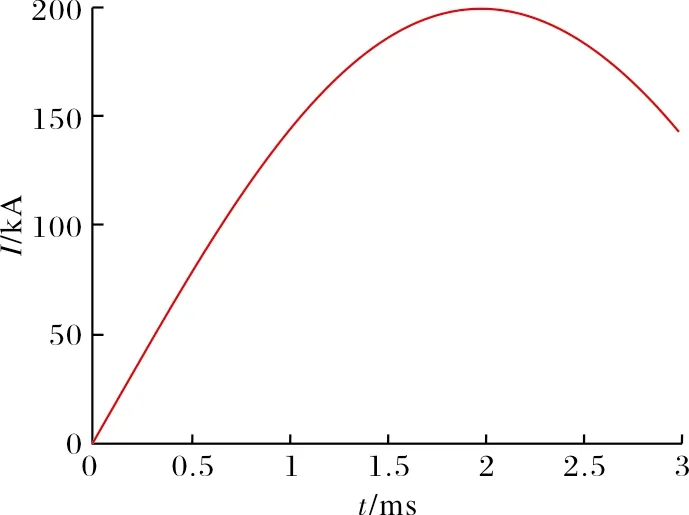
图4 激励电流曲线

2.2 仿真条件及设置

为简化计算，仿真过程中作如下假设：不考虑电枢磨损带来的影响；不考虑接触电阻焦耳热和摩擦热的影响；不考虑摩擦力和空气阻力对电枢运动带来的影响；初始时刻电枢与导轨接触均匀。

在COMSOL Multiphysics中添加“磁场”、“电路”、“固体传热”、“固体力学”、“电磁热”和“热膨胀”等物理场接口，同时设置“动网格(ALE)”接口用于计算电枢动态发射过程中的多物理场耦合问题。

如图3所示，用四面体网格划分几何体。在“动网格(ALE)”接口设置中，电枢的边界位移wa由式(7)决定，其中电枢受到的电磁推力Fz由“磁场”接口计算得到。导轨1和导轨2在电枢运动过程中所设置的边界位移w1和w2分别为：

(15)

(16)

Z为z轴上的坐标值，单位为m。

3 仿真结果及分析

仿真计算得到电枢在所受电磁推力作用下的速度、位移曲线如图5所示，电枢最大位移为0.75 m，出口最大速度为450 m/s。

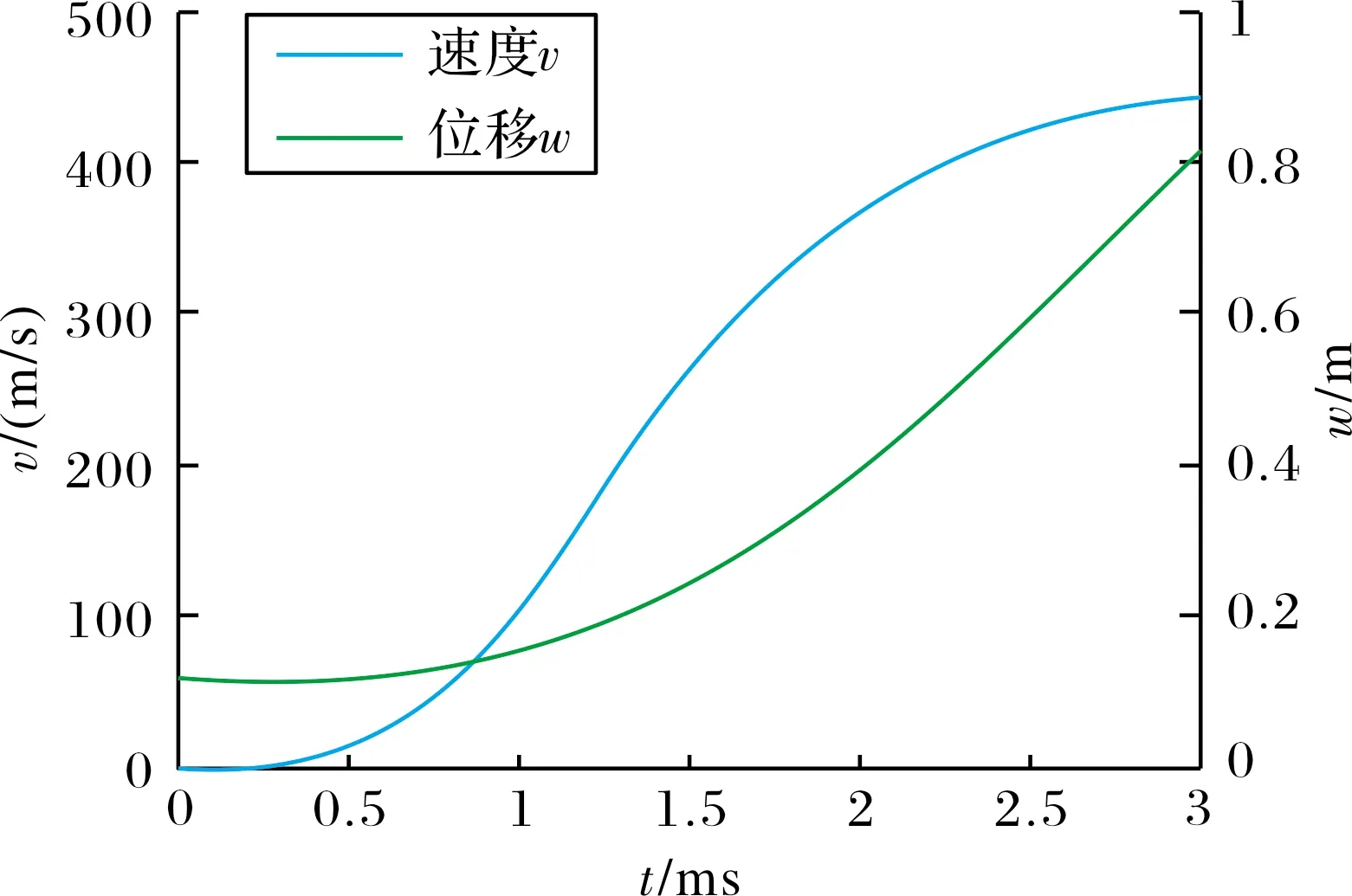
图5 电枢的位移和速度曲线

3.1 电磁场仿真结果

发射过程中，电流密度和磁感应强度在电枢和导轨上的分布如图6～图7所示。受速度趋肤效应的影响，电枢和导轨内的电流密度和磁感应强度呈现出相同的分布规律：电流密度与磁感应强度主要分布在导轨内侧与电枢后侧的表层部分，并分别向导轨外侧和电枢前侧扩散；电流密度和磁感应强度更集中于枢轨接触面的后侧；对于C型电枢结构，电流密度和磁感应强度集中在电枢臂转角处的喉部分布，该位置处电流密度和磁感应强度的值最高。

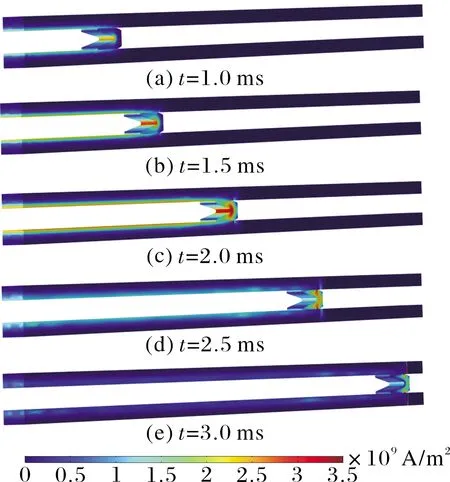
图6 电枢和导轨内的电流密度分布

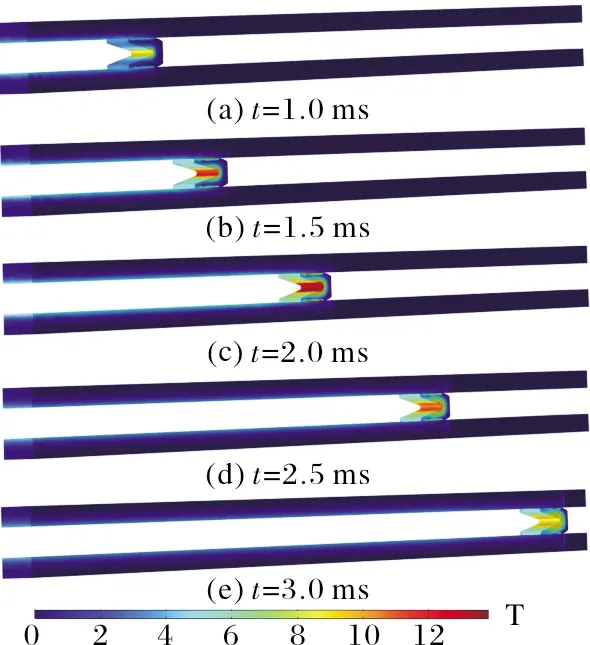
图7 电枢和导轨内的磁感应强度分布

图8为1.5 ms时洛伦兹力密度在电枢和导轨上的分布情况，洛伦兹力密度分布与电枢和导轨的结构有关。对长方体导轨，在宽度方向上洛伦兹力密度均匀分布；在长度方向上，越靠近枢轨接触面后侧，洛伦兹力密度越大，这是因为该位置处电流密度集中。对于C型电枢结构，洛伦兹力密度垂直于电枢臂分布，既有推动电枢前进的分力，又有使电枢外扩以保持枢轨良好接触的分力。

图8 1.5 ms时洛伦兹力密度分布

3.2 温度场仿真结果

不同时刻电枢和导轨上的温度分布如图9所示，高温区域主要集中于电枢的喉部和枢轨接触面上。这是电流密度集中造成焦耳热增大所导致的。电枢是载流元件，在焦耳热的作用下，随着时间的增加，电枢在发射过程中的温升会越来越大。出口时刻，电枢最高温度已达386 ℃。

图9 不同时刻电枢温度分布图

图10为动态发射过程中不同时刻热功率密度在电枢上的分布情况。从图中可以看出，热功率密度分布首先出现在枢轨接触面上的后侧，随着时间的推进，逐渐沿着电枢长度方向向接触面的前侧集中。这是由速度趋肤效应作用所产生的熔化波烧蚀现象[7,13]。

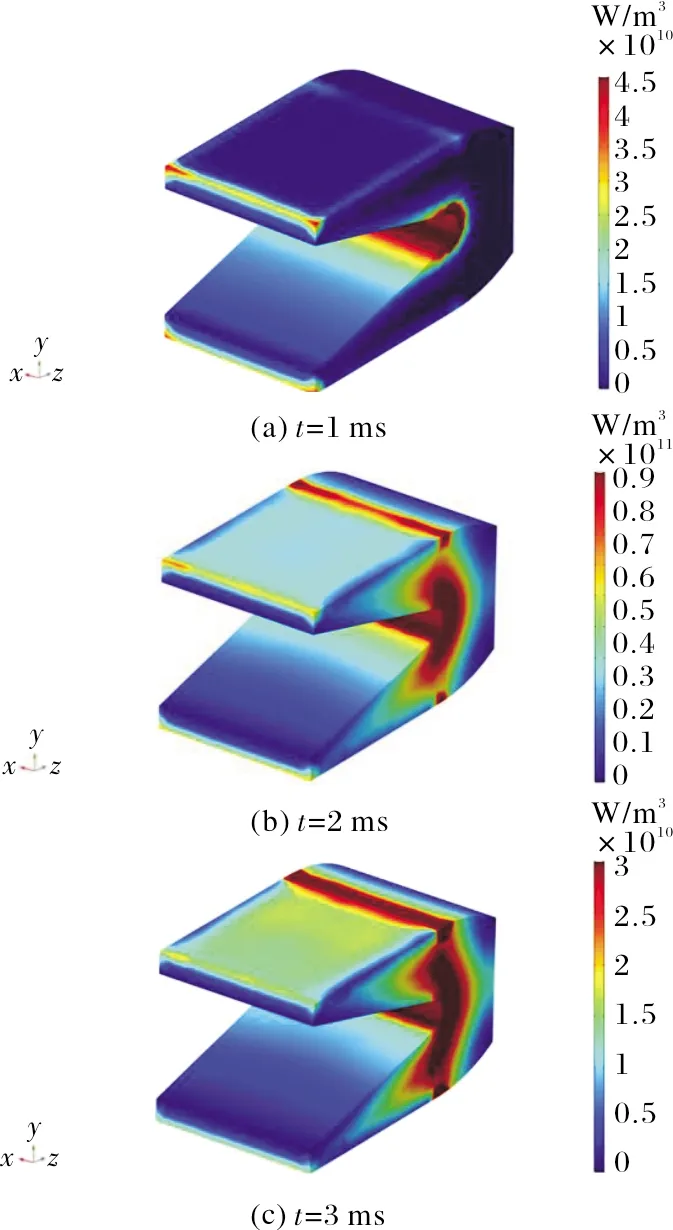
图10 电枢上热功率密度分布

3.3 结构场仿真结果

电枢和导轨上应力分布如图11所示，不同时刻电枢上的应力主要集中在电枢喉部区域，这是因为电枢喉部电流密度最大。峰值电流时刻即2 ms时，喉部区域最高应力为422 MPa。对比图9可以看到，在不同时刻电枢喉部区域的温升也最高，造成电枢喉部区域抗拉强度和屈服强度的下降。如果电枢喉部区域所受到的平均应力高于该位置平均温度下的屈服强度，则会导致电枢的变形甚至是断裂。

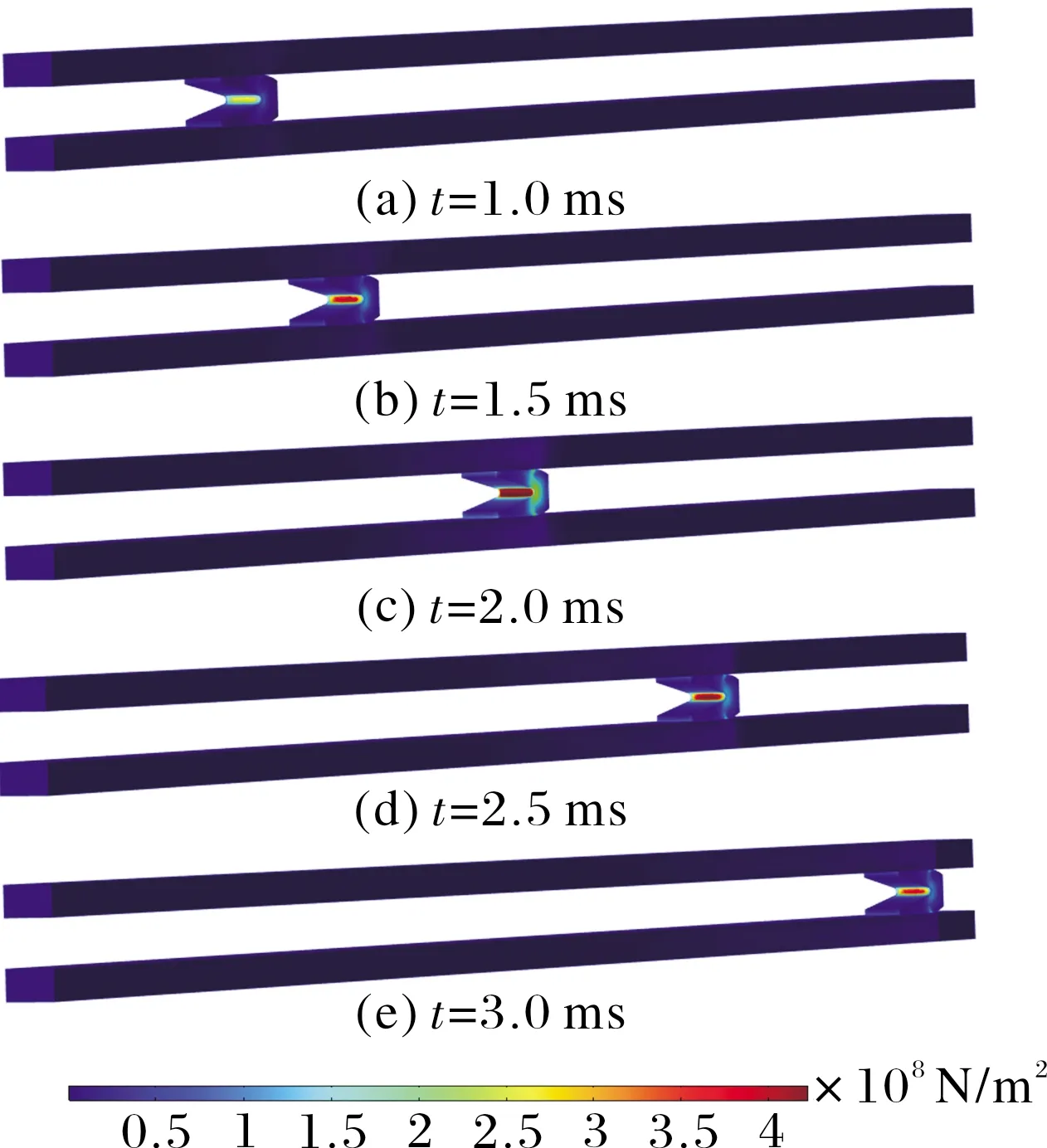
图11 电枢应力分布

4 结论

通过构建电磁轨道发射装置的动态多物理场耦合计算模型，仿真计算了电流密度、温度、应力等物理量在电枢和导轨上的分布情况。在所构建的有限元计算模型中，各物理场通过一套相同的网格节点进行直接耦合计算，能够得到受速度趋肤效应影响的电磁扩散和熔化波烧蚀等在电磁轨道发射中出现的典型现象。仿真结果表明，构建的仿真模型对描述和解决电磁轨道发射多物理场耦合问题是可行的，可以为电枢的优化设计工作提供一定的指导。