客车侧翻仿真中初始位置选取对结果的影响

酒军亮， 赵立新， 詹国臣， 王小伟， 梁奇伟

(1.金龙联合汽车工业(苏州)有限公司， 江苏 苏州 215026;2.陆军装备部驻南京地区军代局， 上海 200031)

随着GB 17578—2013《客车上部结构强度要求及试验方法》[1]的强制实施，采用计算机仿真方法代替实车进行侧翻试验验证，因其具有周期短、成本低和风险小的优点，成为各大客车厂家首选的认证方法。由于仿真精度是决定结果是否有效的重要因素，所以针对计算机仿真精度方面的研究显得尤为重要。本文对客车侧翻仿真分析中的初始条件选取进行深入研究。

1 侧翻仿真初始条件确定

依据GB 17578—2013[1]的要求，侧翻试验车辆从临界侧倾位置开始，在重力作用下翻滚撞击到地面，通过窗立柱变形量来判定乘员生存空间的侵占情况。在未接触地面前，车体没有发生塑性变形，不是关注的重点。在仿真分析中为提高仿真效率，目前大多选取车体刚接触地面的瞬间作为仿真的初始时刻，而该 “瞬时”位置的初始角速度目前又大多采用以下方法计算：

客车从临界侧倾位置到接触地面的瞬间，设质心的垂直位移为Δh，Δh=h1-h2,h1、h2分别为客车在临界侧倾位置和接触地面瞬间的质心离地高；客车在临界侧倾位置的角速度为ω0(此时车辆绕自身翻转轴的角速度为0。本文考虑侧翻台架角速度≤5°/s的要求[1]，设置ω0为5°/s(0.087 rad/s)以得到较为苛刻的仿真结果)。根据能量守恒定律有[2]：

(1)

式中：m为客车的总质量；g为重力加速度；ωt为客车刚接触地面瞬间的角速度；J为客车侧翻转动惯量。

式(1)中的J值在仿真分析中的获取过程如下：首先在LS-DYNA仿真软件中，通过已建立的客车侧翻仿真模型计算出模型质心离地高h1和h2，得到Δh；然后设置一个确定的角速度值ωk试运算，仿真软件会计算出对应的动能为Ek，再由公式Ek=Jωk2/2手工计算出车体的转动惯量J：

J= 2EK/ωk2

(2)

将式(2)计算出的转动惯量带入式(1)，即可手工计算出车体刚接触地面瞬时的角速度ωt作为仿真分析的角速度输入值。

当仿真分析的初始位置选取在临界侧倾位置与车体刚接触地面之间的任一位置时，其仿真输入的初始角速度ωi都可采用上述方法计算。ωi作为侧翻仿真分析最重要的边界条件，其准确性对结果的可信度影响很大。本文通过下述分析，说明以上传统方法计算ωi用于仿真的不准确性问题。

2 仿真分析位置设置及结果分析

2.1 仿真位置设置及分析

将客车的临界侧倾位置作为标准的侧翻仿真分析位置，得到的仿真结果作为标准的仿真值与其他仿真分析开始位置结果进行对比。以某公路客车实际结构为研究对象,设定3个仿真初始位置，第1侧翻仿真初始位置为“标准”位置，计算得知其侧倾临界角为35.7°；第2、3侧翻仿真初始位置分别在“标准”位置的基础上将车体旋转40°和68°；其中第3侧翻仿真初始位置为车体刚接触地面瞬间的位置，应该为侧翻仿真分析最迟开始的位置。第1、3侧翻仿真初始位置如图1所示。

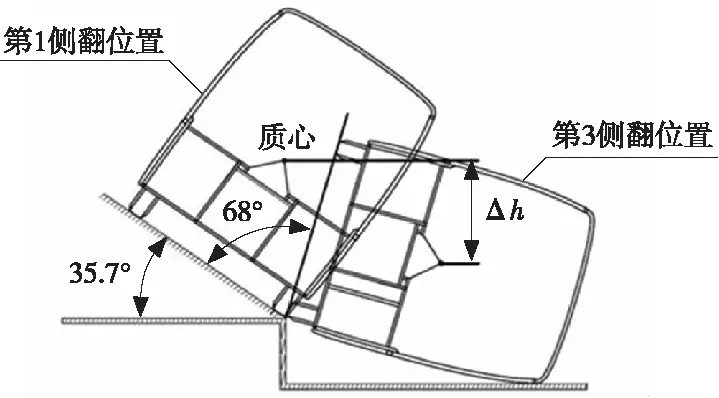
图1 第1、3侧翻位置

仿真建模过程中的结构简化、质量处理、网格划分、单元选择、材料选择以及载荷处理等均按照较成熟的方法进行[2-6]，最终建立的整车仿真模型如图2所示。上述的第1侧翻仿真初始位置，共计 455 144 个节点，487 569个单元，其中壳单元471 493个，实体单元1 335个，质量单元14 741个。将该仿真模型按前述旋转可得到第2、3侧翻仿真分析的初始位置。

图2 整车有限元模型

按照式(1)和式(2)计算，3个侧翻仿真初始位置的初始角速度为：ω1=ω0=0.087 rad/s，ω2=1.224 rad/s，ω3=2.065 rad/s。按照文献[7-8]介绍的方法，在LS-DYNA仿真分析软件中设置求解时间、接触控制、沙漏控制以及输出控制等，其中求解时间分别设置为2.5 s、0.8 s和0.25 s。

2.2 仿真结果分析

按照GB 17578—2013[1]要求布置乘员生存空间的测点位置，所有测点均位于碰撞侧立柱上，见图3。

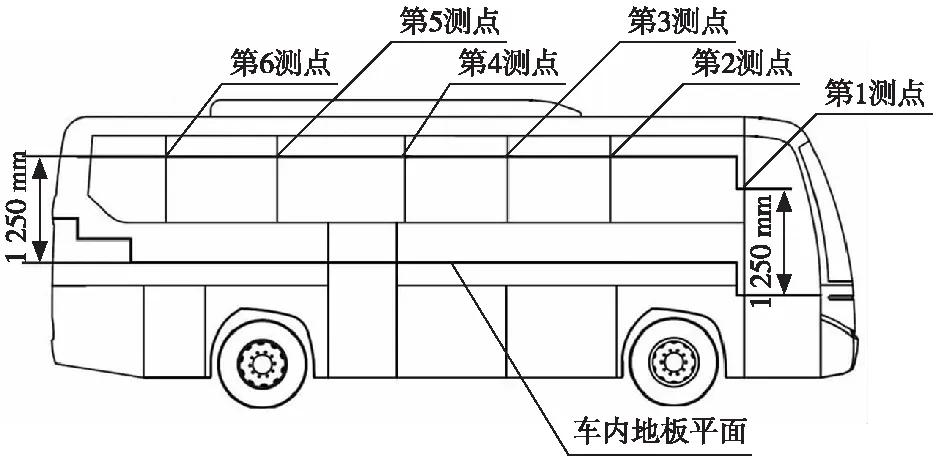
图3 测点位置布置

2.2.1 变形分析

3个仿真初始位置的侧翻仿真模型除求解时间和初始角速度不同外，其余所有参数均相同。由3个仿真模型的最大变形图可知，第1侧翻仿真初始位置的变形最严重，第2侧翻仿真初始位置次之，而第3侧翻仿真初始位置最小。与“标准”位置相比，第2、3侧翻仿真初始位置车体的生存空间被侵占的情况逐渐变小，说明第2、3仿真分析方案的仿真结果趋于保守，特别是第3侧翻仿真初始位置，乘员生存空间被侵占的情况不太明显，与“标准”情况差别较大。其中第1、3侧翻仿真初始位置仿真的最大变形如图4所示。

(a) 第1侧翻位置

表1为依据图3的测点位置得到的立柱变形量。在车体未变形前，各测点距生存空间的最短距离为380 mm。由表1可知，第1侧翻仿真初始位置车体的第4、5、6测点，第2侧翻仿真初始位置车体的第5、6测点和第3侧翻仿真初始位置车体的第6测点的变形量均超过380 mm。由此可见，选择不同初始位置开始仿真得到的计算结果明显不同。误差最大的是第3侧翻仿真初始位置的第1立柱，与标准位置相比误差达到了40.13%。

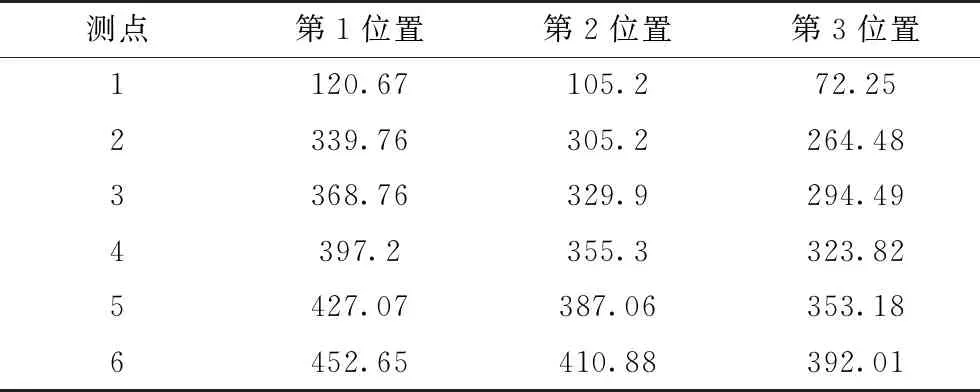
表1 不同仿真分析初始位置的立柱变形量 mm

2.2.2 加速度分析

在客车侧翻过程中，加速度曲线能较综合地反应车辆受到的碰撞力情况。在无假人和乘员约束系统的车身耐撞性模拟分析中，可以将车体加速度作为乘员头部所承受的加速度来间接评价乘员的损伤，过大的加速度峰值和过长的峰值持续时间将引起车内乘员的更大伤害。

图5为3个侧翻仿真初始位置仿真模型的质心加速度变化曲线。加速度峰值依次为62.062g、50.6512g和27.837g。由于仿真时间不同，加速度曲线变化形式有所差别，其中第1侧翻仿真初始位置只有在车体撞击地面后才产生加速度峰值。不难发现，仿真初始位置越靠近地面，仿真得到的加速度峰值越小；反之越大。因此，从侧翻碰撞仿真结果保守性考虑，侧翻仿真初始位置应选取临界侧倾位置。

(a) 第1侧翻位置

(b) 第2侧翻位置

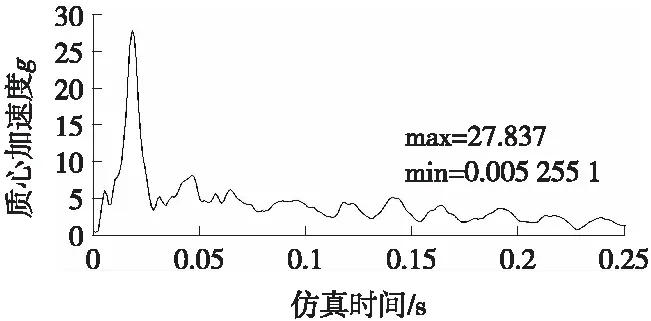
(c) 第3侧翻位置

3 原因分析及改善措施

3.1 原因分析

由上述的车体变形和加速度分析结果可知，第2、3侧翻仿真初始位置仿真得到的结果与“标准”位置的结果偏差较大。3个初始位置的边界条件设置只有初始角速度和仿真持续时间不同，而仿真持续时间与过程无关，说明初始角速度是造成误差的原因。

事实上，通过上述“标准”位置的侧翻仿真分析，LS-DYNA软件可以较准确地提取出车体分别经过第2、3侧翻位置时的角速度，可将该方式得到的角速度作为“准确值”进行对比，结果见后表2中第2栏数据。可以看到，完全用仿真软件得到的角速度与式(1)和(2)计算结果差别较大，特别是第3侧翻位置偏差了37.8%。

式(1)和(2)中转动惯量相等的前提条件是车体有固定的旋转轴。但仿真或实车侧翻时，车体从临界侧倾位置开始向下翻滚，并不是完全绕固定旋转轴转动，而是类似自由落体运动。而车体的转动惯量又与车体的运动姿态和旋转轴有关，即事实是式(1)和式(2)中的转动惯量是不完全相同的，这正是造成理论计算与仿真计算偏差的主要原因，从而导致第2、3仿真初始位置的结果与“标准”位置存在偏差。

3.2 改善措施

为保证各侧翻位置仿真的结果与“标准”位置相近，需要提高各侧翻仿真位置初始角速度的精度，可通过下述3种方法进行改善：

方法一：在仿真求解前，完全直接用LS-DYNA软件仿真计算出各仿真初始位置的角速度。该方法实际是“标准位置”的仿真过程，最接近实车侧翻试验状态。但由于其具有计算时间长、效率低和对计算机硬件要求高且难于提取的缺点，不推荐采用。

方法二：借助ADAMS软件先仿真计算各位置的仿真初始角速度[9]，再用LS-DYNA软件进行仿真分析。该方法需要借助另外的软件，从实用性上不推荐作为首选措施。

方法三：在仿真求解前，先通过LS-DYNA软件中的刚柔转换功能进行预运算，得到第2、3侧翻位置车体的角速度，分别作为相应仿真初始位置的仿真模型的初始边界条件输入进行仿真分析。具体方法如下：客车从临界侧倾位置开始侧翻，在未接触地面前车体不产生变形，采用关键字*Deformable_to_Rigid_Automatic将车体设置为刚体[10]。由于刚体的积分计算效率高，可以在很短的时间内完成预运算，提取到各位置的角速度。同时通过刚柔转换计算得到的质量、能量、转动惯量都与车体质心和状态有关，和车体的仿真状态更吻合。因此，通过刚柔转换方式进行试运算得到的角速度更合理，且计算效率高得多。同时该改善措施仿真计算的连贯性、实用性都比较好。该方法实际是方法一的改进，推荐作为首选措施。

采用刚柔转换功能试运算得到的各位置的瞬时角速度(临界侧倾位置的初始角速度也设置为5°/s)及对比见表2。由表2可知，采用刚柔转换计算的各初始位置的角速度更接近仿真软件直接计算得到的角速度，其误差主要还是弹性体自身产生的摩擦能消耗而刚体不存在能量消耗导致，通常5%的误差范围可以接受。

表2 3种方法得到的不同位置的角速度 rad/s

将表2中由刚柔转换计算得到角速度作为第2、3侧翻仿真初始位置的边界条件输入进行求解。仿真得到的3个初始仿真位置的立柱变形量比较接近，其中最大误差为3.4%，在可接受的范围内；而加速度峰值的误差分别为4.5%和4.9%，也满足要求，其中第3侧翻仿真初始位置的质心加速度仿真曲线如图6所示。

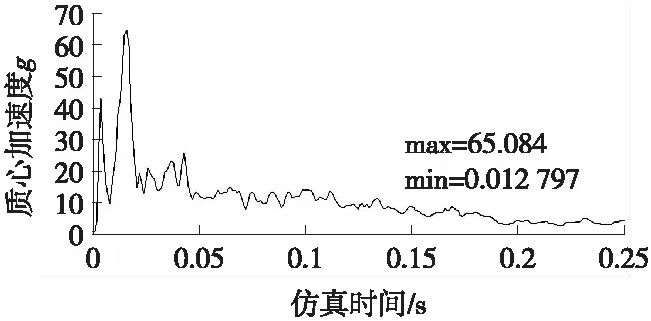
图6 第3侧翻位置质心加速度曲线

综上，采用改善后的初始角速度进行仿真得到的结果与“标准值”的误差大幅度降低，可以有效地提高仿真结果的可信度。

4 结束语

选取3个侧翻初始位置按常规方法进行仿真，结果表明：仿真初始位置选取对仿真结果影响较大，差别来自仿真输入的初始角速度的理论计算不合理。推荐采用LS-DYNA软件的刚柔转换功能，先预运算获得刚接触地面瞬间或中间某时刻的角速度值，再将该值作为初始边界条件输入进行仿真，其仿真结果更接近“标准值”, 仿真结果的可信度更高。