基于多阶局部度数峰值点的局部社区发现算法
王得翊, 焦澳琛, 陈音拿, 安静, 康琦, 汪镭
(1.同济大学 控制科学与工程系, 上海 201804;2.上海应用技术大学 电气与电子工程学院, 上海 201418)
0 引言
随着科学研究对象规模的不断扩大和结构的进一步复杂,针对复杂网络的研究已经成为生物学、社会学、经济管理学、流行病学、统计物理学等诸多学科前沿领域的研究热点之一[1]。复杂网络一般具有社区结构,即复杂网络往往可以被自然地分成一系列节点组,同一组的节点一般更具有相连相关的倾向[2]。社区发现能够检测复杂网络中的社区结构,是分析复杂网络、挖掘网络信息的有力方法,例如,通过研究蛋白质中氨基酸的连接关系发现功能模块和预测, 根据节点信息熵相似性和社区信息熵稳定性进行洗钱社区发现,因而自Kernighan-Lin算法[3]被完善并被用于图分割始,社区发现算法有了长足的发展。
传统的社区发现算法已知全局网络信息对网络中所有节点进行社区划分,分为非重叠社区发现算法和重叠社区发现算法。非重叠社区发现算法的结果中每个节点只能属于一个社区,例如,基于边介数的GN算法[4]、基于模块度概念FastUnfolding算法[5]和基于LeaderRank排序的标签传播算法[6]等。现实中复杂网络社区结构并非一个节点仅属于一个社区,例如,微博用户关注内容广泛难以被分入一个社区[7]。重叠社区发现算法可以允许节点同时属于多个社区,例如,基于完全子图的派系过滤算法[8]等。传统的社区发现算法需要事先知道全局网络的信息,网络规模巨大,不易获知全局网络信息。
局部算法[9]选择种子节点并以一定的方式扩张形成社区。在种子节点选取问题上,LFM算法[10]主张以随机选择的方式确定种子节点;基于图遍历的局部社区发现算法[11]将度数较低的节点作为种子节点;提出局部度数中心点的概念,主张以局部度数最高的节点作为种子节点[12],但由于种子节点选择标准严苛,算法不能较为全面地感知各个社区的关键节点,发现社区的稳定性略有欠缺。
本文的主要贡献:(1)在局部度数中心点的基础上,提出了多阶局部度数峰值点的概念,并将其作为种子节点的选择依据。(2)提出了基于多阶局部度数峰值点的种子节点选择方法和局部社区检测框架。
1 相关工作
1.1 局部社区扩张算法
Clauset[13]提出了衡量局部节点组社区结构显著度的标准,即局部模块度。算法从一个给定节点作为初始节点组开始,不断将节点组的邻居节点加入节点组并更新局部模块度,直到加入任何邻居节点都不能使模块度值增大,得到扩张的局部社区。
罗峰等[14]提出了基于模块度的扩张算法。先将能使子图模块度增大的相邻节点加入子图,再将子图中能使模块度值进一步增大的节点删去,直至任何节点的加入和删去都不能使子图的模块度值增大为止,得到扩张社区。
Bagrow等定义了与给定初始节点间最短路径等于L的节点集合L-shell[15]及其总出度KL。L-shell不断扩张,直至KL增长速度小于给定阈值α,扩张停止,L-shell已覆盖节点构成扩张社区。
1.2 局部度数中心点框架
对于网络G中的节点v,如果节点v的度数不小于它的任何一个邻居节点,则称节点v为“局部度数中心点”。从初始节点开始找到与初始节点最近的“局部度数中心点”,并以此为新的初始节点扩张得到局部社区。
2 基于多阶局部度数峰值点的局部社区发现算法
网络中度数最高的节点往往具有与其他节点紧密的联系,以它为关键节点进行扩张能达到较好的扩张社区效果,而一个社区内的关键节点度数可能不大。规模大、节点间联系紧密的社区内往往囊括了全网络大部分度数较高的节点,局部度数中心点是基于此建立的关键节点概念。
局部度数中心点框架下容易出现:某节点是其所在社区的关键节点,但与它的所有邻居节点相比,它并非度数最高的节点,这是因为度数高于它的节点属于其他的社区,如图1所示。

图1 局部度数中心点概念失效
图1中,有{1,7,8,9,10,11}和{2,3,4,5,6}两个社区,节点1和2分别是两个社区的关键节点。按照局部度数中心点的概念,节点2并非关键节点,这是因为它的邻居节点1的度数比它高,而节点1属于另外的社区。
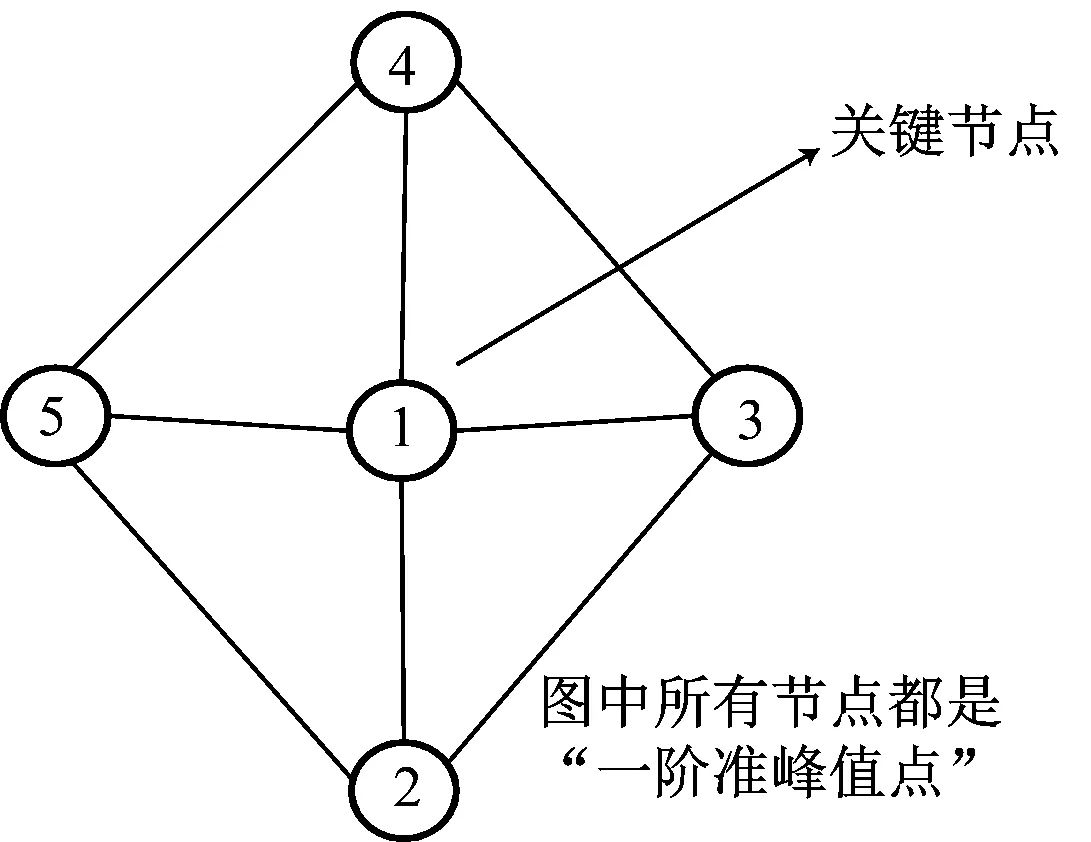
要避免上述情况,首先要放宽标准,即在寻找关键节点时,允许其邻居节点中有一些度数高于它,称这样的节点为准峰值点。
定义1:对于网络G中的节点v,如果节点v的邻居节点中有t个节点的度数高于它,则称节点v为“t阶准峰值点”。
一般地,处于同一社区内的节点间联系相对紧密,其内部的同阶准峰值点之间更有可能相互连接,不大可能成为社区的关键节点;相对孤立的准峰值点更有可能成为社区的关键节点,如图2所示。

(a)
(b)
据此给出关键节点的定义。
定义2:对于网络G中的节点v,如果节点v是“t阶准峰值点”,且它的邻居节点中没有其他“t阶准峰值点”,则称节点v为“t阶局部度数峰值点”。
算法从给定节点出发,不断检测邻居节点,直到发现第一个符合要求的多阶局部度数中心点,则以该节点为种子节点,按照既定方法扩张得到局部社区。若发现多个符合要求的节点,则任意选取一个阶数最低的作为种子节点。
给定一个阶数灵敏度系数T,只有被发现的峰值点的阶数不大于T才称为找到种子节点。一般地,灵敏度系数越小,算法精确度越高,但稳定性越低。
3 实验分析
采用LFR基准网络数据集[16]作为研究对象。LFR基准网络生成后节点的社区分布已知,故使用F值作为对给定节点社区划分效果评价指标。
3.1 峰值点阶数灵敏度系数T的选定
网络的规模越大,各节点的度数普遍越高,LFR基准网络的混合参数μ越大,对应现实中网络的社区越不明显,探究不同网络规模与不同混合参数对灵敏度系数的要求是很有必要的。
(1) 网络规模与灵敏度T的关系
固定LFR社区的混合参数为μ=0.1,生成社区规模为1 000、2 000、3 000个节点的三个网络。网络参数如表1所示。

表1 网络规模与灵敏度T关系实验参数
灵敏度系数由0开始逐渐增长,建立全局社区划分精确度-灵敏度系数关系,如图3所示。

图3 不同规模网络全局社区划分精确度与峰值点阶数灵敏度系数的关系
在网络规模相同的情况下,加入多阶局部度数峰值点较之只有局部度数中心点的情况,划分精度得到了明显改善,选取的灵敏度系数T越大,划分精度越高。
(2) 网络混合参数与灵敏度T的关系
将LFR社区的社区规模固定在1 000个节点,生成混合参数为μ=0.1、0.2、…、0.5的五个网络。网络具体参数如表2所示。

表2 网络混合参数与灵敏度T关系实验参数
对于不同的灵敏度建立全局社区划分精确度-灵敏度系数关系,如图4所示。
混合参数越大,社区结构越不明显的网络,其社区划分的精准度越低。随着灵敏度系数的提高,不同混合参数的网络之间的差异并未被消除。网络混合参数相较于规模对社区划分质量影响更大。
3.2 算法分析
为说明本算法框架的优势,将其与局部度数中心点框架进行对比实验。实验网络具体参数如表3所示。

表3 对比实验网络参数
对网络中的每个节点运行算法,并将所得局部社区与真实社区进行对比,得到节点在指定算法下的F值。F-节点关系如图5所示。

(a) LMD

三种扩张算法在两种框架下的F值对比如表4所示。

表4 两种框架下各节点F值平均值对比
由表4可知,基于多阶峰值点选取种子节点的算法效果较之局部度数中心点有明显的提高。
4 总结
本文基于社区内关键节点度数较高和关键节点间联系松散对社区结构的认识,提出了多阶局部度数峰值点的概念及社区发现算法,精确度更高,稳定性更强。在一定范围内,选取的阶数灵敏度系数越大,算法精确度越高。然而,随着阶数的增大,其峰值特性逐渐弱化,带动算法精确度提高的边际效益递减,不稳定性增加。当阶数足够大时,算法退化为以既定节点为扩张初始节点的普通算法。
本文为解决局部社区发现种子节点选取问题,提供了寻找多阶局部度数峰值点的框架。以多阶局部度数峰值点为种子节点进行扩张能在一定程度上改善原局部扩张算法的性能。该算法无须得知全局网络的信息,仅通过初始给定节点便能自主探索网络,有着较低的计算复杂度,有助于复杂网络局部结构的研究。在同一网络中研究多个节点的社区归属时,本算法不限制各节点归属社区的数量,有助于探索复杂网络中的重叠社区。

