气象因素对城市公路交通通勤效率的影响研究
夏丹妮, 余蜀豫, 许伟, 白莹莹, 覃彬全
(1.重庆农村商业银行, 重庆 401120;2.重庆市雷电灾害鉴定与防御工程技术研究中心, 重庆 401147;3.重庆市气候中心, 重庆 401147;4.重庆市气象安全技术中心, 重庆 401147)
0 引言
气象因素是对城市交通系统影响最大且最频繁的因素之一,这些影响包括对交通设施的影响,对交通工具运行状态的影响,对交通工具运行效率的影响等[1]。城市交通工具,包含公路交通、轨道交通、水运交通等,对气象因素敏感程度不同,比如轨道交通对雷电的敏感程度很高,雷电电磁脉冲甚至会导致地铁非计划停运。气象因素对城市交通的影响集中体现在交通事故或者交通故障上。目前,大多数研究集中在不同气象因素对交通安全的影响机理以及如何防御交通气象灾害等方向上[2-4]。
对大部分人而言,工作日的通勤通常是日复一日地沿着相同的路径进行,气象因素不仅可以直接影响通勤交通工具的运行效率,而且可以影响人们的通勤习惯和偏好从而间接影响交通效率。本文从公路交通通勤时间出发,分析温度、湿度、风速、天气状况、舒适度等气象因素对同一通勤路段的影响,探寻气象因素对交通效率的影响程度,进而为提升城市交通效率和提高道路流动性提供技术支撑。
1 数据来源
通勤数据来源于2016—2018年连续记录,固定A点到B点同一通勤路径且距离为7.1公里城市道路的早高峰通行时长(出发时间保持在同一时间段),气象因素来源于该区域同时段的实时监测数据,包含温度、湿度、风速、天气状况四大主要气象数据以及一个人体舒适度指标——修正人体舒适度指数(Kssd)[5],该指数表征人体在大气环境中舒适与否,属于人体对环境气象感觉的定量化指标,能更加直观地评价大气环境对人体的影响。气象和通勤特征数据统计如表1所示。
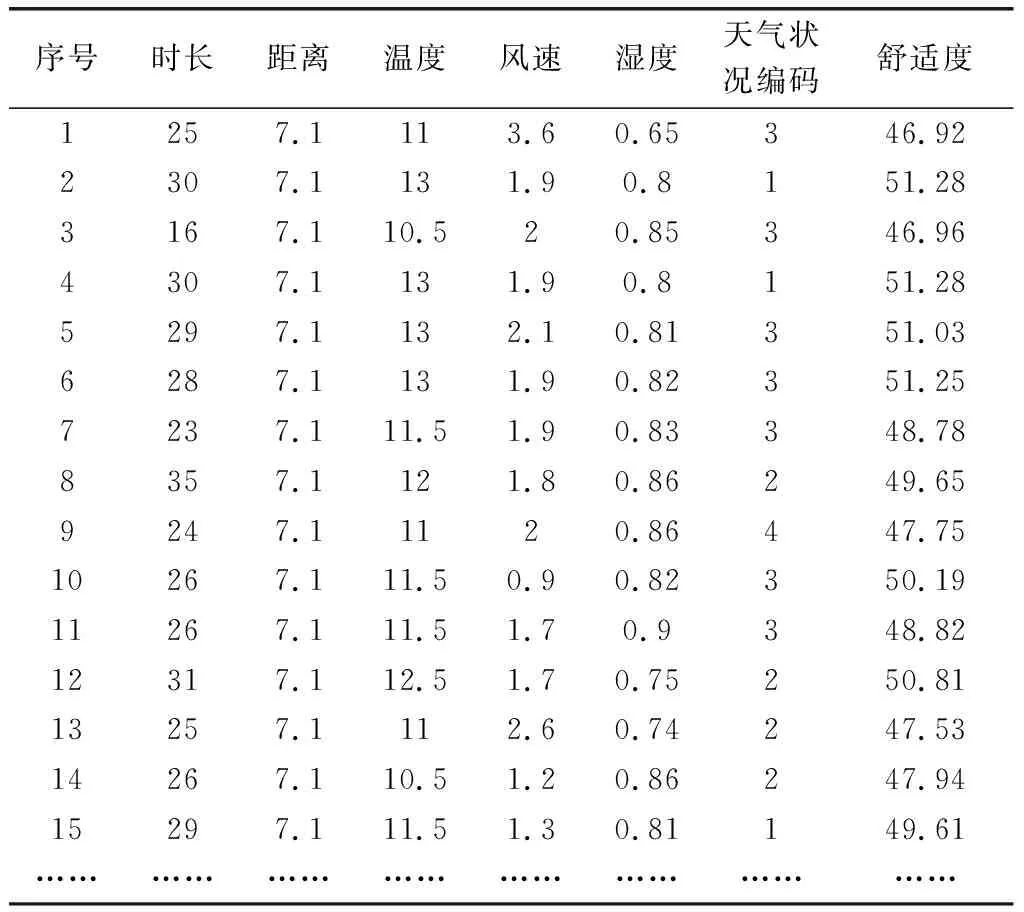
表1 气象和通勤特征数据统计表
因为恶劣天气一直是影响道路交通安全的主要因素,表1根据天气状况的类型进行编码,数字从小到大分别为晴、多云、阴天、阵雨、小雨等,数字越大代表天气状况越恶劣。
2 灰色关联分析
灰色关联分析法是一种定性与定量相结合的方法,基本思想是用点在纵轴上的接近程度来描绘因素间的关联度,两条曲线的形状越相似,他们的关联度就越大[6]。由于其对样本量的低要求以及在短期预测中所表现出来的准确性,使其具有广泛的实用性。但实际应用中,灰色关联分析仍有一些局限性,这时就需要与实际相结合[7],多计算几种灰色关联度综合评判。本文采用邓氏灰色关联分析法和灰色相对关联度分析法,对五种气象因素与通勤时间的相互影响关系进行定性比较。
设早高峰通行时长X0=(x0(1),x0(1),…,x0(n))为系统特征行为序列,且温度、湿度、风速、天气状况和人体舒适度分别为:
X1=(x1(1),x1(1),…,x1(n))
X2=(x2(1),x2(1),…,x2(n))
X3=(x3(1),x3(1),…,x3(n))
X4=(x4(1),x4(1),…,x4(n))
X5=(x5(1),x5(1),…,x5(n))
2.1 邓氏灰色关联度
按照灰色关联公理[8],邓氏灰色关联度计算分五步进行。
第一步,求各序列的初值象(或均值象),如式(1)。
(1)
第二步,求X0与Xi的初值象对应分量之差的绝对值序列,如式(2)。
(2)
第三步,求绝对值序列中的最大值与最小值,分别记为:
第四步,计算关联系数,如式(3)。
(3)
第五步,计算关联度,如式(4)。
(4)
带入公式计算,温度、湿度、风速、天气状况、人体舒适度与早高峰通行时间的邓氏灰色关联度,结果如表2所示。

表2 五种气象因素与早高峰通勤时长的邓氏灰色关联度
由表2可知,人体舒适度与早高峰通行时长的关联度最大,其次是温度,天气状况关联度最小。
2.2 灰色相对关联度
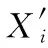

(5)
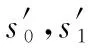
(6)
(7)
(8)
带入公式计算,温度、湿度、风速、天气状况、人体舒适度与早高峰通行时间的灰色相对关联度,结果如表3所示。

表3 五种气象因素与早高峰通勤时长的相对灰色关联度
由表3可知,人体舒适度与早高峰通行时长的关联度最大,其次是温度,这两个因素相较于其他三个因素来说,关联度明显高出很多。
2.3 灰色关联分析结论
灰色关联分析法的核心是对比两条曲线的相似程度,两条曲线的形状越相似,他们的关联度就越大,邓氏灰色关联度更多是从绝对量的关系着眼考虑,相对灰色关联度更多是从变化速率着眼考虑。综合来说,人体舒适度和温度是五种气象因素中与早高峰通行时长关联度最大的两个因子。通常情况下,恶劣天气是影响交通安全的主要因素,通过灰色关联分析发现,天气状况与早高峰通勤效率的相关性很低,说明通勤交通不同于传统的货运、客运交通,天气的恶劣程度对早高峰出行的影响不大,反而是温度和人体舒适度更能影响早高峰的通勤时长。
3 相关系数分析
事物之间的统计关系普遍存在,却不像函数关系那样直接,绘制散点图和计算相关系数是相关分析最常用的工具[9]。散点图能够直观展现变量之间的统计关系,但不够精确。这里采用最常用的相关系数——Pearson皮尔逊相关系数,也称为皮尔逊积距相关系数,它是对两个连续型随机变量之间线性关系的标准化测量,如式(9)。
(9)
式中,n表示样本量;xi和yi分别表示两个变量的值。
利用Pearson皮尔逊相关系数进行变量间线性分析通常有两步。
第一步,计算样本相关系数r。
第二步,对样本来自的两总体是否存在显著的线性关系进行推断。
将温度、湿度、风速、天气状况、人体舒适度、早高峰通行时间数据按照上述步骤和公式进行处理计算后,Pearson相关性计算结果的数值如表4所示。

表4 五种气象因素与早高峰通勤时长的相关性
由表4可知,湿度、人体舒适度与早高峰通行时间有着显著线性关系,风速与早高峰通行时间无显著线性关系。湿度的相关系数r2=|0.021|<0.3,天气状况的相关系数r4=|-0.143|<0.3,说明湿度、天气状况与早高峰通行时间之间的线性相关关系较弱。温度的相关系数r1=|0.795|≈0.8,人体舒适度的相关系数r5=|0.799|≈0.8,说明温度、人体舒适度这两个指标与早高峰通行时间之间具有高度线性相关关系,且是正相关。相关系数分析结果表明温度和人体舒适度是影响早高峰通勤时长的重要因素,温度越低,通勤时间更短。同时,天气状况的恶劣程度对通勤时间的影响程度很低,进一步说明恶劣天气并不是影响通勤效率的主要因素,这点和传统交通有所差别。
4 回归分析
通过上面的计算和分析,可以看出温度、人体舒适度与早高峰通行时长之间有着很高的关联度和线性相关性,接下来通过回归方程的形式来描述和反映这种关系。因为修正人体舒适度指数是综合多项气象因素计算出的二级气象服务产品,包含风速这个与早高峰通行时间无显著线性关系的因素,所以这里只针对温度进行线性回归分析。同时,为了更加直观地展现温度对城市公路交通通勤效率的影响,用早高峰该路段的通勤平均速度进行分析,即平均速度=距离/早高峰通行时长。
利用样本数据获得回归线通常可以采取函数拟合的方式,根据一定的统计拟合准则[10],对模型的各个参数进行估计,这里采用最小二乘法作为统计拟合准则。设平均速度为因变量,温度为自变量,首先进行线性回归分析,通过计算后,温度与速度的回归线性函数如式(10)。
v=17.687-0.316T
(10)
通过回归方程的统计检验,均满足相关要求,式(10)在一定情况下可以反映该城市路段温度对通勤速度的影响。
接下来,通过曲线拟合进一步分析样本数据中温度和通勤速度的相关性,通过多种曲线模型拟合后发现,幂函数更能表征样本数据,通过残差分析排除异常值后拟合曲线,如图1所示。

图1 多种函数的拟合曲线
回归幂函数如式(11)。
v=36×T-0.4
(11)
分别计算幂函数和线性函数的拟合优度,幂函数的拟合优度高于线性函数,说明式(11)能更好地描述温度和通勤效率的关系。可以看出,温度和通勤速度间有较为显著的负相关关系,温度越低,早高峰通勤速度越快,通勤时间越短;反之温度越高,早高峰通勤速度越慢,通勤时间越长。
5 总结
(1) 同一个行为人群中的个体具有相似的习惯,也具有相似的生活方式和相似的职业路径[11],比如旅游出行的时间、交通工具的选择、出行的目的地,相同行为人群有着高度的一致性。重庆市区交通路线集中度很高,非市区核心道路占绝大部分比例,仅利用某一时刻的通行速度进行分析,不能很好地反映通勤这个行为特征,也不能很好地分析气象因素对城市通勤效率的影响。从上面分析可以看出,影响交通安全的主要气象因素——天气状况与通勤效率的相关性很低,说明与广义的交通运输不同,城市通勤交通受恶劣气象的影响程度低,气象因素只是影响了人们的行为习惯或者偏好,从而在出行的数量、交通选择、出行集中度等方面间接影响了市区通勤效率,最终表明温度越低,早高峰通勤效率越高。
(2) 对回归函数DW检验,结果发现回归函数存在一定自相关,说明回归函数的拟合还需要进一步提高,说明仍有一些潜在规律没有反映出来。未来如果利用导航软件的大数据平台,结合市区更大范围的实时数据,可以进一步研究气象因素与交通效率之间的相关性,从而更加深入地研究气象与行为习惯之间的影响关系。

