轨道牵引电机铁心材料参数识别

任晓辉，杜小渊

(中车永济电机有限公司，陕西 西安 710016)

随着轨道交通车辆向高速、重载方向发展，对产品可靠性、舒适性要求愈加严格。振动与噪声作为电机重要性能指标，日益成为用户关注重点。开展电机振动、噪声相关因素的分析、研究和控制具有重要的意义。铁心是电机电磁振动的传递媒介，电磁激振力通过铁心传递到机座，其振动变形引起的电磁噪声是电机噪声主要来源,铁心振动参数识别对电机性能的改善有着重要作用。现阶段已有不少对电机铁心研究的论文。王天煜等[1]研究了叠片结构以及绕组质量和刚度对固频的影响。LONG 等[2]指出，轴向弹性模量Ez对于面内挠曲振动影响不大，但由于叠压铁心的层叠效应，以及叠压铁心中间柔性绝缘材料作用，使得叠压铁心的轴向弹性模量比硅钢片的弹性模量小很多，Ez低于其径向弹性模量Ex(Ey)。吴署明[3]指出，加强铁心的轴向刚度，可以降低振动和噪声。吴胜男[4]指出，铁心叠压系数低会使结构相对松散，刚度降低，对电机振动噪声产生影响，杨氏模量越大，电机电磁振动噪声越小。这些文献均对铁心参数的重要度及影响开展了讨论分析，但对如何识别振动参数未展开深入分析。为探究叠压力和铁心轴向长度对铁心材料参数影响，确定电机铁心横观各向同性材料参数，本文以某高速异步牵引电机定子铁心为研究对象，基于ANSYS 参数化分析横观各向同性材料参数对铁心相应振型及其频率影响，通过模态试验与响应面仿真计算的分组优化修正，获取叠压铁心横观各向同性材料参数，掌握牵引电机铁心横观各向同性参数敏感度，为仿真提供准确铁心参数。

1 铁心结构特征

铁心是由厚度1 mm 以下的电工钢板(硅钢片)沿轴向叠压而成，并不是连续弹性体(见图1)。以叠压方向为Z向，硅钢片在XOY面内，则该平面内材料具有各向同性的性质，而沿铁心轴向(Z轴)的材料特性与XOY面内的材料特性有差异。因此可认为铁心具有横观各向同性材料的特性。

图1 定子铁心有限元模型与实物Fig.1 Stator core model and physical picture

由弹性力学可知：各向同性材料具有3个独立的材料参数，正交各向同性材料有9个独立材料参数，而横观各向同性体材料具有5个独立的材料参数，其材料参数关系为：

泊松比，υxy=Ex/2Gxy-1，υxz=υyx；

杨氏模量，Ex=Ey，Ez；

切变模量，Gxz=Gyz，Gxy.

由于通常泊松比变化非常小，故忽略泊松比的改变，假设各方向泊松比均为硅钢片的泊松比。因此，本文将主要针对铁心结构4个独立的材料参数进行识别。

铁心振型特征方面，通过开展铁心自由模态分析，以轴向长度270 mm 铁心为基础模型，参数取值依据硅钢片属性。通过仿真，得到的铁心模型振型大致分为4 类。如图2 所示。定子模态按空间节点数的顺序定义，其中节点是指模态振型值为零的位置，以mode(n,m)来描述模态的阶次，n为周向节点数，表示圆周上一共有n个完整的正弦波形，m为轴向节点数。

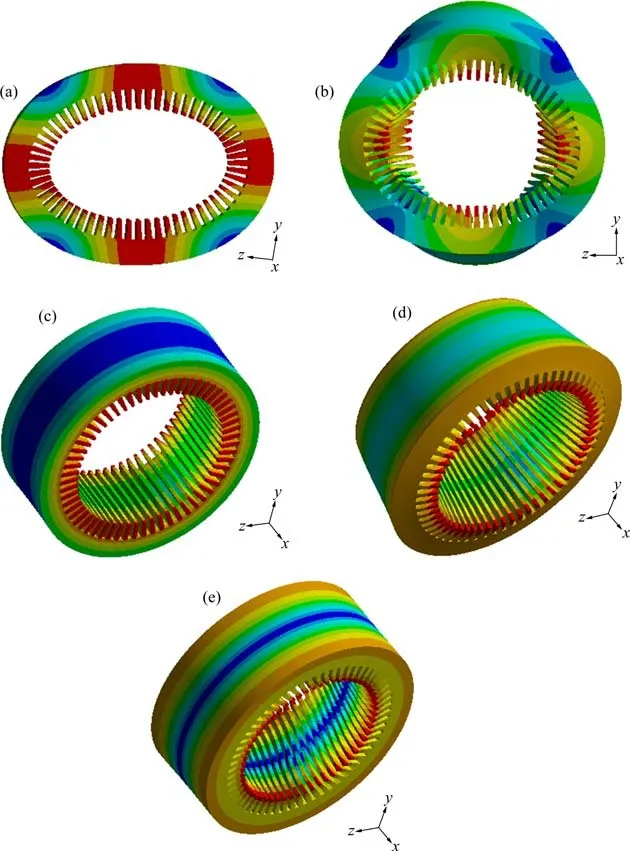
图2 仿真模态振型Fig.2 Simulation mode shape

对称振型的m为0，表示2 个端口的振动是同相的；

反对称振型m为1，则2 个端口的振动是反相的。

收缩扩张振型分为2 种，一种为同相收缩扩张，另一种为反相收缩扩张。

扭转振型，2个端面的转动方向相反。

2 材料参数敏感度分析

利用基于相对灵敏度分析的参数选择方法，开展模态分析。以定子铁心模型为例，通过参数化分析方法，在一定范围修正Ex,Ez,Gxy和Gxz的值，研究不同类型模态振型对应频率的变化趋势和灵敏度。材料参数的设置采用控制变量法，赋各向异性材料参数来反映层叠效应，参数基础取值依据硅钢片属性，开展单一参数驱动数值模态分析。

为直观识别特定振型频率随参数变化规律，针对Ex，Gxz，Gxy和Ez的仿真结果，从每一类振型中选取一个作为代表，选择n=4对称、反对称模态以及反相收缩扩张和扭转模态，做出折线图如图3所示。

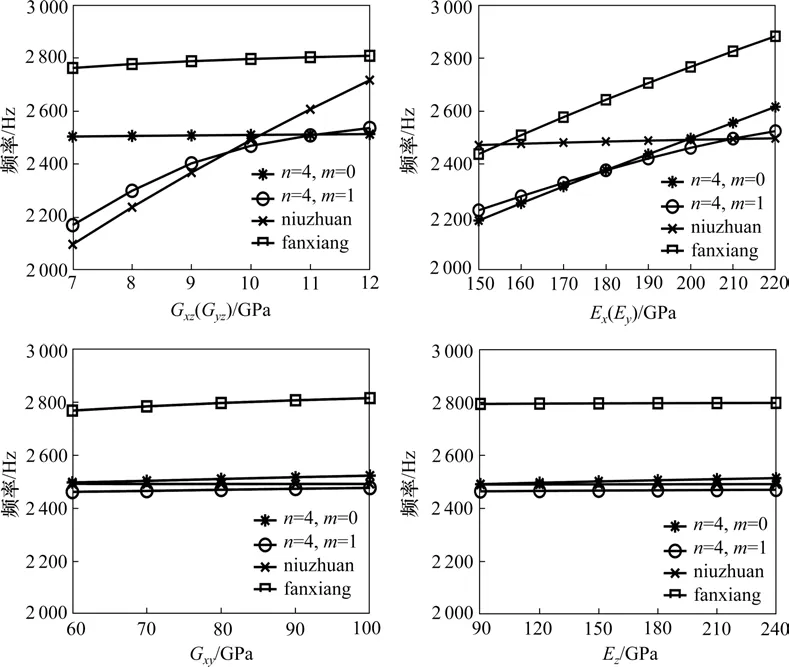
图3 仿真结果折线图Fig.3 Line chart of simulation results

由仿真结果的频率折线图，可以得出以下结论：

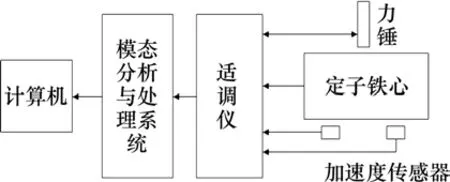
图4 铁心模态实验测试系统Fig.4 Core modal test system

Ex的变化对扭转振型几乎无影响，对称振型与收缩扩张振型的频率变化速率基本一致，比反对称振型更为敏感。

Gxz的变化对反对称振型和扭转振型的频率产生明显影响，而且相对其他参数的影响，变化速率很大。

Gxy的变化对除扭转振型外其他所有振型的频率产生一定影响，但是相较Ex和Gxz，其影响程度很小，变化不明显。

Ez的变化对所有振型的频率影响都非常小，从表中可以看到，Ez从90 GPa升高到240 GPa，除n=5 的对称模态频率变化略大于1%，其余各模态的频率变化均小于1%。

3 模态实验及材料参数辨识

3.1 模态实验

结合模态分析相关基础理论，选择利用移动力锤、固定传感器的锤击法对定子铁心进行自由悬挂状态下的模态特性测试。

进行多参考点锤击测试技术(MRIT)，移动力锤遍历所有测点对其测量，如图5所示。

图5 铁心实验测点Fig.5 Test points model of stator core

基于电机定子铁心所有测点得到的全部FRF数据，利用稳态图确定其系统极点。稳态图计算过程中，按照工程的实际需求，关注铁心的低阶模态特性，分析带宽设置为0～3 200 Hz。采用Time MDOF 模块进行数据分析处理，加速度传感器测量得到的平均FRF 曲线识别出主要模态参数。

图6 某型铁心模态频率及振型Fig.6 Modal frequency and model diagram of a certain type stator core test

3.2 材料参数辨识方法及结果

由于电磁激励沿轴向分布一致，铁心对称振型的模态参与因子远大于反对称模态。以对称模态的试验结果为主要目标进行参数识别，试验得到的各阶模态频率作为优化目标，修正定子铁心等效模型的Ex，Gxy值，接着修正Gxz，使反对称模态的仿真结果逼近试验结果，最终获取定子铁心的横观各向同性材料参数。

定子铁心的横观各向同性体现在模态特性上，主要表现为两端口振动同相位的对称模态和振动反相位的反对称模态。

对称模态的振型主要源于XOY面内的拉伸、压缩和剪切，拉伸和压缩取决于该平面内的杨氏模量Ex，剪切取决于切变模量Gxy，对称模态主要受Ex和Gxy这2个参数的影响。

反对称模态振型可看成对称模态的径向振型沿轴向的叠加，Ex和Gxy亦会影响反对称模态频率。铁心在YOZ 和ZOX平面受到剪切力也会产生这种反对称模态的振动，这2个平面内的剪切形变取决于平面内的切变模量Gxz和Gyz，反对称模态主要受Ex，Gxy和Gxz这3个参数的影响。

应用ANSYS 中的DesignXplorer 多目标快速优化模块开展分析，采用基于实验设计(DOE)方法获取铁心横观各向同性材料参数，具体为中心复合设计法(CCD)，响应面算法为完全二阶多项式法，优化方法为Screening方法。

有限元仿真中，因无法直接设置横观各向同性材料，设置中通过添加正交各向异性材料，建立对应横观同性约束，实现将材料表现为横观各向同性。以前文中待确定的4项材料参数为优化变量，特定模态频率值为优化目标，使用响应面技术来插值结果，实现优化分析。

以n=3，m=0 对称模态的频率为例，生成响应面，如图7所示，可以看出，该响应面很平滑，频率随Ex和Gxy的增大而增大，且对Ex的变化更为敏感。

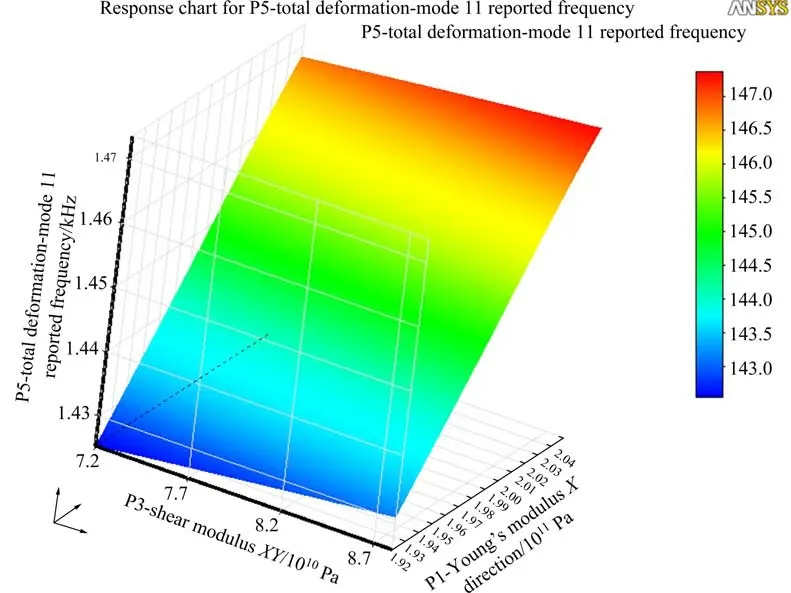
图7 n=3，m=0模态频率响应面Fig.7 Modal frequency response surface with n=3,m=0

依据图8开展定子铁心参数的试验对比分析。

图8 定子铁心模态特性测试流程图Fig.8 Flow chart of stator core modal characteristic test

获得的铁心参数如表1 所示，材料密度ρ/(kg∙m−3)为现场称重与CAD 模型体积之比得到，其余参数修正得到。

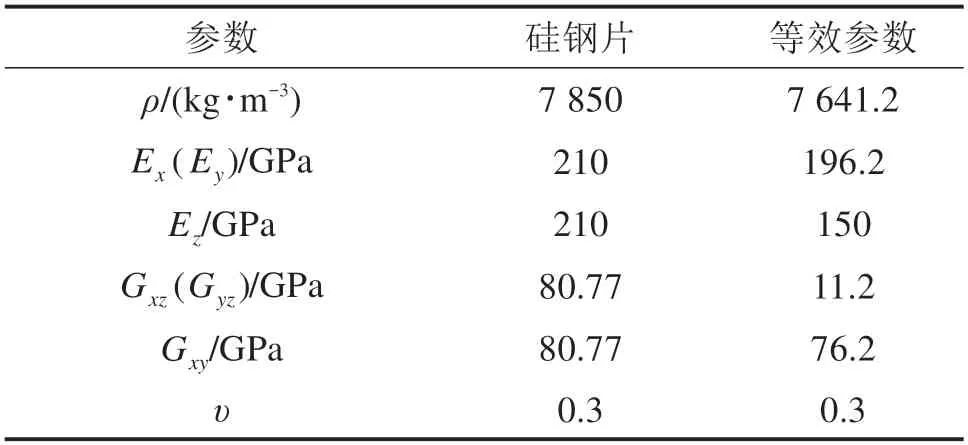
表1 铁心材料参数Table 1 Stator core material parameters

使用该组铁心参数进行模态仿真，得到的模态振型和频率与实验对比如表2所示。

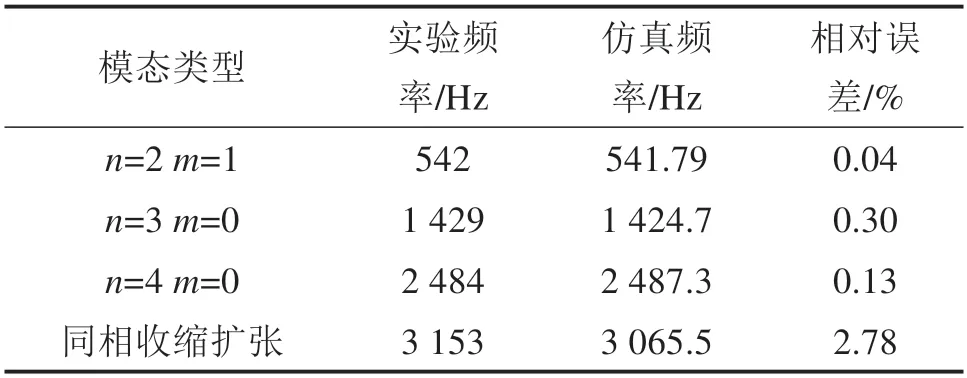
表2 模态频率对比Table 2 Modal frequency comparison

以上对比得出，仿真获得铁心的各个模态振型与实验一致，仿真频率与实验频率误差很小，同相收缩扩张模态频率误差小于3%，其余各个模态频率的误差小于1%。

4 铁心长度、叠压力对模态影响分析

铁心长度是电机设计中核心的电磁参数，叠压力则是电机制造过程中的重要工艺参数。为识别2 种参数对铁心振动特性影响，根据铁心结构，综合制定试验方案，开展多工况铁心模态特性测试。

铁心模态实验总共选取了12 个不同工况，选取3 个不同轴向长度，每个轴向长度使用了4 种叠压力加压。叠压铁心具体参数如表3所示。

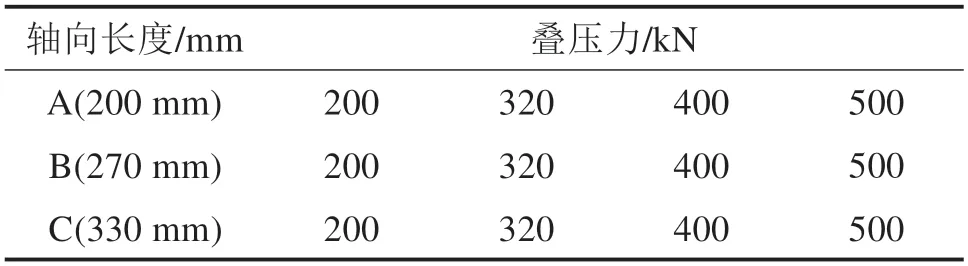
表3 铁心测试工况Table 3 Staror core test conditions

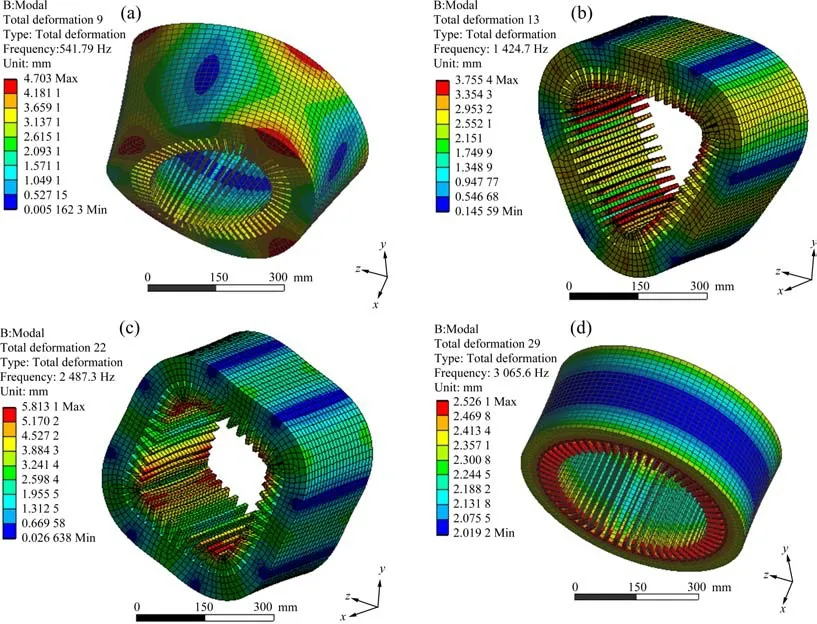
图9 铁心仿真振型及频率Fig.9 Stator core simulation mode and frequency

同前述实验模态参数获取方法，识别出各工况铁心模态参数并对参数进行汇总。

为了更直观地观察叠压力对模态频率的影响，以各铁心模型一阶实验值为代表，分别取各型号一阶模态频率绘制折线图，如图10所示。

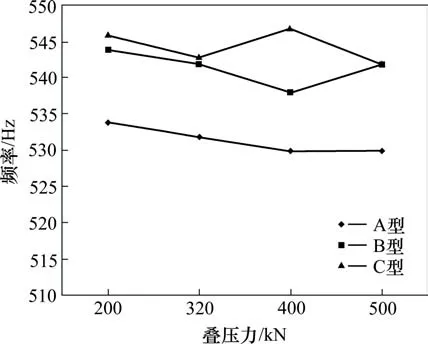
图10 各型铁心模态1阶频率随叠压力变化Fig.10 Variation of the first-order modal frequency of various stator cores with pressure

铁心长度影响下，随着轴向尺寸增加，除B型(270 mm)铁心在叠压力500 kN 时、C 型(330 mm)铁心在叠压力400 kN 条件下数值变化，各型铁心不同叠压力条件下一阶频率基本呈明显上升趋势。说明随长度增加，铁心结构呈“钢化”效应；

在叠压工艺范畴内开展叠压力影响分析，随叠压力增加，A 型(200 mm)铁心频率呈下降趋势，B 型(270 mm)、C 型(330 mm)铁心亦基本呈下降趋势。说明随叠压力增加，铁心结构呈“软化”效应。

对铁心其余阶次进行分析，亦具有相同变化趋势。

综上所述，可以得出以下结论：

1) 同一叠压力铁心在不同轴向长度下，各个模态频率的变化均小于2%，同时伴随长度增加，铁心频率增加呈“钢化”效应。

2) 同一轴向长度铁心在不同叠压力下，各个模态频率发生的变化均小于1%，说明现有实验叠压力范畴内，叠压力对铁心振动特性影响很小，但随着叠压力增加，铁心频率减小呈“软化”效应。

3) 通过现场技术人员测量得到的叠压系数，在轴向尺寸和叠压力的给定变化范围内，只有微小的差异。叠压系数可能对各向异性参数的影响更大。

表4 试验模态结果Table 4 Test modal results

5 结论

1) 明确铁心各个材料参数对模态频率影响程度的不同，使用参数化分析，确定了影响模态频率的主要材料参数。Ex和Gxy主要影响对称振型和收缩扩张振型，Gyz主要影响反对称振型和扭转振型，Ez对铁心模态频率影响不大。

2) 根据实验结果的部分模态频率，结合有限元仿真，成功获得各个轴向长度铁心的材料参数，并使用该参数进行有限元仿真，和其他模态的频率及振型吻合很好，验证了该方法的有效性和准确性。

3)选取不同轴向长度铁心、不同叠压力参数、共计12 种不同工况的铁心进行实验，通过结果对比，确定了轴向长度和叠压力对铁心模态特性的影响情况。