中国主要沿海港口效率及其收敛性研究

吴遵杰，巫南杰

(深圳大学 经济学院，广东 深圳 518060)

港口在一个国家对外贸易中发挥着重要作用。据中国海关总署和联合国贸发会议发布的数据显示，2017年中国进出口货运总量的约90%都是利用海洋运输，海洋货物运输量占据了全球货物贸易总量的80%以上。港口是海洋运输的重要基础设施，提高港口效率有助于促进中国对外贸易发展。因各港口所处地理位置、自然条件和腹地经济发展水平等方面存在差异，导致中国不同港口的效率存在差别。由于中国的港口主要集中在沿海地区，因此，研究中国主要沿海港口效率及其收敛性对于促进中国对外贸易发展有着重要意义。

中外学者已利用数据包络分析(DEA)方法对港口效率进行了研究。Diaz-Hernandez等[1]运用DEA和Malmquist指数方法研究西班牙19个港口货物装卸效率，发现低效率港口总体上有所减少，但港口仍存在着劳动力过度使用和装卸效率低下的问题；Wanke[2]使用两阶段网络DEA模型分析了促进巴西港口效率提升的主要因素，发现市场经济体制和港口的腹地经济效应对港口效率的提升有着积极作用；Cullinane和Wang[3]采用DEA方法测算欧洲69个主要集装箱码头效率，发现集装箱码头的年吞吐量、生产规模和地理位置等因素将影响港口效率；Suarez-Aleman等[4]采用随机前沿分析(SFA)方法研究2000—2010年70个主要发展中国家集装箱港口经营绩效，结果表明，私营部门的加入、多式联运的运用和公共事业部门的清廉等关键性因素提高了发展中国家港口经营效率。国内也有学者对中国港口效率进行了研究。王瑛等[5]运用数据包络分析(DEA)方法，研究中国1996—2010年物流业效率，发现提升物流从业员工素质、提高物流产业技术和发挥规模经济效应能促进物流业效率的提升；王玲和孟辉[6]对中国14个内河港口和17个沿海港口的效率进行了测算，发现货物吞吐量不足是制约港口效率增长的主要因素，且内河港口效率远低于沿海港口。

中外学者对港口效率进行了广泛研究，但仍存在以下不足：①国内学者的研究主要采用传统数据包络分析方法测算中国港口效率，而鲜有文献采用超效率数据包络分析方法研究中国港口效率。由于超效率数据包络分析弥补了传统数据包络分析对于效率评价值为1的有效单元无法继续进行评价的不足，并且可以在数据包络分析无效单元评价值保持不变的情形下，将数据包络分析有效单元进行依次排序，因此，有必要采用超效率数据包络分析方法测算中国的港口效率。②研究中国港口效率的收敛性的文献还很缺乏，分析中国港口的收敛性对于促进港口均衡发展有重要意义。基于此，运用2005—2016年中国20个主要沿海港口的面板数据，采用超效率数据包络分析(SE-DEA)方法测算中国各主要沿海港口效率，在此基础上，研究中国主要沿海港口效率的收敛性。

1 主要沿海港口效率测算

1.1 港口效率测算方法

Andersen和Petersen[7]提出超效率DEA模型，其核心思想为：在测算第j0个DMU(decision making unit，相似决策单元)的超效值时，首先将其从现有的评估体系中剔除，并用其他DMU投入产出的线性组合来表示，在此条件下求解能使得港口j0仍为DEA有效的投入要素径向扩张量，则该径向扩张量即为超效率值。对于一个拥有r种投入X(X1，X2，…，Xr)，m种产出Y(Y1，Y2，…，Ym)，n个DMU的生产系统而言，用于评价DMUi超效率值的线性规划模型为

(1)

1.2 港口效率评价指标体系

已有文献在港口投入与产出指标选取上主要分为生产法和间接法两种[8]。其中，生产法是采用资本、土地和劳动等生产要素作为港口投入指标，以装卸船桥吊或其他吊车数量、生产用泊位数、生产用万吨级泊位数和非生产用泊位数作为资本投入指标，以港口仓库和集装箱堆场面积作为土地投入指标，以港口在岗聘任制员工数量作为劳动投入指标。在港口产出指标方面，以货物吞吐量、集装箱吞吐量和旅客吞吐量作为产出指标。间接法则是采用港口企业的相关财务数据作为投入产出指标，以固定资产投资、流通股股数(股票总价值)、员工人数、主营业务成本等财务指标作为投入指标，以净利润、主营业务收入、每股净收益和盈余利润等指标作为产出指标。生产法与间接法的港口投入产出指标见表1。

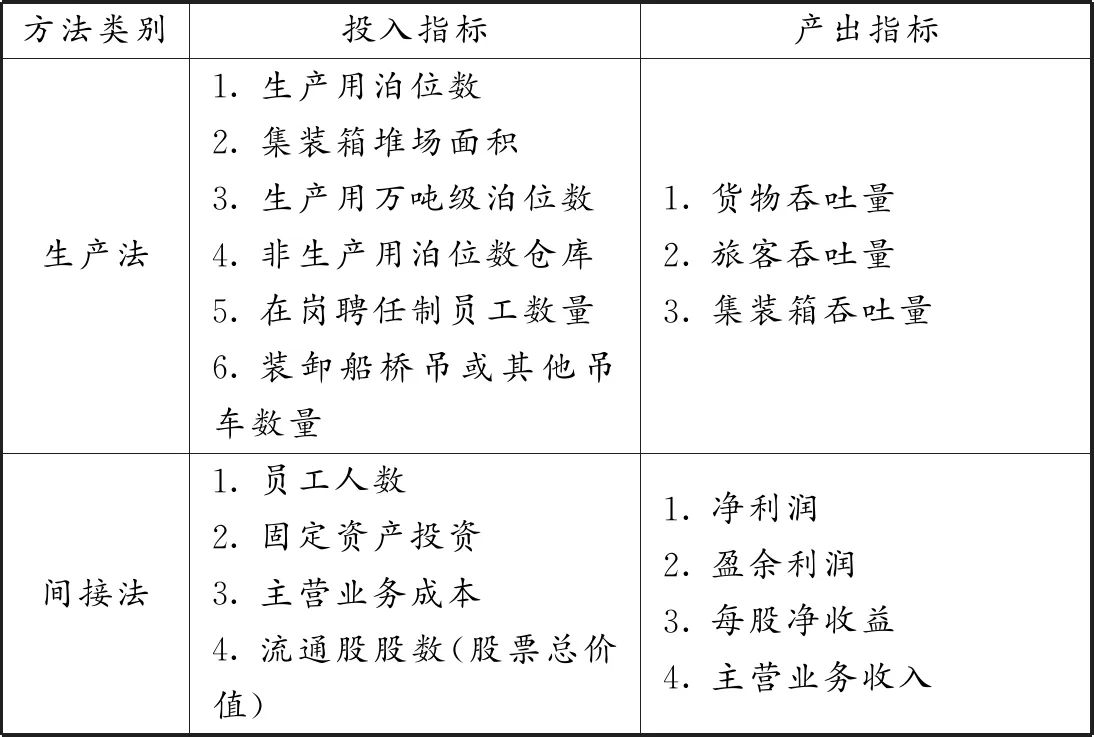
表1 生产法与间接法的港口投入产出指标

本文借鉴朱鹏颐等[9]以生产法来构建港口评价指标体系，以装卸船桥吊或其他吊车数量、生产用泊位数、生产用万吨级泊位数和非生产用泊位数作为资本投入指标，用生产用码头长度和非生产用码头长度作为土地投入指标，以港口在岗聘任制员工数量作为劳动投入指标，以货物吞吐量、集装箱吞吐量和旅客吞吐量作为产出指标，对港口评价指标体系进行构建，见表2。

表2 主要沿海港口效率评价指标体系

1.3 样本选取及数据说明

2016年，全国规模以上沿海港口完成货物吞吐量810 652万t，其中厦门港、深圳港、福州港、泉州港、温州港、宁波-舟山港、上海港、天津港、广州港、青岛港、大连港、秦皇岛、营口港、烟台港、日照港、连云港、汕头港、湛江港、海口港和防城港这20个主要沿海港口完成货物吞吐量595 307万t，占全国规模以上沿海港口总量的73.43%。为了客观真实地评价中国当前沿海港口效率及收敛性，选取厦门港、深圳港和宁波-舟山港等20个具有代表性的沿海港口作为研究对象。数据来源于《中国统计年鉴》《中国港口年鉴》《中国海洋统计年鉴》《中国集装箱运输年鉴》以及各省市的统计年鉴。缺失的数据采用回归替换法得到；由于超效率测算的样本数据不能为0，用0.5代替原始样本数据中的0[10]。为了保持数据的一致性，由于2006年宁波-舟山港的统计范围是原宁波港和舟山港，因此，2005年宁波-舟山港所采用的数据是原宁波港和舟山港的数据。同理，2007年烟台港的统计范围是原烟台港和龙口港，2011年厦门港统计范围是原厦门港和漳州港，也采用与宁波-舟山港相同的方法处理。主要沿海港口效率的投入产出指标的描述性统计情况见表3。

表3 测算主要沿海港口效率的投入产出指标的描述性统计情况

1.4 港口效率实证分析

运用My-DEA软件，采用超效率DEA模型对中国2005—2016年20个主要沿海港口效率进行综合测定，结果见表4。

表4 2005—2016年中国20个主要沿海港口效率值

从表4的测算结果可以看出，2005—2016年中国20个主要沿海港口效率的均值为0.886，表明中国主要沿海港口效率较高，但中国港口效率均值呈现出总体波动下降的变化趋势。2005—2008年中国主要沿海港口效率均值总体上呈现出平稳下降的趋势，其中受2008年国际金融危机的影响，2008—2011年期间呈现剧烈的波动，2010年后呈现出缓慢上升趋势，如图1所示。

图1 中国20个主要沿海港口效率值变化趋势

就各港口均值水平而言，中国20个主要沿海港口效率差异显著，20个主要沿海港口中仅有5个达到港口效率有效状态，说明中国港口还存在很大的优化升级的空间。港口效率值前5名分别为日照港、海口港、上海港、湛江港和宁波-舟山港，其中日照港效率最高，效率值为1.308。港口效率值后5位分别为福州港、厦门港、烟台港、温州港和泉州港，而最后一位的福州港效率值仅为0.465。由此可见，各主要沿海港口间效率值差异极为明显，这使得协调发展各港口之间的效率成了一项亟待解决的问题。

2 主要沿海港口效率收敛性分析

随着港口装卸技术的不断提升、管理运营模式的优化及管理经验的不断积累，港口效率值也将得到不断地提高，那么随着时间的推移，各沿海港口间的效率差距是否会逐步缩小呢？本文将使用收敛性实证检验方法进一步分析中国20个主要沿海港口效率的收敛性。

2.1 收敛性检验方法

港口效率的收敛性可分为绝对收敛、条件收敛等，其中绝对收敛包括α收敛和绝对β收敛，条件收敛即指条件β收敛。

2.1.1α收敛检验模型

α收敛指的是样本总体指标的离散程度随时间推进而减少。学术界通过采用相对平均离差、代数转换标准差和变异系数等反映离散程度的指标来进行α收敛检验[11]。本文参照杨翔等[12]的方法，选用标准差(SD)、变异系数(CV)和代数转换标准差(α)来全面分析沿海港口效率的离散程度，其计算公式为

(2)

(3)

(4)

式中：i表示港口；n为沿海港口总数；Ei表示i沿海港口效率值。若α指标数值随着时间的推移逐渐减小，则表明各沿海港口效率存在α收敛。

2.1.2β收敛检验模型

1)绝对β收敛。绝对β收敛是指各港口效率趋于相同的增长速度和稳态的水平，且低效率港口的增长速度快于高效率港口。利用面板数据对绝对β收敛进行检验，其绝对β收敛模型设定为

gi,t+1=α+βlnEi,t+ηi+μt+εi,t

(5)

式中：i表示港口；t表示年份；lnEi,t表示为i港口t年的效率值的对数形式；gi,t+1表示i沿海港口从t+1年到t年的港口效率(对数处理)的增长率，即lnEi,t+1-lnEi,t；α为截距项；β为基期效率值的回归系数；ηi、μt和εi,t分别表示反映各港口差异的个体效应、时间效应与其他干扰项。利用面板数据进行回归分析，若回归系数β显著为负值时，则说明各港口间效率存在绝对β收敛。

2)条件β收敛。条件β收敛是指因港口受自身发展条件的限制和各港口特性不同，其各港口拥有的稳态水平也不一，在长期中，使得各港口效率收敛于各自的稳态水平。港口效率值的初始状态是影响港口效率值增长率的一个因素，在绝对β收敛模型的基础上加入其他影响港口效率值的条件变量，构建条件β收敛模型为

gi,t+1=α+β1lnEi,t+β2GDPi,t+β3EXi,t+β4IMi,t+ηi+μt+εi,t

(6)

式中：GDP代表各港口所在城市的国内生产总值增长率；EX和IM分别代表各港口所在城市的货物出口总额增长率和进口总额增长率；β2、β3和β4分别表示GDP增长率、出口增长率和进口增长率等影响因素的回归系数，其余变量同绝对β收敛模型。利用i个港口t期的面板数据进行回归分析。若回归系数β显著为负值时，则说明各主要沿海港口效率存在条件β收敛。

2.2 港口效率收敛性检验

2.2.1 港口效率α收敛检验

分别采用标准差(SD)、变异系数(CV)和代数转换标准差(α)来分析各港口效率值的α收敛性，2005—2016年中国20个主要沿海港口效率的标准差、变异系数和代数转换标准差的变动情况如图2所示。

图2 中国20个主要沿海港口效率值α收敛检验结果

从图2的α收敛检验结果可以看出，3种离散程度(系数)SD、CV和α呈现出基本一致的波动趋势，均呈现“W”形的变动趋势。其中2005—2009年表现出波动下降的趋势，但受2008年国际金融危机的影响，中国各港口也受到了一定程度的冲击，2008—2009年出现断崖式下降，2010—2011年出现骤升的趋势，随后便一直缓慢下降，直至2015—2016年才表现出上升的走势。从总体上看，3种系数都表现出下降趋势，即中国主要沿海港口效率的离散程度呈现出下降的趋势，说明各沿海港口效率存在α收敛。

2.2.2 港口效率β收敛检验

根据Hausman检验结果来判断应选择固定效应模型还是随机效应模型。检验结果表明，绝对β收敛和条件β收敛均选择固定效应模型。中国主要沿海港口效率β收敛模型检验结果见表5。

从表5中的(1)列可知，lnEi,t的回归系数β值在1%的显著性水平下高度显著为负，这意味着主要沿海港口效率存在绝对β收敛，且低效率港口的增长速度大于高效率港口的增长速度。这说明中国2005—2016年20个主要沿海港口效率的差距在逐步缩小，表现出共同收敛的特征，且效率相对较低的港口表现出追赶效应。

表5 主要沿海港口效率绝对β收敛和条件β收敛检验结果

从表5中的(2)列可以看出，lnEi,t的条件收敛回归系数β值在0.01显著性水平下高度显著为负，表明中国20个主要沿海港口效率存在条件β收敛，各港口效率均收敛于自身的稳态水平。加入港口所在城市国内生产总值增长率、出口总额增长率和进口总额增长率这3个控制变量后，中国主要沿海港口效率整体上呈现出条件收敛的趋势。其中，国内生产总值增长率和出口总额增长率均表现出不显著特征，而出口总额增长率的系数在5%的显著性水平下显著为正，较高的出口总额增长率，将增加所在港口的货物出口量，有助于激励港口运用先进的装卸技术、先进和管理经验和改善港口运作管理模式，从而促进港口效率条件收敛于自身稳态水平。

3 结论与启示

运用2005—2016年中国20个主要沿海港口的面板数据，研究中国主要沿海港口效率及其收敛性。结果发现：沿海港口效率总体水平较高，但港口间的效率差异显著；沿海港口总体的效率存在α收敛、β收敛，在整体上港口效率差异呈显著缩小趋势，且效率相对较低的港口表现出追赶效应。

基于以上研究结论，提出如下政策建议：

1)缩小沿海港口效率差距以促进港口间协调发展。首先，福州港、厦门港和烟台港等中低效率港口要以缩小港口差异为目标，以长远眼光优化港口发展规模，追求规模效益最大化。其次，要通过日照港、海口港和上海港等高效率港口发展的领先优势推动福州港、厦门港和烟台港等中低效率港口的发展，鼓励中低效率港口借鉴学习高效率港口先进的管理经验、港口装卸技术和运作管理模式，推动其港口效率向中高效率港口平均水平靠拢。最后，中低效率港口要充分发挥自身港口所具有的优势，利用其优势来弥补港口效率低的不足，如厦门港应充分利用天然深水、自然条件优越和经济腹地等优势，以缩小与高效率港口的发展差距，从而努力促进其效率与高效率港口协调发展。

2)扩大沿海港口出口贸易额以推动港口效率增长。出口总额增长率是促进港口效率增长的主要因素，因此主要沿海港口所在城市要以扩大沿海港口出口贸易额为核心任务，来提高港口效率。为此，沿海港口所在城市政府应加大对出口企业的扶持力度，鼓励企业扩大外贸出口规模。