一种基于模型预处理的SCUC快速求解方法

段睿钦，蒋 燕，李秀峰，高道春，吴 洋，赵珍玉，苏向阳

(1.云南省电力调度控制中心，昆明 650011；2.北京清能互联科技有限公司，北京 100080)

近年来由于电力市场的快速发展，计及安全约束的机组组合 (SCUC) 问题受到了越来越多的关注，而日益复杂的电网模型给SCUC问题带来了一系列新的挑战。SCUC是在满足电网潮流、线路传输容量等一系列约束前提下以最小化运行成本为目标的优化求解问题。SCUC可以被抽象为一个混合整数线性规划(MILP)的数学问题，但MILP问题已经被证实为NP-hard问题，难以快速求解[1]。对于这类问题最常见的手段是采用商业求解器进行求解，其主要手段是基于预处理和启发式等方法对模型进行缩减，使用分枝割平面法加速求解[2]。但求解器的预处理存在了诸多限制，如何建立高质量的MILP模型一直是研究热点[3-5]。

文献[6-7]通过引入新的0～1变量来添加更多的切割约束，使得模型可行域更小，但是没有考虑多时段。文献[8]在文献[6-7]的基础上进行了改进，虽然计及多时段且模型更加紧凑，但模型的规模变得更加庞大。文献[9]对机组参数进行假设，提出了短期多时段约束的改进模型，但是没有模型来源没有给出具体推导。文献[10]在文献[9]公式的基础上进行了推导，但没有给出数值结果。文献[11]对上述内容进行了总结改进，但是对于单机相关约束仍存在改进空间[12]。

现基于以上研究现状，从SCUC模型的物理意义出发，分析改进后约束对SCUC模型求解速率的影响，对模型中爬坡约束及网络约束分别做了紧缩处理，使得模型更加紧凑。最终通过IEEE39节点和IEEE118节点多场景算例对模型的正确性和可行性进行了验证。

1 原始SCUC模型

SCUC模型主要包含以购电成本最小的目标函数，以及系统约束、机组相关约束、网络约束。传统的SCUC模型[13]为

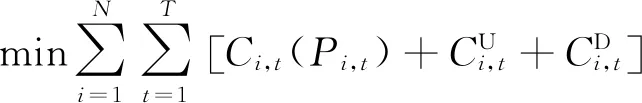
(1)

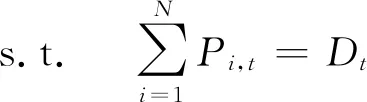
(2)

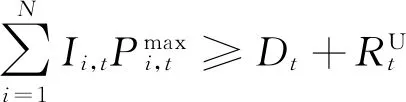
(3)

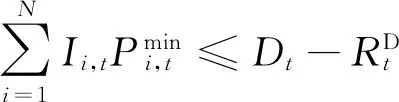
(4)

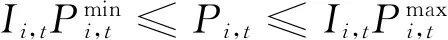
(5)

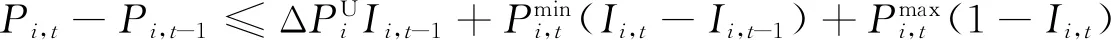
(6)

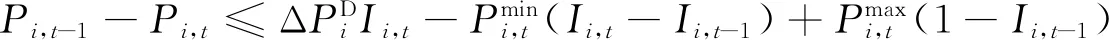
(7)

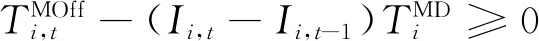
(8)

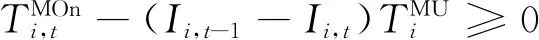
(9)

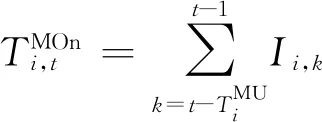
(10)

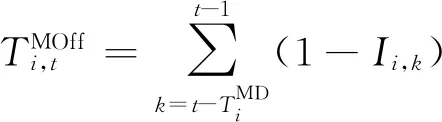
(11)

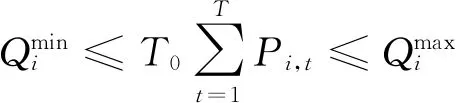
(12)

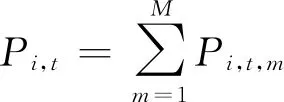
(13)

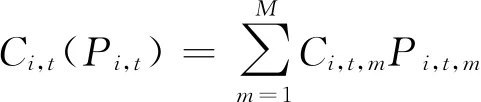
(14)

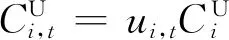
(15)

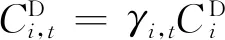
(16)

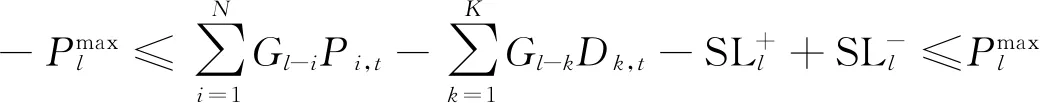
(17)

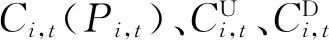
2 爬坡约束预处理

多时段的SCUC问题中，一些机组在特定时段由于电网传输特性限制不会达到爬坡上下限，因此对应的爬坡约束存在紧缩的可能。对于单机全时段SCUC的建模，输入数据机组上下限、爬坡速率等采用质数或相互间没有公约数的特征整数值，可以通过PORTA[11]算法生成单机全时段SCUC模型所有约束构成的多边形顶点，根据整数解顶点反推出紧缩的SCUC约束，基于单机推导出的紧缩约束也适用于所有机组。因此，根据机组爬坡速率的不同，可以添加如下约束空间[11]：

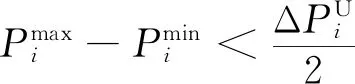
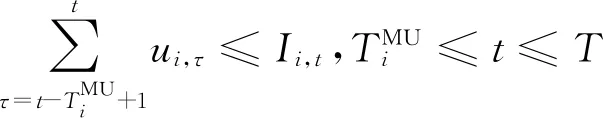
(18)

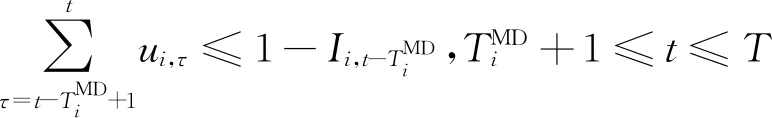
(19)

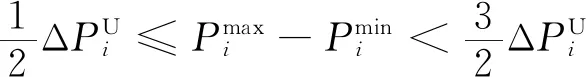
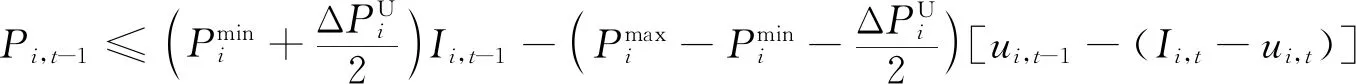
(20)

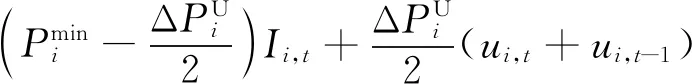
(21)

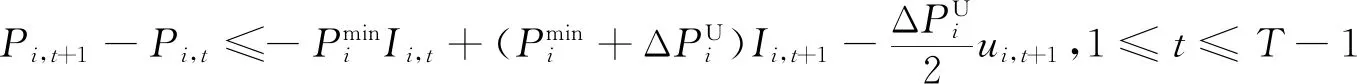
(22)

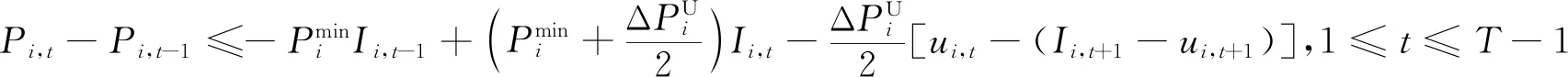
(23)

(24)

(25)

(26)

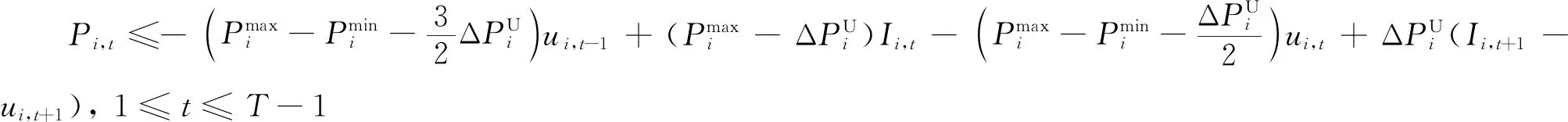
(27)

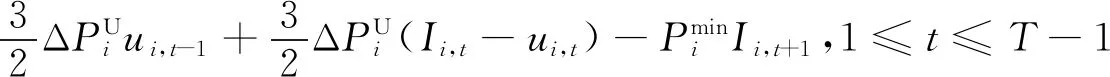
(28)

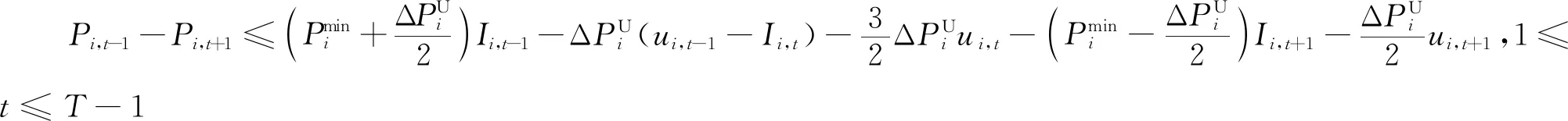
(29)

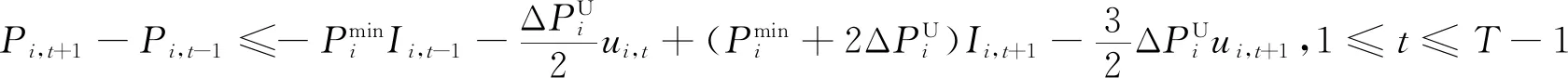
(30)

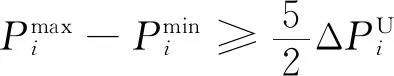
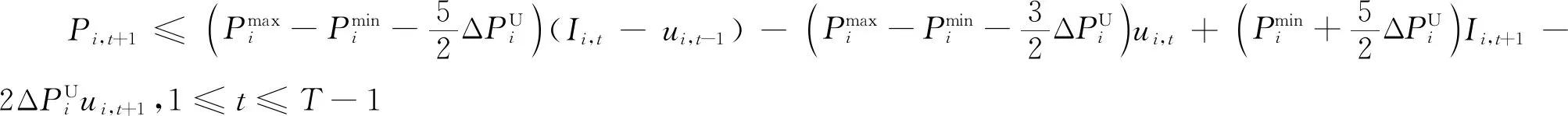
(31)

3 网络约束预处理

爬坡约束属于单机约束，机组间的爬坡约束没有影响，单机推导出的紧缩约束也适用于所有机组。不同于单机约束，潮流上下限约束属于系统约束，反映了机组之间的关系，不能通过第2章的方法处理。

实际上在求解SCUC问题时，很多线路潮流上下限约束自始至终也没有生效，单纯依赖商业求解器的预处理难以有效剔除这些约束，导致模型求解速度降低[12]。

由于电网规划与城市发展原因，一部分线路可能永远不会出现传输阻塞的情况。另外存在一部分线路，当该线路阻塞时，一定存在一条或多条线路出现阻塞的情况。对于这两种线路，均可以通过预处理的方式来削减模型约束的规模。

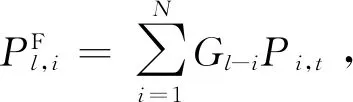
1)找到线路l所有节点的转移分布因子Gl-1，2,3，…将这些转移分布因子按次序从大到小排列。

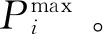
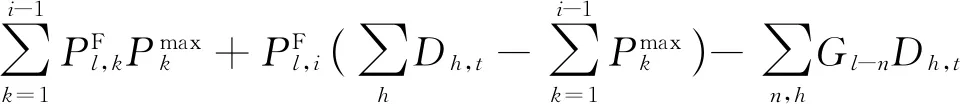
(32)

4 仿真分析

为验证预处理方法的有效性，在GAMS[14]平台上搭建了数学模型，调用CPLEX12.6[15]求解器进行求解。分别对IEEE39节点和IEEE118节点进行了测试，测试模型为原始SCUC模型(OM)，预处理爬坡约束的SCUC模型(PRM)，预处理爬坡和网络约束的SCUC模型(PRFM)，所有算例测试基于24 h 96时段，每个时段15 min。对IEEE39节点系统进行测试时，设置如下不同场景进行验证预处理的有效性。

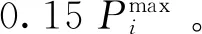
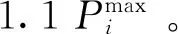
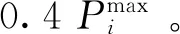
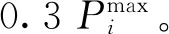
表1给出了不同场景下不同模型的优化对比，主要包括了计算效率的对比、模型约束数量的对比、求解器的最终优化跟节点数目对比以及目标函数值的对比。从表1可以看出，PRM相较于PFM可以大幅度缩减优化求解器的搜索根节点的数目，意味着PRM应该有更高的效率。从表1计算效率的对比结果来看，虽然不同场景下PRFM的求解速度上都快于OM求解速度，但PRM和PFM的求解速度也基本上快于OM的求解速度，但存在个别场景，PRM和PFM的求解速度稍慢一些。这是由于系统规模在模型预处理之后，可行域被割裂成更多的子集，导致在小规模系统时会出现更多次的搜索，降低了求解速度。

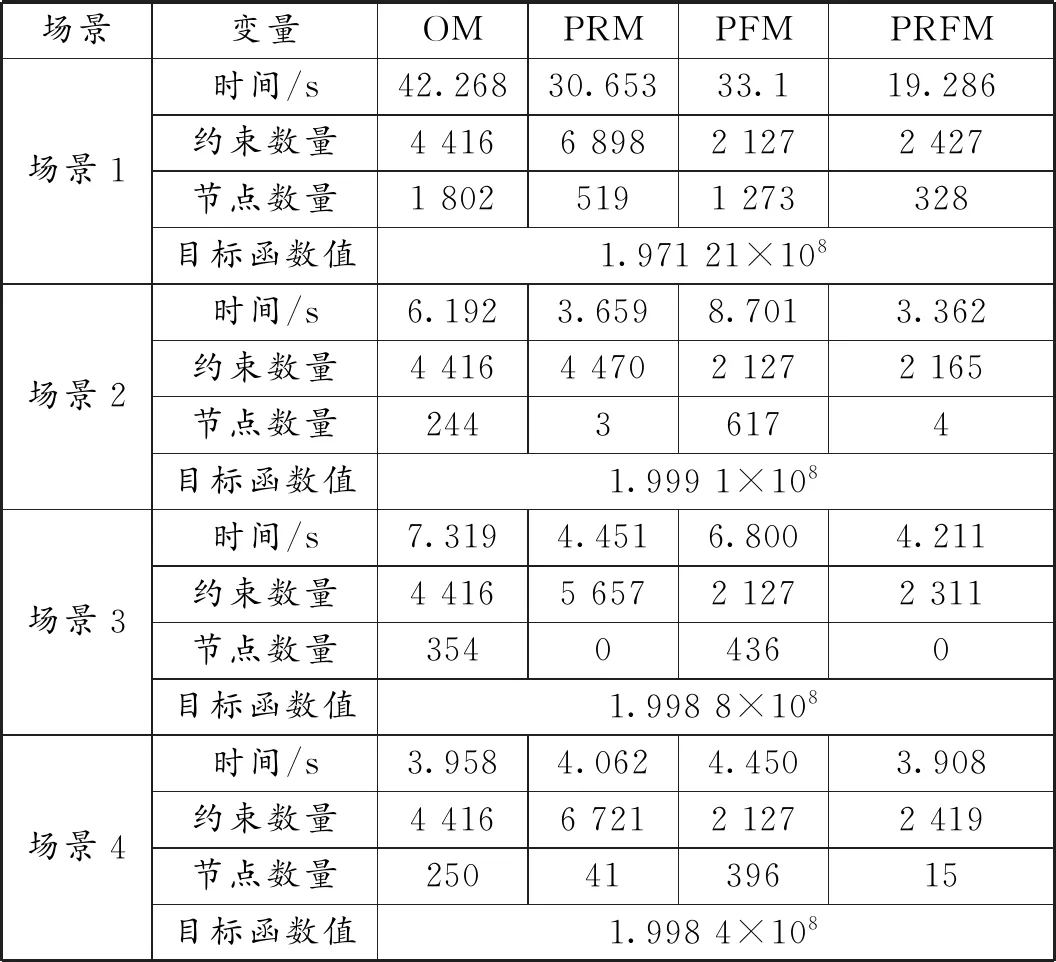
表1 IEEE39节点中不同场景下不同模型的结果对比

为验证所提模型的正确性及可行域切割导致速度变慢的问题，对IEEE118节点系统进行测试，设置如下不同场景进行验证预处理的有效性。

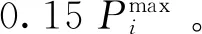
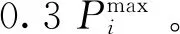
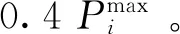
由于IEEE118系统节点较多，如果绝对gap值取0，存在阻塞的情况下求解时间可能陡然增加到几十小时，因此设置相对gap值为0.1%。在保证最优解相当的情况下比较不同场景下的模型，见表2。从表2中可以看出，3个场景下，PRFM相对于OM的计算效率都有明显提升。无论是PRM还是PFM的求解速率均要快于OM。但在场景2中，OM与PRM的计算效率相差微小。虽然在优化节点数上PRM有了近一半的缩减，但是整体求解效率并没有得到明显改善。这是由于大规模系统中也会出现无效搜索或者是零碎的细化搜索，虽然整体模型削减后计算效率的提升可以在一定程度上弥补这些无效搜索消耗的时间，但并没有明显的效率提升。在求解结果方面，3种场景下不同模型的gap值设置均小于0.1%，模型之间的结果差异在0.02%以内，差异在可接受区间内。

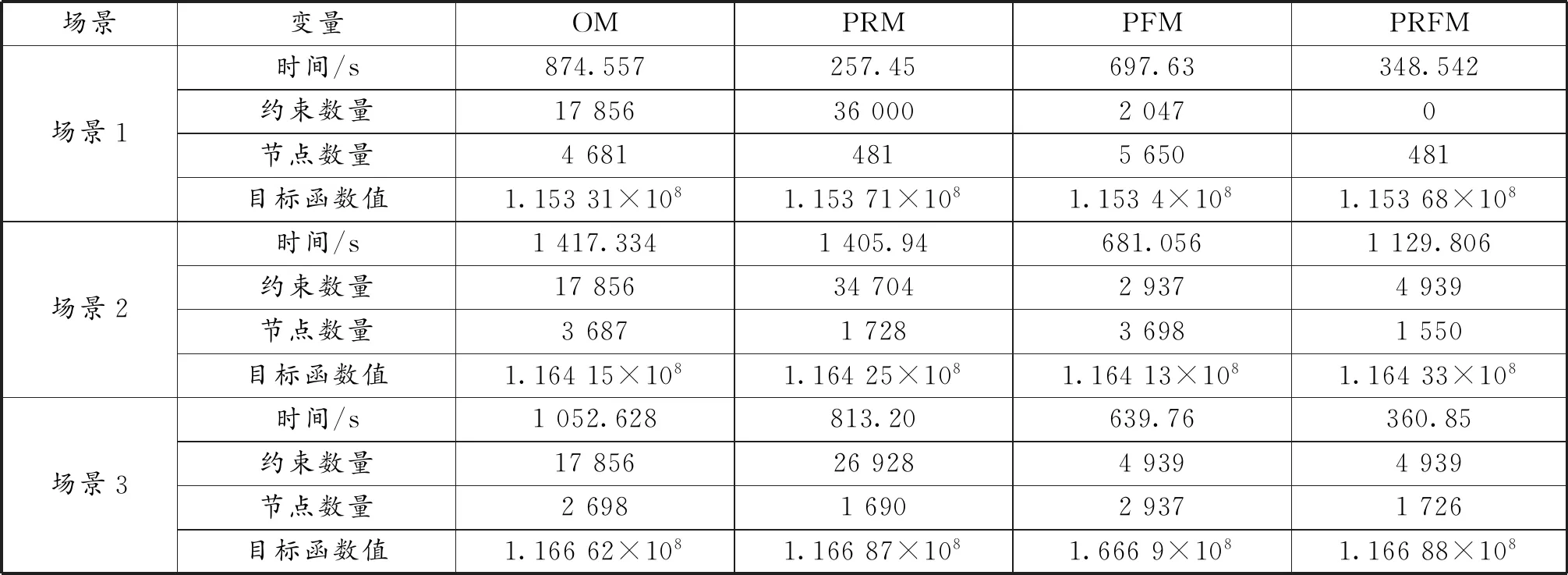
表2 IEEE118节点中不同场景下不同模型的结果对比

不同模型的预处理时间如图1所示。从图1中可以看出，PRM预处理时间最快，在5 s左右，PFM和PRFM的预处理时间都在300 s左右。预处理时间与整体求解时间相比，预处理时间波动性小，时间量级可以接受，因此模型预处理的理论可行性较强。如果采用预处理的方法处理轻量级的模型，可以选择PRFM，在求解时间上具有稳定且较好的改进效果。在预处理较大规模的系统时，如果预留预处理的时间较小，建议采用PRM；如果原模型阻塞严重，建议采用PFM；如果阻塞较轻，可以采用PRFM。

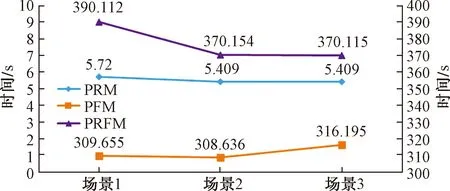
图1 不同模型预处理时间对比结果

5 结论

SCUC的快速求解一直是电力市场的重要环节之一，为了能加速模型的求解效率，从预处理的角度对现有的SCUC模型进行改进。针对电网的物理特性，分别从机组之间相互独立，提出机组爬坡约束的预处理。从线路潮流可能永远无法达界的角度提出了对网络约束的预处理方式。在仿真分析部分，在IEEE39节点和IEEE118节点依据不同场景分别对PRM、PFM、PRFM的求解效率和解的质量做了对比分析，验证了所提模型的正确性和可行性。并给出了不同模型的应用场景。