基于滚动灰度模型的小样本数据预测北京第三产业增加值

杨 洋，张玉浩，刘 礼

(1.国家电网有限公司 华东分部后勤管理中心，上海 200120；2.重庆大学 大数据学院，重庆 401331)

准确把握未来的经济趋势对制定有效的政策和计划至关重要。第三产业不仅是产业结构的重要组成部分，而且与人民的生活质量和收入息息相关。第三产业的概念是根据产业结构和社会经济发展提出的[1]。大约在1979年，中国政府开始关注第三产业，但实际上到1985年才开始关注它，随后制定了第三产业分类标准，并于2003年重新分类。其相应的统计数据库已建立并可以在线使用。随着中国经济从高速增长阶段转变为高质量发展阶段，第三产业在国内生产总值中的比重不断提高，因此受到了中国政府的重视。但是，作为发展中国家，第三产业的发展仍然远远落后于发达国家。例如，在美国和日本，第三产业份额和劳动力份额的增加值分别达到GDP的70%～80%和60%～70%，而中国为42%和16%[2]。中国正在按照霍夫曼定律和佩蒂·克拉克定律、Leontief的投入产出分析、Rostow的成长阶段理论、Kuznets[2-5]、Chenery标准[6]和“飞鹅”理论[7]所揭示和证明的产业结构发展与演变的规律进行工业化。因此，第三产业的发展对中国的整个经济发展具有重要意义，甚至影响到世界经济。

1 第三产业现状及政策制定

1.1 中国第三产业现状

国家统计局记录了1978—2019年中国第三产业增加值的增长情况，其中包括运输、仓储和邮政、批发和零售业、酒店和餐饮服务等传统产业，以及新兴行业，如金融中介、房地产和其他服务。传统服务业的比例正在下降，而新兴产业已成为提升第三产业增加值的主要动力。

1.2 北京第三产业现状

北京的第三产业在过去几年中发展迅速。在将近32年的时间里，北京的第三产业一直领先于其他地区，年平均增长率为第三产业的21%。在过去的10年中，北京的第三产业在GDP中所占的份额在中国所有发达城市中排名第一。到2019年，这一比例达到了87.8%，遥遥领先于其他两个发达地区，即上海(72.7%)和广东(55.5%)。

北京第三产业增加值中传统的运输、仓储和邮政以及批发零售贸易和酒店餐饮服务的份额从1978年的27.15%和32.12%逐渐下降到2019年的2.9%和1.5%。相反，新兴产业的份额，即金融中介、房地产和其他服务分别从1978年的7.41%、3.3%和30.2%增至2019年的18.5%、7.4%和45%。可以看出，新兴产业的发展最快。近年来，北京第三产业的发展不稳定，尤其是在2007年全球金融危机爆发以及2020年世界疫情后，第三产业从2019年到2020年(前三季度)同比只增加了0.1%。

1.3 政策制定

在中国经济增长放缓背景下，必须做出一些政策变化，并推进结构性改革。可以根据上述有关第三产业的历史数据中发现的规律来调整政策。例如，尽管可再生能源增长迅速，但仅占第三产业的一小部分(约10%)，对第三产业影响不大。金融中介的增长显著低于批发零售的增长，但所占比例相对较大(18.5%)。这些结果表明，金融业在北京第三产业中的贡献超过可再生能源，因此建议优化金融业的发展结构。另外，增长的波动性给政策制定带来了困难。成功的政策应该捕捉到这种波动，并使用预测结果前瞻性地审视未来的发展，以便在下一个短期经济时期做出正确的评估。在对现有样本数据建模时，波动部分将影响对未来短期经济数据的预测。因此，预测模型应消除此类波动，以提高预测精度。

本文重点关注第三产业中的数据建模和预测问题。此外，本文应用的预测方法还可以用于其他经济领域，其数据序列与第三产业中的数据序列相似，即样本数量少且序列不规则。

2 经济预测相关模型

根据时间序列理论，数据的顺序似乎是高度非线性、不规则和不稳定的，但是呈趋势性上升。此外，第三产业年度或季度报告相应的数据序列通常很短。另一方面，政策制定不仅需要单个数据点的预测，还需要第三产业趋势的估计。因此，很难准确地预测中国第三产业的发展。提出一个有效的预测模型来处理混沌数据成为预测的关键。

2.1 预测模型的分类与优缺点

经济预测领域的预测模型可以分为3类：因果模型、学习模型和时间序列模型。

因果模型(如多元线性回归分析和计量经济模型)通过历史观察进行建模，并使用实时观察进行推理，假定因变量和自变量之间的历史关系在将来仍然有效，包括多元线性回归分析和计量经济学模型，假设自变量可以解释因变量的变化。其局限性是实时观测(自变量)的不可用性和不可靠性。

时间序列模型假设历史会重演，其预测是指根据从过去和当前数据点获得的信息对系统的未来值进行预测的过程。用于时间序列预测的两种主要技术是基于统计和基于人工智能(软计算)的方法。随着机器学习技术的成熟，诸如深度神经网络(DNN)和支持向量机(SVM)的学习模型也被用于经济预测。广泛使用的软计算方法包括神经网络[8]、支持向量机(SVM)[9]、模糊系统、线性回归、卡尔曼滤波[10]、隐马尔可夫模型(HMM)。所有这些方法都用于更新模型参数。近年来，提出了几种混合模型[11-12]，以提高预测精度。不幸的是，这些软计算方法需要大量的训练数据和相对较长的训练时间才能实现稳健的泛化[13]。对于经济预测而言，由于在经济时间序列上具有高度非线性、不规则和非平稳的特性，因此既无法通过常规的线性统计方法，也无法通过人工神经网络来构建模型[14]。

相反，时间序列统计模型假设历史经常重演，仅需要特定观测的历史数据。因此，时间序列统计模型已广泛应用于预测。灰度预测模型是基于灰度理论建立的时间序列统计模型，用于处理不确定和粗糙数据集。灰度理论可以处理不完整、不足和离散的数据，对有噪声数据和丢失数据情况下更适用。灰度模型已经证明了预测不规则和非线性经济时间序列数据的有效性。研究显示[15]，在处理短期预测时，其性能优于其他预测方法。对于长期的预测，灰度模型需要改进。将残差修正和残差神经网络估计相结合的方法[16]可以提高原始灰度模型的准确性。然而，这种方法需要很长的训练时间。

2.2 滚动灰度预测模型在其他领域的应用

滚动机制是提高灰度系统模型性能和处理噪声数据的最有效方法之一。Tang等[17]使用滚动机制来提高灰度模型用于教育支出的预测准确性。Zhao等[18]提出了一种具有微分进化算法的滚动机制来预测中国农村家庭的人均年纯收入，并得出结论，该机制优于其他传统的灰度预测模型。许多研究者[10-12]通过优化各种模型参数来改进滚动灰度模型，例如煤炭产量预测和半导体行业产量预测。

3 滚动灰度预测模型

本文应用滚动预测模型(RGM)预测北京第三产业增加值，通过实现数据预处理阶段的指数性预处理能力，提高预测的准确性。

3.1 模型描述

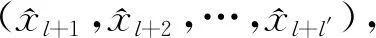
对于每个预测周期t，首先通过迭代算法找到最佳值。在此迭代中，样本数据被分为两个部分，即训练数据序列[x1(t),x2(t),…,xq(t)]以及验证数据序列[xq+1(t),xq+2(t),…,xq+d(t)]，其中q是用于构建RGM模型的样本数据量，而d为需要预测的数据量，并通过以下适应度函数验证模型：

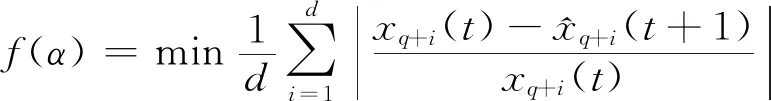
(1)

注意q+d=l。本文中，利用粒子群迭代算法优化参数α，即在适应度函数中具有最小值f(α)将被选作当前预测期内RGM模型的最终参数。

然后，RGM使用一系列长度为l的样本数据来预测长度为n的未来数据序列，从而建立具有最佳参数α的RGM模型。重复此过程，直到可以预测所有将来的l′个数据。

3.2 应用示例

使用2000—2015年的第三产业样本数据来预测2016—2020年的下一个5年数据。在这种情况下，l=16，l′=3。令n=3，q=11，d=5。

在第一个预测迭代周期，将样本数据序列分为两部分以调整参数α，即训练数据序列[x2000(0),x2001(0),…,x2010(0)]和验证数据序列[x2011(0),x2012(0),…,x2015(0)]。对于每个候选参数α，使用带有该参数的RGM模型构建模型，以预测2016—2020年的数据，即

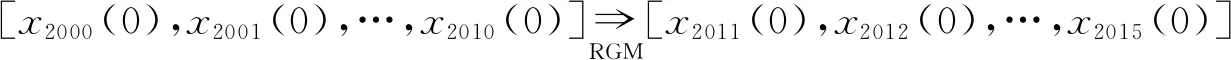
(2)

通过适应度函数估算当前参数α，即

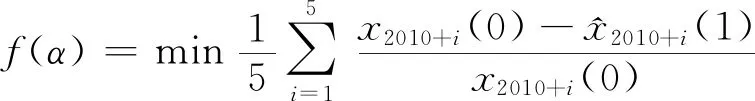
(3)

在此迭代中,具有最小适应度值的f(α)作为最佳参数，用α(1)表示。然后建立具有此参数的RGM模型，以预测2016—2018年的数据，即

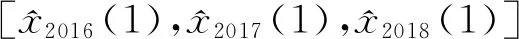
(4)

在第2个预测迭代周期，由RGM模型估算出最佳参数α(2)，即

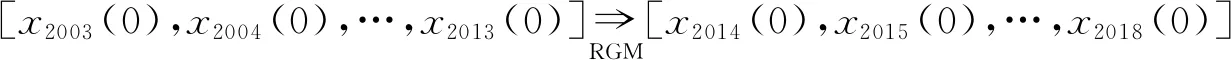
(5)

和适应函数

(6)

最后，通过RGM模型预测2019—2021年的数据，即

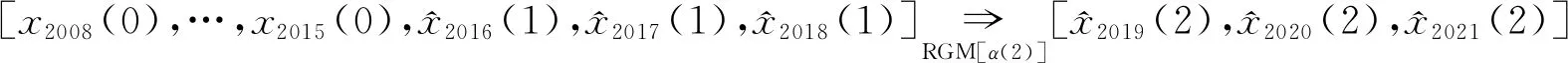
(7)

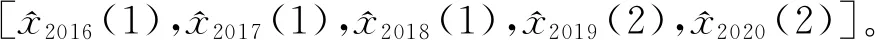
4 预测

4.1 数据集

采用1996—2019年北京第三产业数据集，来自中国国家统计局公开数据。该数据集划分为6个子行业，即运输、仓储和邮政、批发零售及酒店餐饮、金融中介、房地产和其他服务。由于这些行业在1996年之前增长相对缓慢，故在本次预测中，仅考虑1996年之后的数据。

4.2 评价标准

使用平均绝对百分比误差(MAPE)进行预测模型评估，其为公认的预测准确性的度量标准。MAPE的定义如下，其相应标准在表1中列出。

表1 MAPE评价标准

(8)

4.3 预测结果

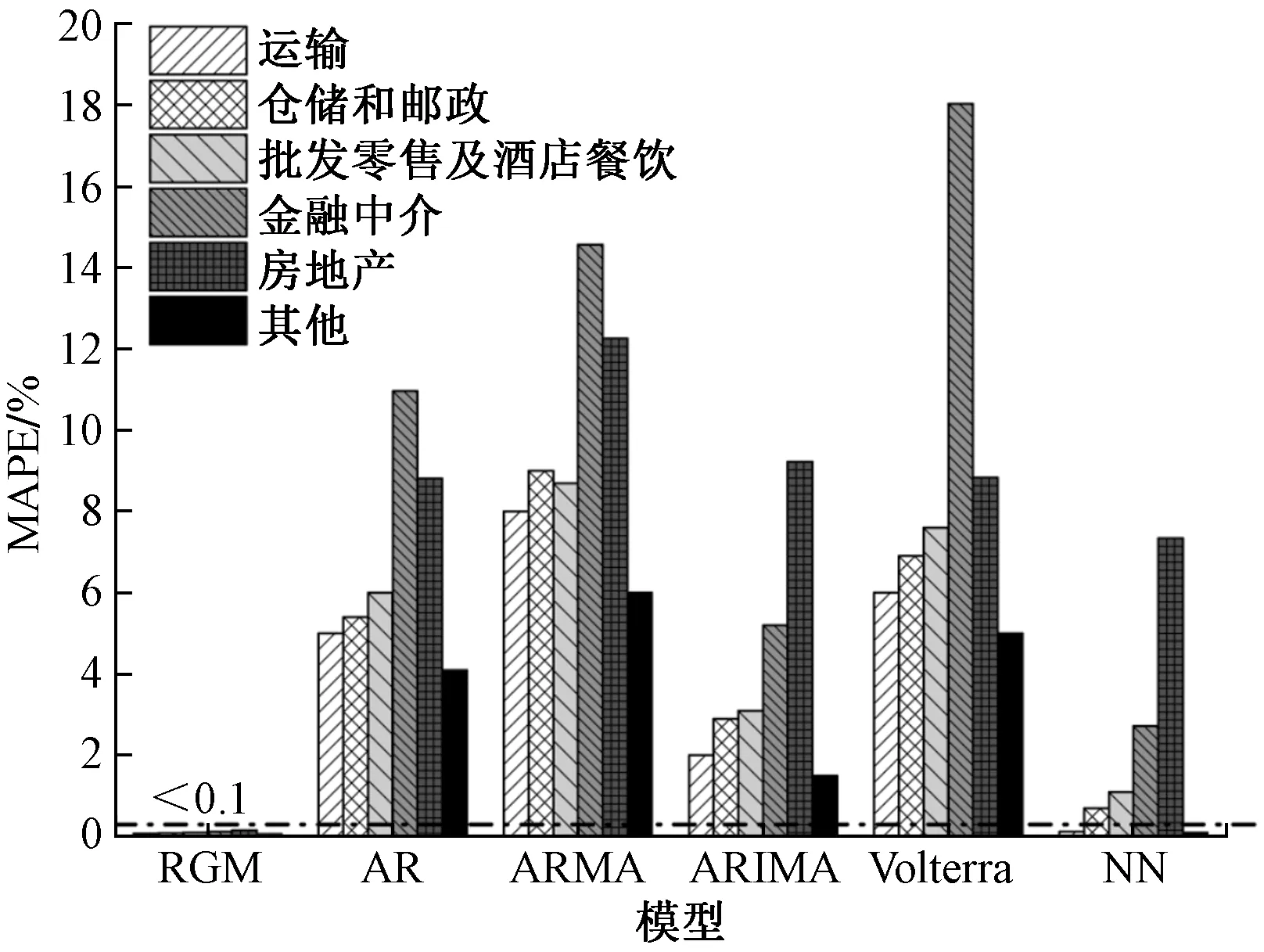
图1 RGM与其他模型在MAPE预测评估中的比较结果

将RGM与自回归模型(AR)、自回归滑动平均模型(ARMA)、差分整合移动平均自回归模型(ARIMA)、Volterra模型以及神经网络(NN)5个著名的经济预测模型进行比较。图2显示了这6个模型在MAPE上的比较结果。很明显，RGM在所有6个子行业预测上都优于其他模型。在所有子行业数据预测中，RGM的MAPE均小于0.1%。总体而言，ARIMA和NN在评估指标上也获得了可接受的结果，而其他模型的MAPE也都在20%以下。

5 结论

本文专注于预测北京第三产业增加值，以帮助决策者制定有效的政策和计划。提出了一种滚动灰度模型预测经济时序数据，该模型不仅可以准确地预测单个数据点，而且还可以在短期且波动的样本数据训练序列下准确地预测趋势。这对于合理地预测非线性、不规则和非平稳序列是可行的。在北京第三产业的6个子行业上对RGM模型与其他5个竞争模型进行了评估和比较，发现大多数模型都在长期趋势中波动上升，预测结果也表明RGM通常胜过其他模型。此外，预测北京的第三产业在未来5年内的增长率将下降到一定程度。建议政策制定者可以调整当前的经济政策。在未来研究中，将使用更多的数据集来进一步探索可能影响预测模型性能的经济因素。