一种用于机场场面监视的高精度位置解算方法
王 力,于 雷
(中国民航大学a.职业技术学院;b.电子信息与自动化学院,天津 300300)
多点定位系统[1]作为民航五大监视技术[2]之一得到了中国民用航空局(简称民航局)的大力推广。多点定位系统采用时间差定位技术,通过测定监视点发射信号到各基站的时间差来确定监视点位置,达到对监视点的实时高精度可靠监视。这种监视方法依赖于信号到达基站时间差的准确测量及可靠的位置解算算法。在民航机场场面监视应用[3-5]中,能够实时精确地解算监视点位置是研究的重点课题之一。
多点定位方法现有的解算算法包含解析法和智能优化算法。在解析法中:Chan 算法[6]具有计算量较小、不需要迭代运算等优点,但在非视距环境下定位精度存在不足;Friedlander 算法、球面相交算法、球面插值算法都没有考虑变量之间的相关性,很难实现最优估计[7];Taylor 级数展开法[8-9]则需要借助一个与实际较为接近的初始位置值进行迭代运算,才能在短时间内解算,得到精确目标位置,在初始位置值选取不好的情况下,易导致算法不收敛。Chan 算法、Taylor 级数展开法是解析算法中定位性能最好的两种算法。
除了传统的解析算法之外,很多智能优化算法也被应用到多点定位解算中。2007年,粒子群优化(PSO,particle swarm optimization)算法首次被Lui 等[10]用于解决多点定位位置解算问题,可在不设定位置初始值的情况下进行位置寻优,但传统粒子群算法易陷入局部最优。Rosic′等[11]将改进遗传算法(IGA,improved genetic algorithm)应用于到达时间差(TDOA,time difference of arrival)的定位解算。通过对实际问题进行数学建模,建立相应的适应度函数,利用适应度值来择优选取更加靠近监视点的位置。该过程省略了传统解析算法中复杂的计算过程,不用求矩阵的逆运算,但算法后期普遍存在收敛速度过慢、易陷入局部最优等问题。
针对上述问题,提出一种自适应弹射粒子群算法与Taylor 级数展开法的联合算法(简称联合算法)。该算法首先对多点定位系统进行数学建模,利用监视点的最大似然估计函数建立粒子群算法的适应度函数。针对粒子群算法易陷入局部最优的问题,将小生境技术[12]引入标准粒子群算法中,对小生境中的粒子进行弹射,保证种群的多样性,同时改进惯性权重的赋值方式,采用自适应赋值策略。自适应小生境弹射粒子群算法搜索的定位结果作为Taylor 级数展开法的初始参考点,再通过Taylor 级数迭代,实现对繁杂机场场面监视点的精确定位。
1 多点定位数学模型
三维空间中存在N个不同位置的接收站,第i个接收站的位置为si=(xi,yi,zi),其中i=1,2,…,N,监视点位置为u=(x,y,z),监视点位置u到接收站位置si的距离为ri=‖u-si‖2。不失一般性,选取s1作为主接收站,位置为s1=(x1,y1,z1),其余为辅接收站。在信号视距传播情况下,根据TDOA 定位原理可得
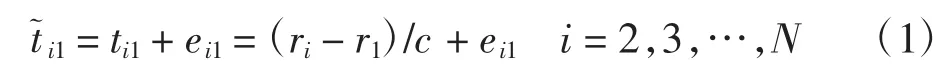
式(1)两端同乘信号传播速度c,可将TDOA 方程转化为对应的距离差(RDOA,range difference of arrival)定位方程,即
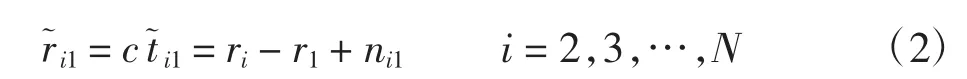
式中ni1=cei1为相应的RDOA 测量误差。
令ri1=ri-r1,则式(2)可表示为

令r=h(u),则有,根据最大似然估计准则[13],对u的最佳估计为使观测样本的似然函数取得最大值的估计,即

对目标定位问题而言,u的最大似然估计是在获得观测的条件下,在区域Du内找到最可能的u的位置。
若假定测量噪声为零均值的高斯噪声,则式(4)可表示为
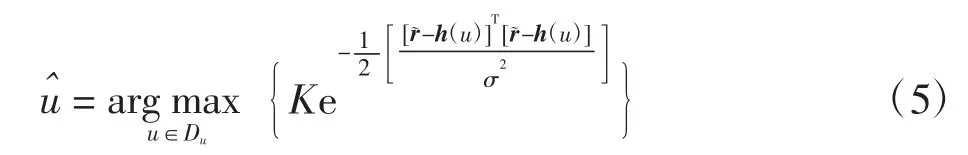
式中K为常数系数。式(5)可进一步简化等价为
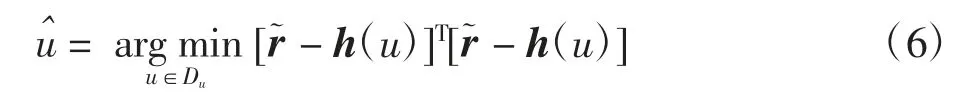
根据建立的多点定位系统数学模型及最大似然估计准则,可得到关于监视点u的估计函数,如式(5)所示,可进一步等价为式(6)。这是关于监视点位置u的非线性函数,运用传统的解析法很难求解该非线性二次方程,计算量较大。
2 改进的自适应弹射粒子群算法
2.1 粒子群算法
一群随机初始化后的粒子组成种群,利用系统中个体间的协作和竞争,实现粒子与粒子之间及粒子自身的逐步迭代寻优搜索。
实现这种算法通常需设置一个搜索空间,种群规模为M,维数为d,xi=(xi1,xi2,…,xid)表示第i个粒子的位置,vi=(vi1,vi2,…,vid)表示第i个粒子的速度,i=1,2,…,M。传统粒子群算法第i个粒子速度和位置的更新迭代公式如下

式中:pi=(pi1,pi2,…,pid)表示当前粒子i自身的最优位置;pg=(pg1,pg2,…,pgd)表示当前所有粒子的最优位置;c1、c2表示学习因子,用以调整粒子自身经验与社会(群体)经验的权重,常取c1=c2=2;r1、r2为[0,1]区间内的随机数,起到使粒子以等概率的加速度飞向个体最优位置及粒子全局最优位置的作用;ω 为惯性权重;k为迭代次数。
2.2 自适应惯性权重的改进
粒子群算法中,惯性权重ω 的选取直接影响粒子的搜索能力,进而影响算法性能,因此可通过ω 来控制粒子的全局搜索与局部搜索能力。目前,大多数算法均是采用ω 递减策略来动态调整权值,但这种递减法会使算法在性能上存在不足:①在粒子迭代寻优的初期,已有粒子处于最优值附近,但由于ω 过大导致粒子局部搜索能力不足,致使粒子不能在最优解周围细致寻优;②当进行到算法迭代的末期,此时ω 较小,粒子只能在当前位置的小范围内进行搜索,致使粒子没有足够大的速度突破局部最优的限制,以至于陷入局部最优。针对以上不足,引入种群平均适应度,通过比较当代粒子的适应度值与平均适应度值的大小来动态调整惯性权重,即
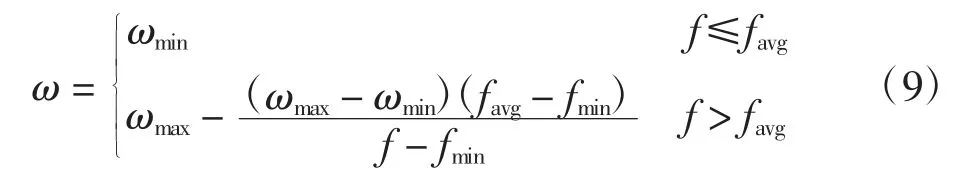
式中:ωmax、ωmin分别为最大惯性因子和最小惯性因子;f为粒子当前的适应度值;favg、fmin分别为当前所有粒子的平均适应度值和最小适应度值。
2.3 小生境弹射策略
传统粒子群算法中,全体粒子始终向个体最优粒子和全局最优粒子方向移动,使得后期粒子集中在小范围内,导致粒子全局搜索能力下降,粒子群算法陷入局部最优区域或停滞。针对该问题,在粒子群算法内嵌入小生境弹射机制,即
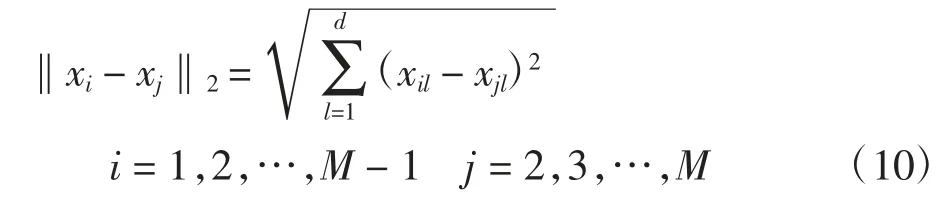
当‖xi-xj‖2小于小生境半径L时,比较个体xi、xj的适应度值。在最小化问题中,粒子适应度值越小,则表示当前位置越优,则对适应度值较大的粒子进行弹射,即

式中:a为[-1,1]之间的随机数;v 为弹射速度常量;nij为xi、xj适应度值较大者的粒子序号。通过上述操作对适应度大的粒子进行弹射,使粒子飞出小生境半径区域。
3 Taylor 级数展开法
Taylor 级数展开法[14]是一种迭代性的求解算法,在每次迭代之后将计算所得的定位误差赋给下一次迭代的位置,达到改变位置的目的,依次迭代最终逼近目标位置,算法具体求解过程如下。
先设定一个监视点的初始位置p0=(x0,y0,z0)及迭代条件(门限值ε),将

在p0处进行Taylor 展开
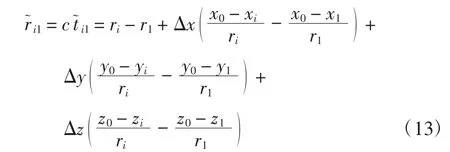

其最小二乘解为

将得到的位置估计误差δ 引入到下一次迭代中,来改变下一次迭代的监视点位置的初始值,即

重复以上迭代过程直到满足门限要求
4 联合算法流程
多点定位位置解算算法中,传统解析法Taylor 级数展开法的迭代值受初始位置选取的影响,初始位置选取不好可能会使算法不收敛或迭代次数增加。传统的粒子群算法应用于多峰值非线性情况时,在寻优过程中易出现早熟、陷入局部最优等问题。为了克服上述问题,通过自适应惯性权重和小生境弹射策略操作对传统粒子群算法进行改进,再与Taylor 级数展开法进行联合运算,具体求解步骤如下。
步骤1根据式(6)可确立适应度函数为
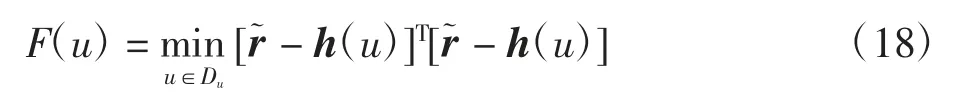
步骤2对粒子群算法各参数进行初始化,并确定Taylor 级数展开法位置门限值ε。
步骤3依据式(7)、式(8)更新每个粒子的速度和位置,更新粒子个体和全局最优位置。
步骤4依据式(18)计算每个粒子适应度值,并按照适应度从小到大的顺序对粒子进行排序,得到最小适应度值fmin,并计算出平均适应度值favg,依据式(9)计算惯性权重ω。
步骤5判断是否已达到最大迭代次数。如果已达到,则输出适应度值最小的粒子位置作为Taylor 级数展开法的初始参考点并开始Taylor 迭代;如果未达到最大迭代次数,则执行步骤6。
步骤6依据式(10)计算任意两粒子的距离并判断是否小于小生境半径L。如果小于小生境半径则依据式(11)和式(12)对适应度值较大的粒子进行弹射,然后执行步骤4;如果大于小生境半径,则执行步骤3。
联合算法流程图如图1所示。
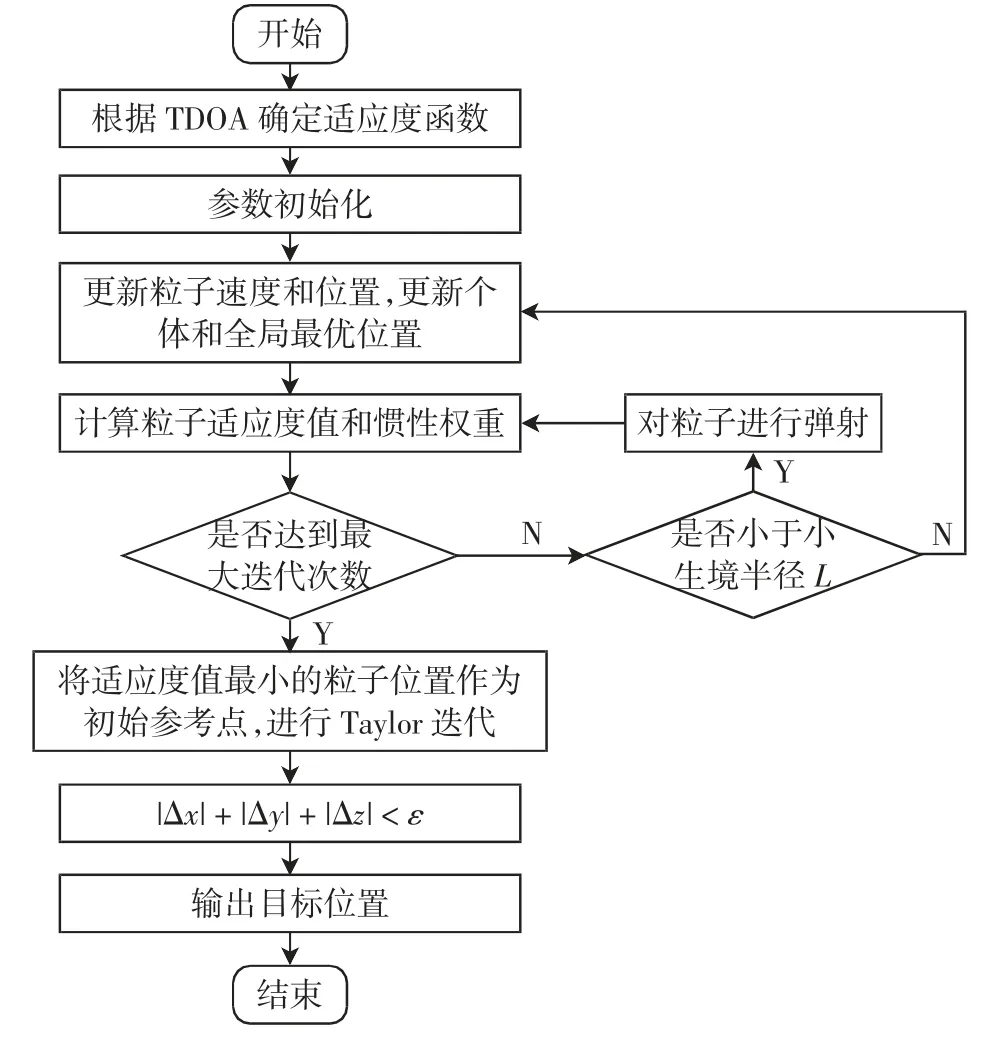
图1 联合算法流程图Fig.1 Flowchart of joint algorithm
5 仿真分析
TDOA 定位本质是通过测量监视点到基站(接收站)的距离差而实现位置解算,在机场场面多点定位系统中,监测点可以是静止的飞机也可以是运动的小车,因此,仿真分析以平面上的移动目标定位为基础,采用正方形布站方式,横纵区间均为[-1 000,1 000]。各基站坐标分别为BS1(800,600),BS2(800,-600),BS3(-800,-600),BS4(-800,600),其中,BS1设为主站,测量误差为3 m,监视点初始位置(0,0),移动监视点以匀速行驶,速度vx=vy=1 m/s,每2 s 估计1 次,估计50 次。
在加权最小二乘法、Chan 算法、Taylor 级数展开法、Friedlander 算法、SX 算法、SI 算法等6 种传统解算算法中,Taylor 级数展开法的定位性能最优[15],因此,只对传统解算方法中的Taylor 级数展开法进行仿真分析,门限值ε 设为0.1,仿真结果如图2 和图3所示。
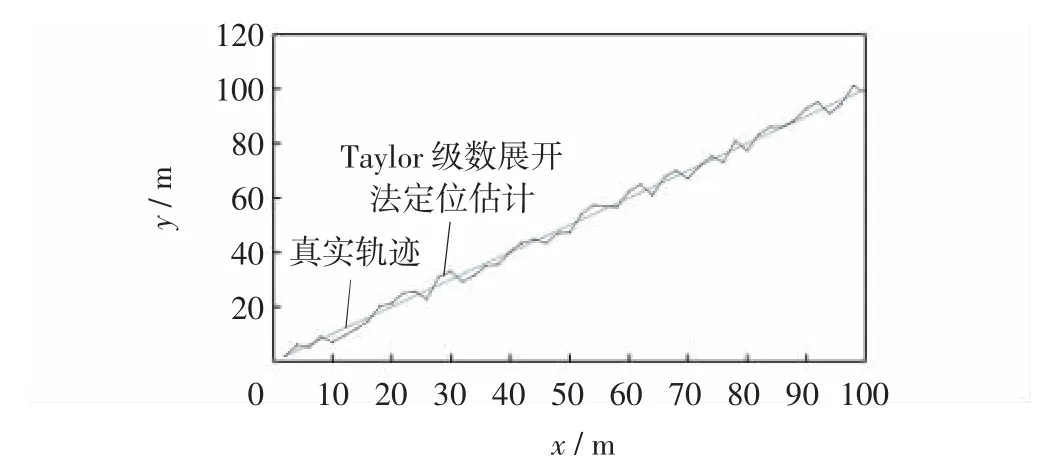
图2 Taylor 级数展开法定位估计与真实轨迹对比Fig.2 Comparison of Taylor algorithm positioning estimation and real trajectory
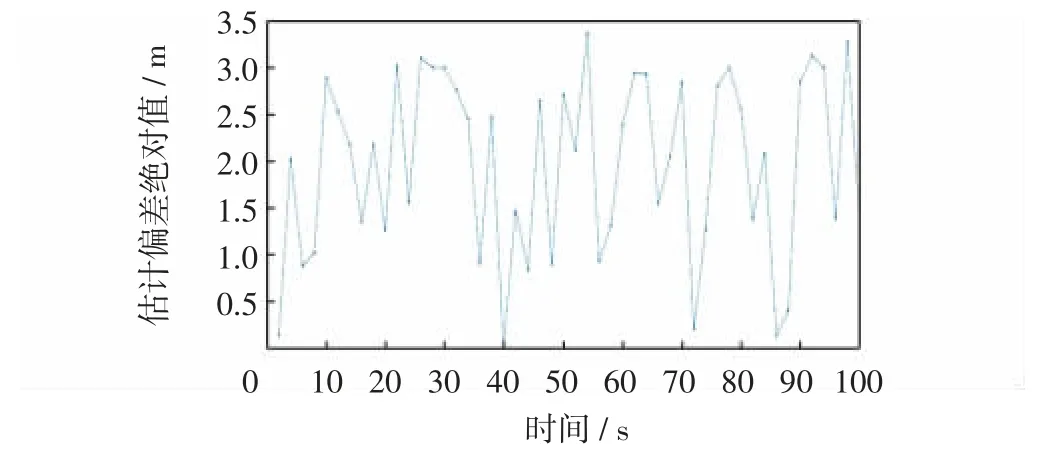
图3 Taylor 级数展开法定位估计与真实位置的偏差Fig.3 Deviation of Taylor algorithm positioning estimation from real position
图2 可看出,Taylor 级数展开法基本能对目标位置进行准确定位;由图3 仿真结果可知,Taylor 级数展开法定位估计与真实位置的偏差最大值为3.4 m。但Taylor 级数展开法的收敛速度及收敛性依赖于一个比较接近真实值的猜测初始值。
设置自适应弹射粒子群算法的参数:粒子群的种群规模M=30,最大迭代次数K=500,学习因子c1=c2=2,最大惯性因子ωmax=0.9 及最小惯性因子ωmin=0.3,小生境半径L=10 m,弹射速度常量v=(10,0)。标准粒子群算法、弹射粒子群算法、自适应弹射粒子群算法的优化仿真结果如图4所示。
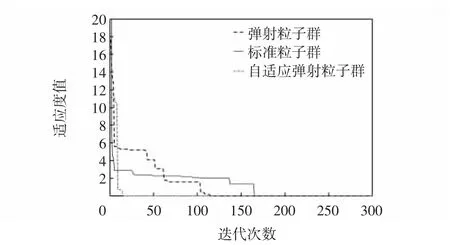
图4 3 种粒子群算法收敛图Fig.4 Convergence graph of three particle swarm algorithms
由图4 可看出,自适应弹射粒子群算法的收敛速度快、搜索精度高,避免“早熟”现象,更易找到全局最优解。
在上述仿真环境及自适应弹射粒子群算法的参数设置下,联合算法仿真结果如图5 和图6所示。

图5 联合算法定位估计与真实轨迹对比Fig.5 Comparison between joint algorithm positioning estimation and real trajectory
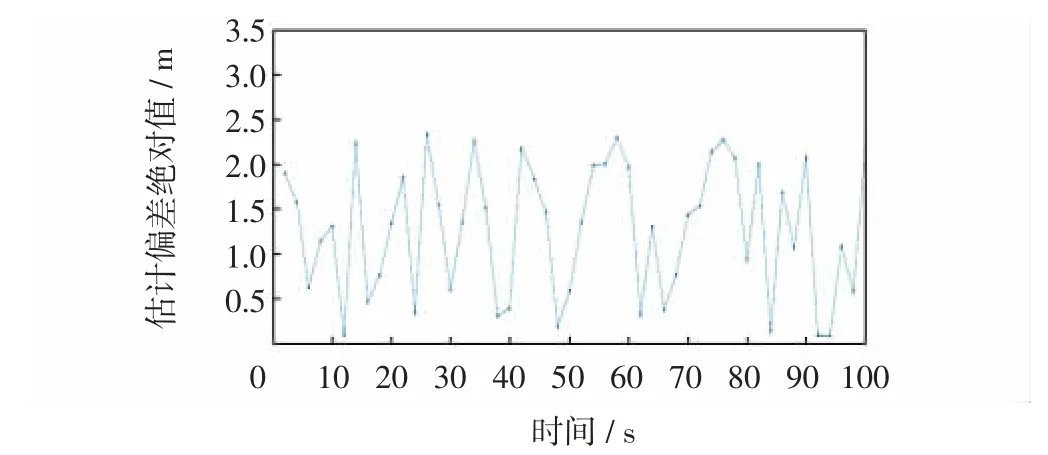
图6 联合算法定位估计与真实位置的偏差Fig.6 Deviation of joint algorithm positioning estimation from real position
由图5 联合算法定位估计与真实轨迹对比可看出,联合算法对真实轨迹的拟合程度要比Taylor 级数直接展开更高。图6 中联合算法定位估计与真实位置的偏差最大值为2.3,可看出利用自适应弹射粒子群算法得到一个接近真实位置的目标估计,再利用Taylor 级数展开法进行迭代,可有效减少定位估计与真实位置的偏差。
6 结语
随着国内外航空业的迅猛发展,多点定位系统作为一种新兴机场场面监视技术,得到了民航局的大力推广。利用对监视点的实时高精度可靠定位,有助于对机场场面进行运行调度,进而极大地提高机场场面的运行效率及航班准点率,减少机场场面安全事故。联合算法结合了改进的自适应弹射粒子群算法与Taylor 级数展开法,实现了对机场场面监视点的准确定位,具有一定的实用参考价值,但未考虑非视距情况下的定位影响因素,在今后的研究工作中还需做进一步讨论。

