航线网络中枢纽城市选择的多目标优化模型
樊 玮,宁俊文
(中国民航大学计算机科学与技术学院,天津 300300)
航线网络规划是航空公司运行控制的基础,对航空公司运营效率提升至关重要。城市对航线网络和枢纽航线网络是最常见的网络结构。从通达性和经济性两方面考虑,枢纽航线网络较城市航线对网络会增加飞行频率、通达性较差[1],但往往与经济、社会发展的规模强相关,可从整体上降低航空公司运营成本,因此,枢纽航线网络依然是中等以上规模航空公司的首选[2-3]。
枢纽网络结构分为p枢纽中值、无容量枢纽定位、p枢纽中位和枢纽覆盖4 种基本形式[4],基本思路都是基于航线网络可达城市集合,利用数学规划法选择有利于设定目标的枢纽城市集合[5-6]。常见的枢纽航线网络规划大都直接选取枢纽城市,也有少数研究根据城市属性(描述城市的性质与关系)、影响航线网络构造的因素(如机场运营效率、地理位置、机场服务水平等[7-8]),采用多属性决策方法选取候选枢纽城市集,但缺少对教育资源、城市生产总值、卫生状况等属性的考虑,而这些属性往往对航线旅客人数具有重要影响。另一方面,现有模型基本以总运输成本最小[9-11]或汇运和分运成本最小[12-14]为优化目标,很少有将二者综合考虑的模型。
在综合考虑机场运营效率、地理位置、机场服务水平的基础上,增加基于教育资源、城市生产总值、卫生状况得到的城市综合分值属性,在无容量限制的多分配p枢纽定位模型(Up)[13]基础上,建立以总运输成本、汇运和分运成本最小化为目标的多目标规划模型(UMp)。为了降低航线网络可达城市较多情况下模型求解的时间复杂度,实现航空运输利益最大化,首先,采用一种改进的淘汰选择算法[15]选取候选枢纽城市集,再用Cplex 软件对多目标优化模型进行分步求解。
1 城市候选集选取算法
相对于可达城市全集,采用候选枢纽城市集能较大幅度降低算法的时间复杂度。基于ELECTRE 算法构造一系列弱支配关系淘汰较劣方案,从而逐步缩小方案集直到选出满意的方案。首先,基于ELECTRE 算法进行候选城市筛选,算法计算步骤如下。
1)计算加权正规化评估值
定义可达城市集合M= {1,2,…,p},每个城市的属性集合N={1,2,…,q}。在M和N上构造原始评估矩阵A=(aij)p×q,元素aij为城市i的属性j的原始评估值,然后对所有元素aij进行正规化处理,即
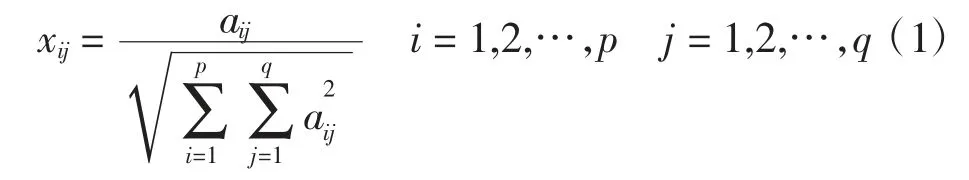
定义权重集合W={w1,w2,…,wq},其中wj为属性j的权重,再进行加权正规化处理,即

2)计算和谐集与非和谐集
根据可达城市集合中的每个城市对(k,l),将其属性集N划分为两个不相交的子集Okl和Ukl,其中:Okl为和谐集,由城市k不劣于城市l的属性组成;Ukl为非和谐集,由城市k劣于城市l的属性组成。两个不相交子集表示如下
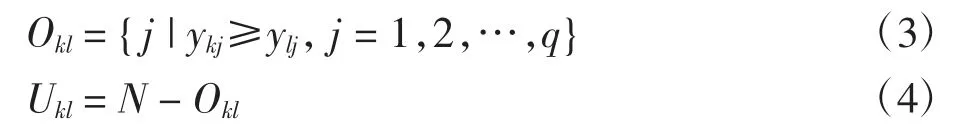
3)计算和谐矩阵与非和谐矩阵
和谐矩阵C=(ckl)p×p体现了两城市间的相对重要性,ckl值越高,表明城市k优于城市l的程度越大。非和谐矩阵D=(dkl)p×p反映了城市k劣于城市l的程度,dkl值越高,表明城市k劣于城市l的程度越大。C 和D的元素表示如下
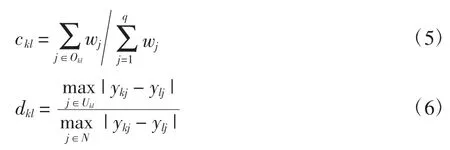
4)计算和谐超越矩阵与非和谐超越矩阵

式中
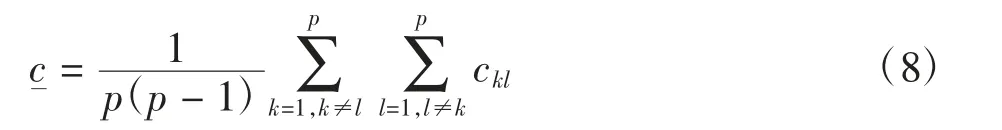

式中
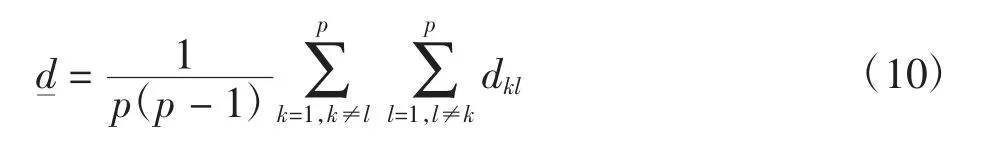
5)计算合计超越矩阵
合计超越矩阵E=(ekl)p×p是和谐与非和谐超越矩阵的交集,即ekl=fkl gkl,表示了城市选择的优先顺序,若ekl=1,则表示城市k在一致与非一致准则上均优于城市l。
最后,根据合计超越矩阵选择候选枢纽城市集L。
2 航线网络模型
从候选枢纽城市集中选出p个作为枢纽城市,模型中变量定义如下:
1)i,j代表城市节点;k,m代表候选城市节点;
2)vij为城市i到城市j的运输成本;qij为城市i到城市j的旅客需求量;dij为城市i到城市j的距离;
3)变量Xijkm为0-1 决策变量,当OD 流(i,j)经过枢纽城市k,m中转时为1,否则为0,其中,k和m可以相同;Hk是0-1 决策变量,当城市k是枢纽城市时为1,否则为0。
2.1 运输成本
枢纽航线网络的运输成本由汇运、转运、分运3 种成本组成,如图1所示。
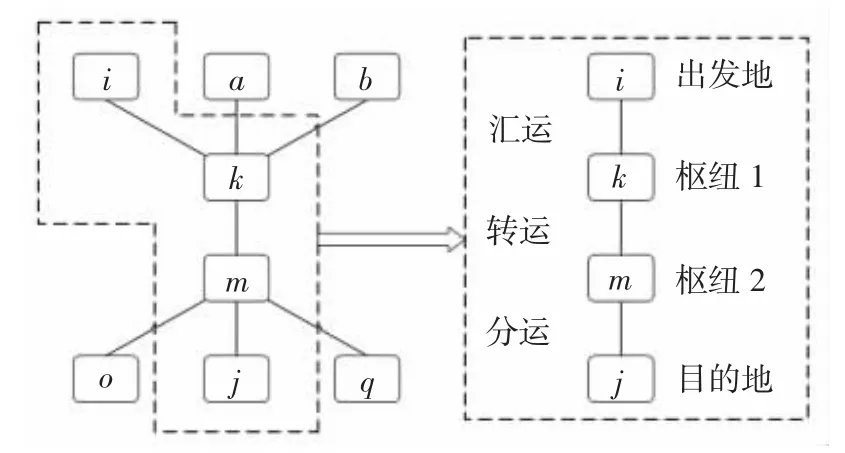
图1 3 种运输操作Fig.1 Three kinds of transportation operations
总运输成本定义为

式中x、a、b分别为汇运、转运、分运的折扣因子。一般情况下a <x,且x、a、b都小于1,a≠0,取x= 0.6,a=0.5,b=0.5。
汇运和分运成本之和定义为

2.2 枢纽城市选择模型
航线网络设计的首要目标是使航线成本最小化,但总运输成本与汇运和分运成本之间并非呈线性关系,因此,建立的UMp 模型采用多目标分层求解方式。
根据航空运输成本优先级关系,首先对总运输成本最小进行求解(式(13)),然后在此基础上求得汇运和分运成本最小的二次解(式(14)),最后综合总成本及汇运和分运成本再次求得最优解(式(15))。模型表示如下
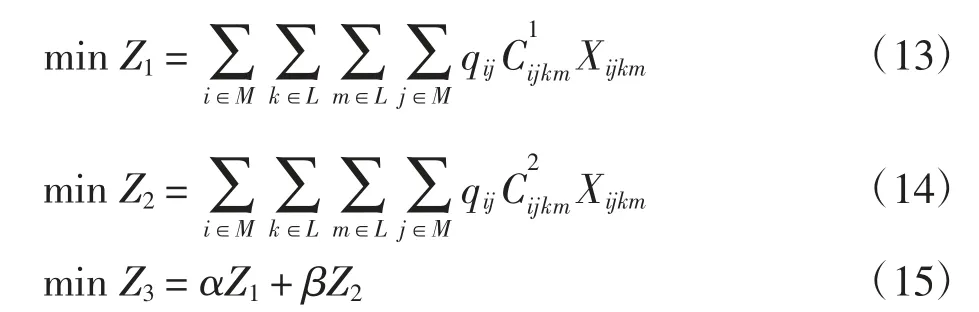
约束条件如下
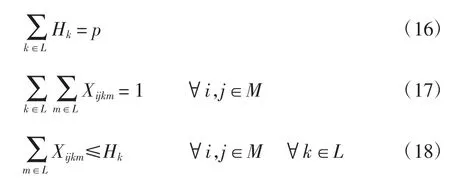
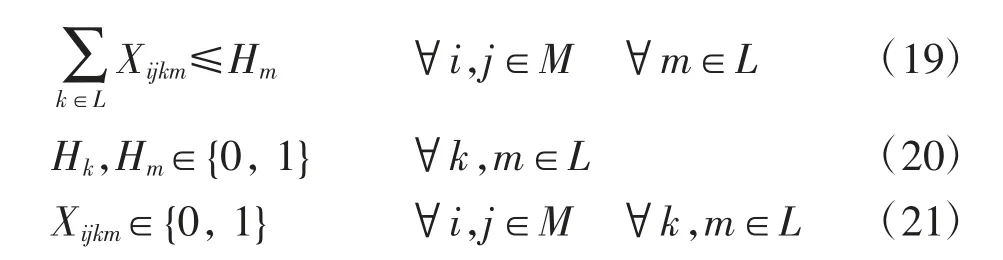
约束条件中:式(16)确保枢纽城市的个数为p;式(17)确保所有OD(origin destination)流的运量必须由起始城市运到目的城市;式(18)和式(19)保证了所有的OD 流只能通过枢纽城市进行中转运输。
3 实例分析
依据中国城市排行榜[16]获得国内20 个重要城市的地理位置和综合分值,依据中国民航资源网[17]获得对应机场的运营效率和服务水平,得到各属性的原始评估值;给定地理位置、综合分值、机场运营效率、机场服务水平构成的属性集N={1,2,3,4}所对应的权重集W={0.20,0.30,0.35,0.15},计算得到各城市的加权正则化属性值。如表1所示。
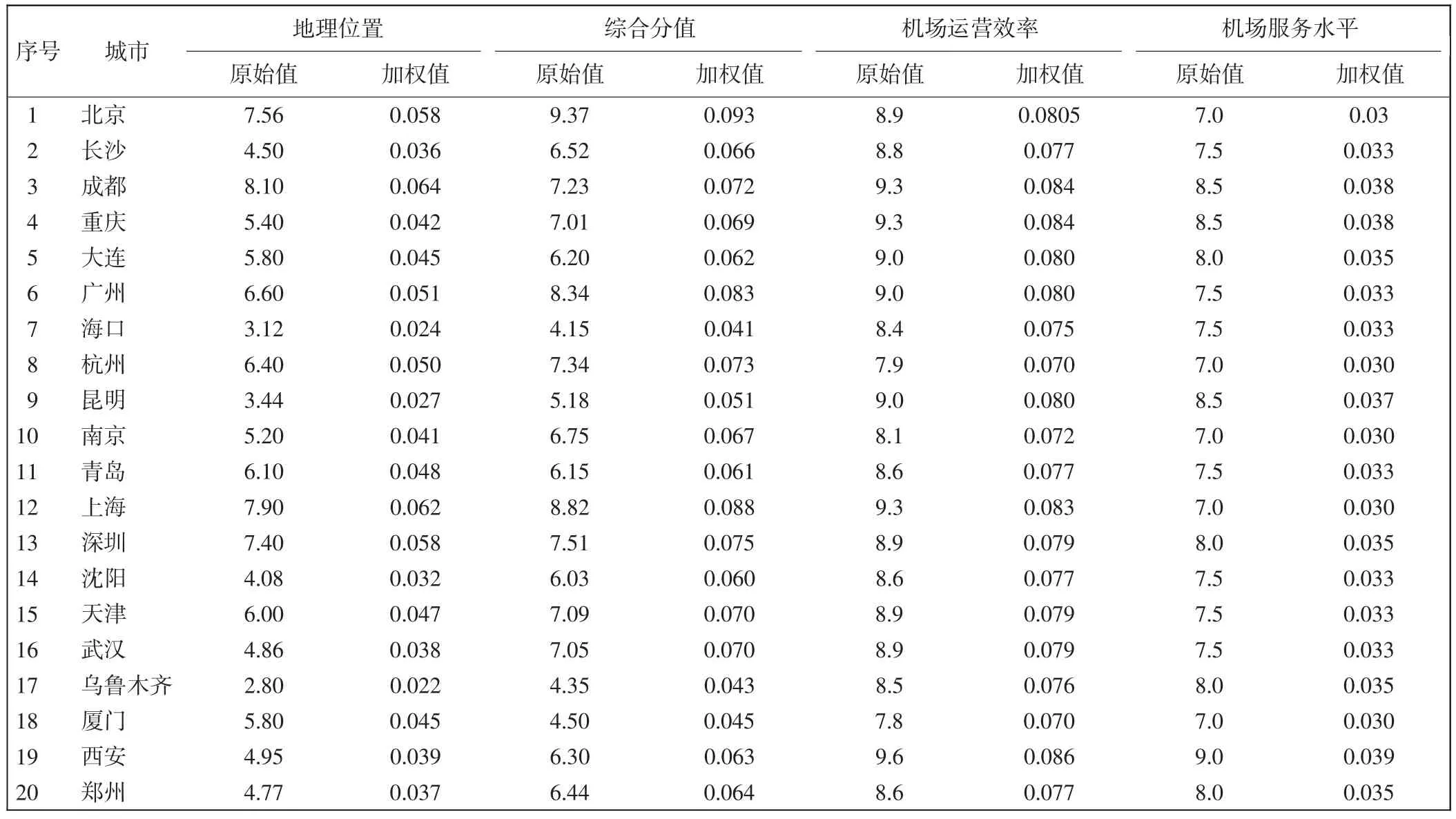
表1 城市各属性的原始评估值及加权正则化属性值Tab.1 Original value and weighted value of each attribute of city
根据加权正则化属性集构建和谐集与非和谐集,如表2 和表3所示(限于篇幅,仅列出部分城市)。从表2 和表3 中可得到O13={2},U13={1,3,4},表示北京的综合分值优于成都,但地理位置、机场运营效率、机场服务水平劣于成都。
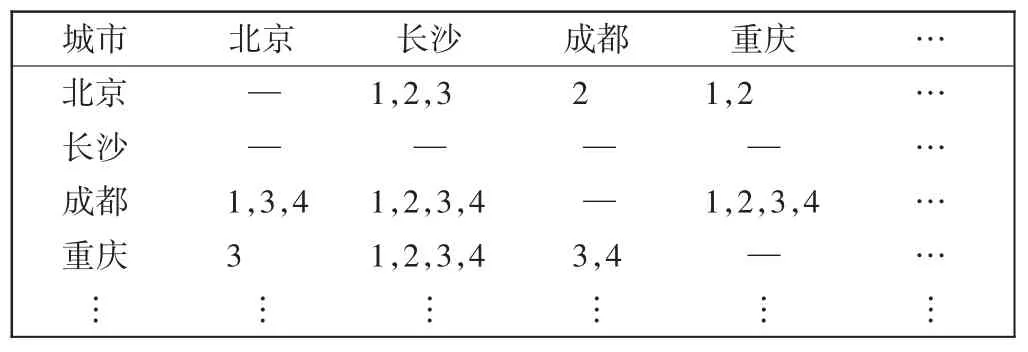
表2 城市和谐集Tab.2 Harmony set of city
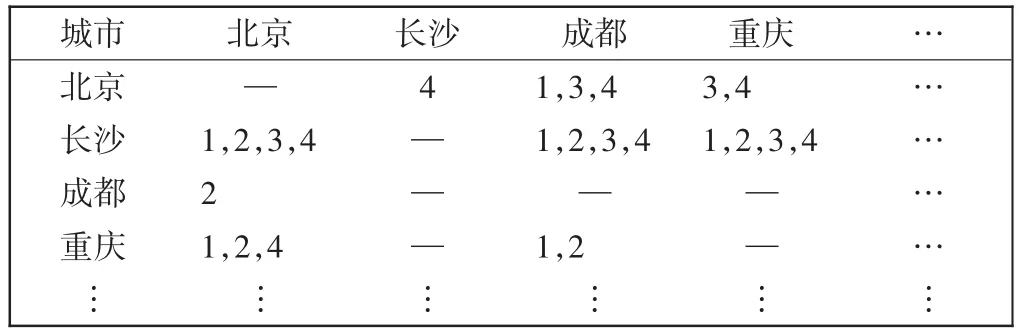
表3 城市非和谐集Tab.3 Inharmony set of city
据以上计算结果建立和谐矩阵与非和谐矩阵如下

如c13=0.30,d13=0.36,表示北京优于成都的程度较小,劣于成都的程度较大。
根据式(8)和式(10)求得门槛值和之后,求解和谐超越矩阵与非和谐超越矩阵,即
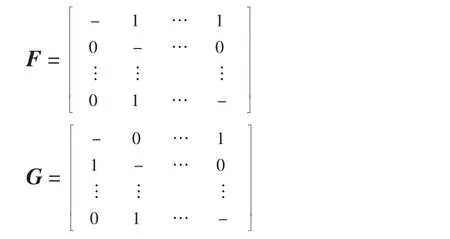
根据F 和G 构造城市合计超越矩阵E,如表4所示。
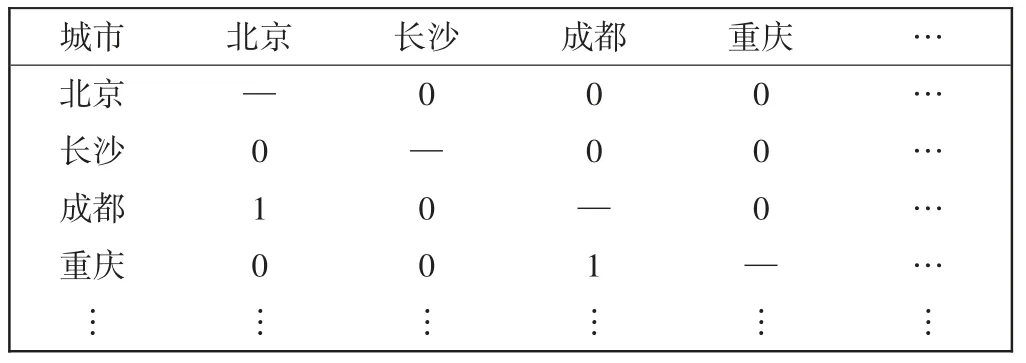
表4 城市合计超越矩阵Tab.4 Total exceeding matrix of city
为了更加直观表示城市的优劣,将表4 用偏序图(从左到右)表示,如图2所示。可选重庆、成都、北京、上海、广州、杭州、西安、深圳、沈阳、厦门等城市作为候选枢纽城市集L。
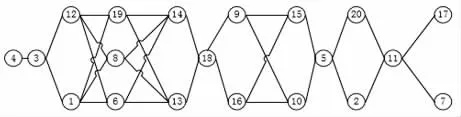
图2 城市优劣偏序图Fig.2 Pros and cons partial order map of city
采用15 个城市和20 个城市的场景进行模型验证,场景1 含有15 个城市(序号1、2、3、6、7、8、9、10、12、14、16、17、18、19、20),场景2 包含所有20 个城市,对场景1 经由表4 筛选排名前7 的候选枢纽城市,对场景2 经由表4 筛选排名前10 的候选枢纽城市。
依据varflight[18]网站提供的2019年1月—10月的航线网络数据,取α=1/4,β=3/4 来计算UMp 模型的总成本。指定枢纽城市数p=2~5,进行UMp 模型求解并与Up 模型进行对比。表5 为根据场景1 计算得到的结果,表6 为根据场景2 计算得到的结果。
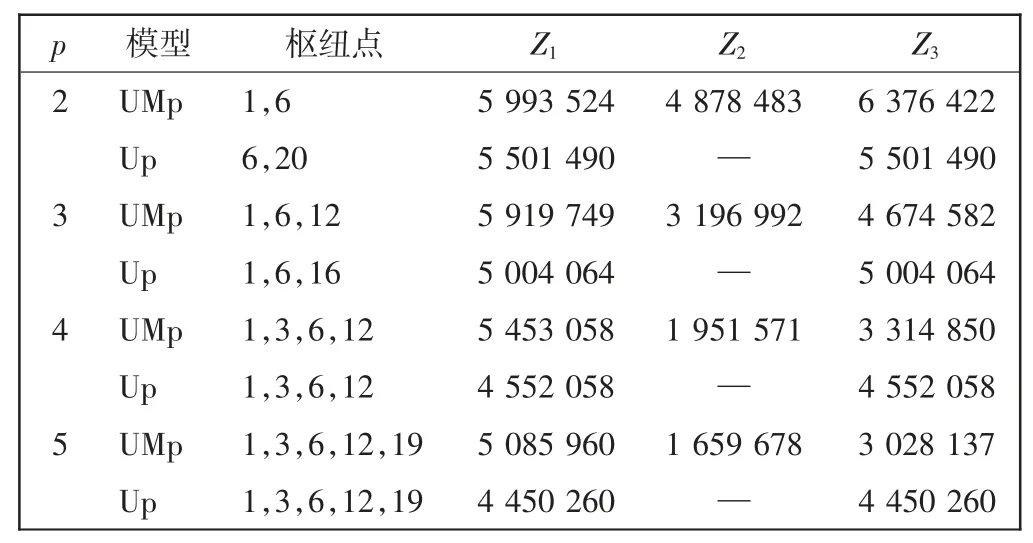
表5 场景1 中的计算结果Tab.5 Calculation results under scenario 1

表6 场景2 中的计算结果Tab.6 Calculation results under scenario 2
图3 和图4 分别为p=5 时场景1 和场景2 下UMp模型和Up 模型的航线网络图(红色点为枢纽点),表7为UMp 优先级稳定性的测试结果(优先级Z1>Z2>Z3)。
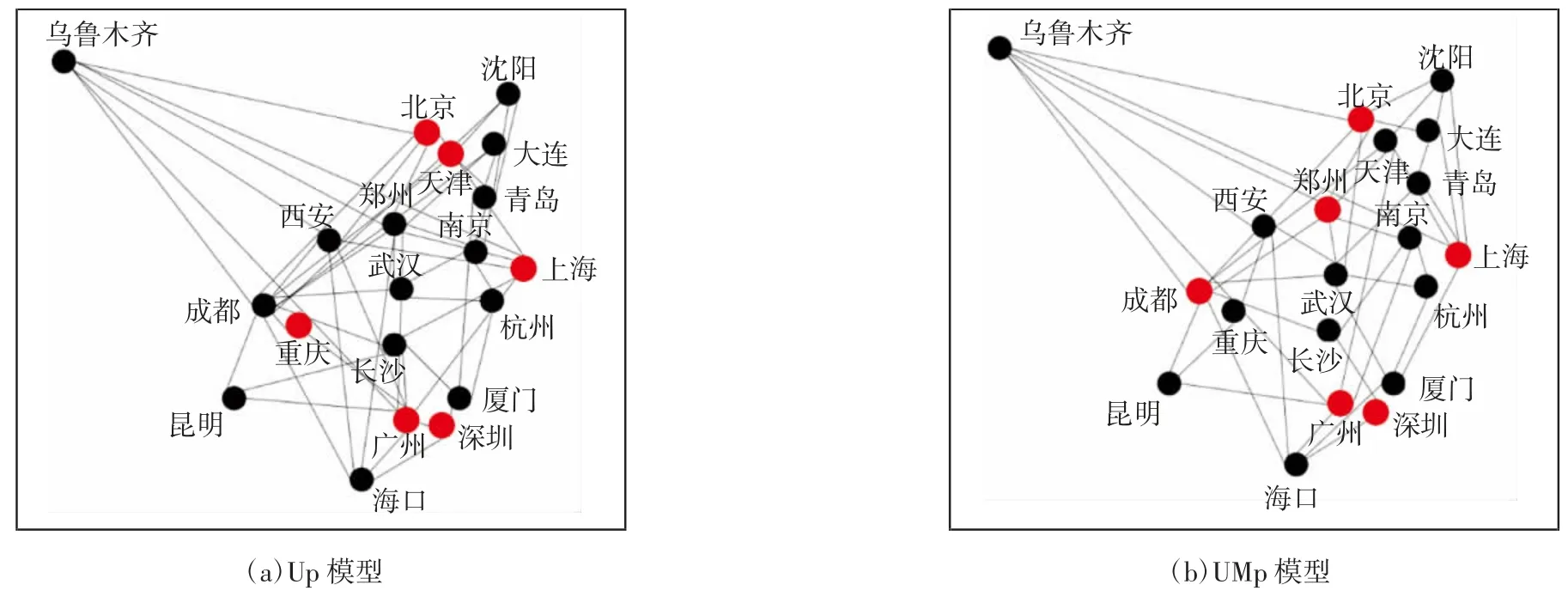
图4 场景2 下的航线网络图Fig.4 Route network connection diagram under scenario 2
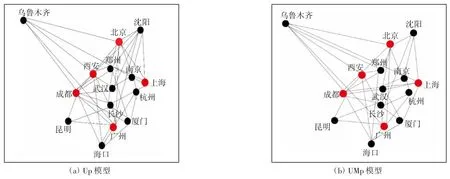
图3 场景1 下的航线网络图Fig.3 Route network connection diagram under scenario 1
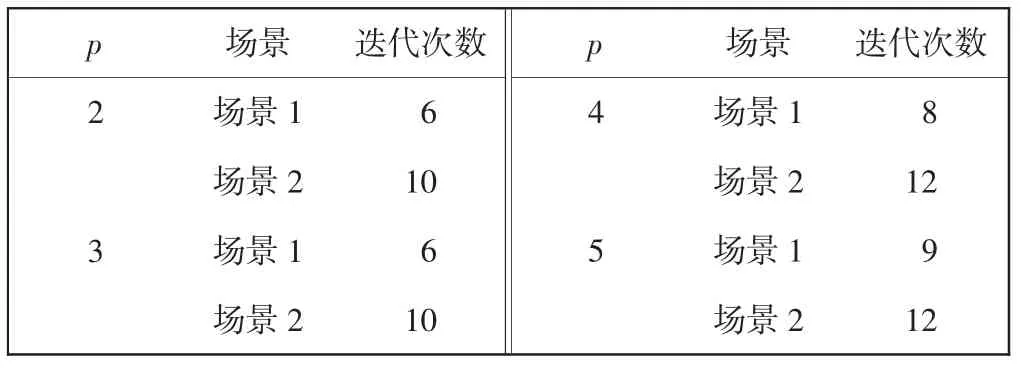
表7 UMp 优先级稳定性的测试结果Tab.7 Test results of UMp priority level stability 次
综上,对结果进行分析如下。
1)以二次优化后的最终总运输成本Z3进行比较:在场景1 下,p=2 时,UMp 劣于Up;p>2 时,UMp 明显优于Up;在场景2 下,p=2,3 时,UMp 劣于Up,p>3 时,UMp 明显优于Up。由此可见,UMp 模型适合用于城市规模较大、枢纽城市相对较多的情况,这也符合航空公司实际航线网络规划的情况。
2)在场景1 中,当p=4,5 时,UMp 和Up 所选枢纽城市一致,但UMp 的成本远低于Up。原因在于UMp 和Up 会给出不同的航线网络设计,图3 给出了p=5 时UMp 和Up 两种算法所得到的航线网络图。可见,在相同计算条件下,即使枢纽城市选择相同,UMp能给出更优的航线网络设计。
3)在场景2 中,UMp 和Up 所选的枢纽城市不一致,图4 给出了p=5 时的航线网络图,可看出枢纽城市的选取影响航线网络成本,UMp 模型能在相同规模下选取较优的枢纽城市,从而得到较优的结果。
4)为了检验UMp 结果的稳定性,进行了迭代次数检测。最多迭代次数为12 次,最少迭代次数为6 次,最终结果达到稳定,说明UMp 是稳定且可行的。
4 结语
针对航线网络枢纽城市选择的问题,提出了无容量限制的多分配p枢纽定位的多目标优化模型。该模型在综合考量可达城市的地理位置、综合分值、机场运营效率、机场服务水平4 个属性的基础上,采用ELECTRE算法选择了候选枢纽城市集,然后以总运输成本、汇运和分运成本、二次优化总运输成本最小为目标建立了枢纽城市选择多目标优化模型,最后,基于目标优先级迭代对模型求解,得到稳定的优化结果。
UMp 模型与传统Up 模型相比,适用于候选城市多且拟选择枢纽较多的情况,能在合理选择枢纽城市的基础上,设计优化的航线网络结构,有效降低航线网络的总运输成本,但未考虑枢纽城市的构建成本及航线的延误成本等因素,这可作为进一步的研究方向。

