空中交通流时间序列平稳性和非线性检验

王 飞

（中国民航大学空中交通管理学院，天津 300300）

空中交通系统是具有多实体、高动态、强耦合特点的复杂系统，基于线性系统的理论方法难以精确表征空中交通流的内在特征和动态演化规律，在交通流建模和预测领域面临着难以逾越的结构性缺陷，促使诸多学者应用非线性理论方法对空中交通系统内在动力学特征进行探索性研究，典型成果有：Li 等[1]应用小数据量法和小波去噪理论计算最大Lyapunov 指数，分析了飞行冲突时间序列的混沌特性；Cong 等[2]以扇区交通流量为对象建立时间序列数据，并研究其混沌特性；郑旭芳[3]和王超等[4]从混沌与分形角度对交通流量时间序列的非线性特征进行了研究；王飞[5-6]系统研究了空中交通流的分形特征，并基于Hurst 指数对空中交通流长相关性进行了实证分析。

以上成果均以空中交通流时间序列为研究对象，通过计算最大Lyapunov 指数、关联维数等特征指标，识别出空中交通流的混沌、分形特征，从而间接证实空中交通系统具有非线性。上述成果开启了空中交通流非线性研究的新途径，为流量短期预测提出了新思路，但仍存在如下不足：①特征指标对时序数据长度、噪声数据较为敏感，不同方法计算出的同一个指标结果有偏差，甚至互相矛盾，导致空中交通系统具有非线性特征的结论不具说服力；②特征指标的计算时间较长，不利于时间序列非线性的实时快速识别；③仅能判断观测数据是否包含非线性成分，但无法识别该非线性成分是来源于系统外部测量函数还是系统内在动力学过程本身；④上述方法都隐含“平稳时间序列”的前提条件，然而均未对观测数据的平稳性进行检验，平稳性检验是非线性检验的前提。

非线性是时间序列具有混沌或分形特征的必要条件，为了给应用非线性理论分析和预测空中交通流的合理性提供科学判据，有必要对空中交通流时间序列的非线性进行检验。只有当时间序列具有非线性，才能应用混沌或分形等非线性方法进一步研究。

表征空中交通流的指标有流量、速度、密度、机头距等，选择流量作为表征指标，一方面由于现有设备和技术手段较易获取流量数据，另一方面也为后续短期流量预测研究奠定基础。鉴于此，采集三亚4 号扇区连续40 d 的运行数据，根据需要构建不同流量的时间序列，研究其平稳性和非线性。

1 平稳性检验

严格意义上的平稳时间序列是指时间序列的所有统计性质不会随时间推移而变化，即其联合概率密度分布在任何时间间隔均相同。然而，实际系统产生的时间序列一般很难符合“严平稳”的要求，因此通常通过研究实测数据是否符合“宽平稳”要求来判定其平稳性。若一个时间序列{xk}是宽平稳时间序列，则具备以下性质：a）均值和方差均是与k无关的常数；b）自相关系数r（t）随着t增加快速下降，且趋近于0。自相关系数为

式中：xk表示时间序列第k个元素；xk+t表示第k+t个元素；表示时间序列数据的均值。

时间序列平稳性检验方法有两类：①基于图检验法的定性分析，即绘制时序图和自相关图进行直观判断；②基于单位根检验的定量分析，主要有ADF（augmented Dickey-Fuller test）检验和PP（Phillips-Perron）检验。选取连续40 d 的数据，以15 min 为统计间隔，构建交通流量的时间序列（共3 840 个数据），对其平稳性进行定性和定量分析。

1.1 定性分析

空中交通流量时间序列的时序图如图1所示。可以看出，当k取不同值时，时序数据都围绕一个水平均值线（图1 中白色线条）上下波动，且以相近似的发散程度分布，说明其均值和方差均是与k无关的常数，符合宽平稳时间序列性质a）。

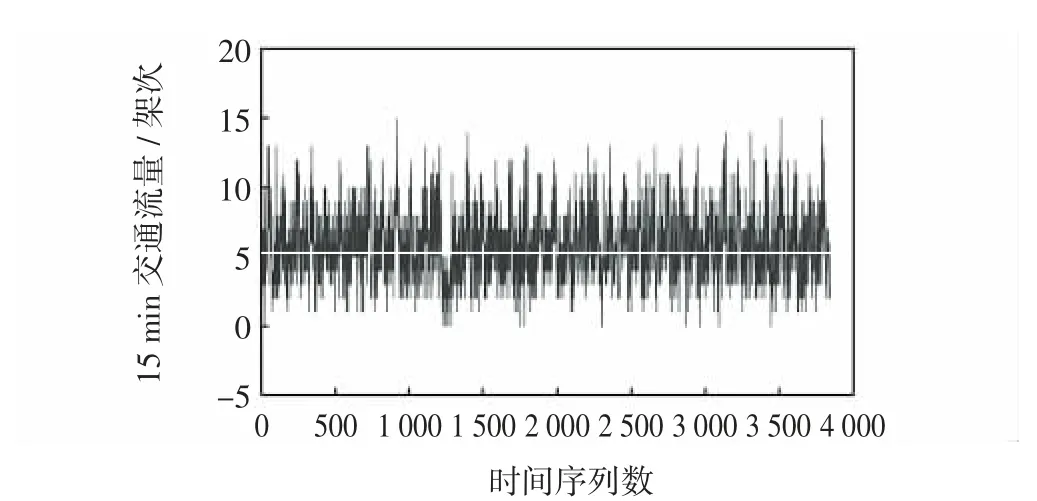
图1 空中交通流量时序图Fig.1 Time series diagram of air traffic flow

空中交通流量时间序列自相关图如图2所示。可以看出，随着t增加，自相关系数整体呈现快速下降趋势，并逐步趋近于0，符合宽平稳时间序列性质b）。

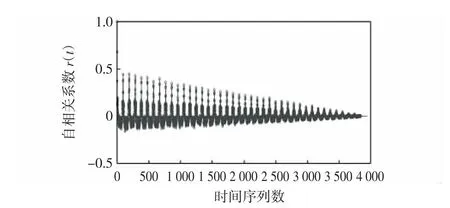
图2 空中交通流量时间序列自相关图Fig.2 Time series autocorrelation diagram of air traffic flow

1.2 定量分析

时序数据平稳性检验关键在于判断时序生成过程中是否存在单位根，因此常称为单位根检验。若时间序列平稳，则数据生成过程中不存在单位根。目前常用的单位根检验方法是ADF 检验和PP 检验，ADF检验对生成数据的自回归模型参数进行估计，PP 检验则采用非参数估计方法[7]，利用Matlab 中的adftest 和pptest 函数对时间序列进行平稳性检验，结果如表1所示。可以看出，无论采用AR 还是ARD 作为数据生成模型，无论显著性水平是0.05 还是0.01，ADF 和PP 检验结果都是平稳的。

表1 时间序列平稳性定量分析Tab.1 Quantitative analysis of time series stationarity

定性、定量分析结果一致，说明本部分构建的空中交通流时间序列是平稳的，可以在此基础上对平稳时间序列进行非线性检验。

2 非线性检验

时间序列的非线性检验方法主要分为模型检验法和替代数据法两大类[8]。模型检验法的基本思想是：分别应用线性模型和非线性模型对时间序列进行建模，若基于非线性模型的建模误差明显小于线性模型，则说明时间序列含有非线性成分。由于实际数据往往难以用解析模型进行精确建模，且不易选择合适的模型参数，因此模型检验法应用局限性较大。Theiler 等[9]提出了适应性更为广泛的替代数据法，其基本思想是：以某些线性过程为零假设，并根据零假设生成一组能够保持原时间序列数据线性特征的替代数据，分别计算原始数据和替代数据的统计检验量，如果两者有显著差别，则拒绝零假设，说明原始时间序列不太可能从与零假设一致的系统中产生，即原始时间序列存在非线性成分。

替代数据法可进行时间序列的非线性检验。该方法本质上是一种统计假设检验，包括3 部分：零假设、生成替代数据和计算检验统计量。

2.1 零假设

零假设是对原始时间序列特征的一种假设性猜测，其作用是提供替代数据的生成依据。文献[9-10]提出了3 种零假设，并沿用至今，成为目前最具代表性的零假设。具体描述如下。

零假设1替代数据由独立同分布的线性随机过程产生。拒绝该假设，说明原始序列并非是独立的，可能具有线性或非线性相关性，需要进一步检验。

零假设2替代数据由具有原始数据均值和方差的线性高斯过程产生。拒绝该假设，说明原始数据具有非线性成分，但无法明确该非线性成分的来源。

零假设3替代数据由线性相关高斯噪声经过静态、非线性变换产生。拒绝该假设，说明原始数据的非线性成分并非来自系统外部，而是来自系统自身的动力学过程。

这3 个零假设体现了不同的线性过程产生机理，后续将逐一检验。

2.2 生成替代数据

替代数据生成方法分为传统实现法和受限实现法[11]。传统实现法主要通过AR、ARMA 等线性模型生成替代数据，虽然该方法在计算置信区间方面效果明显，但针对源自实际系统时间序列的数学建模缺乏经验模型。受限实现法无需数学建模，从时间序列本身出发，通过变换顺序、相位等操作即可获得替代数据。以下采用受限实现方法生成替代数据。

根据不同的零假设，生成满足零假设的替代数据算法是不同的，下面分别进行说明。

2.2.1 针对零假设1

基于零假设1，生成的替代数据应保持原始数据的线性特征，如均值、方差、幅值等，生成方法较为简单，只需打乱原始序列元素顺序即可得到替代数据。

2.2.2 针对零假设2

基于零假设2，生成的替代数据应保持原始数据的线性特征，如均值、方差、功率谱等，可采用傅里叶变换FT（Fourier transform）算法生成替代数据。FT 算法首先将原始数据进行傅里叶变换，然后保持功率谱增幅不变，将功率谱中各频率成分的相位随机化，最后进行傅里叶逆变换即可获得替代数据。FT 算法的优点是产生的数据特征比较稳定，通过重构原始数据的功率谱以保证替代数据同原始数据的线性相关性。FT适用于平稳时序数据，具体步骤如下：

步骤1通过傅里叶变换，将原始时间序列X={xk}变换为序列A={ak}；

步骤2随机生成新的功率谱相位序列F={fk}，k=1，2，…，n，其中n表示原始序列长度，fk∈[-π，π]；

步骤3当n为偶数时，fk重新赋值方式如下

当n为奇数时，fk的重新赋值如下

步骤4对时间序列A 按照式（4）进行相位随机化处理，构建新时间序列B={bk}，即

式中i表示虚部。

步骤5将B 按照式（5）进行逆傅里叶变换得到新的时间序列Y={yk}作为替代数据，即

式中：i 表示虚部；j表示变量。

需要说明的是，在步骤2 中，有学者考虑在[0，2π]范围内随机取值[12]，但这并不能保证替代数据Y 一定为实数，因此采用fk∈[-π，π]的取值范围[13]。至此可生成一条替代数据，根据需要重复步骤2 至步骤5 即可获得多条替代数据。该算法产生的替代数据的时间概率分布为正态分布，当原始数据不服从正态分布时，不宜采用该算法[14]。而大部分实际系统产生的数据，尤其是短序列数据，并不满足正态分布的要求，因此需谨慎使用该算法产生替代数据。

2.2.3 针对零假设3

零假设3 的替代数据一般采用幅值调整傅里叶变换算法（AAFT,amplitude adjusted Fourier transform algorithm）生成。该算法首先使原始数据服从正态分布，然后按照FT 算法产生替代数据，最后再使替代数据服从原始数据的分布。该算法可以绝对保证替代数据与原数据有相同的时间概率分布，同时使其功率谱密度较为接近，原序列无需满足正态分布。AAFT 算法适用于平稳时序数据，具体步骤[15]如下：

步骤1随机生成一组高斯分布G={gk}；

步骤2按照原始时间序列X={xk}的秩重新排列G，得到新的序列A，这样得到的时间序列A 既遵循原始数据的排列顺序又具有高斯型幅值分布形式；

步骤3按照FT 算法生成序列A 的替代数据B；

步骤4按照B 的秩重新排列原始序列X，得到最终的替代数据Y。

重复步骤1 至步骤4 可获得多条替代数据。替代数据与原始序列幅值分布形式一致，能够反映原始序列的静态、单调非线性性质，同时，又具有相同的功率谱，原序列的线性相关性被隐含在产生替代数据的过程中。

2.3 计算统计检验量

检验统计量直接影响判别结果的优劣。由于没有先验经验，所构建的时间序列是否具有非线性及非线性强弱都是未知的，因此应当选择能够检验出弱非线性的统计量。诸多学者提出了许多用以区分线性系统和非线性系统的检验统计量，如基于关联积分函数的BDS（Brock-Dechert-Scheinkman）统计量[16]、基于信息论的熵统计量[17]、基于分形维数的统计量[18]，但计算量大且对于短序列、弱非线性检验效果不理想。

时间可逆性是区分线性与非线性系统的基本特征，源自线性系统的时序数据在时间反转下总是对称的，而非线性系统则不然。三阶时间逆不对称性统计量Q（τ）能有效识别时间可逆性，三阶自相关统计量T（τ1，τ2）和三阶自协方差统计量C（τ1，τ2）能够较好地检验出系统的弱非线性成分，计算过程如式（6）～式（8）所示。

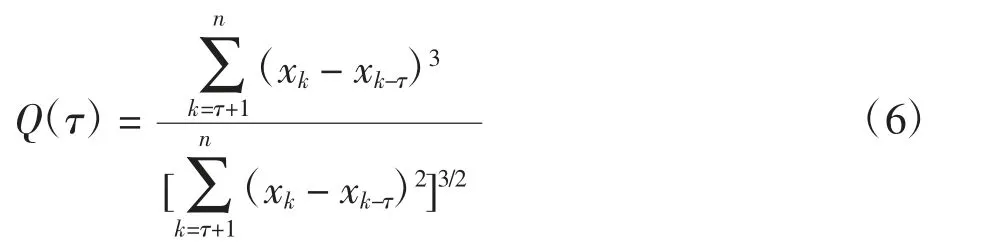
式中：τ 表示时间延迟；xk表示时间序列第k个数值；n表示时间序列长度。

式中τ1、τ2表示时间延迟，一般取τ2=2τ1。

通常采用Sigma 检验方法对原始数据和替代数据的检验统计量进行分析。假设原始数据的三阶自相关统计量为T0，其替代数据的三阶自相关统计量均值为TS、均方差为σS，则Sigma 检验量S计算方法为

根据Sigma 检验原则，在显著性水平0.05 下，当S≥1.96 时，拒绝原假设，说明原始序列具有非线性成分。

2.4 非线性检验结果

采用时间逆不对称性三阶统计量Q（τ）、三阶自相关统计量T（τ1，τ2）和三阶自协方差统计量C（τ1，τ2）对3 种零假设进行检验。由于零假设2 的检验需要原始数据满足正态分布，零假设1 和零假设3 对于原数据的分布没有特殊要求，因此首先进行原数据的正态性检验。

2.4.1 正态性检验

正态性检验方法很多，JB（Jarque-Bera）检验、KS（Kolmogorov-Smirnov）检验和Lilliefors 检验的适用条件虽然有些许差异，但均能用于一般的正态性检验。显著性水平设置为0.05，应用Matlab 中相关检验函数，3 种检验方法得到的结果均拒绝原假设，说明原始时序数据不服从正态分布。

2.4.2 非线性检验

显著性水平设置为0.05，应用蒙特卡洛方法产生1 000 组替代数据，按照式（9）计算的Sigma 检验量结果如表2所示。

表2 Sigma 检验量计算结果Tab.2 Calculation results of Sigma test quantity

可以看出，3 种检验量均拒绝了零假设1 和零假设3，说明原时间序列具有非线性成分，且来源于系统自身动力学过程，后续可尝试应用混沌、分形等非线性方法进行演化机理和短期预测研究。Q（τ）、T（τ1，τ2）接受零假设2，C（τ1，τ2）拒绝零假设2，验证了非正态分布数据会造成零假设2 检验结果的不确定性。

3 影响因素分析

3.1 时序长度影响分析

流量时间序列非线性分析的最终目的是流量短期预测，因此对实时性有较高要求。从第1 d 96 个数据开始，逐天滚动增加96 个数据，直到第60 d 数据更新完毕，以零假设3 为例，取τ=τ1=5，Q（τ）、T（τ1，τ2）和C（τ1，τ2）随时序长度的变化趋势如图3～图5所示。

图3 Q（τ）随着时序长度变化趋势Fig.3 Q（τ）vs.time series length

图4 T（τ1，τ2）随着时序长度变化趋势Fig.4 T（τ1，τ2）vs.time series length

图5 C（τ1，τ2）随着时序长度变化趋势Fig.5 C（τ1，τ2）vs.time series length

可以看出，针对同一个时间序列，尤其是短时间序列，3 种检验统计量的检验结果并不一致。Q（τ）从第35 d（3 360 个数据）之后，数值保持在1.96 之上，说明时间序列保持稳定的非线性；T（τ1，τ2）从第3 d（288个数据）之后，时间序列保持稳定的非线性；C（τ1，τ2）数值始终大于1.96，时间序列从第1 d 就保持稳定的非线性。综合上述结果，可以确定长度在3 360 以上的时序是非线性的，长度在3 360 以下的时序尚不能确定是否具有非线性。

需要说明的是，当使用60 d 时序数据（5 760 个数据）时，生成替代数据和计算3 种检验统计量的时间均在60 s 以内，计算效率高，满足实时性要求。

3.2 时间延迟影响分析

时间延迟是计算检验统计量的重要参数，需要对其影响进行分析。以零假设3 和40 d 的时序数据为例，设τ1或τ2从1 逐步增加至100，Q（τ）、T（τ1，τ2）和C（τ1，τ2）的变化趋势如图6～图8所示。

从图6～图8 中可以看出，随着τ 的增加，Q（τ）在1.96 上下浮动，并不稳定，说明Q（τ）受τ 影响较大；随着τ1的增加，T（τ1，τ2）和C（τ1，τ2）的变化趋势大体相同，大部分取值大于1.96，说明T（τ1，τ2）和C（τ1，τ2）受τ1影响不大。

图6 Q（τ）随时间延迟τ 变化趋势Fig.6 Q（τ）vs.time delay τ

图7 T（τ1，τ2）随时间延迟τ1 变化趋势Fig.7 T（τ1，τ2）vs.time delay τ1

图8 C（τ1，τ2）随时间延迟τ1 变化趋势Fig.8 C（τ1，τ2）vs.time delay τ1

3.3 统计尺度影响分析

不同统计尺度所构造的时序数据的非线性是不一样的，如果统计尺度过大，时序数据往往体现出宏观层面统计意义上的均值，掩盖了系统微观层面内在的动力学特征，如果统计尺度过小，时序数据体现不出空中交通流量的实际物理意义。以30 min、60 min为统计尺度，对60 d 数据重新构造时间序列，并与原15 min 尺度的时间序列进行对比分析，取τ=τ1=5，结果如图9～图11所示。

图9 不同统计尺度的Q（τ）变化趋势Fig.9 Variation trends of Q（τ）in different statistical scales

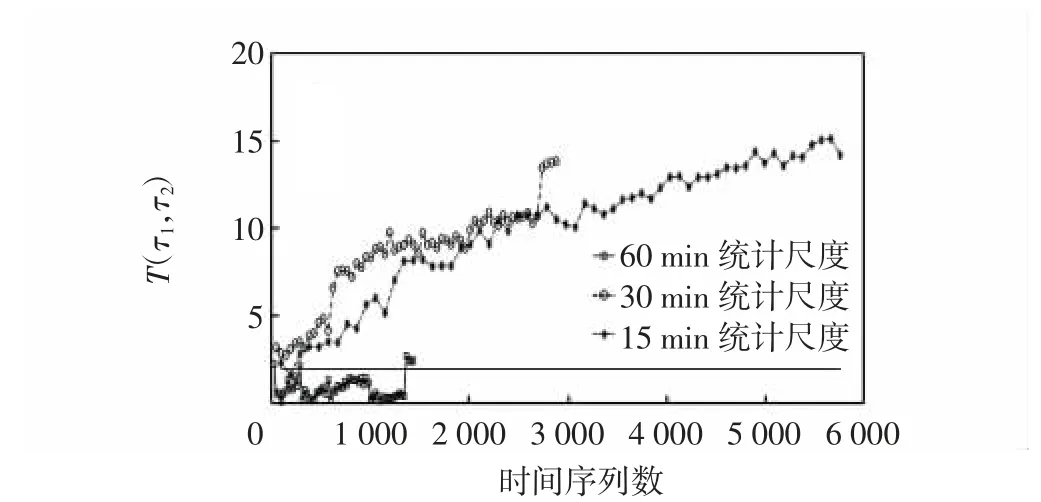
图10 不同统计尺度的T（τ1，τ2）变化趋势Fig.10 Variation trends of T（τ1，τ2）in different statistical scales

图11 不同统计尺度的C（τ1，τ2）变化趋势Fig.11 Variation trends of C（τ1，τ2）in different statistical scales

从图9～图11 中可以看出：考虑Q（τ）统计量时，30 min、60 min 尺度的时间序列只需要少量数据即可判断出较为稳定的非线性；考虑T（τ1，τ2）和C（τ1，τ2）统计量时，30 min、15 min 尺度的时间序列只需少量数据即可判断出较为稳定的非线性，而60 min 尺度的时序显示为线性。因此，从实际应用出发，30 min 尺度的空中交通流量时间序列更适用于三亚4 号扇区流量的短期预测。

4 结语

针对三亚4 号扇区的空中交通流时间序列进行了平稳性和非线性检验，得出以下结论。

1）并非所有时间序列都具有非线性，在应用非线性方法研究时间序列之前需进行非线性检验。替代数据法是一种有效的非线性检验方法。

2）所采用的空中交通流量时间序列具有非线性成分，且该非线性成分源自系统动力学本身。

3）时序长度、时间延迟和统计尺度对Q（τ）、T（τ1，τ2）和C（τ1，τ2）等非线性统计量有不同程度的影响。

4）针对三亚4 号扇区运行情况，30 min 尺度的空中交通流量时间序列只需少量数据即可体现出稳定的非线性，可采用非线性方法进行流量的短期预测。