核主成分-k近邻算法在心脏疾病分类中的应用研究

胡 扬，魏毅强

据世界卫生组织统计，目前全球范围内包含心血管疾病在内的心脏病导致每年死亡人数将近2 000万人，由国家心血管病中心组织编撰的《中国心血管病报告 2018》(2019年4月)指出：我国心血管病患病率持续上升，心血管病现患人数推测有2.9亿人。心血管病死亡率仍居首位，高于肿瘤及其他疾病，每5例中就有2例死于心血管病，且农村死亡率高于城市。同时更令人担忧的是发病年龄也呈现出年轻化的趋势，形势非常严峻。诱发心脏病的风险因素很多，包括心脏病家族史、吸烟、胆固醇、高血压、肥胖和缺乏锻炼等，而治疗该类疾病最好的方法是预防，关键在于早发现、早诊断和早治疗。如何有效预防心脏病，对潜在患病人群进行准确检查诊疗，具有重要的理论和现实意义。

近年来，随着信息与大数据技术的应用，使得数理医学在疾病诊断与预测领域取得了长足的进步和飞速的发展。在数据处理方面，很多学者都采用核主成分分析(KPCA)方法对数据进行核变换及降维，Deng等[1]提出了一种增强的KPCA方法，从而可以更好地挖掘数据的信息；Chen等[2]通过KPCA提取数据主要特征进行降维；Long等[3]通过KPCA提取缺陷的主要特征使得分类效果明显提升；Xie 等[4]处理高维数据时使用了KPCA来降维。在疾病分类方面，Fan等[5]将KPCA与AdaBoost等算法结合提高了阿尔茨海默病病人的分类正确率；Choi等[6]通过卷积神经网络对大脑磁共振图像进行分析，从而对老年痴呆症病人进行分类；Shankar等[7]用多核向量机提高了甲状腺疾病分类的准确率和灵敏度；Tufail等[8]构建了多个深度二维卷积神经网络，从局部大脑图像中学习不同的特征，并结合这些特征进行最终分类，用于阿尔茨海默病的诊断。Deng等[9]基于改进的Mel-frequency倒谱系数特征和卷积递归神经网络对心音进行分类；Chen等[10]通过改进的频率小波变换和卷积神经网络对心音进行高效分类；Yang等[11]通过决策树、随机森林和人工神经网络方法对主动脉狭窄进行分类；Soares等[12]提出了一种新的扩展零阶自主学习多模型神经模糊方法，可以通过心音对不同的心脏疾病进行分类；Tang等[13]使用旋转线性核支持向量机分类器对心律失常进行分类；Wang等[14]提出了对偶全连接神经网络模型来对心律进行精确分类；Wang等[15]对心律失常的分类也提出了一种改进的卷积神经网络模型并得到了很好的结果；Bzl等[16]不仅提出了一种新的基于深度剩余网络的心律失常深度学习分类方法，还使用二联导心电信号结合深度学习方法来自动识别5种不同类型的心跳。以上研究虽然对心脏疾病的诊断和分类有不少帮助，但由于心脏数据的复杂性、特殊性、高度非线性等因素导致对于疾病的准确判断比较困难。

本研究以描述心脏单质子发射计算机断层扫描数据集为基础，该数据集有267个病人样本，每个样本有44个连续特征模式并被分为正常和异常。但由于数据非线性而且维数较高，给正确分类造成很大困难和影响。本研究通过核主成分将数据集进行核变换和降维，从而去掉非线性影响并降低分类难度，经过核变换后的数据集进行正态分布检验。由于高斯径向基的参数难以选定，本研究采用非参数统计中的Friedman秩方差分析法对参数的取值进行了检验，并最终选择了最合适的参数值。选定参数值后，在此基础上选用k近邻(KNN)分类方法对267例病人进行分类，并与未进行核变换的主成分分析-k近邻(PCA-KNN)方法比较结果，可以看出本研究提出的方法得到了较好的性能提升。

1 核主成分分析

1.1 主成分分析 信息维数过高是处理多特征数据最大的挑战之一，多数情况下不同特征变量之间都具有一定的相关性。主成分分析是一种最为常见的数据降维方法，它可以将大量具有相关性的变量线性组合成一些不相关的新变量，同时还能尽可能保留原始数据集的大部分信息，这些新变量就叫做主成分。主成分分析的应用十分广泛，比如人脸识别、声音识别、综合评价等。通过主成分分析，可以简化问题的处理难度，并且提高工作效率。

1.2 核主成分分析 主成分分析仅仅是原始特征变量的线性组合，适用于具有线性特征的数据集，在处理非线性问题时往往不能达到很好的效果，而核主成分分析可以较好地对非线性问题进行线性化并降维。KPCA将输入空间中的数据通过映射φ映射到高维特征空间中，使映射后的数据集在高维特征空间中是线性可分的。核主成分牺牲的是维度，通过不同的核函数进行映射，再对特征降维，进行主成分分析。

常用的核函数有以下3种：

①q阶多项式核函数

K(Ai,Aj)=[(Ai,Aj)+1]q

②线性核函数

K(Ai,Aj)=(Ai,Aj)

③高斯径向基(RBF)核函数

KPCA实现的优良程度取决于核函数的选取。多项式核函数适用于图像处理，线性核函数适用于线性可分且特征数量较多的情况，高斯核函数是最常用的核函数，具有良好的局部特征提取能力和平滑特性。本研究选取的是高斯径向基核函数(RBF)。

将原始数据空间变换为特征空间，并在特征空间中对数据进行主成分分析，本研究中仅选取第一次贡献率达到97%的主成分个数。

2 k近邻方法

k近邻方法是有监督的机器学习分类算法之一[17-19]。在k近邻方法中，事先确定k值、距离度量等并提前准备好训练集及测试集，通过训练集把特征空间划分成一些子空间，训练集中的每个样本占据其中一部分空间。当k=1时，是k近邻的特殊情况，也被称为最近邻。在最近邻中，当测试样本落在某个训练样本的子空间内时，该测试样本就划分为这个训练样本所属的类别。 当k>1时，给定训练数据集X，对于测试数据Y，在X中找到与之距离最近的k个样本，在这k个样本中，若大部分样本属于某一类S，则将Y归为S类。最常用的距离度量是欧式距离，也有Manhatan距离，Minkowski距离等。

k值的选择十分重要，会对其分类结果产生重要影响。k值选择较小，则整体分类模型就会变得更加复杂，容易产生过拟合现象；k值选择较大，整体分类模型会过于简单，分类结果正确率容易降低。k值的选择一般为奇数，避免出现无法判断的情况。通过在训练数据集上的分类结果正确率显示，k=3时分类效果最好，因此，本研究中选取k=3。

3 Friedman秩方差分析法

设一共有t个处理和b个区组，首先在每1个区组内排秩，得到表1。

表1 完全随机区组秩排序表(Rij)

其中Rij为第i个处理中第j个区组的秩。

进行假设检验：

H0：各个处理中无差异；

H1：各个处理中有差异。Friedman统计量为：

(1)

(2)

Friedman检验依赖于每个区组内所排列的秩的大小，对试验误差没有正态分布的要求。

4 实例分析

本研究选取了描述心脏单质子发射计算机断层扫描的SPECIF数据集，该数据集有267个病人样本，每个病人有44个连续特征变量，并被分为两类：正常和异常。从中选取部分作为训练集，余下的作为测试集，对其进行核主成分-k近邻分类。

首先，将训练集T标准化以消除量纲带来的影响，然后进行核变换。由于高斯径向基的参数难以选定，对核参数分别选取了240，600，1 000参数，分别采用Fisher判别，k近邻，Logistic回归3种分类方法进行试运算，将得到的9个心脏疾病分类正确率进行比较。可以看出在同一种分类方法中，心脏疾病分类的正确率对于核参数的选择是鲁棒的[20]。随机选取18个2σ2的不同取值，分别为240，300，360，400，420，480，500，540，600，660，700，720，780，800，840，900，960，1 000。核变换后进行主成分分析，分别使用了Fisher判别，k近邻分类，Logistic回归(临界概率值选为0.5)对不同参数下的主成分分析的结果进行心脏疾病分类，得到了在18个不同参数下的3种分类方法的正确率。通过表2可以看出k近邻分类方法的正确率高于其余两种。

表2 在不同参数下的3种分类方法的正确率

得到表2后对其数值进行排秩，得到表3，从表3中看到有相同秩，因此，Friedman秩方差检验中选用c统计量。由表3可以计算得到c27.587。接受H0，即认为各个参数之间的正确率无差异。在k近邻心脏疾病分类结果中选取正确率最高的且主成分个数最少的参数，即2σ2=720，其中训练集的主成分个数为5。

表3 在不同参数下的3种分类方法的心脏疾病分类正确率秩排序

选定参数及分类方法后，将其用于心脏疾病分类测试集M。通过高斯径向基核函数将M进行变换，并且通过R中MVN包对变换后的心脏疾病测试集M′进行了多元正态性检验，如果测试集服从多元正态分布，则这些点应与直线有着较好的拟合。由图1可以看出，这些点与直线的拟合并不是很好，由此可以说明变换后的测试集并不服从多元正态分布。

图1 心脏疾病测试集M′的多元正态性检验

接下来对变换后的心脏疾病测试集进行主成分分析，主成分的个数为5。之后进行k近邻分类，其正确率可以达到92%。如果直接使用主成分分析-k近邻，其主成分个数在心脏疾病训练集有25个，心脏疾病测试集达到28个，这使得计算代价大大提高。心脏疾病测试集上使用KPCA与PCA的结果(取前5个主成分)比较见表4。由表4可以看出，KPCA方法不仅仅主成分个数更少，仅需要5个主成分即可达到97%的贡献率，且第一主成分的方差极大，表明KPCA中第一主成分所含信息量极多。而PCA前5个主成分仅仅达到了65%的贡献率，并且一共需要28个主成分才能够符合本研究97%的选择条件，第一主成分所含的信息量也只能与KPCA的第二主成分相当。由此可以看出，KPCA的计算代价与PCA的计算代价相比很小。

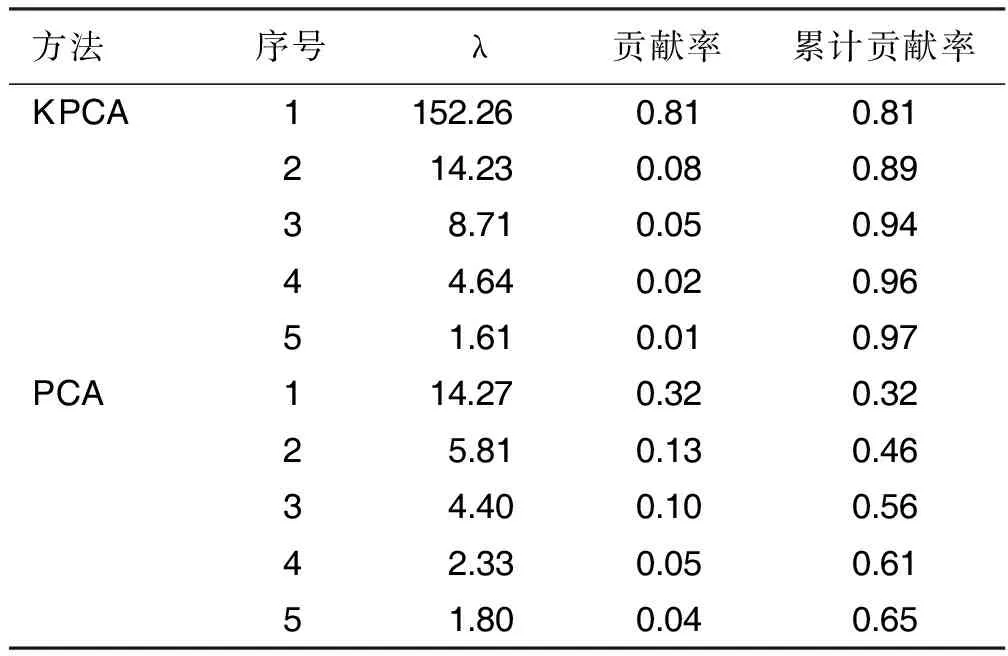
表4 KPCA与PCA结果比较

在心脏疾病训练集上PCA的降维效果也不理想。心脏疾病训练集中PCA需要25个主成分，而KPCA仅需要5个。心脏疾病训练集上PCA的分类正确率仅有81.25%，而KPCA可以达到88.75%。详见表5。

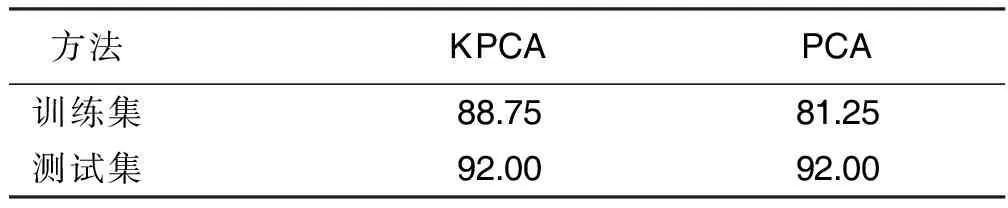
表5 心脏疾病数据集上KPCA与PCA的分类正确率 单位：%

不管是在主成分个数还是所含信息量，相对于PCA来讲，KPCA的优势非常明显，其降维效果有显著提升，极大地减小了心脏疾病数据集中非线性因素的影响，从而使后面的数据处理更加简单快捷。

5 讨 论

本研究基于KPCA-KNN方法对心脏疾病分类。

方法上，通过Friedman秩方差检验法对高斯径向基核函数的参数进行了选取，使用了核主成分分析-k近邻方法对心脏疾病数据集进行分类；理论上，通过Q-Q图检验了核变换后的心脏疾病数据的多元正态性与高斯径向基核函数参数的鲁棒性；最后将KPCA-KNN方法应用于心脏疾病SPECIF数据集上，与PCA-KNN方法相比，可以看出KPCA-KNN方法对心脏疾病数据集分类降维效果较好，在心脏疾病测试集上其分类准确率可达92%，并且分类准确率比原始的CLIP3算法提高了15%。总体看来，在处理心脏疾病数据这一类非线性分类问题时，KPCA-KNN方法使得解决问题又多了一条有效的途径。