基于两阶段Gamma过程的机械产品剩余寿命预测研究*

姜 洋

(浙江机电职业技术学院 现代信息技术学院，浙江 杭州 310053)

0 引 言

传统机械产品的可靠性评估大多基于大样本假设下的强度-应力干涉理论。随着科技的进步，以高可靠性、长寿命、小子样为特征的机械装备的可靠性评估难以满足强度-应力干涉模型的大样本要求，因此，需要充分利用机械装备全寿命周期内的退化信息，同时考虑机械装备运行过程中的环境条件、材料本身的随机性等因素，通过分析机械产品的性能退化数据建立产品的可靠性分析模型。

产品因温度、湿度和磨损等原因会发生连续退化。从20世纪70年代开始，许多学者对具有退化特性的产品可靠性评估进行了研究。文献[1]用线性退化模型描述了厚膜电阻的退化过程，完成了厚膜电阻在温度应力下的可靠性评估。文献[2]利用加速退化数据得到了长寿命产品的可靠性评估新方法。文献[3]利用B-S分布近似产品的可靠度，建立了多元退化下的可靠性模型。文献[4]详细描述了Gamma过程作为静态应力-强度模型的统计特性、参数估计以及在产品寿命预测研究中的应用。文献[5]提出了基于随机参数Gamma过程模型的剩余寿命预测方法，结合产品加速老化数据，提高了预测结果的可信度。

机械产品的运行过得中，除了受到激发连续退化的平稳载荷外，还受到外部环境和载荷波动的冲击载荷，因此，在机械产品寿命预测中，计及冲击失效的竞争效应是提高机械产品寿命预测精度的重要因素。文献[6]587根据性能退化数据建立了对产品连续退化过程的分析模型，并通过泊松过程描述了随机冲击对产品的离散作用过程，最终得到了产品实际可靠性模型。文献[7]根据系统在变点前后受到的外部冲击的损坏量所服从的分布不同，运用不确定性理论和机会理论，得到了3种不同冲击模式下的确信可靠度模型。

传统的可靠性分析模型是建立在二态(正常、故障)假设基础上的，而越来越多的工程实践表明，机械产品在全寿命周期内具有一段潜在故障区间，即产品从正常状态到故障状态的过渡状态，在潜在故障状态下，产品相对正常状态具有较高的失效率和性能退化率。机械产品疲劳裂纹的生长过程是最典型的实例。因此，应用传统的两态可靠性评估模型进行机械产品寿命预测在潜在故障阶段将产生较大的估计误差，如何将机械产品的二态生命周期拓展为三态寿命周期，进行可靠性评估和寿命预测是另一个亟待解决的问题。

本文综合考虑机械产品的连续退化过程和离散退化过程，并基于延迟时间理论描述产品的加速退化过程，得到退化型机械产品在冲击载荷下的可靠性评估方法，并通过仿真实例验证该方法的正确性与有效性。

1 可靠性模型

由CHRISTER教授在1973年提出的三态可靠性评估模型[8]中，提出了延迟时间的概念。延迟时间理论认为，产品的全寿命周期可以分为两个阶段：第一阶段为正常阶段，包括产品投入使用到缺陷发生时刻t0；第二阶段为延迟时间阶段，包括缺陷发生时刻t0到产品发生故障，这两个阶段是互相独立的[9]。

性能退化水平如图1所示。

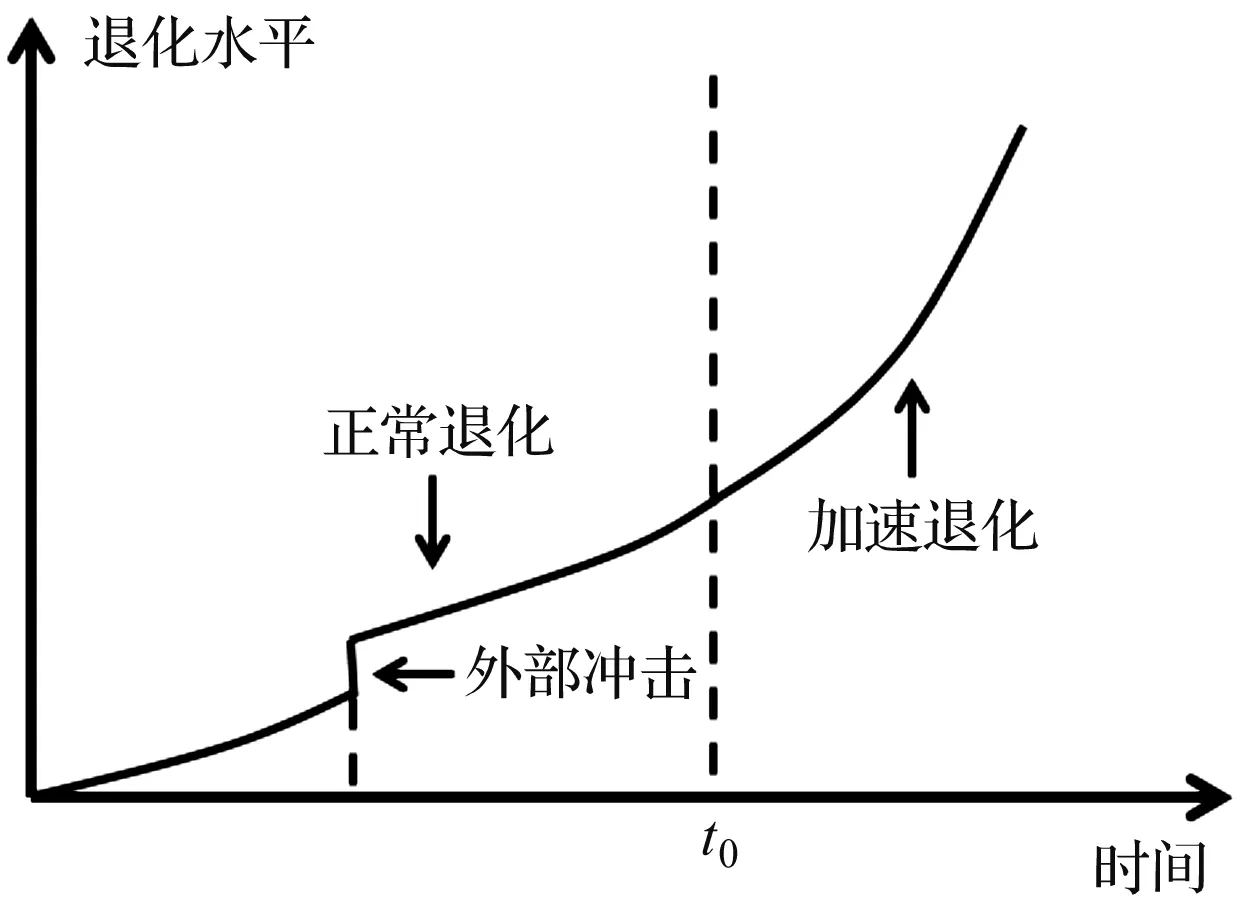
图1 两阶段延迟时间理论

根据时间延迟理论，笔者将机械产品的全寿命周期从传统的两态空间拓展为三态空间，即在正常状态和故障状态之间，增加一个潜在故障区间(加速退化阶段)，机械产品在该区间运行时虽然能够工作，但是退化率相较于正常状态显著提升。

用t0表示两个阶段的分界时间点，可以根据产品生命周期所处时间t与t0的关系将系统状态s分为3个状态：

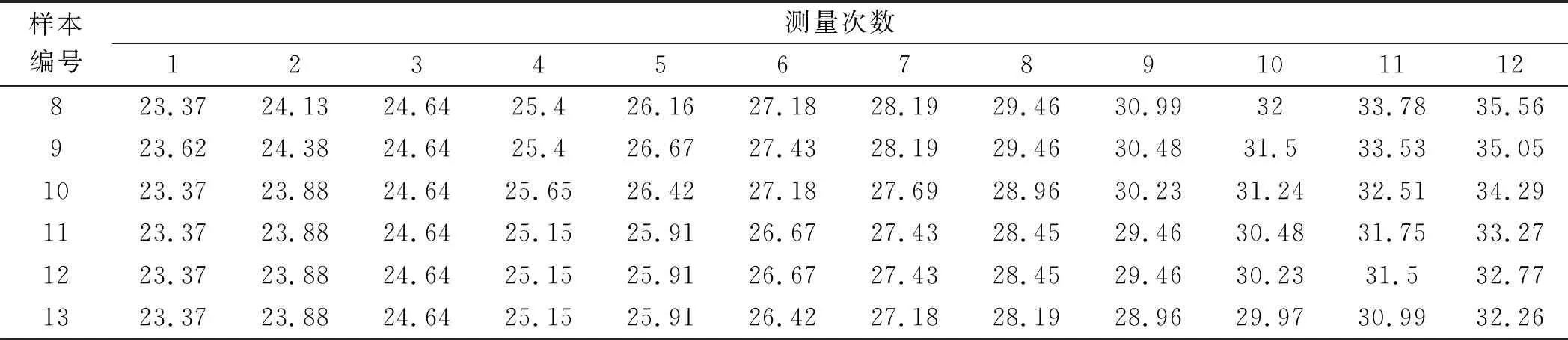
(1)正常退化态s0。t

(2)加速退化态s1。t>t0，产品加速退化但没有发生故障；

(3)故障态s2。系统发生故障。

威布尔分布作为一种连续的概率分布模型[10]，是描述机械产品可靠性分布的最常用分布。因此，假设t0服从威布尔分布，且用β0表示比例参数，β1表示形状参数。t0的累积分布函数和概率密度函数分别用F(t0)和f(t0)表示。

伽马过程具有独立、非负增量的特性，可以很好地描述机械产品因磨损等原因造成的严格单调的退化过程[11]。

假设产品的连续退化过程服从伽马过程，则任意时刻t产品的连续退化量x(t)服从伽马分布，即：

(1)

式中：kt—形状参数；λ—尺度参数。

根据上述假设，产品首先处于正常退化态，并且性能从0开始退化。假设正常退化态下的退化过程服从参数为(k0,λ0)的伽马过程，则产品性能退化量的均值和方差分别为：

E=μ0tt

(2)

(3)

当产品处于加速退化状态下，产品性能从t0时刻的x(t0)开始退化。假设加速退化态下的退化过程服从参数为(k1,λ1)的伽马过程，因此有：

E=μ0t0+μ1(t-t0)t>t0

(4)

(5)

文献[12，13]讨论了产品退化过程的参数拟合问题，并指出产品退化量的方差随时间线性变化是合理的，即σ=σ0=σ1。

因此，产品全生命周期下产品退化量的期望和方差可以表示为：

(6)

Var=σ2t

(7)

在产品的使用中，除了有随时间推移而产生的连续退化外，还有来自外界的随机冲击造成的离散退化。冲击载荷作用后，产品的退化水平会发生明显阶跃性增长，因此，机械产品的退化失效是连续退化失效和随机冲击引起的离散退化失效竞争的复合过程。

单次冲击载荷的发生时间和退化效应幅值是一个随机变量，一般情况下采用复合泊松过程描述上述随机性。

假设时刻t已发生的冲击次数N(t)服从泊松过程，则t时刻发生n(n=0,1,2,…)次冲击的概率为：

(8)

式中：α—泊松过程的强度参数。

假设各次冲击造成的退化量独立同分布，则退化量为：

Di～N(e,v2)

(9)

式中：Di—第i(i=0,1,2,…)次冲击造成的退化量；e—一次冲击造成退化量的均值；v2—一次冲击造成退化量的方差。

设y(t)是t时刻由冲击造成的退化量，则有：

(10)

由于各次冲击造成的退化量独立同分布，y(t)仍然服从正态分布，且有：

y(t)～N(N(t)e,N(t)v2)

(11)

综合考虑连续退化和随机冲击的影响，根据累计损伤模型，t时刻产品的退化量u(t)应该由x(t)和y(t)共同组成，因此有：

u(t)=x(t)+y(t)

(12)

假设产品的退化量失效阈值为L，则t时刻系统可靠度可以表示为：

(13)

根据文献[14]，利用B-S分布近似可得：

(14)

式中：Φ(·)—标准正态分布的累积分布函数；Eu—t时刻产品退化水平的期望。

Eu表达式为：

(15)

考虑t0的随机性，可以得到产品全生命周期的可靠性模型为：

(16)

2 仿真分析

金属材料是各种机械产品的主要材料，金属材料的裂纹扩展是金属材料可靠性的重要问题之一。

某金属材料的性能退化数据[6]590如表1所示。

表1 某金属性能退化数据

续表

该数据集共有13个样本，每10 000次循环进行一次测试，每个样本测试11次。

本文基于表1的退化数据，采用最大似然估计方法[15]对模型参数进行拟合。

考虑延迟时间后的加速退化过程，参数拟合的结果如表2所示。

表2 考虑延迟时间加速退化参数拟合结果

不考虑延迟时间后的加速退化过程，参数拟合结果如表3所示。

表3 不考虑延迟时间加速退化参数拟合结果

根据上述参数拟合结果，同时假设泊松过程的强度参数α=0.1，一次冲击造成退化量的方差v2=0.044 1，退化量失效阈值L=50，可得出该金属材料的可靠性模型；并基于MATLAB进行不同平均冲击强度e下的仿真。

可靠度变化趋势如图2所示。

图2 可靠性评估结果

图2表明：在考虑冲击载荷时，金属材料可靠运行寿命显著减小，工作寿命减小的程度和冲击载荷的强度分布正相关。

由于机械产品在实际运行工况下，冲击载荷无可避免，采用本文提出的退化失效与冲击失效竞争情况下的损伤累积模型，能够更加准确地预测机械产品的剩余寿命。

在不考虑加速退化的状态采用单阶段Gamma模型，考虑加速退化的状态采用两阶段Gamma模型，笔者根据金属材料性能退化数据进行了剩余寿命预测仿真。

仿真结果如表4所示。

表4 寿命评估结果

由表4可知：在不考虑加速退化状态时，采用单阶段Gamma过程模型的寿命预测结果约30万次循环；而考虑加速退化状态时，采用两阶段Gamma过程的寿命评估结果约20万次循环。

同时，笔者根据表1的退化试验数据，采用最大似然估计法对Gamma模型参数进行拟合，预测该金属材料的实际寿命长度。据拟合结果显示;该样本1寿命最短，为12.4万次循环;样本13寿命最长,为25.9万次循环。

对比表4可以得出，考虑金属材料在全寿命周期范围内的潜在故障区间更符合实际金属材料性能退化轨迹，其预测结果也更为精确。

3 结束语

在进行机械产品寿命预测时，由于传统的两状态可靠性评估存在较大的估计误差，在计及冲击载荷条件下，笔者提出了一种基于两阶段Gamma过程模型的三态机械产品的寿命预测方法；该方法基于时间延迟模型，描述了产品的加速退化过程，并基于该方法对金属材料的裂纹扩展过程进行了分析。

研究结果表明：

(1)相对于传统两状态的可靠性评估模型，基于两阶段Gamma过程模型的三态寿命预测方法对机械产品的可靠性评估结果具有更高的精度；

(2)在考虑冲击载荷条件下，考虑全寿命周期内的加速退化阶段更符合机械产品性能退化轨迹，且能有效提升剩余寿命预测的准确性。

大多机械产品的运行工况比较复杂，仅靠单一性能指标难以全面、准确反映产品的退化过程。因此，在今后的研究中，笔者将综合考虑多个关键性能指标，来进行产品的可靠性建模和评估。