基于ADAMS的6PSS并联机构多目标优化研究*

郑江涛,田大鹏*,高志良

(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033; 2.中国科学院大学,北京 100049)

0 引 言

并联机构具有结构紧凑、刚度高、动态响应快等优点,在先进制造装备、生物医学装置、航空航天运动模拟等领域的应用已取得了巨大的成功[1-3]。然而,并联机构的性能与它的结构参数密切相关,当其结构参数选择不太合适时,并联机构的运动性能可能会很差。

因此,许多研究者一直致力于并联机构性能的优化研究。最常用的优化方法大致可以分为两类:(1)基于目标函数的优化方法;(2)基于性能图谱的优化方法。

目标函数法的原理是:首先,根据优化指标建立目标函数和约束条件;然后,使用算法搜索优化结果。文献[4]采用了穷尽搜索最小化算法,将并联机构可操作性和工作空间大小的度量结合起来,并通过运动学优化过程得出了可操作性和空间利用率之间的最佳折衷设计。文献[5]在考虑了关节限制和连杆干涉的约束条件下,采用随机搜索算法对Delta机器人和Gough-Stewart平台进行了优化,找到了使有效规则工作空间最大化的机械手几何结构。文献[6]以运动学雅克比矩阵的条件数和可操作度作为目标函数,采用了多目标进化算法NSGA-II对六自由度运动模拟平台进行了优化。文献[7]以雅可比矩阵的性能指标条件数、刚度、速度极值作为目标函数,采用了罚函数法处理约束条件,提出了性能分类的方式作为多目标优化的准则,最后利用遗传算法进行了参数优化。

该方法多用于参数变量较多,且目标函数过于复杂的情况。

基于性能图谱的优化设计方法的关键是:在一个有限的区域内表达出机构的性能与尺寸的关系,进而得到机构的性能图谱。文献[8]利用这种方法对3PRS机构和二自由度球面5R并联机构进行了优化,使其在工作空间内有较好的运动和力传递性能。文献[9]建立了3-RUU微动并联机构的尺寸型模型,并根据尺寸型模型及定义的性能指标绘制了反映机构性能与尺寸参数关系的性能图谱。文献[10]采用了综合性能图谱法结合主成分分析法,对5-PSS/UPU并联机构进行了多目标优化。

该方法可以在一个有限的设计空间内直观地表达出设计指标和相关设计参数的关系,但存在的最大问题是:当需要优化的特征参数较多时,不能在一个有限的空间中完整地表示出其性能图谱。

以上两种优化方式,都存在比较繁琐、复杂的特点。为找到一种更容易、更快速的优化方法,研究人员利用ADAMS、Isight等软件集成的先进优化算法。该方法实际上也是一种基于目标函数的优化方法,但其操作方便,更为便捷和直观。如文献[11]基于ADAMS对空间光学遥感器6自由度定位器的结构进行了单目标的优化设计。文献[12]采用了虚拟样机技术,对6SPS并联机构的驱动力进行了单目标的优化。

本文采用基于ADAMS的多目标优化设计方法,研究设计变量的变化对目标函数的影响,而且利用ADAMS集成的优化算法,对6PSS并联机构的承载能力和运动范围进行优化,为6PSS并联机构的结构设计和进一步的研究奠定基础。

1 参数化模型的建立

1.1 设计变量创建

6PSS并联机构的构型如图1所示。

图1 6PSS并联机构示意图

由图1可知:就此机构而言,需要进行优化设计的结构参数有:动平台球铰几何中心分布的半径r、定平台球铰几何中心分布的半径R、动平台球铰长边对应的圆心角α、定平台球铰短边对应的圆心角β、初始高度H(动平台球铰中心点所在的平面和定平台球铰中心点所在的平面之间的距离)。

因此,6PSS并联机构的设计变量写成矢量的形式为:

x=(x1,x2,x3,x4,x5)T=(r,R,α,β,H)T

其中,各设计变量之间相互独立,各分量的物理意义如表1所示。

表1 设计变量的物理意义及单位

根据6PSS并联机构的实际操作空间、机械结构的约束要求,以及避免发生奇异性的要求,定平台和动平台所对应的球铰分布不能相似,所以各个设计变量的取值范围为:

1.2 参数化模型创建

本文采用参数化关键点坐标的方法,建立6PSS并联机构的参数化模型[13]。参数化点的坐标如表2所示。

表2 参数化点的坐标

创建完参数化点后,需要再根据图1创建相应的构件,然后添加相应的运动副。

为了不失一般性,笔者首先在动平台质心处加一点驱动,六自由度方向同时加载正弦位移/转角驱动函数,沿x、y、z方向的位移函数设置为2sin(2πt),绕x、y、z轴旋转的驱动函数为2dsin(2πt);利用ADAMS模型的运动学逆解仿真结果得到移动副1～6对应的样条函数,即SPLINE_1-SPLINE_6;然后去除ADAMS模型的动平台质心的点驱动,在每个移动副关节处加上平移驱动MOTION_1-MOTION_6,设定驱动函数为AKISPL(time,0,SPLINE_1,0),…,AKISPL(time,0,SPLINE_6,0);最后在动平台的质心处添加外部载荷,力的大小F=10 N,方向竖直向下,力矩大小T=10 N·m,方向竖直向下。

完成以上工作后,所创建的6PSS并联机构的参数化模型如图2所示。

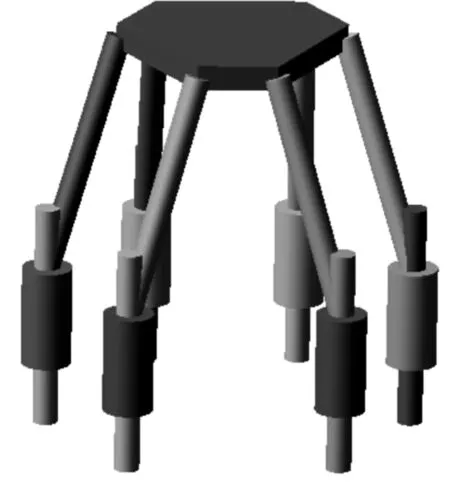
图2 6PSS并联机构的参数模型

1.3 目标函数创建

对于6PSS并联机构而言,其要有较高的承载能力和较大的运动范围,将其转化为数学模型,即是在动平台承受相同的负载,且6个驱动副的运动规律相同时,6个驱动副受力的最大值最小,动平台质心的动坐标系相对于定坐标系x、y、z轴的3个转动角的最小投影角最大。

在ADAMS中创建两个测量函数:

Mea_1=max(max(max(Force_1,Force_2),
max(Force_3,Force_4)),max(Force_5,Force_6))

(3)

Mea_2=min(min(ABS(Alpha),ABS(Beta)),
ABS(Gamma))

(4)

式中:Mea_1—每一个运动周期内6个移动副驱动力的最大值;Mea_2—每一个运动周期内动平台的质心绕定坐标系x、y、z轴的3个转动角的最小值;Force_i(i=1、2……6)—6个移动副驱动力的测量函数;Alpha,Beta,Gamm—动坐标系相对于定坐标系的x、y、z轴的3个转动角的测量函数。

在一个周期内,6个移动副的驱动力和动平台质心的转角随时间成正的正弦规律运动,因此,分别取一个周期内的均值作为目标函数。因为要求并联机构有较高的承载能力和较大的运动范围,即并联机构驱动力最小和转动角最大,此处选择目标函数分别为:min(f1(x))和max(f2(x));其中,f1(x)、f2(x)可以表示为:

f1(x)=Averageof(Mea_1)=Averageof(max(max(max(Force_1,Force_2),

(5)

max(Force_3,Force_4)),max(Force_5,Force_6)))

f2(x)=Averageof(Mea_2)=Averageof(min(min(ABS(Alpha),ABS(Beta)),ABS(Gamma)))

(6)

1.4 约束函数创建

1.4.1 球面副转角的限制

6PSS并联机构共有12个球面副,球面副的转角范围是有限制的。

球面副的转角约束条件可以表示为:

(7)

式中:θi—第i个球面副的基座固结的坐标系的z轴和球面副连接的杆向量li之间的夹角;ni—第i个球面副的基座的z向向量;R—球面副相对于固定坐标系的姿态。

因此,笔者分别建立12个球面副转角的测量函数,并命名为MEA_ANGLE_i,(i=1,2…12);然后,建立球面副的约束函数MEA_ANGLE_i-30°≤0,(i=1,2…12)。

1.4.2 连杆的干涉

连接上下平台的连杆是有一定的尺寸大小的;因此,各杆之间可能发生干涉。这里假设各杆都是圆柱状的,其直径为D,若Di(i=1,2…6)为两相邻中心线之间的最短距离,则两杆不发生干涉的条件是Di≥D[14]。对于连杆之间的干涉约束,通过在连杆之间添加实体接触命令,使各个连杆之间不能相互穿透几何体,从而可以防止发生干涉。

所以,由参数化模型时各个设计变量的约束和球面副转角的约束,共同组成了6PSS并联机构的约束条件,即为:

(8)

2 设计变量对目标函数的影响

2.1 动平台球铰几何中心圆的半径对目标函数的影响

笔者在ADAMS中,研究动平台球铰几何中心圆的半径对目标函数的影响。目标函数随动平台球铰几何中心圆的半径变化曲线,如图3所示。

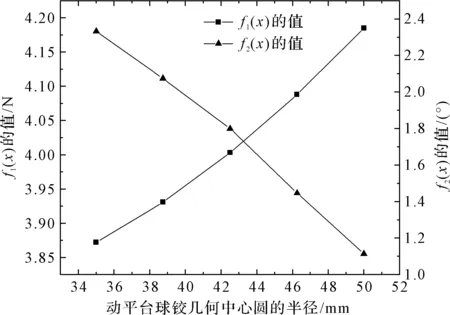
图3 目标函数随动平台球铰几何中心圆的半径变化曲线

从图3可以看出:目标函数f1(x)的值与动平台球铰几何中心圆的半径成正相关的关系,目标函数f2(x)的值与动平台球铰几何中心圆的半径成负相关的关系。

2.2 定平台球铰几何中心圆的半径对目标函数的影响

笔者在ADAMS中,研究定平台球铰几何中心圆的半径对目标函数的影响。目标函数随定平台球铰几何中心圆的半径变化曲线,如图4所示。

图4 目标函数随定平台球铰几何中心圆的半径变化曲线

从图4可以看出:目标函数f1(x)的值与定平台球铰几何中心圆的半径,在一定范围内成负相关的关系;目标函数f2(x)的值与动平台球铰几何中心圆的半径,一定范围内成正相关的关系。

2.3 动平台球铰长边对应的圆心角对目标函数的影响

在ADAMS中研究动平台球铰长边对应的圆心角对目标函数的影响。目标函数随动平台球铰长边对应的圆心角变化曲线,如图5所示。

图5 目标函数随动平台球铰长边对应的圆心角变化曲线

从图5可以看出:目标函数f1(x)的值与动平台球铰长边对应的圆心角成负相关的关系,目标函数f2(x)的值与动平台球铰长边对应的圆心角成负相关的关系。

2.4 定平台球铰短边对应的圆心角对目标函数的影响

在ADAMS中研究定平台球铰短边对应的圆心角对目标函数的影响。目标函数随定平台球铰短边对应的圆心角变化曲线如图6所示。

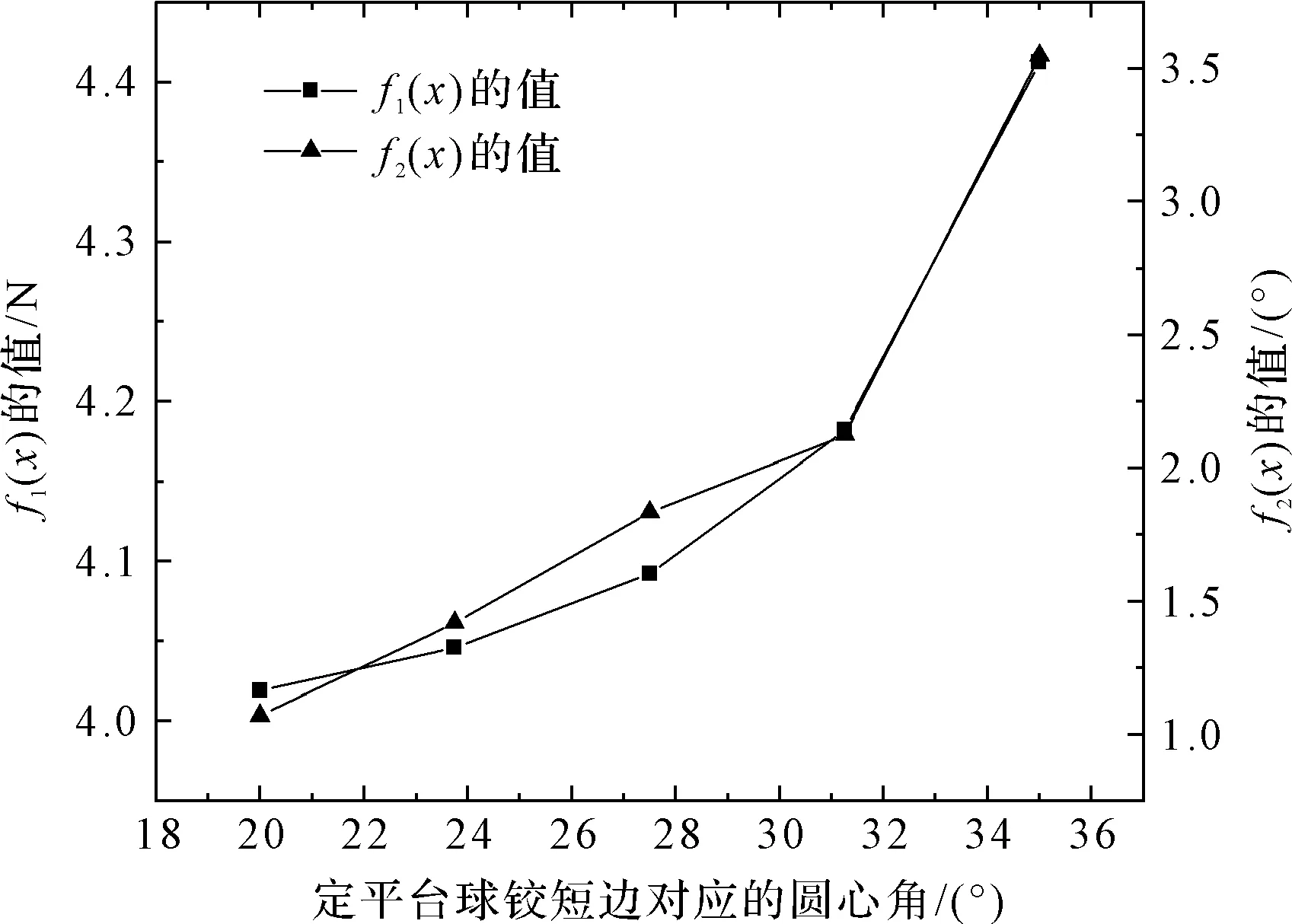
图6 目标函数随定平台球铰短边对应的圆心角变化曲线

从图6可以看出:目标函数f1(x)的值与定平台球铰短边对应的圆心角成正相关的关系,目标函数f2(x)的值与定平台球铰短边对应的圆心角成正相关的关系。

2.5 初始高度对目标函数的影响

在ADAMS中研究初始高度对目标函数的影响。目标函数随初始高度变化曲线如图7所示。

图7 目标函数随初始高度变化曲线

从图7可以看出:目标函数f1(x)的值与初始高度成正相关的关系,目标函数f2(x)的值与初始高度成正相关的关系。

3 并联机构的优化

本文第2节研究了设计变量的变化对目标函数f1(x)和目标函数f2(x)的影响,发现同一个设计变量的变化,往往会使不同的目标函数产生不同的(甚至是截然相反的)变化趋势。因此，为了使并联机构的性能最优,需要对其进行多目标优化设计。

3.1 基于线性加权和法的多目标优化

本文采用线性加权和法将多目标优化问题重新构造成一个新的评价函数,从而将多目标优化问题转变为求评价函数的单目标优化问题[15],即:

(9)

在ADAMS中进行单目标的优化可得:

因为目标函数f1(x)优化的目标是尽可能地小,目标函数f2(x)优化的目标是尽可能地大,它们的优化方向相反,故对f2(x)取负值进行计算;取λ1=0.8，λ2=0.2。

综上所述,其评价函数为:

(10)

在ADAMS中进行多目标的优化,其优化过程的设置如图8所示。

图8 并联机构的多目标优化

图8中,min(FUNCTION_MEA_19)=minF(x),DV_J1=α,DV_J2=β,DV_L=H,DV_Ra=r,DV_RB=R,OPT_CONSTRAINT_1=MEA_ANGLE_i-30°≤0。

然后,利用ADAMS集成的优化算法进行优化,优化后的结构变量如表3所示。

表3 并联机构优化前后的参数值

在ADAMS中,笔者对6PSS并联机构优化前后的移动副驱动力的最大值和动平台的质心转角最小值进行测量。

移动副驱动力最大值变化曲线结果如图9所示。

图9 优化前后移动副驱动力最大值变化曲线

动平台质心转角最小值变化曲线如图10所示。

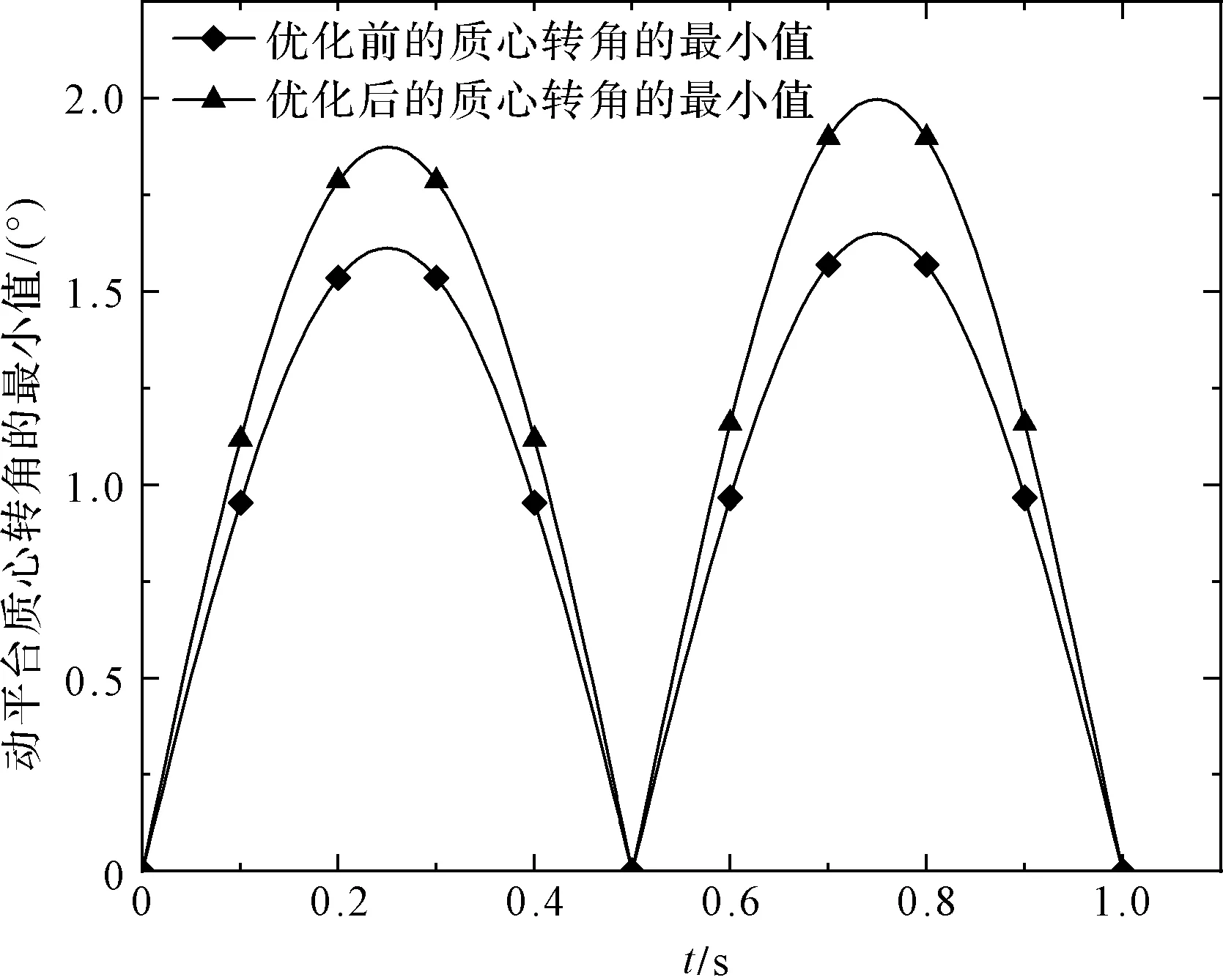
图10 优化前后动平台质心转角最小值变化曲线

由图(9,10)可知:优化后,移动副驱动力最大值的均值比初始值减小了6.5%,动平台质心转角最小值的均值比初始值增大了17.9%。

同时,笔者在并联机构的运动空间内选取了7组典型的静态的不同的位姿,测量6个移动副在优化前后最大的驱动力,如图11所示。

图11 静平衡下不同位姿6个移动副最大驱动力优化前后变化曲线

由图11可知:优化后在静态位姿下,移动副的最大驱动力减小了,从而提高了电机的重力补偿能力。

3.2 基于蒙特卡罗法的工作空间分析

蒙特卡罗法是一种通过随机抽样来解决数学问题的数值方法,该方法特别适用于计算由复杂曲面包围的体积[16，17]。例如机械手工作空间的体积,因为它在计算工作空间体积时不需要边界曲面的分析表达式;相反,只需要确定机械手末端的参考点是否可以到达空间中随机选择的点。6PSS并联机构的工作空间是一个不规则的三维曲面所包围的区域,因此,本文采用蒙特卡罗法对6PSS并联机构的工作空间进行求解。

该方法是基于并联机构的运动学位置逆解而进行的一种搜索方法。其原理如下:首先给出一个包含并联机构工作空间的范围,在此范围内,产生大量随机的点;然后由机构的运动学逆解判断每一点是否满足约束条件,如果满足约束条件则是空间内的点,如果不满足,则剔除[18，19]。所有满足约束条件的点组成了机构的工作空间。

由蒙特卡罗法得出的值并不是一个精确值,而是一个近似值,但是当投点的数量越来越大时,这个近似值也越接近真实值。文献[20]中首次基于蒙特卡罗法给出了计算机械手工作空间的公式,即公式(11);并给出了几个实际的例子,从而证明了蒙特卡罗法是一种简单、易于实现、自然适用于计算机应用的方法,即:

式中:V1—机构的工作空间体积;V2—总的给定空间体积;n—机构满足约束条件的位置点数;N—总的点数。

根据蒙特卡罗法求解工作空间的原理,笔者在MATLAB中进行编程和仿真,求得优化前后的n/N的数值,如表4所示(N=1000 000)。

表4 优化前后n/N的数值对比

优化前的工作空间为:40×40×20×0.081=2 592 mm3,优化后的工作空间为40×40×20×0.089=2 848 mm3;可见,其工作空间提高了9.8%。

优化前的工作空间如图12所示。

图12 优化前机构的工作空间

优化后的工作空间如图13所示。

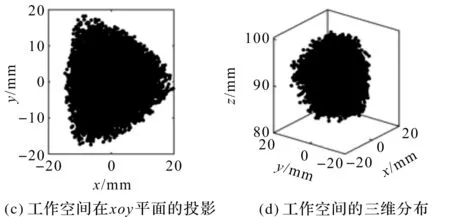
图13 优化后机构的工作空间

4 结束语

本文基于ADAMS软件对6PSS并联机构进行了多目标的优化设计;首先建立了机构的参数化模型、约束条件和目标函数,然后研究了设计变量的变化对单目标函数的影响,最后采用线性加权和法,进行了多目标优化,优化后移动副驱动力最大值的均值比初始值减小了6.5%;利用蒙特卡罗法计算了机构的工作空间,优化后工作空间提高了9.8%,提高了机构的承载能力,扩大了机构的运动范围。

与其他多目标优化方法相比,这种方法更为简单、直观,可以高效率地用于多参数的复杂并联机构的优化设计。