基础平动激励下的电磁轴承-柔性转子系统振动控制研究*

陈润田,祝长生

(浙江大学 电气工程学院,浙江 杭州 310027)

0 引 言

电磁轴承通过可控电磁力支承转子,具有无机械摩擦、无需润滑、复杂环境适应性强等优点。另外,通过控制电磁力,它还可以主动调节支承的动力学特性,在保证转子稳定悬浮的同时,可以抑制转子系统的振动[1]。

目前,对电磁轴承-转子系统动力学及控制的研究,主要是在假设基础处于不动或忽略基础激励的条件下进行的。但是,对于许多电磁轴承-转子系统,就必须考虑基础激励的影响,否则电磁轴承-转子系统不仅不能稳定工作,甚至会出现转子与保护轴承碰撞或系统失稳的现象[2-4]。因此,在存在基础激励的情况下,需要考虑转子系统的动态响应,应保持转子和定子之间的相对位移小于安全气隙,以免转子碰撞保护轴承或系统失稳。

按照激励的特性,基础激励可以分为单频激励、多频激励、随机激励(包括地震激励)及其组合等形式。基础可以为刚体,也可以为柔性体;柔性基础的特性相对刚性基础的特性更加复杂。对于刚性基础,基础的运动状态可以用3个位移和3个角度变量来表示。按照基础的运动状态,基础激励又可以分为平动激励、锥动激励[5]以及混合运动激励[6]。其中,平动激励是基础在某个方向上发生平动运动,也就是基础的某个位移变量发生变化,而角度变量保持不变;锥动激励为基础以其某一点为中心做角向运动,某个角度变量发生变化,而这个中心点的位置变量保持不变;混合运动激励基础的位置和姿态都发生变化,是最一般的基础激励形式。目前,对基础激励的研究主要以平动激励为主。

KEOGH P S等[7]针对基础冲击激励下,给电磁轴承-转子系统带来的不良影响,对谐波控制器进行了优化设计,所设计的控制器可在有限时间内抑制系统的瞬态响应。MURAL Y等[8]收集了地震波波形,并将其施加于电磁轴承-柔性转子系统,对其振动响应进行了测试,但并未提出有效的控制方法。SUZUKI Y[9]根据电磁轴承-柔性转子系统在基础激励条件下的振动响应特性,设计了一种基于FIR(finite impulse response)和IIR(infinite impulse response)的加速度前馈补偿滤波器,用于抑制单个周期的正弦冲击激励和周期性正弦激励给系统带来的不良影响。COLE M O T等[10]将基础激励以位移的形式引入到电磁轴承-柔性转子系统中,提出了一种基于状态反馈的自适应Q控制方案,但这种控制方法对模型精确性要求较高。KASARDA M E等[11]搭建了一个小型的非旋转试验装置,并对此进行了测试,以研究正弦基础运动对电磁轴承支撑目标转子质量的影响;但是其缺陷是并未考虑转子的旋转。KANG M S等[12]研究了不依赖被控模型的自适应Fx-LMS的加速度前馈补偿控制器,实现了对单自由度电磁悬浮系统的振动控制。MARUYAMA Y等[13]利用干扰观测器估算的干扰信号来补偿定子运动对转子带来的影响,其补偿的效果取决于观测器的估算精度。MARX S等[14]考虑了带有两个电磁轴承的四自由度刚性转子模型,将PD反馈和最优前馈控制程序进行组合,有效地抑制了谐波基础运动对磁悬浮转子系统的有害影响。KAMEL M等[15]研究了在多参数激励下,具有二次非线性和三次非线性的周期性时变刚度的电磁轴承-转子系统的共振情况,并应用多时标技术,求解了其控制系统的非线性微分方程。

在国内,黄春新[16]通过仿真,分析了电磁轴承-转子系统悬挂在机翼下和在地面上旋转工作时的不平衡响应和激励响应。祝长生等[17]通过实验,研究了电磁轴承-转子系统中基础的横向振动对电磁轴承转子系统动力特性的影响,研究结果表明,传统的PID控制器对电磁轴承基础横向振动的抑制能力非常有限。HAN Qin-kai等[18]利用Lagrange方程和有限元法,建立了具有六自由度基础运动和质量不平衡的偏置单盘柔性转子系统运动微分方程的一般表达式,发现时变基础运动不仅在转子系统上产生附加的参数时变阻尼和刚度效应,还会产生附加外激励力。

针对基础平动激励条件下电磁轴承-柔性转子系统的振动控制,笔者通过建立电磁轴承-柔性转子系统运动方程及状态空间方程,提出一种基于LMS算法的,以基础加速度为输入信号的自适应控制器,验证基于LMS算法的变步长自适应控制策略对基础平动激励引起的系统振动响应的有效性。

1 基础平动激励下电磁轴承-柔性转子的动力学模型状态方程

常见的电磁轴承-柔性转子-基础系统基本结构如图1所示。

图1 柔性转子基础系统示意图O(x0y0z0)—固定在地面的绝对坐标系;Ob(xbybzb)—固定在基础上的相对于地面的坐标系;Or(xyz)—固定在转子上的相对于基础的坐标系

本文主要研究电磁轴承-柔性转子系统的径向振动特性,而忽略轴向振动及扭转振动的影响。

1.1 基础静止条件下柔性转子系统的动力学方程

当柔性转子系统的基础处于静止状态时,基础和地面相对静止,即有:

x=x0

(1)

式中:x—转子相对于基础的位移矢量,m;x0—转子相对于地面的位移矢量,m。

对具有n个节点的柔性转子系统,笔者利用有限元或集中参数法进行建模,容易得到柔性转子系统的动力学方程为:

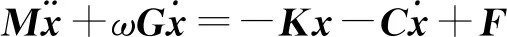
(2)

式中:M—转子4n×4n维的质量矩阵,kg;G—转子4n×4n维的陀螺效应矩阵;K—转子4n×4n维的等效刚度矩阵,N/m;C—转子4n×4n维的等效阻尼矩阵,N/m·s-1;F—转子受到的除基础激励外的激励力矢量,N;ω—转子的转速,r/min。

1.2 基础平动激励条件下转子系统的动力学方程

在转子系统的基础出现运动后,柔性转子系统的运动方程仍然与式(2)类似,但系统中与刚度和阻尼相关的力,将和转子与基础之间的相对位移和相对速度相关,而非转子相对于地面的绝对位移和绝对速度。

设基础相对于地面的位移矢量为xb,代入式(2),可得到用柔性转子系统在基础平动激励后用相对于地面的位移表示的动力学方程,即:

(3)

当基础相对于地面在平动方向上发生运动时:一方面只能测量转子相对于运动基础的位移,而不是转子相对于地面的位移;另一方面,转子相对于运动基础的位移远比转子相对于地面的位移更有意义。

在考虑柔性转子系统的基础受外部激励只是在平动方向上产生运动的条件下,转子相对于基础的位移矢量x为:

x=x0-xb

(4)

将式(4)代入式(3),就可以得到柔性转子系统在基础平动激励后,用相对于运动基础的位移表示的动力学方程,即:

(5)

可见,对于柔性转子系统而言,由于陀螺效应的影响,基础的平动激励不仅产生了一个与基础加速度相关的激励项,而且还出现了一个与基础速度有关的激励项。这也是基础平动激励条件下,转子系统与一般非旋转系统动力学模型上的差异。

1.3 基础平动激励条件下电磁轴承-柔性转子系统的动力学方程

对于n个节点的电磁轴承-柔性转子系统,电磁轴承只是安装在有限的节点。为方便起见,此处假设每一个节点上都安装有电磁轴承及存在不平衡力。电磁轴承对转子的作用按照一个外激励力进行处理。

电磁轴承-柔性转子系统中电磁轴承处的电磁力矢量如果采用线性化模型,则可以表示为:

FAMB=Kxx+Kii

(6)

式中:Kx—4n×4n维的电磁轴承位移刚度系数矩阵,N/m;Ki—4n×4n维的电磁轴承电流刚度系数矩阵,N/A;i—控制电流矢量,A。

Ki均为对角矩阵,对角线上的元素为各电磁轴承的位移刚度系数和电流刚度系数。

在恒速情况下,电磁轴承-柔性转子系统的转子的不平衡激励力矢量为:

Fu=εMω2sin(ωt+φ)

(7)

式中:ε—每个节点的不平衡偏心率;φ—每个节点的不平衡相位角,°。

由此,可以得到基础平动激励条件下,电磁轴承-柔性转子系统的动力学方程:

(8)

据式(8),可得到基础平动激励条件下,电磁轴承-柔性转子系统动力学方程的状态空间方程:

(9)

2 控制器设计

与传统的转子系统不同,在电磁轴承-柔性转子系统中,可以利用电磁轴承对基础平动激励导致的振动进行主动控制。

从基础平动激励条件下电磁轴承-柔性转子系统动力学方程可以发现,基础平动激励对转子系统动力学特性的影响可以等效为由基础加速度和基础速度导致的附加激励力。不平衡转子系统在基础平动激励条件下,等效的激励力不仅含有与转速同频的成分,而且还含有基础平动激励频率的成分,是一个多频激励问题[19,20]。

为了解决基础平动激励条件下,电磁轴承-柔性转子系统的振动控制,笔者提出一种基于LMS算法的,以基础加速度为参考信号的变步长自适应控制器。

2.1 基于变步长LMS算法的自适应控制器设计

基于LMS算法的自适应控制器主要包括输入信号延迟环节、权矢量矩阵以及输出信号,其结构原理图如图2所示。

图2 基于LMS算法的自适应控制器结构原理图

根据图2,输入信号as经过P个延时单元,构成控制器的参考信号S(n)为:

S(n)=[as(n)as(n-1) …as(n-p)]T

(10)

每个延时位置均有一个权系数,构成权矢量W(n)为:

W(n)=[w0w1…wp]T

(11)

控制器的输出信号out(n)为:

out(n)=WT(n)S(n)

(12)

误差信号e(n)为期望信号ε(n)与输出信号out(n)的差值,即:

e(n)=ε(n)-out(n)=ε(n)-WT(n)S(n)

(13)

自适应过程即为调节权矢量,改变输出信号out(n),使得误差信号e(n)的绝对值最小的过程。由于绝对值函数难以进行参数迭代和目标函数寻优,此处采用MSE(mean square error)为目标函数:

MSE=ξ(n)=e2(n)

(14)

目标函数的梯度为:

(15)

根据最速梯度下降法,可得到权矢量W(n)的更新公式为:

(16)

式中:μ—迭代步长。

对于定步长LMS算法而言,在保证算法收敛的情况下,步长μ越大,收敛速度越快,但也会造成稳态误差的增大;步长μ越小,稳态误差越小,但收敛速度减慢。

为解决收敛速度和稳态误差之间的矛盾,笔者利用tanh函数,提出一种变步长迭代方法:

μ=αtanh2{βe(n)}.

(17)

步长μ随不同α及β值与误差信号间的关系如图3所示。

图3 步长μ随不同α及β值与误差信号间的关系

图3中,当β不变,α越大,步长的变化范围越大;当α不变,β越大,步长随误差的变化曲线斜率越大;可通过调整α来控制步长μ的取值范围,调整β控制步长μ衰减速度。

由此可知,采用式(17)中的变步长算法,可使W(n)在误差较大时迭代步长大,速度快;在误差较小时迭代步长小,速度慢。

2.2 基于自适应控制器的基础平动激励振动抑制系统模型

基础平动激励下,基于自适应控制器的振动响应抑制系统模型如图4所示。

图4 基于自适应控制器的基础平动激励转子振动抑制系统模型加速度传感器测得的基础加速度;xE—期望位移;x—相对位移;xDS—期望位移与相对位移之差;out(n)—控制器输出信号

自适应控制器的参考信号S(n)为基础在平动方向上的加速度,即:

(18)

误差信号e(n)为:

e(n)=xE(n)-x(n)=xDS(n)

(19)

则权值更新公式为:

W(n+1)=W(n)+μxDS(n)S(n)

(20)

3 仿真及结果分析

3.1 基础平动激励条件下柔性转子系统的响应特性

仿真中使用的柔性转子模型如图5所示。

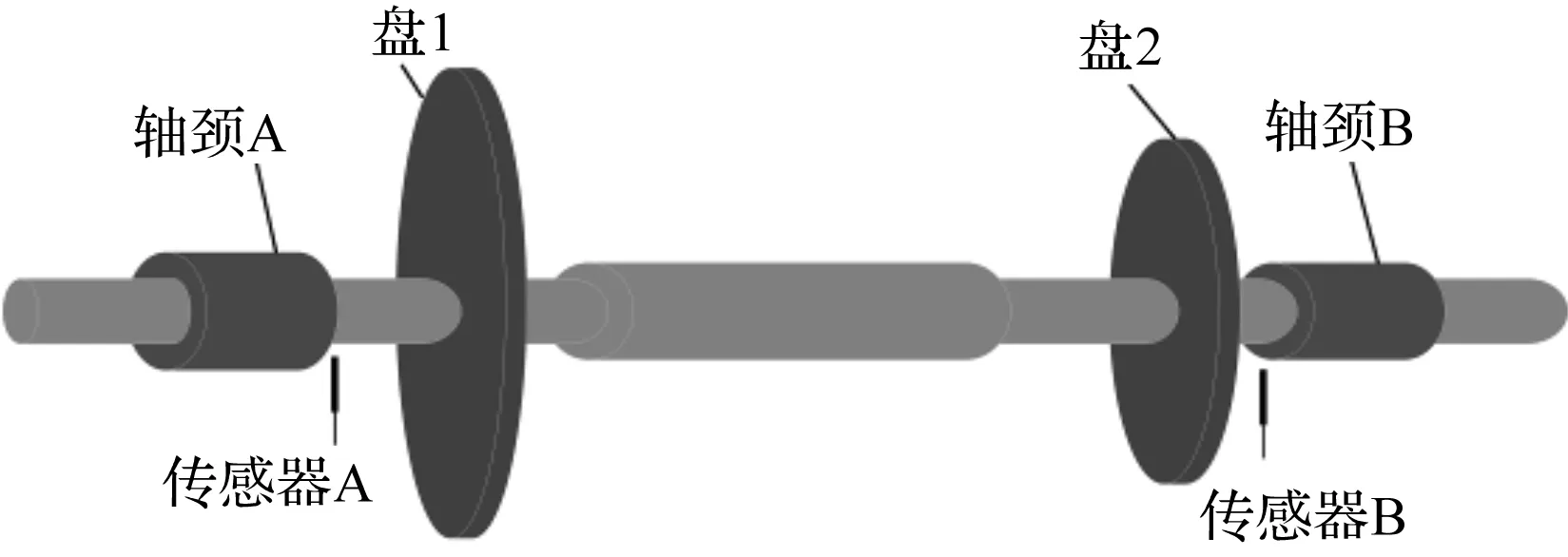
图5 仿真中使用的柔性转子模型

其中,转子的具体参数如表1所示。

表1 转子的具体参数

转子在自由状态下的刚体平动模态频率约为18 Hz,一阶弯曲模态频率约为78 Hz。调整PID控制器参数,使得柔性转子稳定运行,在水平x方向上施加等幅、不同频的正弦基础平动激励。

为简化分析,笔者不考虑传感器和执行器不同位的影响,认为传感器和电磁轴承的轴向位置重合。由于左、右两个传感器位置处转子的振动特性及变化规律相似,这里仅给出了左端传感器A处转子的计算结果。

在转子系统中,由于陀螺效应的影响,基础平动激励不仅产生了一个与基础加速度相关的激励项,还出现了一个与基础平动速度有关的激励项;基础平动速度信号由基础加速度信号处理得到。

根据得到的基础平动激励条件下电磁轴承-转子系统的状态空间方程、PID主控制器及所设计的基础平动激励控制器,笔者在MATLAB/Simulink中搭建了系统的仿真模型。

在PID主控制器下,转子的位移刚度kx为2.205×106N/m,电流刚度ki为716.2 N/A。

当转子转速为6 000 r/min时,笔者在基础的x方向施加幅值Ab为5 m·s-2、频率fb为5 Hz、相位为0的单频正弦基础平动激励。

传感器A处转子的运动轨迹如图6所示。

图6 传感器A处转子的运动轨迹

由图6的转子运动轨迹可见,当在基础的x方向施加基础平动激励时,转子在激励方向上的振动明显增大,而对在非激励的y方向的振动几乎没有影响。

3.2 转子振动响应与基础平动激励频率的变化关系

给基础施加不同频率、幅值相等(5 m·s-2)、相位为0的基础平动激励,激励频率对电磁轴承-柔性转子系统传感器A处转子振动响应特性曲线的影响,如图7所示(图7中的曲线为转子在无基础平动激励情况下的位移响应曲线)。

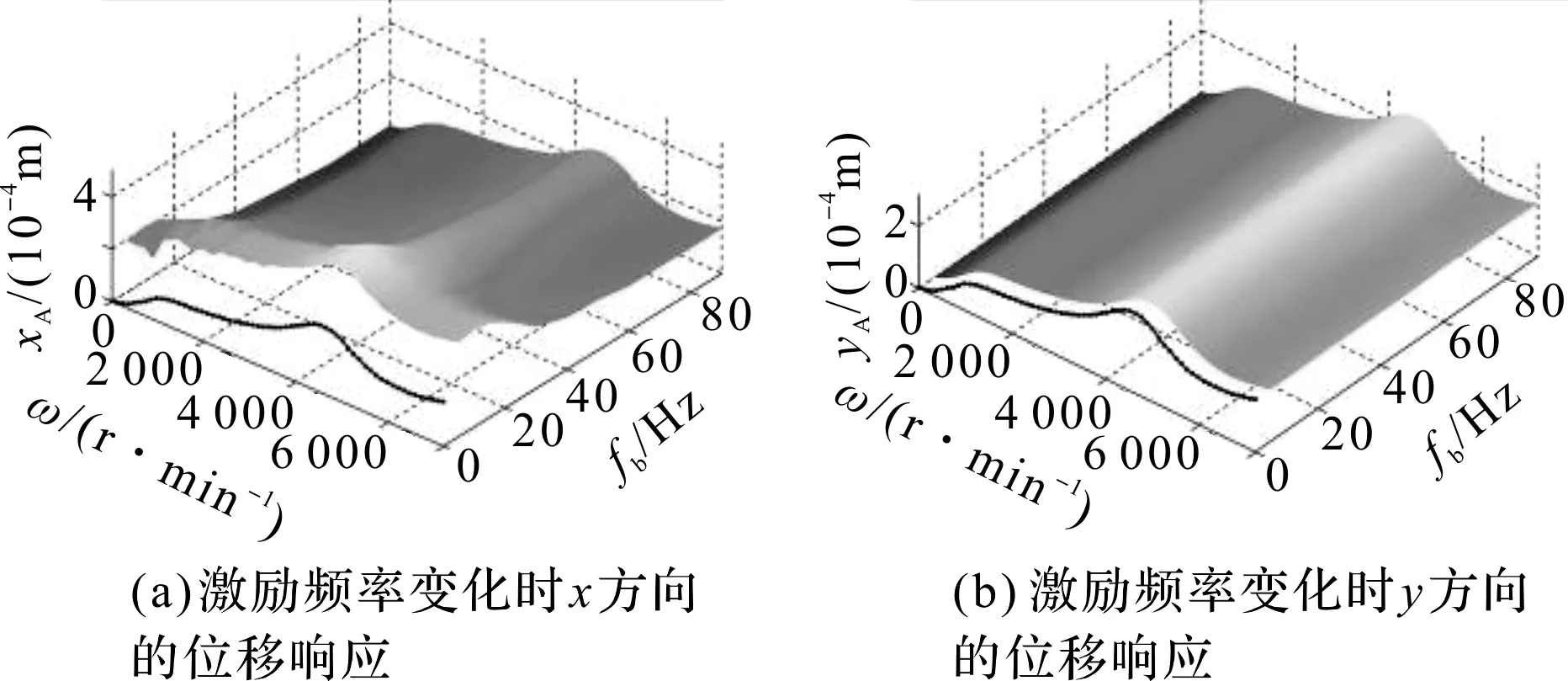
图7 激励频率对电磁轴承-柔性转子系统传感器A处转子振动响应特性曲线的影响

根据图7(b)可知:基础平动激励频率的改变不会导致非施加基础平动激励方向上转子振动的变化。

与3.2其他条件相同的情况下,在基础水平方向上施加不同幅值、频率相同(5 Hz)、相位为0的正弦平动激励,可得到不同激励幅值下传感器A处转子的振动位移响应特性曲线,如图8所示。

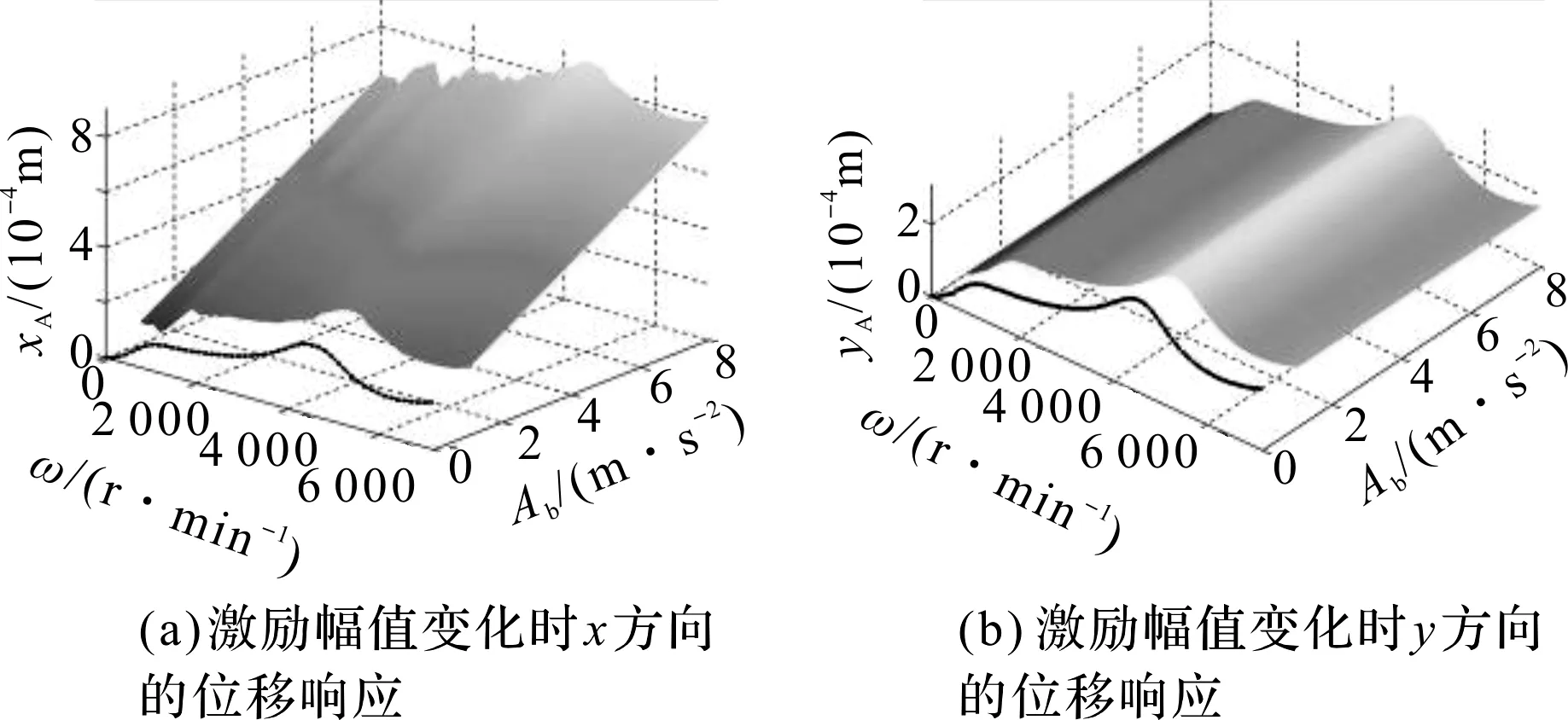
图8 不同激励幅值下传感器A处转子的振动位移响应特性曲线

根据图8(a)可知:在整个转速范围内,当基础平动激励的频率不变时,施加基础平动激励方向上转子的振动响应幅值随平动激励幅值的增大而增大;

根据图8(b)可知:激励幅值的改变不会导致非施加基础平动激励方向上转子位移响应的变化。

在其他条件相同的情况下,在基础水平方向上施加幅值和频率相同(5 m·s-2,5 Hz)、相位不同的正弦平动激励,可得到不同相位差下传感器A处转子的振动响应曲线,如图9所示。

图9 不同相位差下传感器A处转子的振动响应曲线

根据图9(a)可知:在刚体临界转速附近时,相同转速下相位的改变会引起较大的转子振幅波动;而在一阶弯曲临界转速附近时,相同转速下转子振幅几乎不随激励相位的改变而改变。

由此,将转子设定在不同转速(刚体临界转速之下,刚体临界转速和一阶弯曲临界转速之间,一阶弯曲临界转速之上)下,保持基础平动激励的幅值、频率不变,只改变激励的相位,可得到不同转速频率下传感器A处转子的振动幅值和激励相位的变化结果,如图10所示。

图10 不同转速频率下传感器A处转子的振动幅值和激励相位的变化结果

结合图9和图10可知:当基础平动激励频率较低,与旋转频率相差不大时,激励相位的改变会引起较大的振幅波动;当旋转频率与基础平动激励频率相差较大时,激励相位的改变对转子振动响应的影响较小;激励相位的改变不会导致非施加基础平动激励方向上转子位移响应的变化。

综上所述:基础平动激励仅对转子在激励方向上的位移产生影响,不会影响与其垂直方向上的位移响应;当激励频率较低,且幅值较大时,转子的最大位移响应幅值远大于基础静止状态下的幅值,这时如果不施加必要的控制,转子极易与备用轴承发生碰撞,甚至导致系统失稳。

3.3 基础平动激励下柔性转子的振动抑制

3.3.1 单频正弦激励时柔性转子的振动抑制

对转子施加频率为5 Hz、幅值为5 m·s-2、相位为0的正弦基础平动激励,可得到无基础平动激励、有基础平动激励和对基础的平动激励进行控制后传感器A处转子振动响应结果,如图11所示。

图11 无基础平动激励、有基础平动激励和对基础的平动激励进行控制后传感器A处转子振动响应

由图11可知:在无基础平动激励时,传感器A处转子振动响应的最大幅值出现在转子的一阶弯曲临界转速附近;当基础受到单频平动激励时,传感器A处转子的振动基本上按照一个常增量增大,这是因为整个转子系统为线性系统,其振动响应为基础平动激励和不平衡激励的叠加,转速的变化会带来不平衡激励的变化;而式(8)中,陀螺效应项相对于阻尼项很小,基础平动激励所引起的转子振动分量几乎不会使振动位移基本按照常增量增大;最大幅值出现在转子的一阶弯曲临界转速附近,最大振幅约为0.5 mm,由于一般的电磁轴承转子系统备用支承的间隙不会超过0.5 mm,基础平动激励可能会导致转子与备用轴承相碰。

在使用了自适应控制后,转子的位移迅速减小,并接近无基础平动激励条件下转子振动响应曲线。可见采用自适应控制时,在整个转速范围内都十分有效。

3.3.2 多频正弦激励时柔性转子的振动抑制

为验证自适应控制器对多频激励的控制效果,笔者再施加包含5 Hz、10 Hz、15 Hz频率分量的多频基础平动激励,其幅值分别为5 m·s-2、2 m·s-2、1 m·s-2,相位均为0,得到无基础平动激励、多频基础平动激励和对基础的平动激励进行控制后传感器A处转子振动响应结果,如图12所示。

图12 无基础平动激励、多频基础平动激励和对基础的平动激励进行控制后传感器A处转子振动响应

由图12可知:当基础受到多频平动激励时,传感器A处转子的振动也基本上按照一个常增量增大,多频基础平动激励条件下振幅的常增量比单频基础平动激励条件下振幅的常增量大,最大幅值同样出现在转子的一阶弯曲临界转速附近,最大振幅约为0.8 mm,所以基础平动激励将会导致转子与备用轴承相碰,使系统不能正常工作;

在使用了自适应控制后,转子位移迅速减小,并接近无基础平动激励条件下转子振动响应曲线。可见采用自适应控制时,在整个转速范围内都十分有效。

笔者将转子设定在6 000 r/min稳定转速下,施加多频基础平动激励,并开启自适应控制。

在开启自适应控制前后,传感器A处转子位移响应的FFT分析结果如图13所示。

图13 控制前后传感器A处转子位移响应的FFT分析结果

将全转速范围内基础平动激励自适应控制前后转子振动响应的控制效果和图13进行对比可知:

(1)所设计的基于LMS算法的变步长自适应控制器可以有效地抑制基础单频及多频平动激励对转子振动位移的影响;

(2)根据3.2中的结论和实际情况下转子运行转速较高,旋转频率与基础平动激励频率差值较大的情况,因此不考虑二者频率相同的情况。

4 结束语

在基础平动激励条件下,笔者首先建立了电磁轴承-柔性转子的动力学方程及状态空间模型;然后基于LMS算法,设计了变步长自适应控制器;最后,利用MATLAB/Simulink仿真工具,分析了在PID主控器下全转速范围内电磁轴承-柔性转子系统在基础平动激励条件下的振动特性,验证了所设计的自适应控制器在基础平动激励条件下,对电磁轴承-柔性转子系统振动的控制效果,得到如下结论:

(1)基础平动激励仅对激励方向上转子的振动产生影响,不会影响与其垂直方向上转子的振动;基础平动激励的频率越低,转子的振动越大,基础平动激励的频率越高,转子的振动越小;转子在基础平动激励方向上的振动随平动激励幅值的增大而增大;

(2)当转子的转速较低,基础平动激励与不平衡激励力的相位相差不大时,基础平动激励相位的改变会引起较大的转子振幅波动;当转子的转速较高,基础平动激励与不平衡激励力的相位相差较大时,基础平动激励相位的改变对转子振动的影响较小;

(3)所设计的基于LMS算法的变步长自适应控制器,能够有效地抑制基础单频及多频平动激励对转子振动的影响,使转子的振动接近无基础平动激励时的水平。