弹簧成形机几何误差的完备建模及其补偿方法研究*

刘晓肖,王德成,程 鹏,邵晨曦,李 伟

(1.机械科学研究总院,中机生产力促进中心,北京,100044;2.机械科学研究总院,北京,100044)

0 引 言

弹簧作为通用零件,在各行业中发挥着重要的作用[1]。弹簧质量的提升可以使我国工业水平有所提高,而弹簧成形机的精度则直接影响弹簧成形质量。

在实际生产中,不同精度等级弹簧成形机成形的弹簧尺寸波动大,导致弹簧服役性能不稳定。因此,弹簧成形机的误差不可忽略。弹簧成形机误差包括几何误差、系统误差、力误差等多种误差,根据杨建国团队[2]的研究表明:几何误差占据机床总误差的30%～45%。研究弹簧成形机几何误差对提高弹簧成形尺寸精度具有重要工程价值与现实意义。目前,弹簧成形机精度控制的方法有采用高精度装配零部件和定期检修两种,这两种方法均未对弹簧成形机几何误差进行研究,无法得到单独、系统的弹簧成形机精度规律及方法。

关于几何误差的研究主要分为:几何误差建模方法、几何误差识别与测量方法、误差补偿方法3个方面。具体分述如下:

(1)针对不同类别的数控机床几何建模方法有:基于多体系统理论的数控机床几何误差模型建立方法[3,4]、基于参数化建模的几何误差快速辨识方法[5]1以及有限元法[6]。对此,国内外研究者都进行了相关研究:国外的主要研究有:XIA Chang-jiu等人[7]基于单轴运动测量,采用多提系统理论建模的方式,避免了非目标轴的干扰,提高了识别精度。徐凯等人[5]9基于参数化建模方法,建立了旋转轴几何误差快速辨识模型。单轴运动方式与弹簧成形机工作方式类似,该方法可用于弹簧成形机单轴测试与模型建立。VAHEBI M等[8]考虑了三轴机床拓扑结构对空间误差的影响,运用齐次坐标矩阵变换,建立了三轴数控机床空间误差模型,并通过球杆仪测试机床两轴联动圆度误差,验证了模型的准确性。国内主要研究有:天津大学刘又午教授[9]采用了低序体阵列来描述多体系统结构,使多体系统理论的表述方式更为简洁、直观。国防科技大学李圣怡教授等人[10]推导出了一套统一的几何误差模型表达式,适用于各类配置的多轴机床,进一步推动了多体系统理论的发展。多体系统理论建模简单,包含的参数数量没有限制,适用于弹簧成形机的建模;

(2)几何误差测量分为直接测量[11，12]和间接测量[13]。直接测量多采用激光测量的方式,如文献[12]提出了一种高效、直接、高精度机床误差的新型激光测试方法,该方法的测试精度可达6.3 nm。直接测量适用于中小型机床,间接测量适用于大型机床;直接测量方法的测量精度比间接测量差,但直接测量操作简单、经济性高。结合弹簧成形机的特点,将直接测量用于弹簧成形机几何误差测量更为合理;

(3)误差补偿方法分为在线实时误差补偿[14,15]和离线误差补偿[16,17]两种。弹簧成形机自动化程度不高,离线误差补偿更具有实际工程意义。

综上所述,本文将采用多体系统理论建立弹簧成形机几何误差完备模型,并以此为理论基础研究提升弹簧成形机成形精度的方法,填补弹簧成形机精度研究方法的空白。

1 弹簧成形机几何误差

1.1 弹簧成形机几何误差元素定义

多工位弹簧成形机通过装配不同的刀具,组合成不同的成形机多体系统,可实现不同种类弹簧的成形。尽管弹簧的种类很多,但所有弹簧的结构特征都可以拆分为:折角、圆弧和螺旋线。

弹簧成形过程是多轴联动制造过程,各刀具轴分别以规定角度安装在成形机背板上,每把成形刀依次成形一个弹簧特征,最终实现空间弹簧成形。

曲线规成形弹簧圆弧,送线轴实现钢丝直线运动,节距刀成形弹簧节距,曲线规与节距刀联动成形空间螺旋线,多轴联动可实现空间弹簧成形。

弹簧成形机结构如图1所示。

图1 弹簧成形机结构简图0—成形机机身;1—曲线规刀架轴;2—曲线规;3—节距刀刀架轴;4—节距刀;5—芯轴;6—钢丝

弹簧成形机的几何误差包括:曲线规的装配误差、定位误差;节距刀的装配误差、定位误差和折角刀的装配误差、定位误差。所有几何误差最后集中反映为成形刀具成形点的位置误差。因此,此处以刀具成形点为检测对象,建立刀具成形点几何误差模型。

笔者将刀具的几何误差沿X、Y、Z3个方向定义,各刀具的几何误差分别包括沿X、Y、Z3个方向的平动误差和绕X、Y、Z3个轴的转动误差。

以沿X轴进给为例,其几何误差元素如图2所示。

图2 沿X轴进给6项几何误差元素

芯轴的旋转轴线与X、Y存在位置误差,根据弹簧成形特征,此处不考虑各轴之间垂直度误差。

因此,满足弹簧基本形状特征的弹簧成形机共包含20项空间几何误差,如表1所示。

表1 弹簧成形机空间几何误差

1.2 弹簧成形机运动链拓扑描述

将弹簧成形机视作多体系统,依据多体系统理论对弹簧成形机进行拓扑结构描述。当m为k的n阶低序体时,Ln(k)=m。另外规定:k的零阶低序体为k,L0(k)=k;LN(0)=0,参考系默认为部件0。

根据多体系统理论将成形机机身视为惯性体,编号为0,并按照钢丝运动链与成形刀运动链依次对运动部件进行编号。曲线规刀具链为:成形机机身0—曲线规刀架轴1—曲线规2;节距刀刀具链为:成形机机身0—节距刀刀架轴3—节距刀4;钢丝运动链为:成形机机身0—芯轴5—钢丝6。

根据弹簧特征建立拓扑结构简图如图3所示。

图3 弹簧成形机拓扑结构图

圆弧特征成形机多体系统低序体阵列如表2所示。

表2 圆弧特征成形机多体系统低序体阵列

螺旋线特征成形机多体系统低序体阵列如表3所示。

表3 螺旋线特征成形机多体系统低序体阵列

2 几何误差完备建模

在多体系统理论中,体间实际位置关系取决于二者初始位置、相对运动关系及其对应误差[18]。由此可知,体k与其相邻低序体m之间的实际位置关系特征矩阵Tmk可表示为:

Tmk=Tmk,pTmk,peTmk,sTmk,se

(1)

式中:Tmk,p—低序体m相对于k的初始位置特征矩阵;Tmk,pe—低序体m相对于k的位置误差特征矩阵;Tmk,s—低序体m相对于k的理想运动特征矩阵;Tmk,se—低序体m相对于k的运动误差特征矩阵。

各运动链相邻低序体的特征矩阵如表4所示。

表4 弹簧成形机相邻低序体体间特征矩阵

在刀具坐标系Ot下,各成形刀具坐标点为Pt=[xt,yt,zt,1]T;在钢丝坐标系Ow下,钢丝成形坐标点为Pw=[xw,yw,zw,1]T。通过建立运动链可将刀具成形点与钢丝成形点转换到成形机惯性坐标系O0下。成形时,刀具成形点坐标与钢丝坐标应重合,即:

(2)

(3)

(4)

根据成形原理可知,在惯性坐标系下,刀具成形点坐标位置为实际成形位置。

圆弧特征、螺旋线特征对应的成形刀几何误差完备模型Earc、Epit如下所示:

(5)

[(T03T34)-1(T05T56)-(T03,pT03,sT34,pT34,s)-1

(T05,pT05,sT56,pT56,s)]Pw

(6)

3 Sobol灵敏度分析

3.1 Sobol方法原理

弹簧成形机几何误差完备模型包括20项几何误差,具有参数多、模型复杂的特点。以弹簧成形机几何误差完备模型为理论依据,展开成形精度监控的难度大,误差补偿效果不明显。需要针对几何误差完备模型进行灵敏度分析,识别出对成形精度影响较大的关键误差项,便于后续成形精度监控及误差补偿。

本文采用Sobol灵敏度分析方法,对各几何误差进行分析。各误差项的灵敏度系数能够直观地量化该误差项对成形精度的影响权重,适用于弹簧成形机关键几何误差项的识别。

Sobol灵敏度分析方法属于基于方差分解形式的全局灵敏度分析法,采用各输入量对应函数值的方差与误差模型总方差的比值来评价相应输入量的灵敏度系数[19]。

将弹簧成形机的几何误差模型表达为Y=f(h)。其中,h—几何误差项,h=(h1,h2,...hn),n—误差项的个数。根据误差项个数n定义一个n维的单元体Rn,作为输入参数的空间域,即:

Rn=(hi|vmin≤hi≤vmax,i=1,2,…,n)

(7)

式中:vmin—误差项区间下限;vmax—误差项区间上限。

首先依据弹簧成形机最大加工外径尺寸确定各刀具轴进给范围,然后在进给范围内使用带磁力表座的千分表对成形机各轴的几何误差进行检测,具体的测量现场实物图如图4所示。

图4 带磁力表座千分表测量几何误差现场图

由于成形刀具固定在机床导轨上,要求导轨与背板无安装间隙,刀具沿导轨移动,曲线规在Z轴方向的移动误差与转动误差按照背板、导轨加工误差进行设置。

通过对弹簧成形机20项几何误差进行测量,可确定各误差项的采样区间范围,如表5所示。

表5 20项几何误差取值范围

将Y=f(h)按照Sobol方法分解为递增阶数的形式[20],即:

(8)

Y0=E(Y)

(9)

Yi=Eh～i(Y|hi)-E(Y)

(10)

Yij=Eh～ij(Y|hi,hj)-Yi-Yj-E(Y)

(11)

式中:Y0—对应输入参数的整体模型的期望值;Yi—第i个误差项hi对应的函数值;Yij—误差项hi和hj共同作用下所对应的函数值;hi—第i个误差项;h～i—除第i个误差项外的所有误差项;h～ij—除第i个和第j个误差项外的所有误差项。

对式(8)进行方差计算,可得:

(12)

对式(12)除以函数总方差V,再进行正交化,可得:

(13)

(14)

(15)

(16)

式中的一阶方差比值Si称作误差项hi的一阶灵敏度系数;用Si衡量输入量hi对模型输出总体方差V的影响权重;Si值越大,hi对输出方差的影响程度越大。

二阶方差比值Sij表示误差项hi和hj(i≠j)耦合作用时所对应的灵敏度系数;Sij值越大,说明误差项hi和hj之间的耦合作用越明显。

STi为总体灵敏度系数。用STi评估模型中各误差项之间的耦合关系。其物理意义为hi的一阶灵敏度系数Si和所有与hi有耦合作用的高阶灵敏度系数之和。

3.2 Monte carlo估算

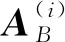
综上所述,可得Monte Carlo估算公式如下:

(17)

(18)

(19)

(20)

式中:k—误差项的采样个数;n—误差项的个数;m—相应采样矩阵的第m行。

灵敏度系数的估算公式如下:

(21)

(22)

3.3 关键几何误差项识别

此处选取弹簧成形机行程为:曲线规进给50 mm,节距刀进给10 mm,芯轴旋转90°形成折角作为研究对象进行灵敏度分析,研究20项几何误差对成形精度的影响规律。

采用MATLAB计算,得到针对圆弧特征、螺旋线特征的几何误差项灵敏度系数。其中,曲线规X方向进给运动误差项各阶灵敏度系数,如表6所示。

表6 曲线规X方向进给运动误差项各阶灵敏度系数

节距刀Y方向进给运动误差项各阶灵敏度系数如表7所示。

表7 节距刀Y方向进给运动误差项各阶灵敏度系数

由表中数据可以看出:一阶灵敏度系数Si与总体灵敏度系数ST基本一致。这说明几何误差项之间耦合作用很小,可以忽略不计,在监测与补偿时仅考虑单项几何误差即可。

一阶灵敏度系数之和接近1但小于1,与理论公式相符合。每项几何误差影响权重均值约等于0.08,考虑补偿效果,笔者选取影响权重4倍(即0.3)作为衡量灵敏度系数的阈值,作为判断某几何误差项是否为关键误差项标准。

灵敏度系数柱状图如图5所示。

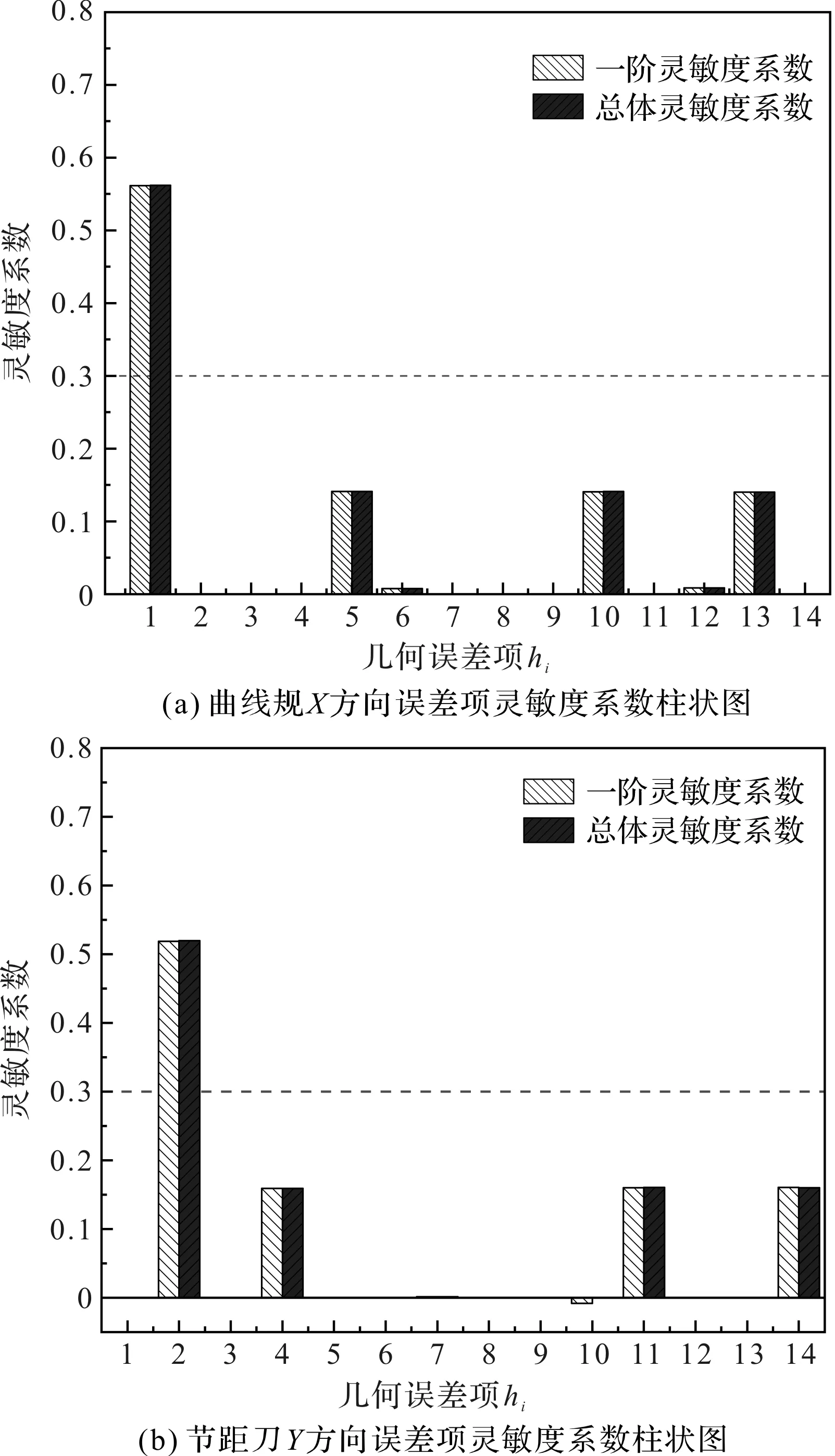
图5 几何误差灵敏度系数柱状图

由图5可知:在成形圆弧特征时,δx(x)、εy(x)、εx(z)、φxz一阶灵敏度系数和总体灵敏度系数较大,δx(x)大于0.3,属于关键误差项;在成形折角特征时,δy(y)、εx(y)、εy(z)、φyz一阶灵敏度系数和总体灵敏度系数较大,其中δy(y)大于0.3,属于关键误差项。

在曲线规成形过程中,曲线规仅沿X方向移动一个自由度。依据灵敏度分析结果,选取曲线规刀具X方向进给运动定位误差δx(x)进行误差补偿,验证该误差识别方法在弹簧成形机的实用性。

4 误差补偿

在实际生产过程中,常以曲线规沿X方向进给运动为例进行试验验证,曲线规进给行程极限为50 mm。为使试验更具有代表性和实用性,笔者试验选取曲线规极限进给行程50 mm和实际生产最常用的进给行程30 mm两个行程进行试验;弹簧刀具行程通过设定相应的脉冲值进行调节。

试验采用一级标准量块进行误差标定,用带磁力表座千分表分别测量曲线规极限进给行程50 mm和进给行程30 mm的刀具定位误差与重复定位误差。

刀具定位误差测量曲线如图6所示。

图6 曲线规定位误差

由图6可以看出:在曲线规运行至成形极限位置50 mm时,定位误差约为0.3 mm,误差较大,且为单边误差,需要进行误差补偿,以提高曲线规的定位精度。

针对曲线规进给行程50 mm的定位误差,此处采用脉冲值补偿方法,基于PMAC系统进行误差补偿。首先,以曲线规定位误差测量值的平均值作为补偿基准;然后,进行相应脉冲值的换算,得到需要进行补偿的脉冲值的大小;最后,将脉冲值输入系统,实现对弹簧刀具的定位误差补偿。

具体的换算过程如表8所示。

表8 误差补偿表

根据误差补偿换算表对刀具定位误差进行补偿,重复测量补偿后的进给行程为50 mm的曲线规定位误差10次。

补偿前后曲线规定位误差的统计如图7所示。

图7 补偿前后曲线规定位误差对比

由图7可以看出:曲线规运行至50 mm的定位误差整体减小,弹簧刀具运行稳定;经过补偿后,曲线规定位精度提高44.6%,曲线规定位位置更加接近设定值,成形弹簧尺寸更接近公称值;该结果使得一批次弹簧尺寸更加集中地分布在公称值附近,弹簧尺寸更加稳定,超差率降低。

5 结束语

本研究采用几何误差建模,对弹簧成形机的成形误差进行了研究;通过Sobol灵敏度分析方法,筛选出关键误差项,在此基础上使用基于PMAC系统的脉冲值误差补偿方法进行了误差补偿,研究得到的结论如下:

(1)以弹簧成形机为研究对象,针对目前弹簧成形机成形精度不高问题进行了研究;基于弹簧形状特征定义、识别出了20项刀具空间几何误差,采用多体系统理论与坐标变换方法,建立了弹簧成形机几何误差完备模型,填补了弹簧成形机几何误差建模与测量的空白;

(2)根据成形机几何误差完备模型,采用Sobol灵敏度分析方法,识别出了影响弹簧特征成形尺寸精度的关键误差项为各刀具的定位误差,为针对性误差补偿提供了理论依据;同时,提高了误差补偿的精确性和效率;

(3)针对成形刀具定位误差,采用基于PMAC系统的脉冲值误差补偿方法进行了补偿,选取成形刀具定位误差均值进行了伺服电机脉冲值换算,通过伺服电机补偿了成形刀具进给运动;补偿后,成形刀具定位精度提高了44.6%,验证该几何误差识别、补偿方法适用于弹簧成形机,为弹簧成形机精度提高及稳健设计提供了理论方法和思路。

笔者后续将有：(1)建立弹簧精度评价指标，对弹簧成形机成形精度进行验证与评价;(2)以弹簧几何误差建模与补偿方法为研究基础，进行弹簧成形机的在线实时监测技术研究。