基于色彩均匀敏感度的磨削表面粗糙度测量*

杨 晨,方红萍,邹凌云,伍世虔

(1.武汉科技大学 信息科学与工程学院,湖北 武汉 430081;2.南昌工程学院 机械与电气工程学院,江西 南昌 330099)

0 引 言

粗糙度是机械表面加工领域中的一个重要精度指标[1]。基于机器视觉的粗糙度测量方法具有非接触、效率高、成本低等优点,是目前粗糙度测量领域的一个研究热点[2- 4]。

传统的基于机器视觉的表面粗糙度测量,大多针对粗糙表面灰度图像,提取图像纹理特征,通过建立灰度图像纹理与粗糙度的相关性来实现表面粗糙度测量[5]。比如,SHIRINZADEH B等人[6]提出了ITC模型,认为工件表面高度形貌的归一化值与图像中对应位置的像素强度有线性关系,能够对一定粗糙度范围工件进行预测。HUYNH V M[7]从表面纹理的傅里叶变换图中提取均方根,建立了与表面粗糙度的关系。GADELMAWLA E S[8]580-588通过灰度共生矩阵的4个参数对表面粗糙度进行了评价,并讨论了这些参数对粗糙度变化的敏感性。上述方法对表面纹理明显、粗糙度大的车削、镗削等加工表面的粗糙度测量效果明显。磨削加工表面特有的加工方式,使其具有纹理弱、粗糙度低等特点,存在表面纹理特征提取困难的问题,采用上述方法的测量效果并不理想。

针对磨削加工表面弱纹理特性,近几年一些学者基于光反射原理,利用颜色信息强灵敏性、信息丰富等特点,采集彩色光在磨削表面形成的反射图像,提取反射图像的相关特征来建立与粗糙度的相关性。比如YI Huai-an等人[9]提出了基于RGB颜色空间三基色之间的色差算法与彩色图像分解算法,设计了图像清晰度指标并建立了该指标与粗糙度相应的关系模型。LU En-hui等人[10]96-98构建了基于彩色图像的能量统计学矩阵,设计了混叠区域重合度指标Scy,实现了粗糙度测量。然而,现有的反射光图像粗糙度测量方案,一般只考虑通过不同颜色的色彩差异设计指标,忽略了磨削表面存在的特有弱纹理方向对彩色光混叠效应的影响。

本论文针对磨削加工表面弱纹理特点,将磨削加工表面作为反射镜面,基于Beckmann-Spizzichino光反射模型,提出一种基于彩色光反射图像的磨削表面粗糙度测量方案,并分析设计机理,搭建磨削表面粗糙度测量平台;同时,结合磨削表面存在的特定弱纹理方向特性,设计出一种与磨削表面粗糙度有强相关性的色彩均匀敏感度指标Cusd,实现对磨削表面的粗糙度测量。

1 磨削表面粗糙度测量方案

1.1 Beckmann-Spizzichino反射模型

Beckmann-Spizzichino模型[11](简称BS模型)是一种基于基尔霍夫假设,描述光在不同粗糙度表面的物理反射率模型。BS模型定义的反射面辐射度包含两个部分,即镜面脉冲分量(反射部分)和镜面波瓣分量(漫反射部分)。

NAYAR S K[12]614-617基于BS反射率模型开展仿真实验,在粗糙度分别为0.002 μm、0.05 μm、0.5 μm的3种粗糙面,观察光入射角度θi分别为0°、15°、30°……90°时,辐射度Lr与反射角θr的关系曲线,即Lrθi(θr)如图1所示[12]622。

图1 BS反射率模型仿真实验结果[12]622

分析图1得出结论:当入射角θi相同的情况下,随着反射面粗糙度的增加,漫反射分量逐渐增加,辐射度Lr逐渐不再集中,曲线大致呈现正态分布状态,出现反射光向两边扩散的现象。比如,图1(a)中Ra=0.002 μm,镜面反射分量占主导,反射光基本呈现尖峰状态;图1(b)中粗糙度有所增加,但反射光大部分仍然为镜面反射,反射方向基本集中;图1(c)中粗糙度进一步增加,辐射能量中的漫反射开始占主导,反射光明显呈现向两边扩散的现象。

1.2 测量机理分析

基于上述分析可知,反射光辐射度Lr与粗糙表面的粗糙度有较强的相关性。如何有效地度量反射光辐射度Lr是实现粗糙度度量的关键。本研究基于BS反射模型,给出一种基于彩色光反射图的磨削表面粗糙度测量方案:

将磨削表面作为光源反射面,通过相机成像获取反射光图像Iim。基于机器视觉成像原理[13]可知,反射光图像Iim的照度与粗糙面反射光辐射度Lr成正比,可通过反射光图像Iim与粗糙度关联。

如图2所示,本文采用LU En-hui等人[10]102设计的红绿彩色光源,将两束平行光源作为入射光,经磨削表面反射获取反射光图像Iim。

图2 红绿光源

磨削表面粗糙度越低,产生的漫反射成分越少,两束反射光在反射图像中不易产生明显混叠。而对于粗糙度较高的表面,两束平行光均会由于漫反射成分的增加,产生反射区域扩散,从而在反射图Iim中呈现反射光混叠的状况,且这种混叠效应随着粗糙度的增加而逐渐增强。

图3是以不同磨削粗糙表面为反射面,采集到的反射图像。随着粗糙度(本文粗糙度为Ra,单位为μm)从0.01 μm增加到0.606 μm,平行的红光和绿光中间产生的混叠效应逐渐明显,边界逐渐模糊。

图3 不同粗糙表面反射图像混叠情况对比

另外,磨削加工表面弱纹理还具有特定方向的特性。入射光相同,不同纹理方向产生的反射光的方向也不一样。该特性对粗糙度的测量精度会有影响[14]。

纹理方向对反射光的影响如图4所示。

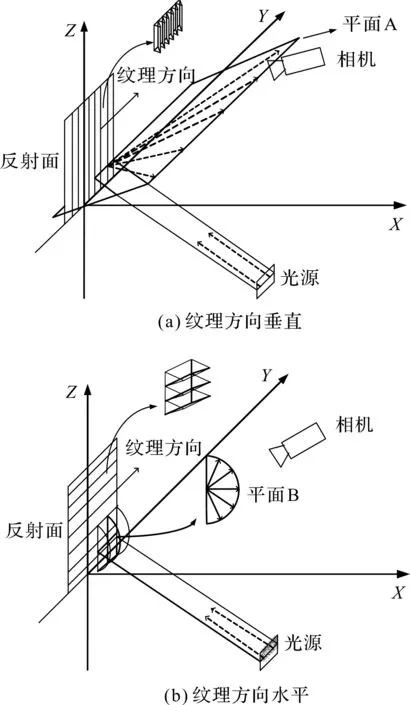
图4 纹理方向对反射光的影响

将纹理方向竖直的样块、相机和光源置于X-Z平面,假设入射光为红绿光源中间光线,其既有绿光也有红光。图4(a)中,红绿色入射光经垂直纹理方向的磨削表面反射后,反射光以平面A所示,向两边扩散,不易造成平行的红绿光产生混叠。图4(b)中,红绿色入射光经水平纹理方向的磨削表面反射后,反射光以平面B所示,向上、下方向扩散,则红绿光混叠程度明显增强。因此,磨削表面的反射光混叠程度受两个因素的影响:(1)磨削表面的粗糙度;(2)磨削表面的纹理方向。

笔者通过实验,进一步探讨这一现象。实验中,入射光角度固定,通过旋转样块(旋转角度记为θ)来模拟不同纹理方向磨削表面。

粗糙度为0.01 μm、0.384 μm、0.731 μm的磨削表面在旋转15°、45°、75°时的混叠效应影响图，如图5所示。

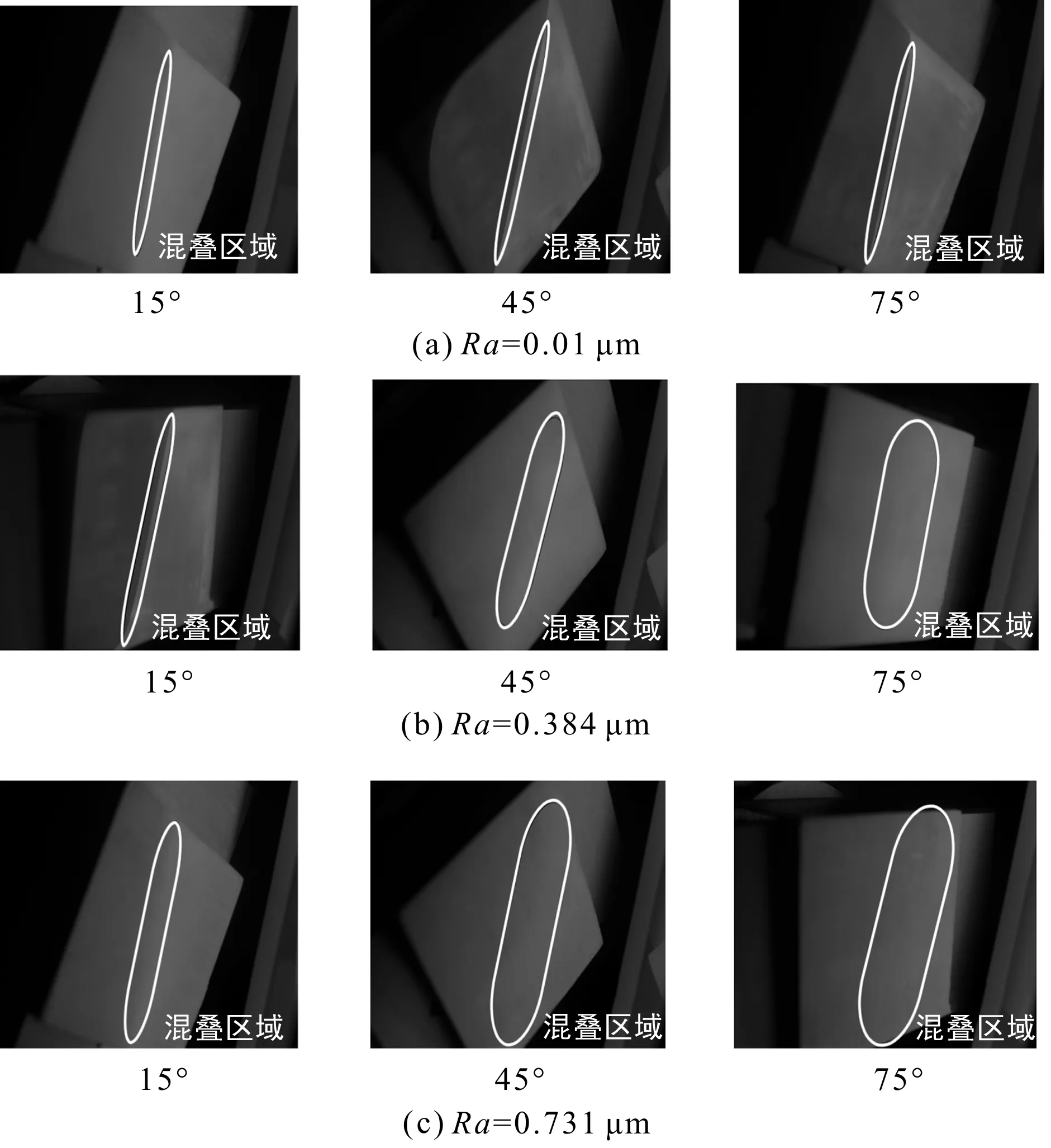
图5 纹理方向对混叠效应的影响

如图5所示:(1)在同一旋转角度(即同一纹理方向),随着表面粗糙度从0.01 μm到0,731 μm,红绿光的混叠效应越明显。说明粗糙度越大,混叠效应越明显;(2)在同一糙度表面,粗糙表面纹理方向对混叠程度也有影响,粗糙度为0.01 μm时,混叠区域的影响较小;当粗糙度分别为0.384 μm和0.731 μm时,在不同旋转角度,混叠效应均有明显变化;在粗糙度更高的0.731 μm表面,角度变化对混叠效应的影响更明显。说明粗糙度越大,反射光的混叠程度对表面纹理方向变化的敏感程度越明显。

鉴于此,笔者通过旋转磨削表面来模拟不同纹理方向,提取反射光图像中在各种不同旋转角度下彩色光混叠程度,描述反射面混叠程度对表面纹理方向的敏感度,建立与粗糙度特性的强关联特性。

1.3 粗糙度测量实验平台搭建

笔者搭建的磨削表面粗糙度测量实验平台如图6所示。

图6 粗糙度测量实验平台

实验平台主要包含如下几个部分:

(1)磨削表面作为反射面由夹具固定,与工作台保持45°夹角,为了更好地捕捉效果,相机光轴与磨削样块也呈45°;

(2)夹具可以旋转磨削表面,调整旋转角θ,以便从反射图像中获取反映不同入射光混叠程度的敏感指标;

(3)光源由台架固定,垂直于工作台面,调整光源高度,保证入射角为45°;

(4)相机为500万像素的大华CCD,负责采集反射光图像;

(5)其余设备包含光源控制器、粗糙度测量仪,及PC机等。为避免环境光的影响,实验应在暗室中进行。

2 反射光图像粗糙度测量指标

从上述测量方案中,选取红光和绿光两束平行光入射到磨削表面。当磨削表面粗糙度逐渐增大时,两束平行的红光和绿光的交界处会发生明显的红色和绿色反射光混叠现象。鉴于此,需要设计一个合适的指标去量化这种混叠效应。

色彩均匀度(Color Uniformity)是CIE Luv颜色空间中用来量化图像中各个颜色均匀性的指标,适用于加色混合产生色彩的表示与计算。

色彩均匀度计算如下:

(1)

利用色彩均匀度去度量反射光图像中心区域的混叠程度。由于混叠主要集中在反射光图像的中心部分,靠近中心区域的采样点密度应该更大[15]。图像M个采样点的采集方案如图7:圆心位于图像中心,将采集图像边长作为圆的直径,将圆分为36个小块,采样点从每个小块中随机选取一个,共36个。

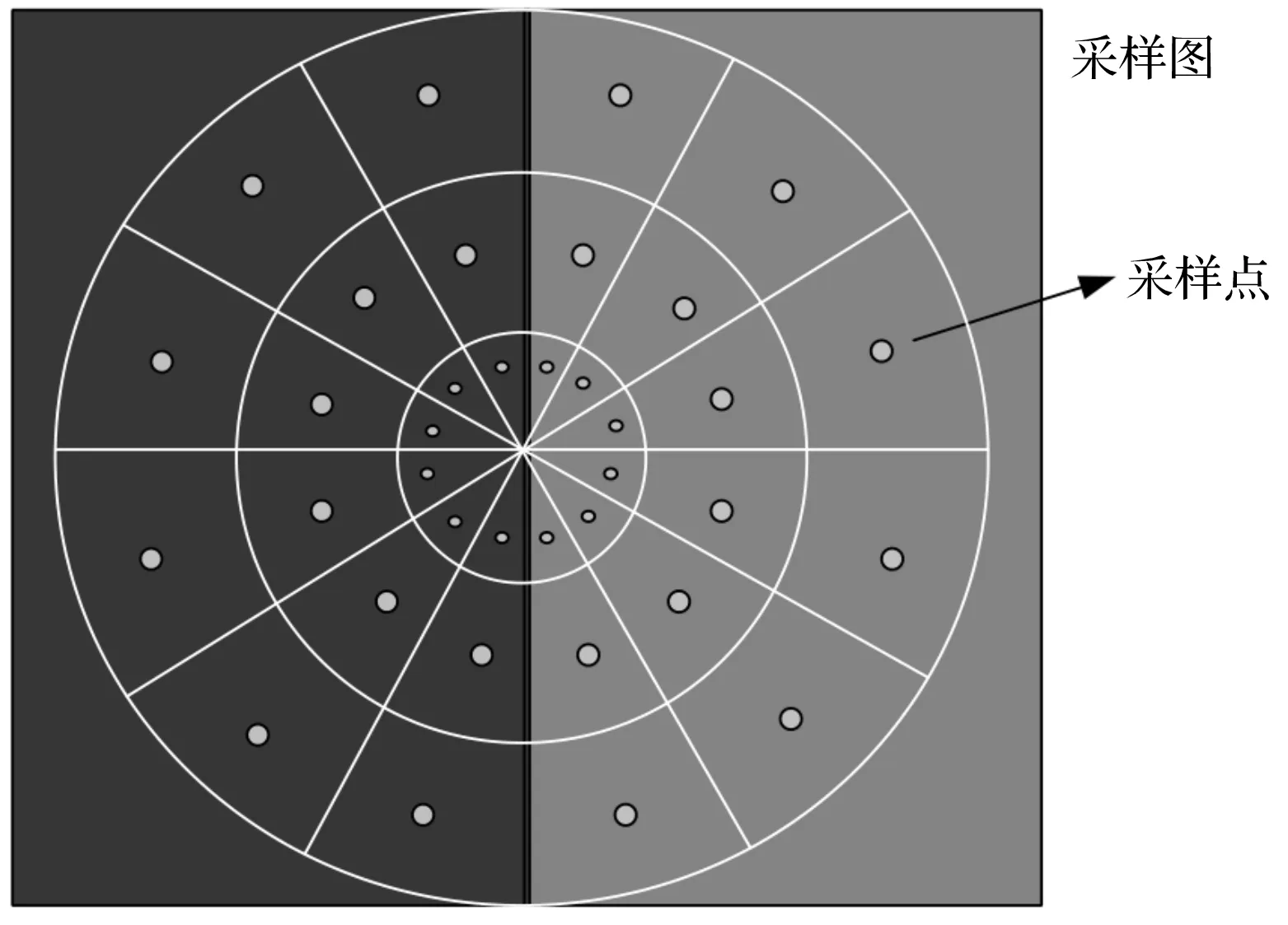
图7 采集方案

不同粗糙度等级表面对纹理方向的敏感度不同。粗糙度小的表面敏感度偏低;粗糙度大的表面敏感度偏高。

本文利用这种相关性,综合考虑混叠度和敏感度两种指标,评价磨削表面粗糙度,定义出度量指标Cusd,具体如下:

(2)

本文实验中采集了θ为0°、15°、30°、45°、60°、75°、90°时的图像,n=7。具体计算方法如下:

Step1:旋转角θ=0°;

Step2:采集图像,颜色空间转换RGB to Luv;

Step3:计算M个采样点的色彩均匀度Cu;

Step4:样块旋转15°;

Step5:θ>90°进入Step6,否则返回Step2;

Step6:基于各个角度的Cu计算Cusd。

3 数据获取

3.1 数据获取过程

笔者在磨床上加工20块50 mm×50 mm的#45钢块，采用TR-200型指针式粗糙度测量仪对样块进行测量,为了保证数据的准确性,测量时保证仪器的走针方向与样块打磨的纹理方向垂直,每个样块测量6次并取平均值。

20块样块的粗糙度测量值如表1所示。图像数据的获取流程如图8所示。拍摄时尽可能保证图像红绿区域对称。

表1 指针式粗糙度测量仪测量结果

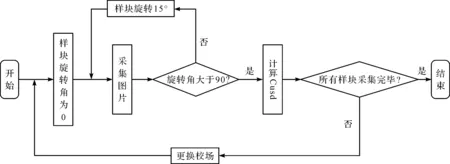
图8 反射图像数据获取过程

3.2 评价指标

选用斯皮尔曼系数ρ验证各种测量指标与粗糙度值之间的相关性。斯皮尔曼系数ρ为统计学中评价两个统计变量相关性的指标。当ρ>0时,两个变量呈正相关;当ρ<0时,两者呈负相关;|ρ|越大,变量之间相关性越强。

斯皮尔曼系数ρ如下式所示:

(3)

式中:N—实验样块个数;di—对变量X(粗糙度值)与Y(测量指标值)排序后对应秩次的差值。

4 实验及结果分析

为了说明本文提出的测量指标Cusd与粗糙度之间的强相关性,笔者选取3种常用指标进行对比实验,分别是灰度共生矩阵[8]578的相关参数:对比度Co、能量En和彩色图像重合度Scy[10]99(注:灰度共生矩阵以45°、偏移距离为1计算)。

4.1 相关性对比与分析

为了模拟磨削表面不同纹理方向,实验中将样块分别旋转0°到90°(间隔15°)。表1中20块粗糙度样块在不同旋转角度下En、Co和Scy3种度量指标和粗糙度的相关性系数ρ值，如表2所示。

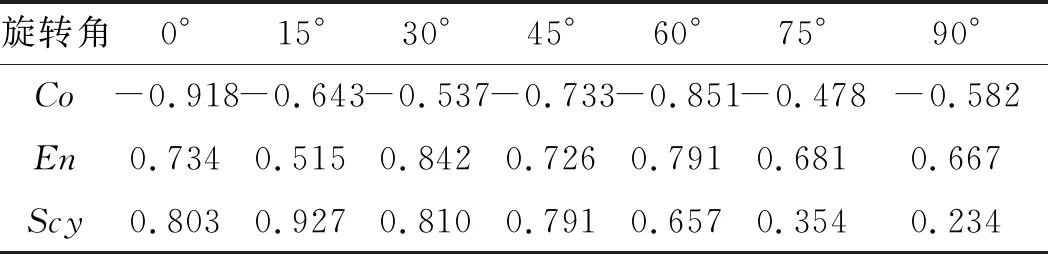
表2 各指标在不同旋转角下与粗糙度的相关性系数

从结果看,En、Co和Scy对纹理方向的敏感性比较高。其中,Co与Ra负相关,En、Scy与Ra正相关。当旋转角θ=0°时,Co与粗糙度Ra的相关性ρ最高,为-0.918;当旋转角θ=30°时,En与粗糙度Ra的相关性ρ最高,为0.842。

磨削表面在合适的旋转角下,灰度指标Co、En与粗糙度Ra有较强的相关性,但事实上Co、En与Ra的相关性ρ随旋转角θ的变化规律并不明显。所以,在实际操作中选择合适的旋转角比较困难。

Scy是彩色图像指标,θ=15°时Scy与Ra的相关性ρ最高,为0.927。随着旋转角θ增加,Scy与Ra的相关性ρ明显减少,出现这种情况和Scy与Cu类似描述红绿区域的重合度相关。根据1.2节分析可知:对于同一样块,当θ增大时,红绿颜色的混叠程度会增大;在θ较大时,即使是粗糙度很低表面的红绿混叠程度也较大,此时的θ是影响红绿混叠程度的主要因素。

本文提出的度量指标Cusd综合考虑不同旋转角θ时的色彩混叠情况,描述色彩混叠程度对不同纹理方向的敏感性。因此,Cusd不受旋转角θ的影响。

不同旋转角下Cusd的计算结果如表3所示。

色彩均匀度Cu描述了红绿光的混叠情况。由表3可知:对同一样块,随着旋转角的增加,Cu大致呈减少趋势,混叠效应增加。这也验证了前文的分析:纹理方向会对反射光混叠程度产生影响。另外,Cusd从上至下逐渐增加,说明粗糙度越大,对旋转角改变的敏感度越高,与前文的结论一致。Cusd与Ra的相关性系数ρ为0.978,为各个指标中最高,和粗糙度之间存在强相关性。

表3 不同旋转角下Cusd计算结果

4.2 粗糙度测量精度对比与分析

为了验证Cusd指标的粗糙度测量精度,笔者随机抽取了10个样本作为测试样本,其余样本作为标定样本,利用SVM对样本数据进行拟合以达到预测粗糙度的目的。

笔者使用各指标最优旋转角度下(即指标与粗糙度相关性最大时的旋转角)的数据进行粗糙度预测，各指标的粗糙度预测结果如表4所示。

灰度指标的预测均方差要明显大于两种彩色指标,说明虽然灰度指标与Ra相关系数较高,但灰度指标的预测能力较弱。另外,对于表4粗糙度区间为0.017 μm～0.646 μm的测试样本,可计算出Cusd的平均预测误差为0.02 μm且Cusd的预测均方差小于Scy,说明Cusd预测精度较高。

表4 各指标的粗糙度预测结果

各指标的预测误差图如图9所示,横轴是测试集按粗糙度由小到大排列的序号,纵轴是预测的粗糙度值。灰度指标Co和En的预测曲线波动性大、单调性差,与彩色指标相比预测误差较大。与Scy相比,Cusd预测曲线的上升曲线更平滑,说明Cusd与Ra的鲁棒性更好,也证明了本文测量方案和指标的可行性。

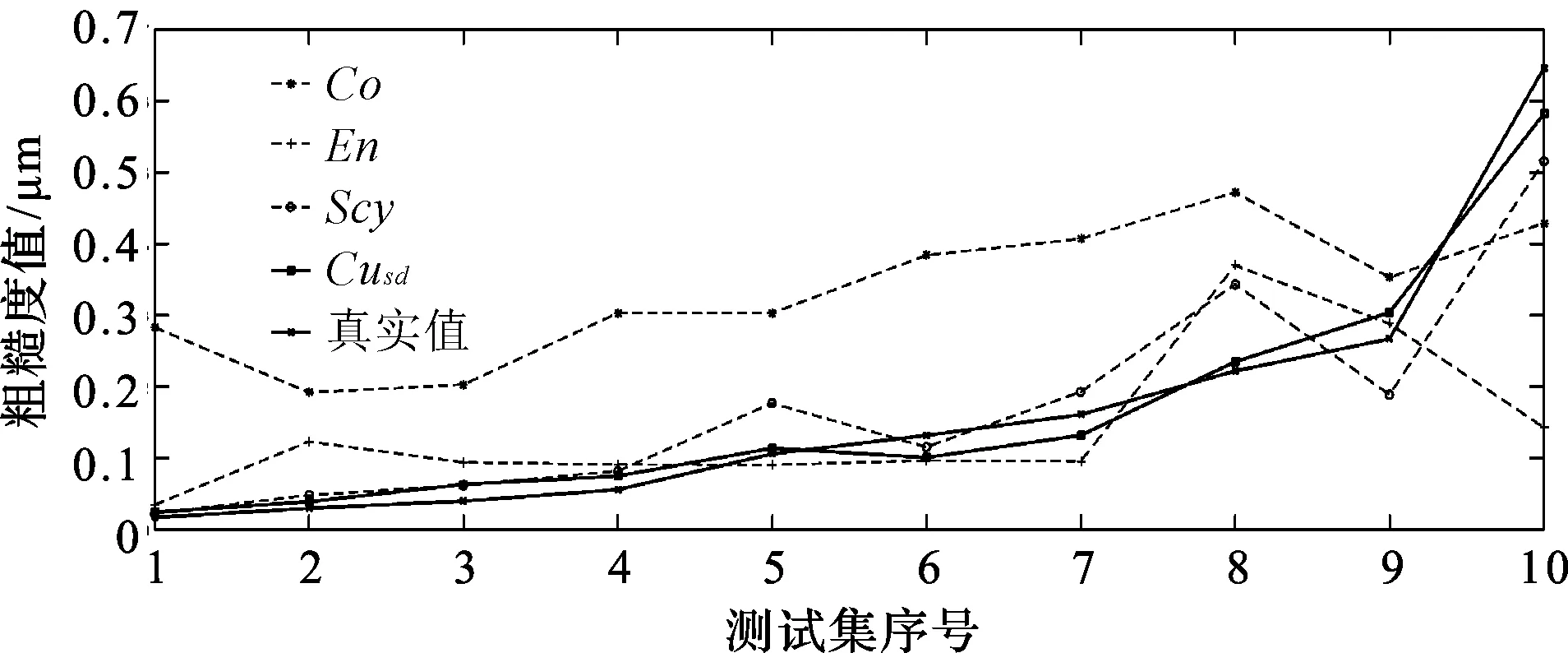
图9 彩色指标预测误差图

5 结束语

磨削加工表面粗糙度低、表面纹理弱,且有特定纹理方向。笔者针对磨削表面特点,设计了一个基于彩色光反射图像的磨削表面粗糙度测量方案,并分析了其粗糙度测量机理。结合磨削表面存在的纹理方向特性设计了一种色彩均匀敏感度指标Cusd,建立了反射图像与粗糙度的相关性,并基于搭建的测量平台实现了对磨削表面粗糙度的测量。

实验结果表明:相对于现有的3种指标,本文提出的Cusd测量指标能和粗糙度建立很强的相关性,斯皮尔曼相关性系数ρ达到0.978 9,且对表面纹理方向不敏感。对粗糙度Ra范围在0.017 μm～0.646 μm的磨削表面,平均测量误差为0.02 μm,具有良好的粗糙度预测能力,证明了本文方法的可行性。

由于本文方法数据获取较麻烦,且Cusd计算复杂等问题,进一步简化算法、提高计算效率是后续要开展的主要工作。