表面粗糙度比较样块全国大区级计量比对

杨 斌

(辽宁省计量科学研究院，沈阳 110004)



表面粗糙度比较样块全国大区级计量比对

杨 斌

(辽宁省计量科学研究院，沈阳 110004)

由东北国家计量测试中心组织，辽宁省计量科学研究院作为主导实验室进行表面粗糙度比较样块全国大区级计量比对工作。文章介绍了比对方法、比对数据和结果分析。针对此次比对工作过程中出现的问题，着重讨论了表面粗糙度比较样块传递标准稳定性，并且分析了样块不均匀引入的标准不确定度分量对测量结果扩展不确定度的影响，为以后此类计量器具计量比对提供了重要的参考价值。

计量学；表面粗糙度比较样块；比对；传递标准稳定性；不确定度

0 引言

表面粗糙度比较样块[1]是用来检查制件表面粗糙度的一种工作量具，它是以样块工作面的表面粗糙度为标准，凭触觉(如指甲)、视觉(可借助于放大镜、比较显微镜)与被检制件表面进行比较，从而判断制件表面粗糙度是否符合要求。由国家东北计量测试中心组织，辽宁省计量科学研究院作为主导实验室进行表面粗糙度比较样块全国大区级计量比对工作。此次比对反映了目前我国各大区级计量技术机构表面粗糙度比较样块的校准能力和量值的准确一致性。

1 比对样品和测量方法

本次比对共6个大区级实验室参加，分别为东北、华南、中南、华北、西南、华东大区级计量院。传递标准采用6块表面粗糙度比较样块，由于表面粗糙度比较样块测量时易磨损，因此采用3套标准进行“花瓣式”传递[1]，编号分别为Ⅰ、Ⅱ、Ⅲ。该方式由若干个小环式组成，在进行几个参比实验室的比对后，将传递标准返回主导实验室进行复校，优点是可以将无效比对控制在比对过程的某一环节。依据JJF 1099—2003表面粗糙度比较样块校准规范[2]，对每块样块在垂直于纹理加工方向上进行10次测量，并求其平均值Ra对其标称值的偏差。见表1。

表1 传递标准

2 比对结果

经核查和确认，各参比实验室提供的数据见表2。其中参考值由主导实验室提供。

表2-Ⅰ 比对结果

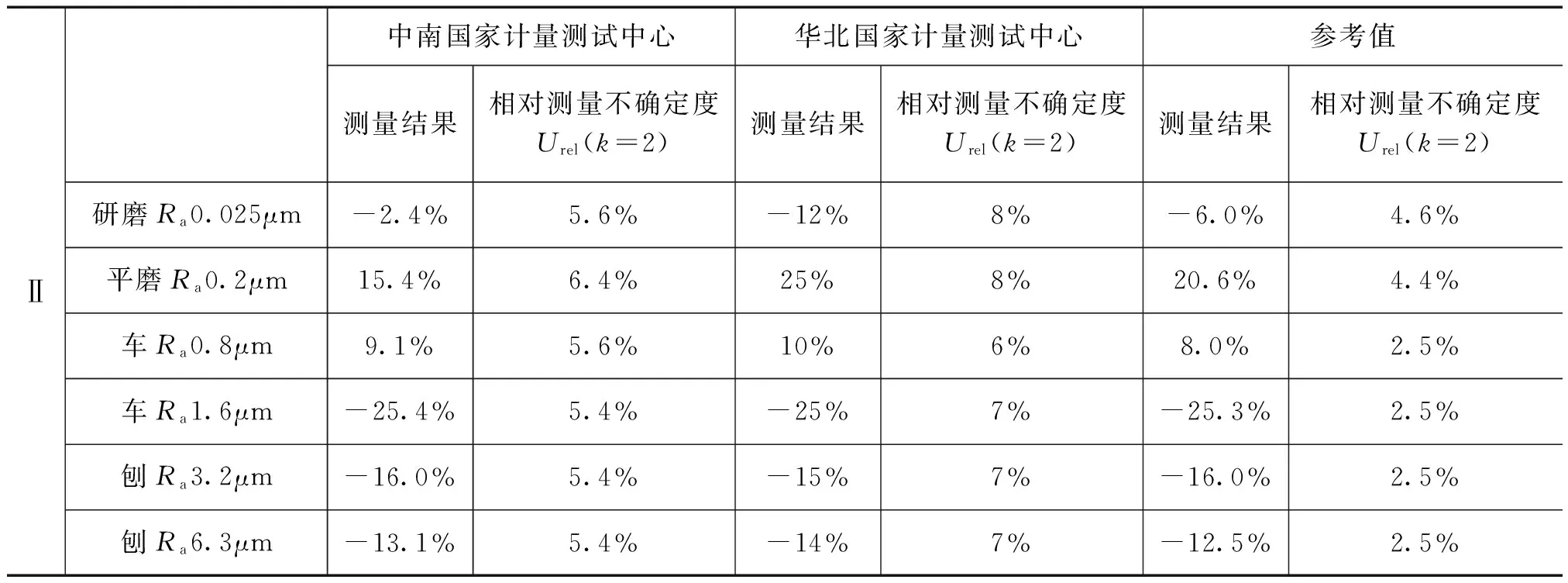
表2-Ⅱ 比对结果

表2-Ⅲ 比对结果

3 结果分析

依据JJF 1117—2010《计量比对》，用归一化偏差En值来评价每一个实验室所给出的测量结果[3]。

(1)

式中：Yji为第j个实验室上报的在第i个测量点上的测量结果；Yri为主导实验室在第i个测量点上的测量结果；k为覆盖因子，一般情况k=2；ui为第i个测量点上Yji-Yri的标准不确定度；当uri，uei与uji相互无关或相关较弱时，

(2)

式中：uri为第i个测量点上参考值的标准不确定度；uji为第j个实验室在第i个测量点上测量结果的标准不确定度；uei为传递标准在第i个测量点上在比对期间的不稳定性对测量结果的影响。当En值为|En|≤1，判定为满意；|En|>1判定为不满意。

表面粗糙度比较样块计量比对En值统计见表3。

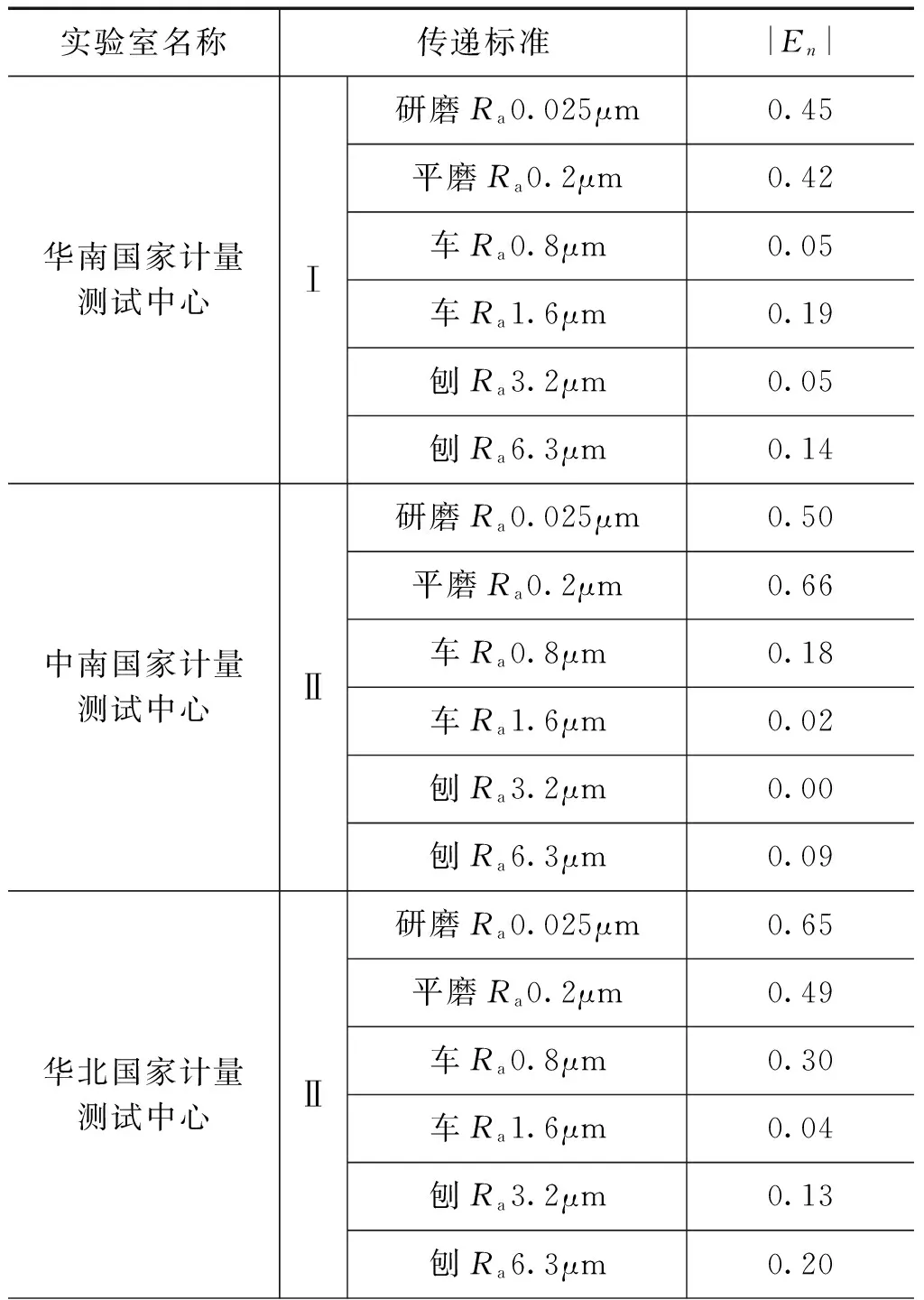
表3 En值统计表

续表

4 传递标准稳定性

计量比对中，必须保证传递标准的稳定性[4]。如果标准器不稳定，则带来测量不确定度偏大，降低了比对的效果。由主导实验室在比对前后对三套传递标准分别测量，每隔一个月进行一次测量，共进行4次测量[5]，三套传递标准(编号分别为Ⅰ、Ⅱ、Ⅲ)的稳定性用标准偏差来表示，见式(3)。测量结果见图1～图3，分析见表4。

(3)

图1 样块Ⅰ稳定性

图2 样块Ⅱ稳定性

图3 样块Ⅲ稳定性

表4 稳定性分析

u≤uc

(4)

uc为表面粗糙度比较样块测量结果的合成标准不确定度。

从表4中可以看出，三套传递标准u

5 不确定度分析中的问题

从比对结果中可以看出，除了华东大区级计量院以外，其余大区级计量院对于“车和刨”样块给出的不确定度[6]都接近主导实验室的2倍。在不确定度分析中，主要是仪器重复性、仪器示值误差以及表面粗糙度样块的不均匀等3个来源，而各参比实验室使用的仪器示值误差基本在2%～5%之间，与主导实验室仪器示值误差2%相差不大，但是还能出现接近2倍的扩展不确定度。通过结果分析发现，这是因为大多数实验室在评价表面粗糙度样块的不均匀性时直接使用了规范中规定的“Ra分散性用标准偏差评定，实验标准偏差不得超过4%”，即取上限值4%来计算，而没有具体对每一块表面粗糙度比较样块做10次测量的分散性实验标准偏差计算。实际上由于比对采用的表面粗糙度比较样块质量很好，表面很均匀，因此实际计算值相比取上限值4%来说很小。见表5(样块Ⅰ)所示。

从表5中可以看出，对于车和刨样块，由样块不均匀引入的标准不确定度按上述两种计算方法差值最大的可以达到10倍多，除了研磨和平磨样块外，其余也在6倍左右。因此这也大大地增大了测量结果的扩展不确定度。

表5 样块不均匀引入的不确定度两种计算方法结果分析对比

6 结论

文章阐述了表面粗糙度比较样块全国大区比对的比对方法、比对数据，结果满意。对表面粗糙度比较样块传递标准稳定性进行了探讨并分析了测量结果的不确定度中由表面粗糙度比较样块的不均匀性引入的标准不确定度两种计算方法对测量结果的影响。由于相关文献未见类似表面粗糙度样块比对文章，因此此文也为以后类似比对工作提供了重要的参考价值。

[1] JJF 1117—2010，计量比对[S]

[2] JJF 1099—2003，表面粗糙度比较样块[S]

[3] 李庆中.两种计量比对[J].计量技术，2006(3)：42-43

[4] 赵万星等.量值比对中传递标准稳定性评估及作用[J].工业计量，2013，23(4)：9-13

[5] 张海燕，黄健.干涉显微镜标准装置表面粗糙度量值传递的不确定度[A].第三届第五次全国气动实验测控自动化技术交流会论文集[C]，1998

[6] 倪育才.几何量测量不确定度评定[M].北京：中国计量出版社，2006：58-135

10.3969/j.issn.1000-0771.2015.09.15