基于灰色理论的亳州地区房地产价格预测研究

闫 磊，张钰彪，赵志浩

(亳州职业技术学院 信息工程系,安徽 亳州 236800)

0 前 言

房地产一向是人们安身立命的基本需求以及投资保值的最佳选择。长期以来国内房地产市场的价格信息并不透明，常因房地产开放商为了争取最大利益和炒房者大量购买等情况造成房地产价格的不合理上涨，普通购房者购房压力日益加重，严重影响到人们的生活质量。为了缓和房地产价格的波动以及促进相关市场经济的合理发展，中国现已经开始出台和实施不动产制度和开发商授权价格制度，人们通过网络可以随时搜索到相关房地产价格信息与统计数据。而这些公开的信息与数据仍需经过进一步的分析与评价，才能产生有用的信息，来有效掌握相关房地产价格的趋势发展，为真正的购房需求者合理计划购房提供参考。

灰色理论GM(1,1)预测应用范围较广。在灾害预警、药品价格预测、故障诊断、农产品价格、物流运输等行业得到了广泛的应用，而且需要的样本数据较少，尤其是对价格预测准确度较高，可以直观的体现价格趋势变化。目前，亳州房地产市场发展较好。为了能够更好地对亳州房地产市场进行监督和管理，本研究以灰色理论GM(1,1)预测模型,根据不动产交易信息平台的购房交易的统计数据，分析亳州三县一区的房地产价格，预测未来亳州三县一区房地产交易价格的年度及季度价格的发展趋势。

1 灰色理论的发展

1.1 灰色理论概述

灰色理论(grey theory)是Deng于1982年提出。主要研究少量数据不确定性理论，信息完全确定者为白色系统，信息完全缺乏者为黑色系统，信息不完全、不确定者为灰色系统(grey system)，对系统信息不确定、信息不完整的灰色系统，可使用灰色理论进行研究分析[1]。一般传统统计分析是利用概率及统计理论来求得过程的规律性，所收集的数据越多，越能显示出该随机过程的相关特性，因此需要大量的数据来建构较为精确的系统模型[2]。而灰色理论在理论上则异于传统的随机过程处理方法，从而可使用于信息不明或不完全的灰色系统[3]。其处理要点在于不将系统中的随机性看成一个随机信号，而是将它看成一个灰数，将随机量当作一定区间变化的灰色量，将灰色过程当作在一定范围、一定时间内变化的随机过程。灰色系统理论中灰色建模是利用生成的数据建立一组灰差分方程与灰拟微分方程的模式，称为GM模式[4]。GM模式一般可以分成下列几种模型：

(1)GM(1,1)：表示一阶微分，输入变量为一个，一般做预测用。

(2)GM(1,N)：表示一阶微分，输入变量则为N个，一般做多变量关联分析用。

(3)GM(0,N)：这是GM(1,N)的特例，表示零阶微分，而输入变量则为N个，一般做多变量关联分析用。

1.2 灰色预测

本研究应用的灰色预测是以GM(1,1)模型为基础，对现有数据所进行的预测方法，主要优点在于所需的数据少以及数学基础简单[5]。在传统预测中，一般都是使用连续函数拟合的方法做外插预测，基本上可以分成短间隔、中间隔及长间隔三大类[6]；另外拉格兰日内插法则是用在非等间距的内插预测上，这些方法有些是限制在等间距上，有些是在非等间距的预测上精度较低，虽然使用上较方便但却需要大量的已知数据否则会产生无法预测的情形[7]。而灰色预测则无此缺点，只要利用已知4个数据点即可以做预测，除了采取逐点方式预测及准确度较高以外，在非等间距的预测上也具有相当高的准确度[8]。

2 灰色模型在亳州房地产价格预测中的应用

查询亳州不动产信息平台的商住房统计信息，取得2017-2019年亳州三县一区普通商住房交易价格平均单价的时间序列数据，见表1。

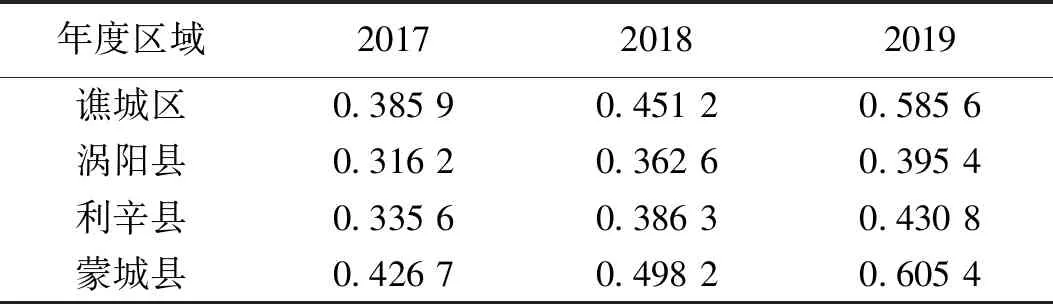
表1 亳州地区2017-2019年商住房交易平均单价 万元·m-2

灰色GM(1,1)基本模型分析如下：

GM(1,1)模型的定义：由灰色系统理论定义，GM(1,1)模型的灰微分方程为公式(1)所示。

(1)

其中，a、b为系数，以及

(2)

经由逆累加运算，可以得到公式(3)

x(1)(k+1)-x(1)(k)=x(0)(k+1)

(3)

再由背景值x(1)的定义可以得到公式(4)

x(1)(k)→0.5x(1)(k)+0.5x(1)(k-1)=z(1)(k)

(4)

通过公式(4)可以到得到GM(1，1)模型的灰差分方程式，如公式(5)所示。

x(0)(k)+az(1)(k)=b

(5)

3 实验分析与结果

3.1 利用GM(1，1)模型对数据进行分析

根据表1所整理得的2017-2019年各年度的亳州地区(谯城区、涡阳县、利辛县、蒙城县)商品住宅价格的平均单价数据，以GM(1,1)预测分析模型执行相关统计分析，并对未来两年的亳州地区商住房的平均价格进行预测，预测分析步骤如下。

1)建立原始序列

x(0)=(x(0)(1),x(0)(2),x(0)(3),…,x(0)(k))

(6)

2)AGO(accumulated generating operation)累加生成

(7)

3)均值生成

z(1)=(- - -,z(1)(2),z(1)(3),…,z(1)(k))

z(1)(k)=ax(1)(k-1)+ax(1)(k+1)

其中，z(1)(k)为生成数，k=2,3,4,…,n。a为生成系数并且a∈[0,1]，当a=0.5时为均值生成。x(k-1)为前邻值，x(k+1)为后邻值。

4)建构Y矩阵及建构B矩阵

5)解出模型参数a和b

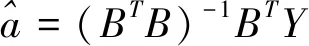
6)建构灰色预测方程式，于公式(8)中代入所求出的a和b的参数值。

(8)

7)计算出各预测数值

依次将k=1,2,3,…,n代入上述已构建的灰色预测方程式，求出各预测值。

8)根据公式(9)计算各预测值与真实值之间的相对误差。

(9)

9)计算平均值绝对值误差百分比

(10)

根据步骤7)、8)、9)，分别可以得出预测值与真实值的相对误差和平均值绝对误差，从而对数据进行分析。

3.2 预测结果

通过GM(1,1)预测分析模型得到谯城区、涡阳县、利辛县和蒙城县的年度商品住宅价格的预测结果，见表2。谯城区2018及2019年度的商住房交易价格平均单价分别为每平方米0.451 2万元及0.585 6万元，年度涨幅各约在16.92%及29.79%，预测未来两年商品住房平均价格各约为每平方米0.652 3万元及0.702 5万元，年度预测涨幅各约为10.09%及7.70%；涡阳县2018及2019年度的商住房交易价格平均单价分别为每平方米0.362 6万元及0.395 4万元，年度涨幅各约为14.67%及9.05%，预测未来两年商品住房平均价格各约为每平方米0.358 7万元及0.395 0万元，年度预测涨幅各约为18.58%及10.12%；利辛县2018及2019年度的商住房交易价格平均单价分别为每平方米0.386 3万元及0.430 8万元，年度涨幅各约为15.11%及11.52%，预测未来两年商品住房平均价格各约每平方米0.520 6万元及0.589 0万元，年度预测涨幅各约为11.55%及18.16%；蒙城县2018及2019年度的商住房交易价格平均单价分别为每平方米0.498 2万元及0.605 4万元，年度涨幅各约为16.76%及21.52%，预测未来两年商品住房平均价格各约每平方米0.632 5万元及0.686 3万元，年度预测涨幅各约为17.58%及19.59%。

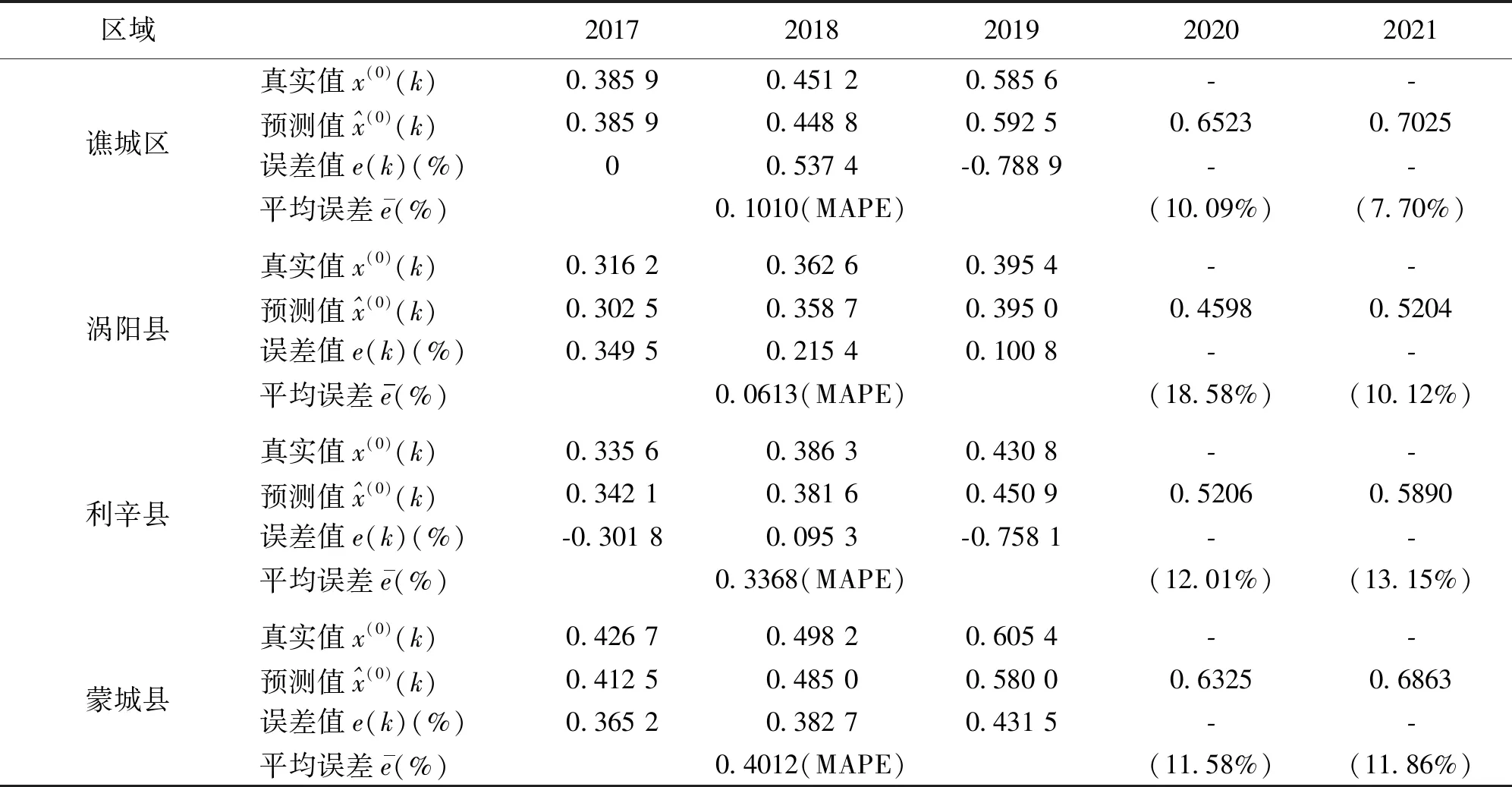
表2 2017-2021年亳州地区年度价格预测结果 万元·m-2

表3为MAPE预测能力分级，主要分为良好的预测、好的预测、合理的预测和不正确的预测4个等级。

表3 MAPE预测能力等级

通过上面数据与等级预测表匹配，均小于20%，为好的预测能力等级，说明预测具有良好的预测精准度。因此本研究成果显示灰色理论GM(1,1)预测模型具有相当可靠度的预测性能。

4 结 论

本研究利用灰色理论GM(1,1)预测模型具有运用数据量少以及数学基础简单的特性。通过GM(1,1)对亳州地区三县一区房地产价格进行预测，以年度平均商住房交易价格的平均单价预测值与真实值相比较，分析结果得出相关误差值皆属于优良预测水平，预测精准度高。显示灰色理论GM(1,1)预测模型具有很好的预测能力。灰色理论GM(1,1)预测模型为亳州地区房地产行业管理部门对商品房价格的监督和管理提供了技术支持，同时也为购房者提供了参考依据。