组合预测模型在红卫农场年降水量预测中的应用

李 娜，孙颖娜，王 烨，杜 崇

(黑龙江大学 水利电力学院，哈尔滨 150080)

0 引 言

三江平原是我国重要的商品粮生产基地，降水量的多少直接影响着农业的灌溉和发展，许多学者致力于精确地降水量预测研究。陈沪生等[1]应用小波与 ARIMA组合模型对黄山市年降水量进行预测，发现小波与 ARIMA组合模型预测结果较好。仲远见等[2]和沈永梅等[3]改进了马尔可夫链预测模型并应用到实例中，预测结果与实测资料相吻合。ARIMA-Markov组合预测模型是在ARIMA模型预测降水量的基础上，借助马尔可夫链缩小预测区间，提高降水量预测精度。模型在给出降水量预测值的同时，能够提供降水量预测区间、状态转移概率、误差波动幅度及波动趋势等信息，该方法对水文序列长度要求不高，方法更加简单有效[4-7]。本文利用三江平原红卫农场1967—2009年年降水量数据，建立基于自回归滑动平均模型与马尔可夫链的组合预测模型(ARIMA-Markov组合预测模型)，对红卫农场2009—2019年年降水量进行模拟预测。

1 研究区概况

红卫农场是黑龙江省的一处国营农场，隶属于建三江农场管理局。农场位于三江平原东北部的完达山北麓、挠力河畔，南、北低洼，沼泽较多，中间平坦且土壤肥沃。气候属寒带大陆季风气候，平均年有效积温2 300～2 400 ℃，平均年降水量550 mm，无霜期为130 d左右，适宜作物生长，具有生产优质水稻独特优势。

红卫农场总播种面积39 666.67 hm2，粮食总产36.83×104t。曾多次获得“全国粮食生产先进场”称号，并被农业部授予“水稻标准化生产示范场”称号[8]。多年来，红卫农场凭借良好的生态环境和科学化种植，奠定了绿色产业的雄厚基础。

2 ARIMA-Markov组合模型的构建

2.1 ARIMA预测模型

ARIMA模型是将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。模型被识别后从时间序列的过去值及现在值来预测未来值。该模型将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归。ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)以及ARIMA过程。ARIMA 模型适合预测线性、稳定的时间序列，能够有效去除序列的趋势成分，使数据的随机过程平稳化。

ARIMA模型较为简单，模型不需要借助其他外生变量，要求时间序列数据是稳定的，或者是通过差分化后是稳定的，只能预测线性关系，不能预测非线性关系。方法简单易操作，但预测精度一般。

2.2 Markov预测模型

马尔可夫链是对系统状态用随机变量表示的一种随机过程。每一个阶段的系统状态都对应一定的概率(状态概率)，若系统某一阶段状态发生改变，就存在状态转移概率[9]。状态转移概率只与目前系统所处状态有关，与之前状态无关，具有这种离散状态的随机系统转移过程被称为马尔可夫过程[10-11]。

马尔可夫过程是马尔可夫链预测的理论基础。分析马尔可夫过程的变化，主要研究链内有限随机过程的状态及各个状态之间的相互关系，再对链的未来状况进行预测。Markov模型为

x(n)=x(0)Pn

(1)

式中：x(0)和x(n)分别为初始时刻和n时刻的状态概率向量；P为状态转移概率矩阵。

状态转移概率指在事件的发展变化过程中，如果某一时刻的所在状态为起点，那么未来某时刻发展为其它状态的可能性。由状态Ei转为状态Ej的状态转移概率P(Ei→Ej)，表达式为

P(Ei→Ej)=P(Ej/Ei)=Pij

(2)

状态转移概率矩阵：设某事件有n个发展状态，即E1，E2，…，En。若由Ei转变为Ej的状态转移概率记作P(Ei→Ej)，那么矩阵

(3)

称为状态转移概率矩阵。

Markov预测模型需要通过状态划分确定系统存在的状态，然后计算相应的状态转移概率矩阵，得出预测区间[12]。

Markov预测模型优点为一个系统由一个状态转至另一个状态的转换过程中，存在着转移概率，并且这种转移概率可以依据其紧接的前一种状态推算出来，与该系统的原始状态和此次转移前的马尔可夫过程无关。缺点在于，理论上只能用于预测短期内的数据，而不适合用于系统中长期数据的预测。

2.3 ARIMA-Markov组合预测模型

基于对以上2种模型的分析，将ARIMA模型与马尔可夫模型有效结合，充分发挥2种模型优点，建立ARIMA-Markov组合预测模型，对年降水量进行预测，依据相对误差，判定组合模型的精确度。

ARIMA-Markov组合预测模型建立的基本步骤：①建立ARIMA模型，计算相对误差;②根据归一化相对误差序列划分状态区间，反归一化处理得出Markov状态区间(采用1∶0.618比例的黄金分割率法，计算系统存在的状态区间[13-14]);③确定已有年份降水量数据所处的状态，应用Markov模型确定状态转移概率矩阵;④根据预测值在不同区间的概率确定预测值的取值范围;⑤根据确定的取值范围，取区间均值作为最后预测结果。

ARIMA-Markov组合预测模型的优点在于：应用Markov模型对ARIMA模型预测的结果进行状态区间划分，根据状态区间的状态转移概率得出最优年降水量区间，取区间均值作为最终预测结果。它不同于应用ARIMA模型、Markov模型分别预测年降水量，取2种方法预测结果的均值作为最终预测结果的方法。

3 ARIMA-Markov模型在红卫农场年降水量预测中的应用

3.1 基础数据处理

以红卫农场1967—2009年年降水量数据率定模型参数，2010—2019年年降水量数据进行模型检验。为使年降水量时间序列平稳化，对其进行一阶差分处理，经过多次试验，ARIMA(2，1，10)预测效果最佳，相关系数R2=0.388，相关系数偏低，故考虑二阶差分处理。通过判断ACF和偏ACF的拖尾性、截尾性进行参数评估，最终选取ARIMA(p，2，q)为ARIMA(0，2，1)模型最为合适[15-16]。

依据ARIMA(0，2，1)模型对红卫农场1967—2009年年降水量数据进行拟合，预测2010—2019年年降水量，划分年降水量状态区间，并对相对误差序列进行归一化处理[17-18]，预测检验结果与归一化处理结果见表1。由表1可见，ARIMA模型预测年降水量均位于置信区间内，且与真实值差异较小，相对误差最大为3.50%，最小为1.74%，平均为2.87%。计算出归一化相对误差均值为0.391 5，由此划分[0，0.226 5]， ( 0.226 5，0.618 0)和 [0.618 0，1] 3个状态区间。反归一化将各区间还原，其对应区间分别为[-0.035 0， -0.031 0]， (-0.031 0，-0.024 1)，[-0.024 1，-0.017 4]。

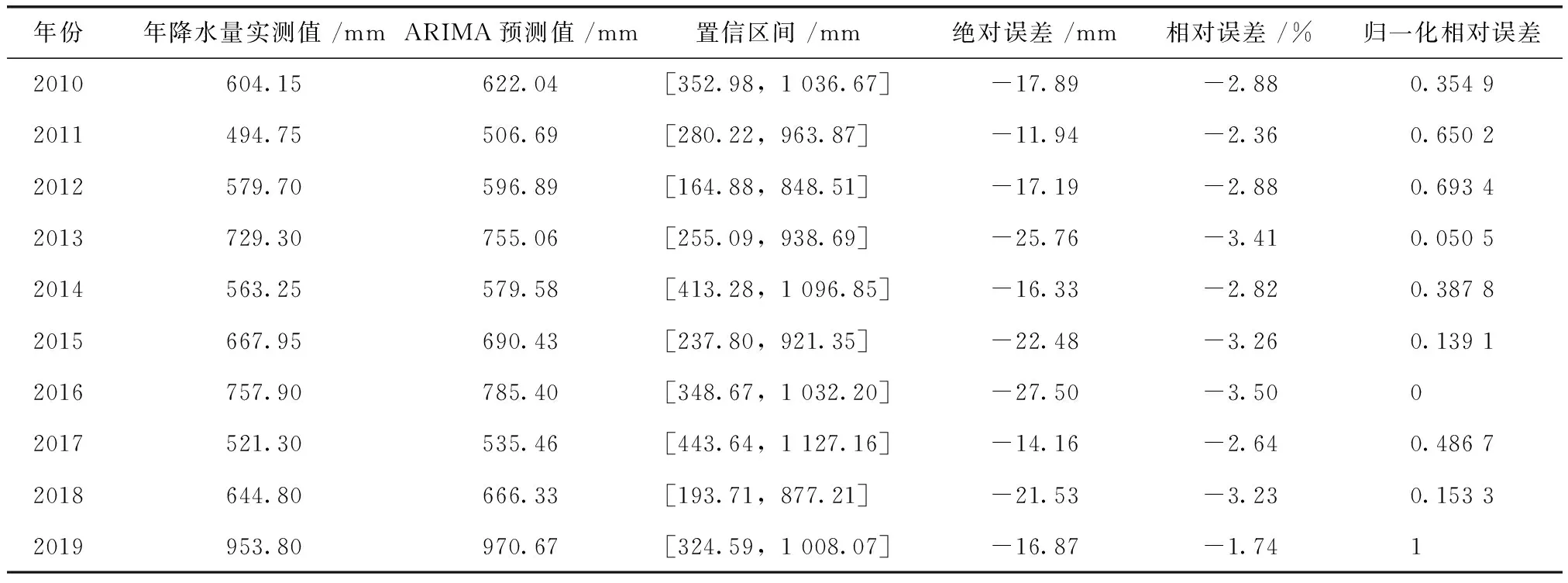
表1 ARIMA模型预测结果与误差归一化处理

根据划分好的区间，确定对应年份所处的状态，求得状态转移概率矩阵(步长为1)为[19-20]

(4)

3.2 组合模型应用

设q为原状态区间的分界值，X(0)(t)为还原后的区间分界值，Q(0)(t)为预测值[21]。则

(5)

可以得到

(6)

根据式(6)计算2010—2019年年降水量，结果见表2。

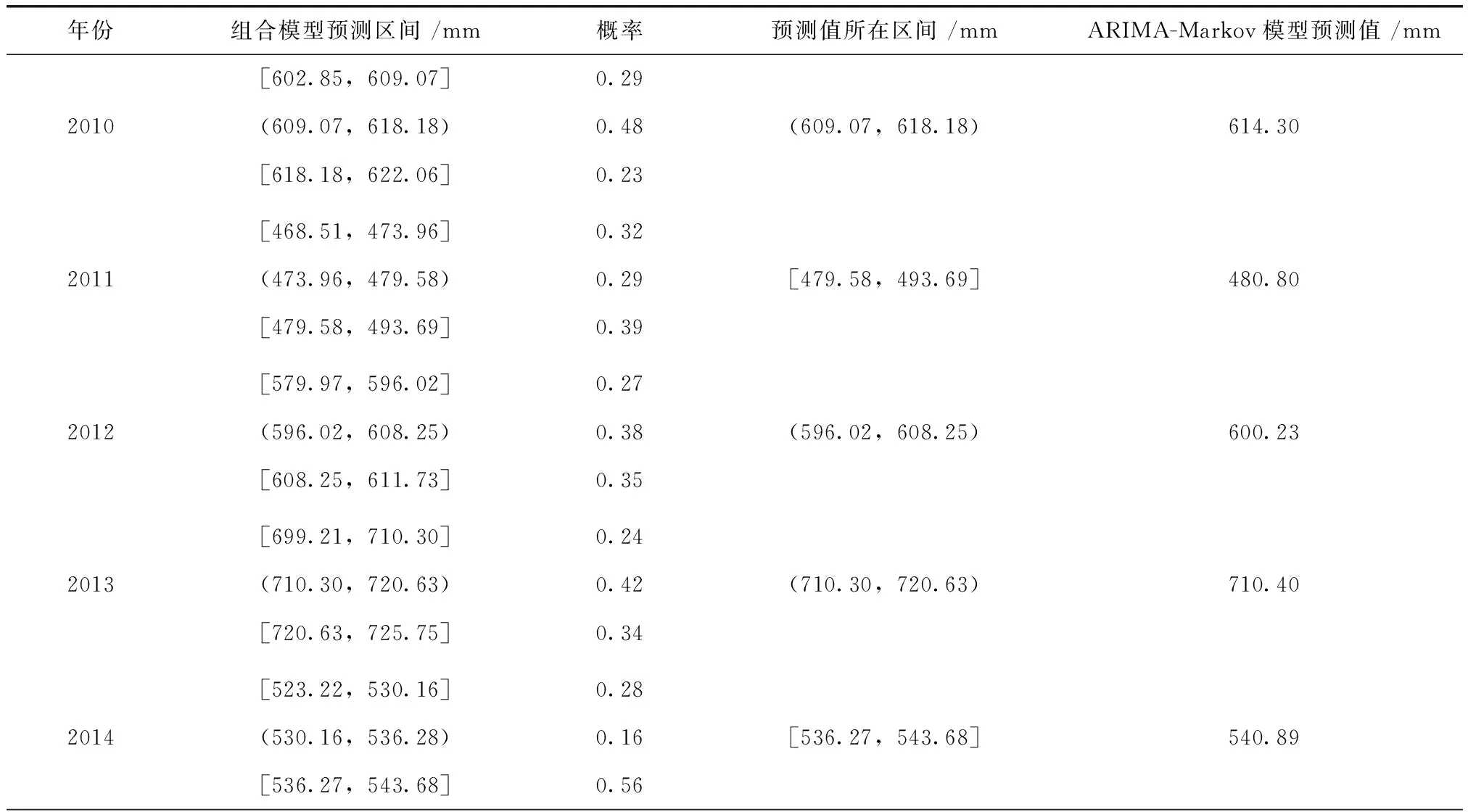
表2 2010—2019年ARIMA-Markov模型预测结果

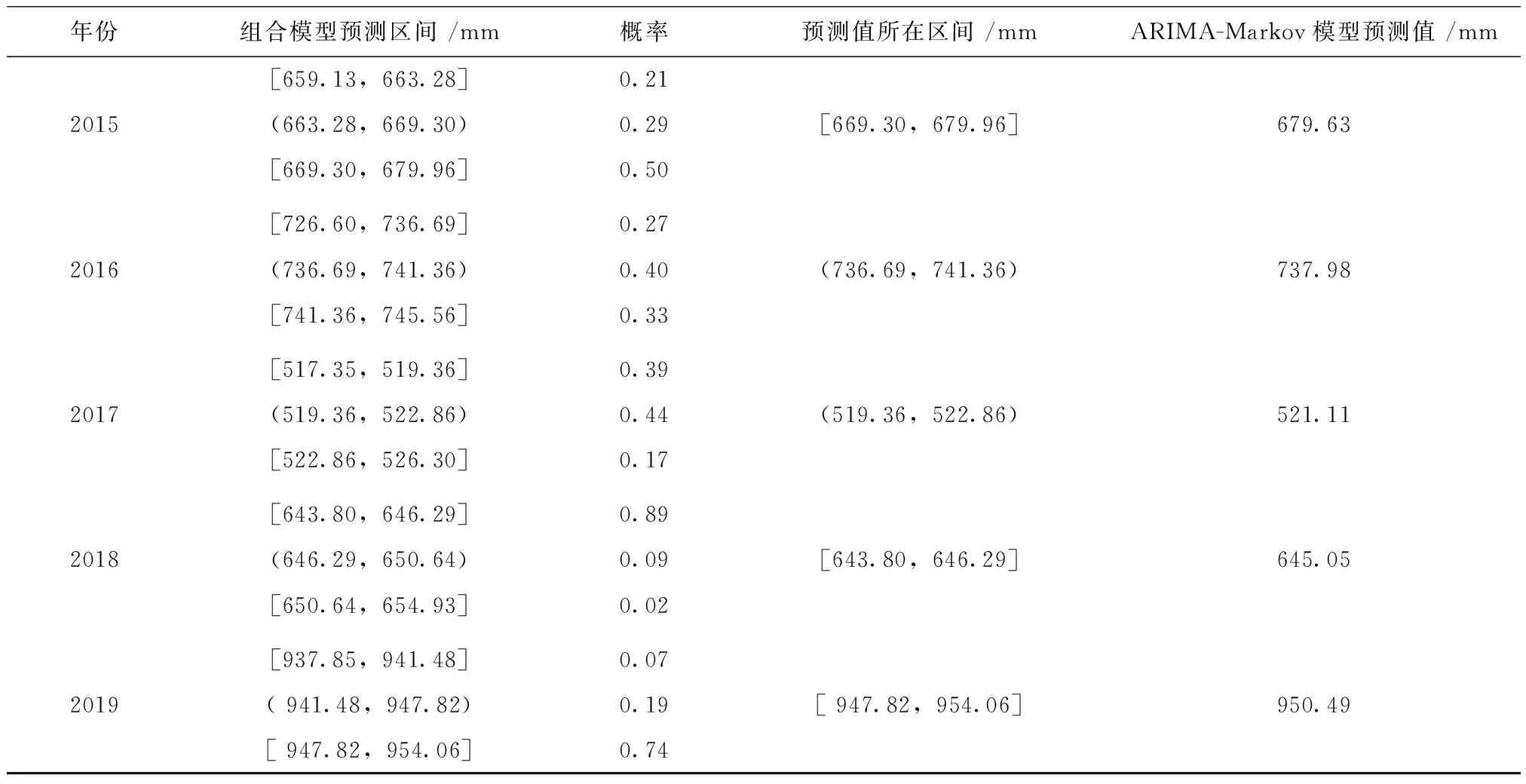
续表2

ARIMA模型与ARIMA-Markov模型预测结果精度见表3。由表3可见，ARIMA-Markov组合模型预测的相对误差明显低于ARIMA模型。依据ARIMA-Markov组合模型对红卫农场2010—2019年年降水量预测，其预测值均以最大概率落在对应的预测区间内，相对误差最大为3.42%，平均为1.34%。说明该模型应用于红卫农场年降水量预测可行且有效。

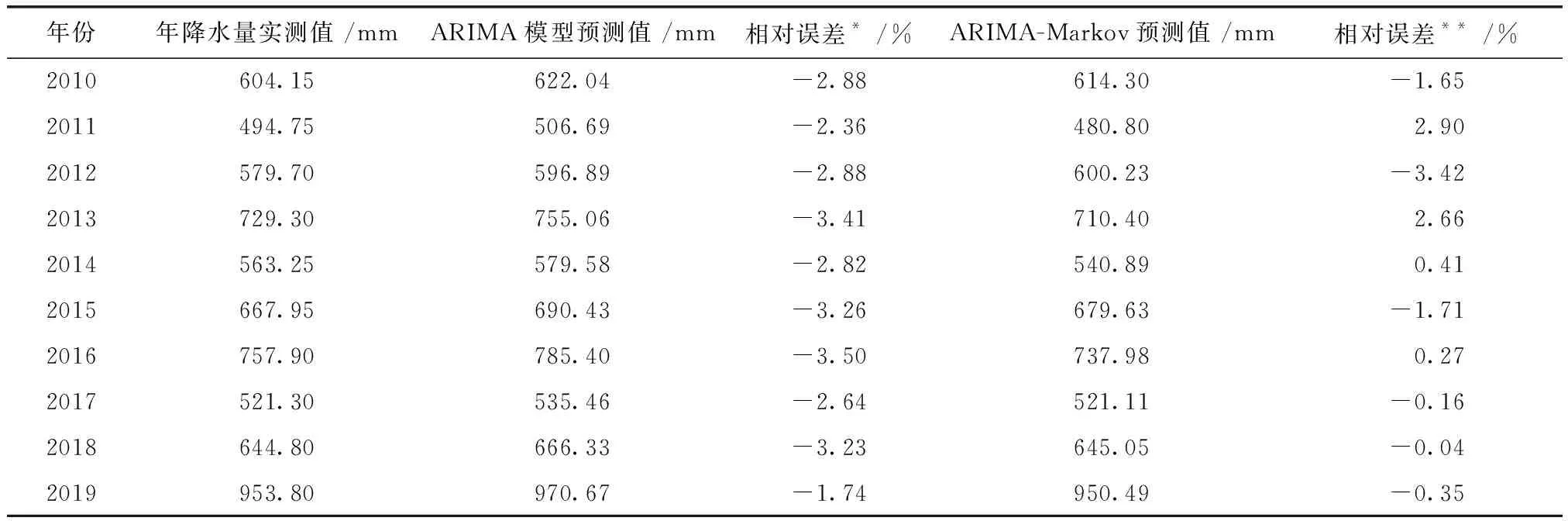
表3 ARIMA模型与ARIMA-Markov模型预测结果比较

4 结 论

以三江平原红卫农场43 a的年降水量资料，构建了ARIMA-Markov组合模型，并对红卫农场 2010—2019年年降水量进行了预测。结果表明：ARIMA-Markov组合模型预测的最大相对误差为3.42%，平均相对误差为1.34%，预报精度令人满意。组合模型在数据有限的情况下，简便易操作，该组合模型不但能精确地预测年降水量，并能给出年降水量预测区间和其概率，其结果可为农业生产及水资源规划等决策工作提供科学的依据。