基于范数比的LWT域自适应音频水印算法*

姚明明，杜庆治

（昆明理工大学，云南 昆明 650500）

0 引言

近年来多媒体技术不断进步，使得各种音频数字产品的传播变得越来越便捷，随之出现了一些负面影响，如盗版、侵权现象。因此，数字音频的使用和传输面临许多挑战，如安全、隐私和所有权等问题[1]。知识产权保护是数字音频中尚未解决的主要问题之一，而数字音频水印技术是解决这一问题行之有效的方法。数字音频水印是在音频信号中嵌入认证信息，以证明其所有权或版权的技术[2]。一个有效的数字音频水印方案必须满足鲁棒性、不可感知性和水印容量3个条件[3]。这3个条件相互制约，在实际的应用场景需要进行折中，如增加水印的嵌入容量就会使音频的质量下降。

数字音频水印算法主要包括时域和变换域。时域音频水印算法是直接在音频信号的采样点嵌入水印的方法，简单且嵌入容量高，具有代表性的算法有回声隐藏算法和最低比特位算法等。早期的音频水印算法是在时域内展开的，经过实验验证发现，其在抵抗音频信号攻击时表现的鲁棒性不佳。后来关于音频水印的算法主要集中在变换域上，变换域音频水印算法比时域音频水印算法有更好的鲁棒性和不可感知性[4]。常见的变换域包括离散傅里叶变换（Discrete Fourier Transform，DFT）[5]、离散余弦变换（Discrete Cosine Transform，DCT）[6]、离散小波变换（Discrete Wavelet Transform，DWT）[7]、奇异值分解（Singular Value Decomposition，SVD）[8]和范数[9]等。文献[10]提出一种基于LWT-SVD 的音频水印算法，对信号进行提升小波变换（Lifting Wavelet Transform，LWT）分解后，直接选取低频分量进行一维SVD 运算，然后通过量化非零奇异值嵌入水印。文献[11]提出了一种基于DWT-SVD 的大容量音频算法，把进行DWT 分解后的低频系数构造成一个矩阵进行SVD，然后把水印信息嵌入到奇异值矩阵的非对角线元素上，使得水印的嵌入容量得到提高。文献[12]提出了一种基于LWT 的音频水印算法，但鲁棒性不佳。文献[13]通过量化索引调制和SVD 将水印嵌入到二维矩阵的F-范数中。尽管这种算法有较好的不可感知性和较大的嵌入容量，但是其抵抗添加高斯白噪声和低通滤波攻击的鲁棒性表现不好，且矩阵范数的计算复杂度较大。相比之下，向量范数的计算复杂度较低。

为此，本文提出一种基于范数比的LWT 域自适应音频水印算法，根据音频信号的质量最佳即信噪比取最大值为约束条件对LWT 分解后的低频系数进行缩放，通过量化范数比动态地在音频信号中嵌入水印。仿真结果证明，本文算法具有有效性和可靠性。

1 算法的主要技术与原理

1.1 LWT

LWT 是一种新的在时域中采用提升方法构造小波的第二代小波算法。它对原有的小波变换算法做出改进，是一种更加快速有效的手段。

LWT 具备以下优势：

（1）不依赖于傅里叶变换，在时域中实现对双正交小波的构造，具有结构化设计和自适应构造方面的特点；

（2）构造方法灵活，可以用简单的小波函数，通过提升改善小波函数的特性，构造具有期望特点的小波；

（3）算法简单，运算速度快；

（4）占用内存少，执行效率高，可以分析任意长度的信号。

LWT 过程包括分解、预测和更新3 个步骤。通常，在MATLAB 中运用LWT 的主要过程如下：

（1）先用小波函数得到与之相对应的提升小波方案；

（2）设置原始的提升步骤，把提升步骤添加到提升方案；

（3）应用提升方案对向量进行提升小波变换。

LWT 把信号进行一级分解后会得到低频分量cA1和高频分量cD1。低频分量cA1可以继续进行分解，得到低频分量cA2和高频分量cD2。经过n级LWT 分解得到的低频分量cAn的能量最大，最具有鲁棒性。通常，把水印信息嵌入到经过LWT 分解的低频分量中。

1.2 向量范数

向量范数的鲁棒性可以用来嵌入水印。假设A=(a1,a2,…,an)是一个1×n的向量，σ是A的向量范数，定义如下：

1.3 量化算法原理

假设要量化的系数为f，量化步长为e，量化后的对应系数为f´，要嵌入的水印比特为w，取值为0 或1，则量化算法嵌入水印原理如图1 所示。

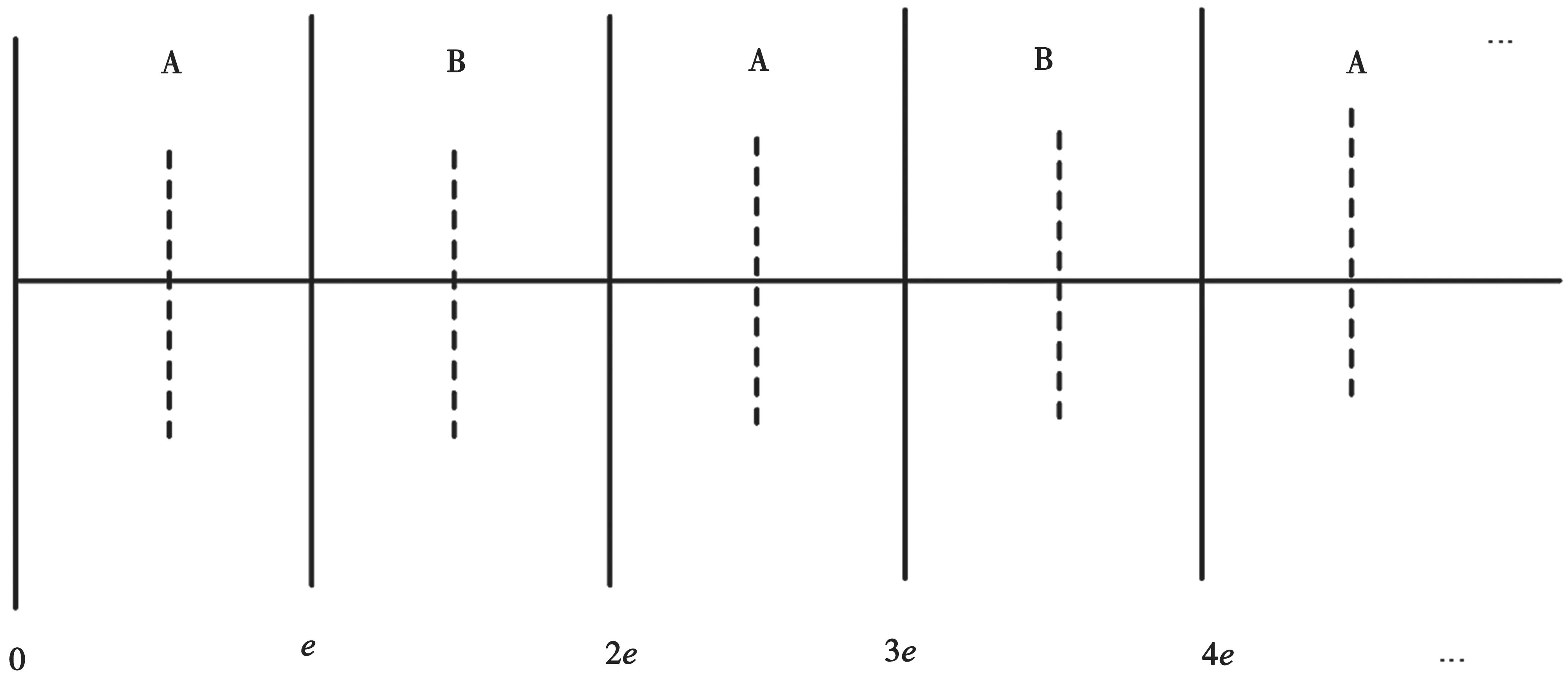
图1 量化算法嵌入水印原理

第1 步：根据量化步长e将坐标轴上所有区域分成A 区间集和B 区间集。其中，只要是A 区间集的坐标都表示1，只要是B区间集的坐标都表示0。

第2 步：对待量化系数f，按照式（3）和式（4）进行运算：

第3 步：量化操作。

（1）当m=0 且w=1 时，有：

（2）当m=0 且w=0 时，有：

（3）当m ≠0 且w=1 时，有：

2 基于范数比的LWT 域自适应音频水印算法

2.1 水印预处理

水印图像在嵌入到音频信号之前需要经过预处理，降低图像像素之间的相关性，以提高水印系统的安全性[14]。假设水印图像表示为W={W(i,j),1 ≤i≤M,1 ≤j≤N}，其中W(i,j)∈{0,1}为水印图像第i行、第j列的像素值，M为像素的行数，N为像素的列数，则对水印图像进行如下的预处理操作。

（1）对原始二值水印图像W进行K次Arnold变换，降低原始水印像素之间的相关性。

（2）对Arnold 变换后的图像进行Logistic 混沌序列加密。由于Arnold 变换具有周期性，在现有的计算条件下有可能采取穷举法破解水印，因此对水印图像进行混沌加密处理。生成一个长度为M×N的Logistic 混沌序列，设定一个阈值，将序列内所有元素都转化为0 或1，然后与降维后的水印图像异或运算进行加密。Arnold 变换和Logistic 混沌序列的参数可以作为提取水印时的密钥。只有知道密钥，才能对水印信息正确解密。

2.2 水印嵌入过程

本文提出基于范数比的LWT 域自适应音频水印算法，对原始音频信号分帧后进行LWT 分解，然后把得到的低频系数分成两部分分别计算范数，通过量化范数比来实现嵌入水印的目的。根据音频信号的质量最优即信噪比取最大值为约束条件，对低频系数进行缩放。水印嵌入过程流程如图2 所示。

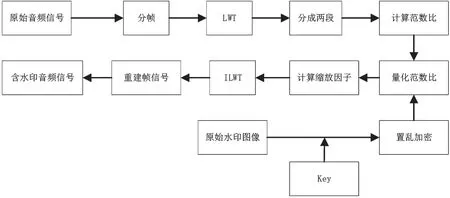
图2 水印嵌入过程流程

水印嵌入的具体步骤如下。

第1 步：记原始音频的采样点数为L，把原始音频信号分成不重合的M×N帧，这里的帧数和水印图像的比特数保持一致，使每帧音频信号都嵌入1 bit 水印信息，然后对每帧音频信号进行LWT 分解。这里的级数为3，低频分量记为Ci(j)，i代表帧数，j代表低频分量的长度，1 ≤j≤Lc，其中Lc=L/(M×N×23)。

第2 步：把低频系数Ci(j)平均分成两部分，第一部分表示为Ci,1(j)，第二部分表示为Ci,2(j)，按照 式（1）计算它们的向量范数，分别表示为σi,1和σi,2。

第3 步：计算范数比ρi=σi,1/σi,2，使用1.3 节介绍的量化方法求出量化后的范数比。

第4 步：将低频系数Ci,1(j)和Ci,2(j)分别用缩放因子α1和α2进行缩放。这里，缩放因子α1和α2按照后面给出的步骤优化，修改低频系数，

信噪比（Signal Noise Ratio，SNR）是用来衡量音频信号质量的重要指标，公式如下：

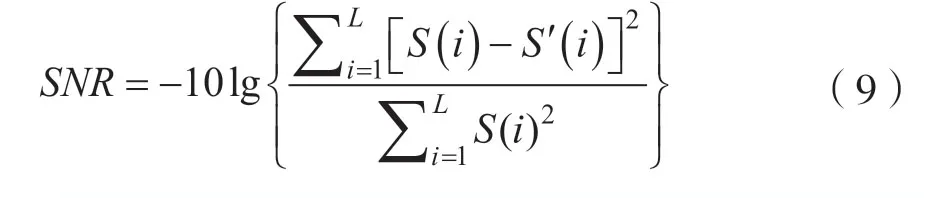
式中，S(i)代表原始音频信号的采样点，S´(i)代表嵌入水印后的音频信号采样点。

由于嵌入水印的过程中使用正交小波，因此信噪比在小波域的相关指标可以表示为：

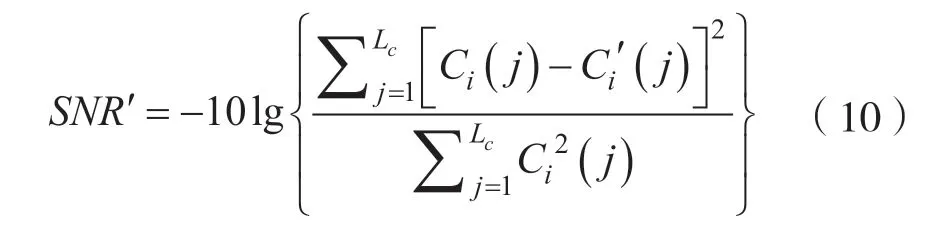
式中，Ci(j)和是对应的LWT 系数。把它们用向量范数{σi,1,σi,2}和缩放因子{α1,α2}表示，该性能指标可以转化为：

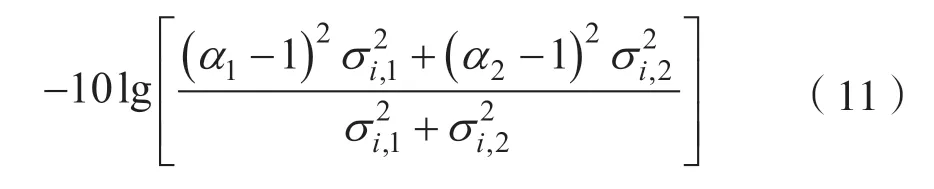
使音频的质量保持最优，即信噪比取最大值，这就相当于式（11）中进行对数运算的部分有最小值，等价于式（12）有最小值：

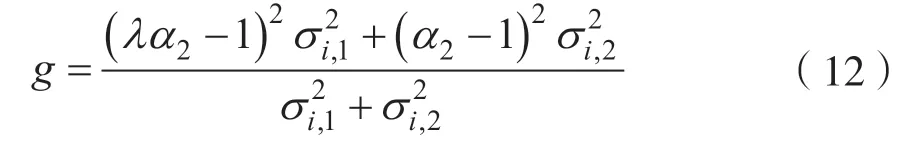
对式（12）求导，有：

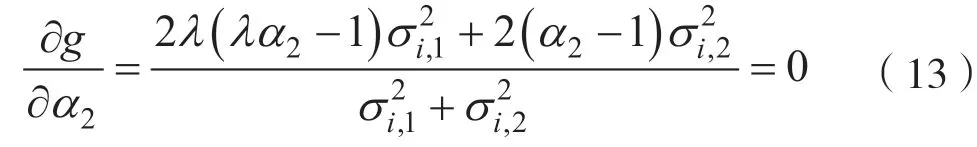
求得尺度因子α1和α2：

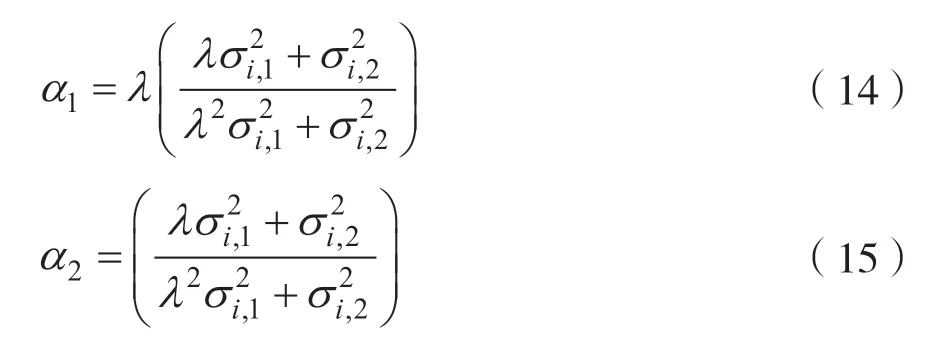
第5 步：利用缩放因子α1和α2改变低频系数Ci,1(j)和Ci,2(j)的值，再经过信号重构获得每一帧信号，最后组合成含水印的音频信号。

2.3 水印提取过程

水印提取过程的流程如图3 所示。

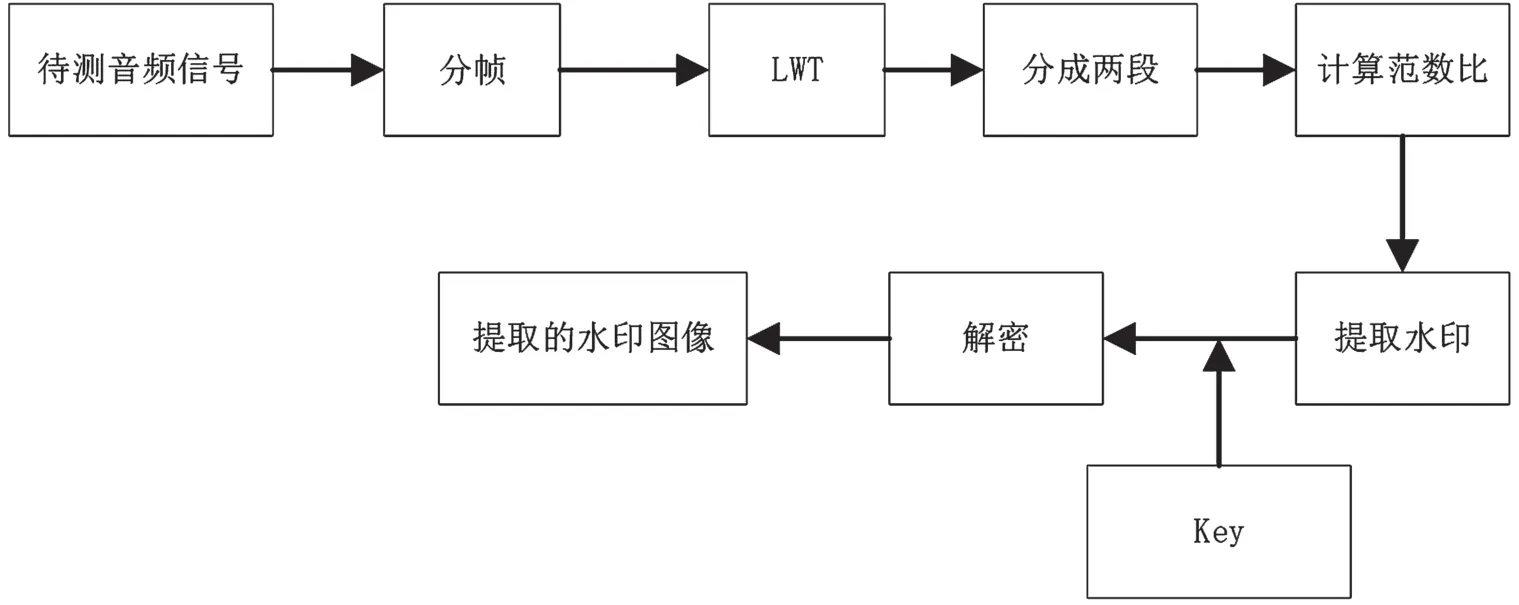
图3 水印提取过程流程

水印提取过程的具体步骤如下。

第1 步：将待测音频信号分成不重合的M×N帧，对每帧音频信号进行3 级LWT 分解获得低频系数，然后分成两段分别计算向量范数，分别记为。

第3 步：将提取的水印信息根据Logistic 混沌序列和Arnold 变换的参数进行解密，得到提取出的水印图像。

3 实验结果分析

为了验证本文算法的有效性，采用的计算机为Windows 10 操作系统环境，实验仿真平台为MATLAB 2018，对乡村音乐、流行音乐和语音3 类音频进行测试。音频均为wav 格式，线性PCM 编码，采样率为44.100 kHz，16 位单声道，每段音频包含1 048 576 个采样点。提升小波方案采用haar 小波，提升步骤为{‘p’,[-0.125 0.125],0}。

3.1 水印的安全性分析

选用大小为32×32 的二值图像作为水印，内容是一个汉字“卓”。在ASCII 码中，表示一个汉字需要16 bit，而选用的图像占1 024 bit，可见在增大信息冗余的角度提高了水印的鲁棒性。对于水印的预处理，Arnold 变化的次数为10，生成Logistic混沌序列的μ为3.9，初始值x0为0.418。水印图像经过置乱和加密后的结果如图4 所示。

从图4 可以看出，经过Arnold 变换和Logistic混沌加密，图像像素之间的相关性被破坏，只有知道密钥才能对其解密。

图4 水印置乱及加密

3.2 水印的不可感知性分析

3.2.1 主观评价

通过观察音频信号在嵌入水印前后波形的变化，能对嵌入水印后音频的不可感知性有一个大致认识。图5 是乡村音乐在嵌入水印后的波形图。从图5 可以看出，嵌入水印后波形差别不大，说明嵌入水印后造成的影响非常小。

图5 嵌入水印前后波形比较

3.2.2 客观评价

信噪比（SNR）作为不可感知性的客观评价标准，国际留声机工业联盟要求嵌入水印后的音频至少要达到20 dB 的信噪比。3 类音频的信噪比如 表1 所示。

表1 不同类型音频信号的信噪比

3.3 鲁棒性分析

鲁棒性用来衡量在音频信号中添加水印后的抗攻击能力，有相关系数（Normalized Correlation，NC）和误码率（Bit Error Rate，BER）两个指标衡量。

NC 指的是提取的水印和原始水印之间的相关程度。NC 的值越接近于1，表明二者的相关程度越高，计算公式如下：

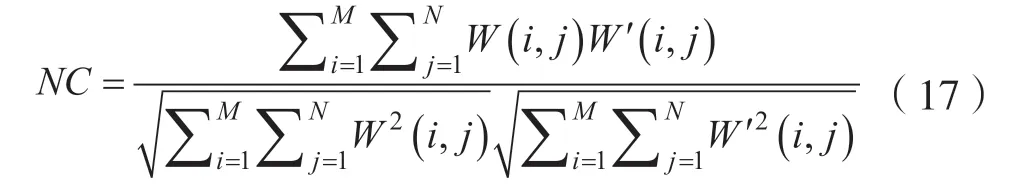
式中，W表示原始水印，W´表示提取的水印。

BER指的是从含水印音频中提取的水印和原始水印之间的差异程度。BER的值越接近于0，说明水印系统的鲁棒性越好，定义如下：

为了验证本文提出算法的鲁棒性，对含水印音频进行如下信号处理操作。

（1）添加噪声：在含水印音频信号中添加信噪比为20 dB 的高斯白噪声。

（2）低通滤波：采用巴特沃斯滤波器对含水印音频信号进行滤波，截止频率为11.025 kHz。

（3）重采样：把含水印音频信号的原来44.100 kHz 的采样率降为22.050 kHz，然后再恢复至44.100 kHz。

（4）重量化：将16 bit 的含水印音频信号重新量化为8 bit，然后再恢复为16 bit。

（5）MP3 压缩：将含水印音频信号由wav 格式转换成mp3 格式，再恢复至wav 格式，比特率为128 kb/s。

表2 列出了3 种类型的含水印音频信号在遭到信号攻击后的NC值和BER值。

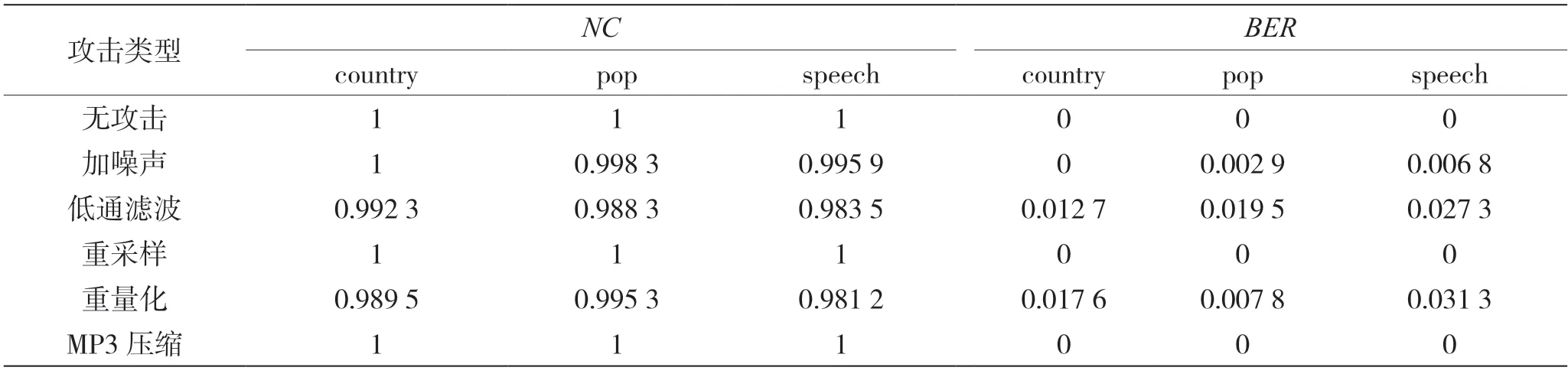
表2 不同类型音频的鲁棒性

从表2 可以看出，在整个测试过程中得到的BER值都非常小，不大于0.031 3，大部分情况下接近于0，得到的NC值都不小于0.981 2，大部分情况下接近于1，说明本文算法对常见的音频信号攻击表现出良好的鲁棒性。

为了进一步说明本文算法的鲁棒性，与近期的一篇相似文献[10]进行对比，选用乡村音乐以及同样的水印信息进行实验，对比实验结果如表3 所示。表3 给出了本文算法提取的水印，从相对高的NC值和相对低的BER 值可以看出，本文算法的鲁棒性优于文献[10]提到的算法。

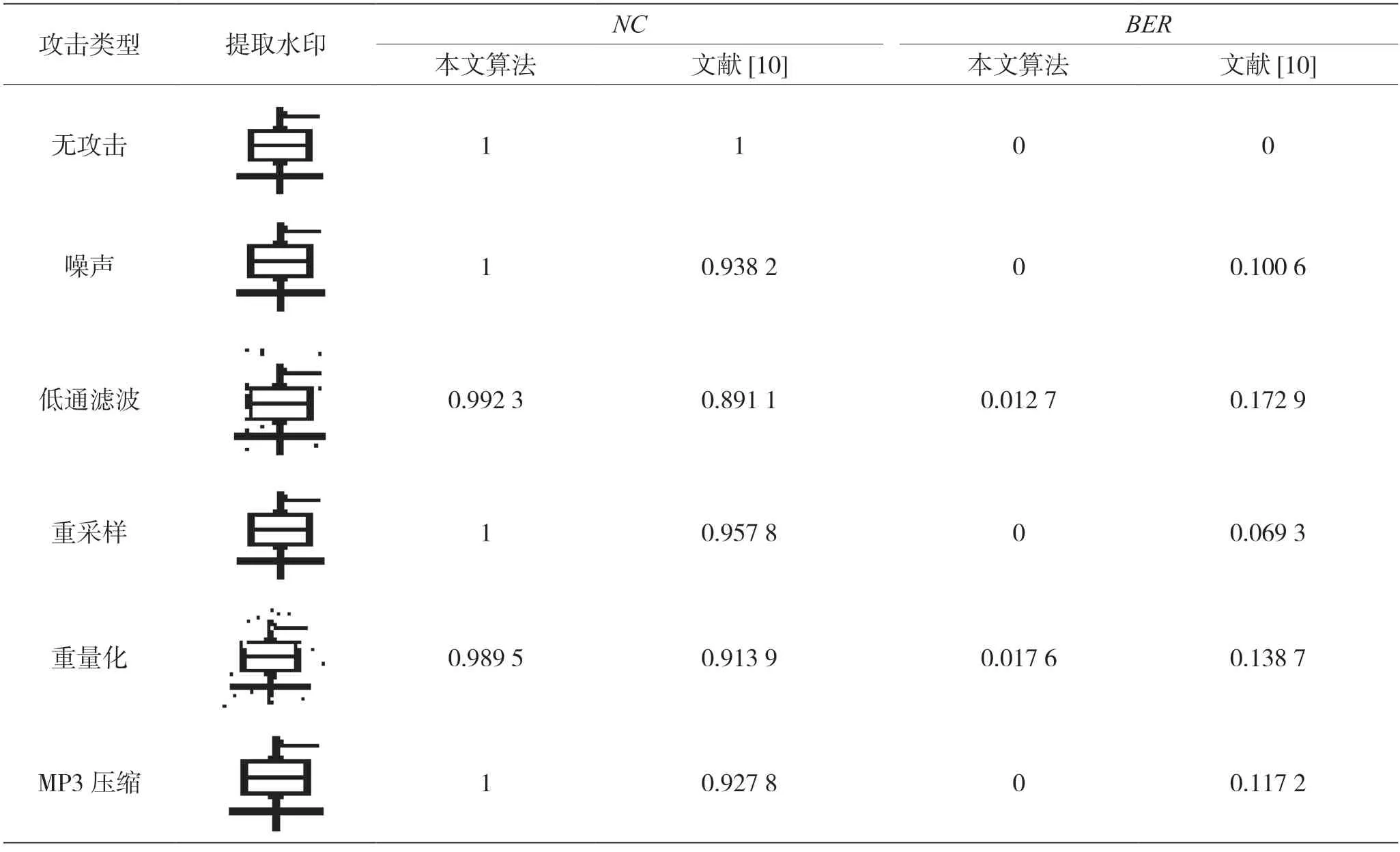
表3 不同算法鲁棒性比较

3.4 水印容量分析

水印容量指单位时间的音频信号中嵌入水印的比特数，单位为比特每秒（b/s），计算公式如下：

式中：fs表示音频信号的采样率；L代表音频信号的采样点数；n表示水印的像素点数。国际留声机工业联盟要求水印容量不小于20 b/s。在本文所提的算法中，水印容量为43.07 b/s，符合要求。

4 结语

本文提出了一种基于范数比的LWT 域自适应音频水印算法，能够实现对水印的盲提取，选取二值图像作为水印信息，从增大信息冗余的角度提高了水印系统的鲁棒性。另外，通过Arnold 变换置乱和Logistic混沌序列加密提高了水印系统的安全性。实验结果表明，本文算法有较好的不可感知性，达到水印嵌入容量的要求，在抵抗添加噪声、低通滤波、重采样、重量化和MP3 压缩等信号攻击时，表现出良好的鲁棒性。