基于小波变换投影的卫星动态信道化接收技术研究*

张渊博，郭道省，陈祝允

（陆军工程大学，南京 江苏 210007）

0 引言

随着通信技术的发展，卫星通信技术在通信领域起到了举足轻重的作用。卫星通信由于其通信带宽覆盖范围广、稳定性好的特点被广泛应用于：卫星电话业务、数据传输业务、电视转播业务、移动通信业务、应急救援及远程医疗等[1]。在宽带卫星通信中常采用频分多址（Frequency Division Multiple Access，FDMA）或多频时分多址（Multi-Frequency Time-Division Multiple Access，MF-TDMA）等技术[2]，为了使上行信道里的多个用户信号分别转发到不同的下行信道中，从而达到交换路由的目的，卫星信道化技术由此诞生。一般情况下，通信用户的数量是随机的，并且用户占用频带通信时，调制方式多样且占用的频带范围随机变化，使信道化过程中对子带信号的处理过程变得复杂，因此在宽带卫星通信中，关于动态信道化接收机的研究成为了研究热点[3]。

有关学者针对信道化接收机进行了大量研究。文献[4]对宽带数字信道化接收机的发展做出了很好的阐述。文献[5-6]描述了基于复指数调制滤波器组的信道化实现结构及过程，相比于余弦调制方式下的滤波器组，基于复指数调制的滤波器组能够对复数信号实现有效的信道化过程。文献[7-8]针对连续相位变化的信号进行动态信道化接收机技术展开研究，分别提出了结合短时傅里叶变换的多相分解实现结构和并行结构的数字信道化接收机，提高了信道化接收机的处理效率。针对动态信道化过程中子带信号检测辅助信道化的过程，文献[9]用短时傅里叶变换（Short-Time Fourier Transform，STFT）局部累计量作为检测的手段对子带信号进行检测，实现了动态信道化过程。文献[10]利用能量检测作为辅助，研究动态信道化接收技术。文献[9]和文献[10]在低噪声能量信道环境下完成了动态信道化接收的过程，但低信噪比环境下，其子带信号检测过程不准确，不能有效地实现信道化过程。

本文对低信噪比环境下的宽带卫星动态信道化过程进行优化，提出了一种基于小波变换投影的动态信道化算法，即采用小波变换系数投影检测，将不同小波平移量下的小波检测系数投影到同一频域中。该算法弱化了高能量随机噪声对检测结果的影响，使得子带信号检测的曲线更加平滑，提高了信道化重构前子带信号检测的准确率。仿真结果表明，在低信噪比下，所提算法在动态信道化过程中性能表现优于STFT 局部累积量算法与能量谱密度。

1 复指数调制滤波器组高效实现结构

在宽带卫星通信系统中，信道化过程是通过滤波器组分析和重构宽带信号来实现的。其基本结构分为分析滤波和综合滤波。传统的信道化技术是根据宽带信号的频谱分布情况，设计不同带宽和不同中心频率的滤波器组来实现整个过程。然而，一般宽带卫星通信的子带信号具有分布较为密集、检测带宽大的特点，且滤波器组的设计需要极高的成本和硬件条件。因此，根据不同子带信号的特点，设计一种具有自适应特性的滤波器组结构，降低对硬件条件的依赖，是信道化技术中研究的关键。

复指数调制滤波器组是通过复指数调制技术对原型滤波器进行调制后获得的，其与余弦滤波器组有一定的区别。文献[5]描述了两者之间的联系与区别。余弦调制的滤波器组得到的系数为实数，而复指数调制滤波器组获得的系数为复数。余弦调制滤波器组在接收复数信号后输出的信道化结果会产生频率分量的混叠，而复指数调制滤波器组的设计很好地解决了混叠信号的产生，但复指数调制滤波器组的分支比余弦调制滤波器组多出一倍。复指数调制的基本结构如图1 所示，分为分析滤波部分和综合滤波部分。

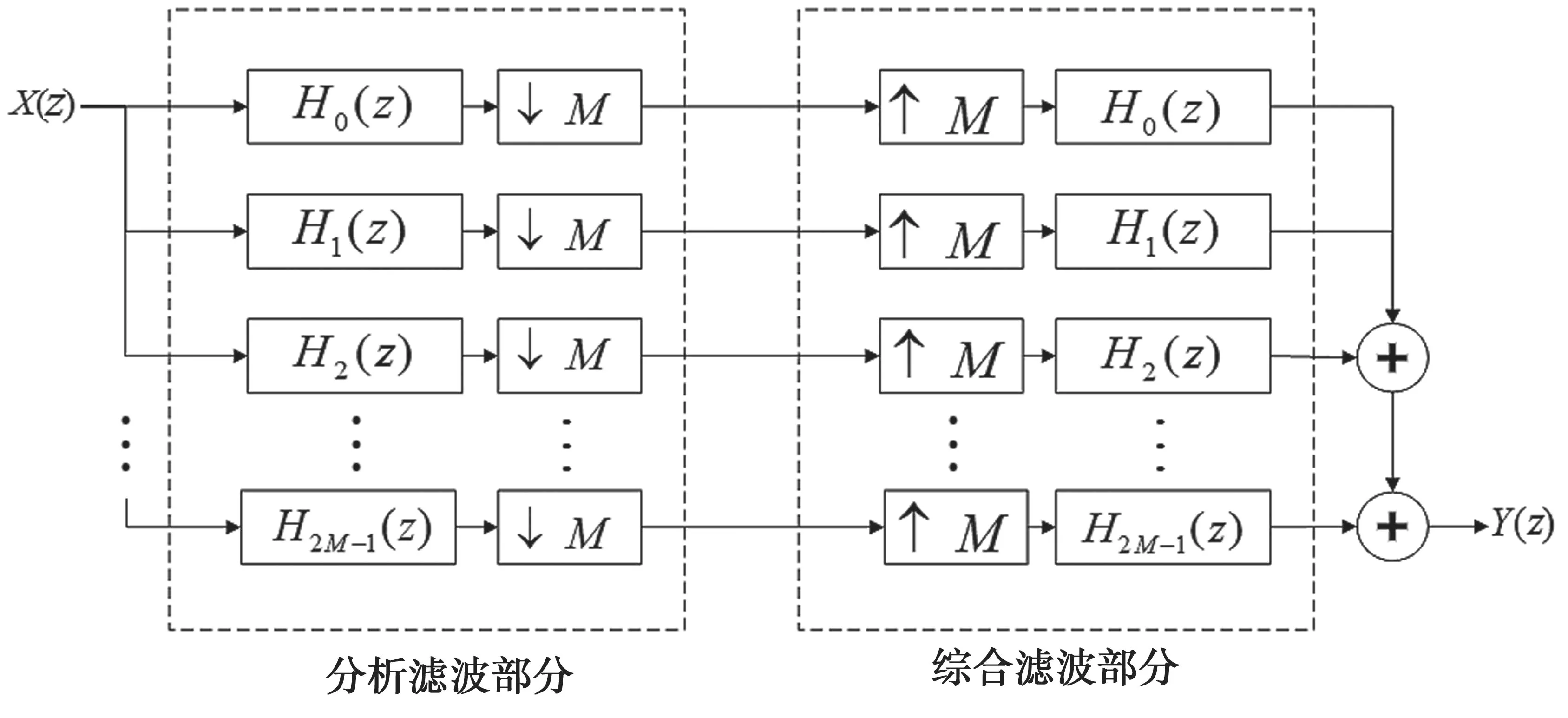
图1 复指数滤波器组的基本结构

在卫星通信系统中，调制方式会将实数信号转换为IQ正交的复数信号，复数信号表示为X(z)：

式中，I为信号的同相分量，Q为信号的正交分量，j 为虚数单位。卫星信号接收器接收的宽带信号包含子带信号的数量为N，第i个子带信号为Xi(z),i=0,1,…,N-1，其频谱响应满足：

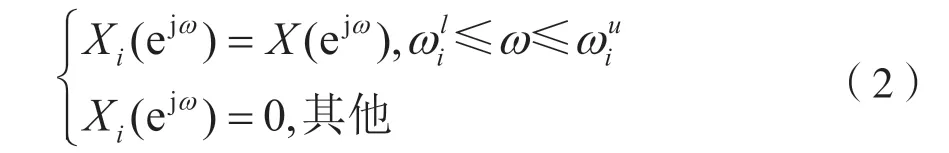
式中，和分别为子带信号占用频率的下界与上界，相邻子信道的保护带Gmin定义如下：

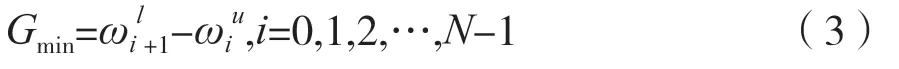
不同子带信号保护带相等，且满足条件-=2π，通过Gmin可以得到滤波器组划分的数量2M，M满足如下条件：

文献[11]通过一种基于二通道无损格型的原型滤波器组的设计方法。构造出原型滤波器H(z)的两个多相分量Eq(z)和HM+q(z)其构造方法为：

将式（8）整理推导后可得：

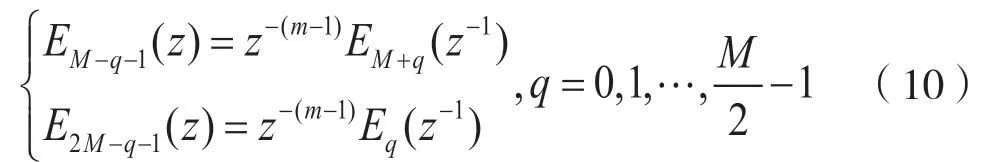
m的值由原型滤波器的阻带衰减有关[5]。最终获得H(z)，为：

优化过程中参数θq,p可以给定初值：

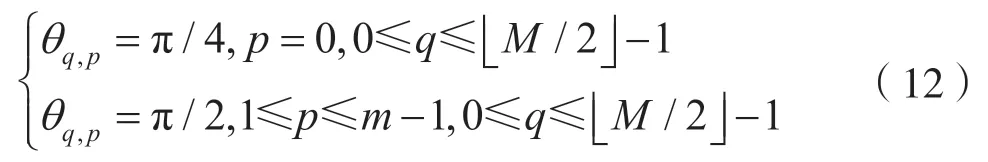
将所有给定的参数θq,p代入H(z)的2M个同相分量，从中得到频率响应H(ejω)，代入式（13）和式（14）得到优化后的Φ1和Φ2，其计算值为：

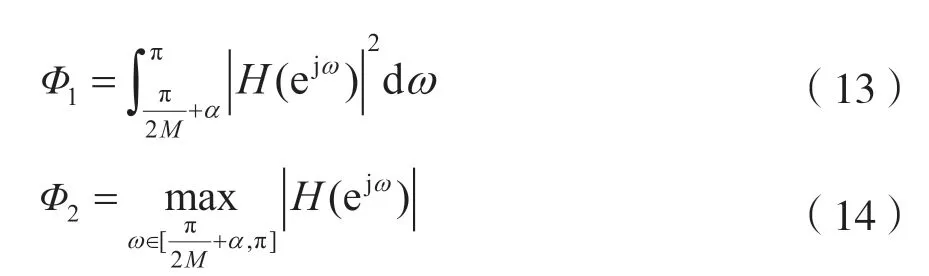
式中，α=[0,π/(2M)]。由此，可得精确的重构滤波器h(n)，阻带衰减为As，阻带边缘为ωs=π/M。则系数长度为2mM的原型滤波器h(n)对应的基于复指数调制的滤波器组表达式为：

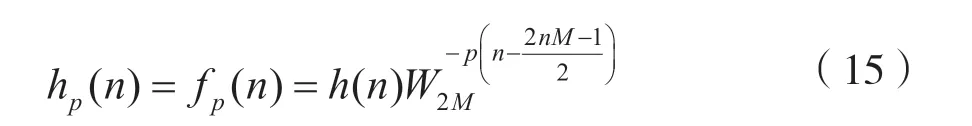
式中，WM=e-j2π/M,n=0,1,…,2M。

文献[12]证明，滤波后抽取的实现过程可以与先滤波后抽取的结构相互转化且相互等效，其等效结构如图2 所示。

图2 抽取器与滤波器级联的等效结构

从图2 的左半部分可得输入输出关系：

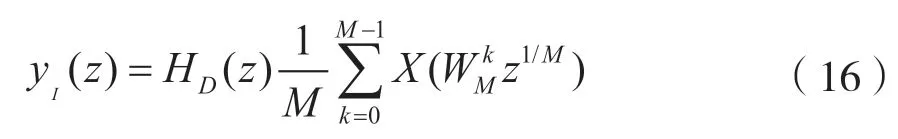
同理其右半部分输入输出关系为：

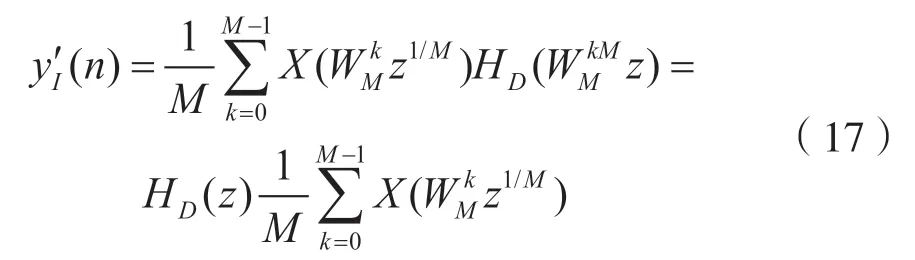
由式（16）、式（17）可知，两种结构是可以等效替代的，调整为抽取后滤波的分析滤波结构和内插后滤波的综合滤波结构后，可以有效提高运算效率。因此，图1 的基本实现结构可转化为如图3所示的结构，二者相互等效。

图3 复指数调制滤波器组实现结构

2 基于小波变换投影的子带信号检测

假设宽带信号没有任何交换、转发和广播环节，图3 的基于复指数滤波器组信道化结构能够满足最基本的信道化需求。然而，在现在的宽带卫星通信系统中，一般都需要很多转发、广播等业务，这就对信道化技术研究提出了动态化要求，使其适应当前动态接收和转发的需求。针对第1 部分分析的基于复指数调制滤波器组模型，提出了一种基于小波变换投影检测子带信号的方法，实现了动态信道化的过程。假设在宽带卫星通信系统中输入信号的x(n)有p个子带信号，图4 为基于小波变换系数检测的动态信道化结构。

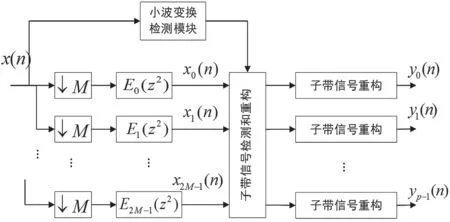
图4 基于小波变换检测的动态信道化结构

图4 中小波变换检测模块的功能是对输入信号x(n)进行小波变换投影。当信号为时域连续信号f(t)，此模块对信号做小波变换得到小波变换的 系数：

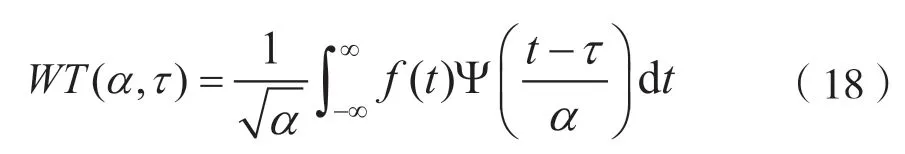
式中：WT(α,τ)为得到的小波变换系数；α为小波变换尺度，控制小波函数的伸缩，对应了信号的频率值；τ为小波平移量，控制小波函数的平移量，对应了时域位置；Ψ表示小波基函数。频率和变换尺度的对应关系满足：

式中：Fc为小波变换的中心频率，fs为采样率。变换尺度越大，对应的频率值越低。

小波变换与傅里叶变换相比，将无限长的余弦基函数替换为有限长度的衰减函数。由于小波变换有两个变换量α和τ，通过小波变换不仅可以知道信号有哪些频率分量，并且可以知道对应的频率在时域上的位置信息，文献[13]对小波变换等多种时频分析方法作了详细的论证。

由上述小波变换公式和频率与变换尺度的关系，可以得：

将小波变换后得到的关于频域f和变换尺度τ的变换系数投影到一维变换函数w(f)，其投影关系满足关系：

式中，τ0∈(0,T),τ∈R，T为信号采样时间。

子带信号检测和重构模块负责对输入信号的小波变换进行检测，针对小波系数的判决结果，每个子带信号进行重构。子带信号检测和重构实现步骤如下所示。

（1）计算归一化的小波变换投影系数。

归一化后的小波变换投影系数w(f)满足：

最终对时域连续信号f(t)进行小波变换投影且归一化系数后得到的结果为

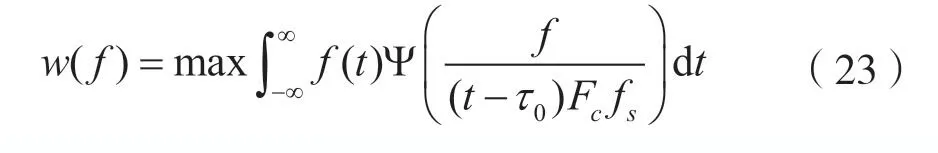
（2）计算无信号状态下的噪声小波变换系数。

卫星通信系统中，接收机接收到的信号是由用户发送的信号和噪声信号共同构成的，满足：

式中，s(t)为用户发射的无噪声信号，n(t)为高斯白噪声。在无信号发送下的小波检测结果满足：

代入推导的小波系数投影关系及小波变换公式可得：

式中，τ0∈(0,T),τ∈R，T为信号采样时间。

（3）设置子带信号检测判决阈值。

通过步骤（2）无信号状态下的小波变换系数，检测判决子带信号是否存在的门限可以设置为纯噪声小波变换系数的均值，判决门限th满足：

式中：λ为加权系数，取值区间为[2,3]；B为检测频段的带宽；fl和fu分别为检测频段的上界和下界，且带宽和上下界满足关系B=fu-fl。

（4）对接收的宽带信号进行检测和判决。

在获得信号的小波变换系数和判决门限之后，通过式（27）判决子带信号是否存在。

根据式（28）的判决结果即可检测频段内是否存在子带信号，及存在的子带信号所对应的频率值，为信道化过程中子带信号的重构提供了保证。此外，利用小波系数投影的方法，可以将对子带信号判决结果无关的小波平移量τ上的所有小波变换系数都投影到同一频域上，从而降低了高能量的随机噪声对于信号检测的影响，投影后使得小波检测获得的小波系数更加平滑。在低信噪比条件下，与传统的能量检测算法和STFT 局部累积量进行的子带信号检测方法相比，通过小波系数投影检测，其子带信号表现出的信号特征与噪声特征差异性更大，极大地提高了子带信号检测的准确率，为信道化重构奠定了基础。

3 仿真和分析

参照文献[5]，使用MATLAB 仿真软件设计了一个32 通道的复指数调制滤波器组，使用小波变换检测并判决宽带信号，实现了对宽带信号的动态化信道过程。仿真相关的参数如下所示：仿真中宽带信号的频率范围为0～60 MHz，采样率为 120 MHz，信噪比为0 dB。假设在接收过程中有两种情况：第1 种状态包含了4 个子带信号，其分布为7～9 MHz、20～23 MHz、32～36 MHz、49～ 55 MHz；第2 种状态包含了5 个子带信号，其分布 为7～9 MHz、17～20 MHz、26～30 MHz、37～43 MHz、51～55 MHz。采用高斯最小频移键 控（Gaussian Filtered Minimum Shift Keying，GMSK）调制方式。小波变换长度L=1 200，小波变换尺度α=600。两种状态宽带信号信化接收结果如图5 和图6 所示。

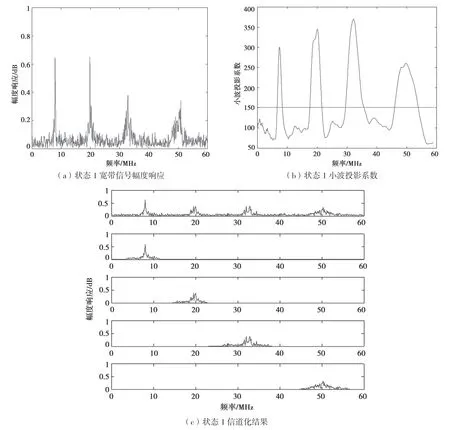
图5 状态1 宽带信号的信道化结果

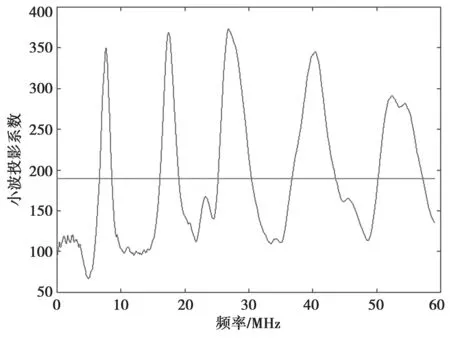
图6 状态2 宽带信号的信道化结果

如图5 和图6 两图所示，通过小波变换系数投影检测子带信号，对于信号和噪声的区分度更大。如图7 所示，在低信噪比为0 dB 条件下明显优于STFT 局部累积量，更加有利于对子带信号的检测。当输入的宽带信号的状态发生改变时，基于小波变换系数投影的信道化结果能够很好地适应宽带信号的变化，并且在盲信道化的过程中有良好的表现。仿真结果显示基于小波系数投影检测的动态信道化过程在低信噪比条件下性能表现优于STFT 局部累积量检测算法与能量检测算法。

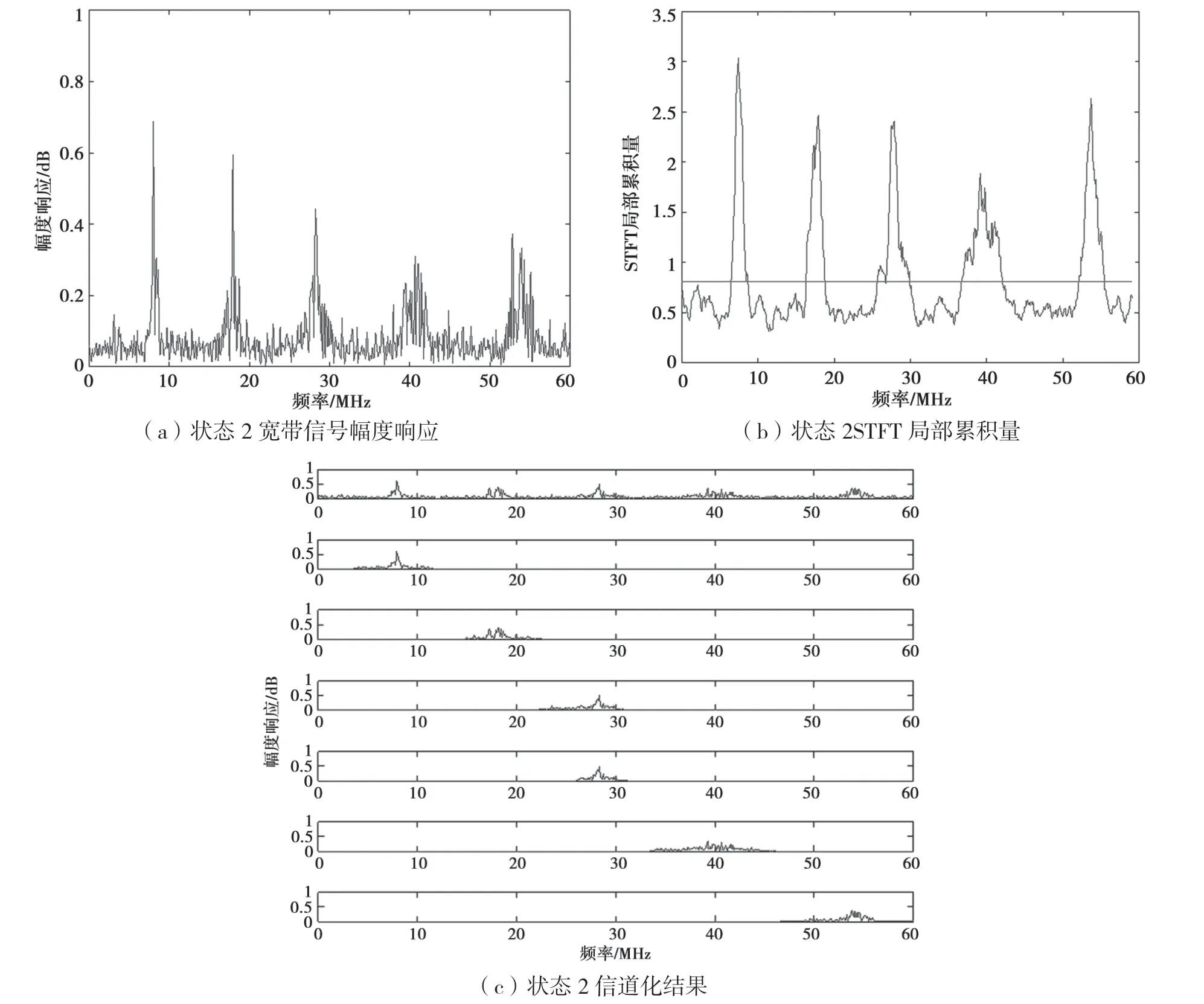
图7 状态2 利用STFT 判决的信道化结果

在仿真过程中，为了进一步验证本文算法在不同信噪比下信道化结果重构成功率，即准确将收到的一个宽带信号内的多个子带信号分离成多个独立窄带信号，且分离后的窄带信号与原子带信号所在的频谱位置一致的概率。设置了1 000 次的蒙特卡洛实验，在-5 dB 到10 dB 的信噪比条件下与STFT局部累积量和能量谱密度检测进行了对比，其结果如图8 所示。

如图8 所示，基于小波投影检测的动态信道化算法在不同信噪比下均优于STFT 局部累计量算法与能量谱检测算法。在信噪比为4 dB 时，本文算法实现的信道化结果成功率高于95＆，相比于能量谱检测的70＆成功率和STFT 局部累积量的50＆的成功率有了明显的提升。对比结果显示了基于小波投影检测的动态信道化算法在低信噪比环境下的优异性能。

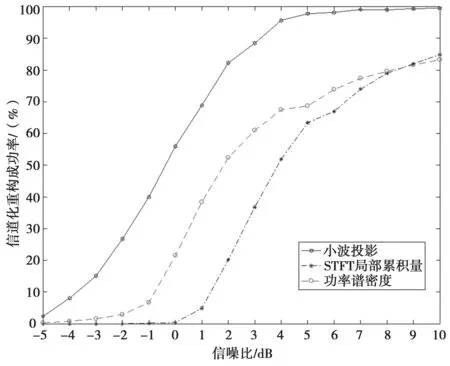
图8 不同信噪比下不同算法的重构成功率曲线

为了进一步证实本文方法的可行性及性能表现，本文引入重构误差来分析原信号和重构后的信号的差异性。假设有p个子带信号，将子带信号的输出综合可得所有子带信号的输出为：

所有子带信号的输出的频谱响应可以表示为：

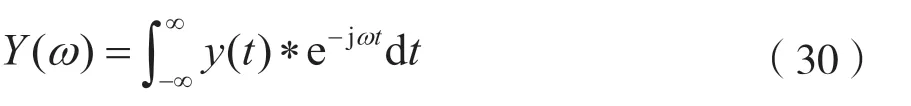
定义信道化系统重构误差为：

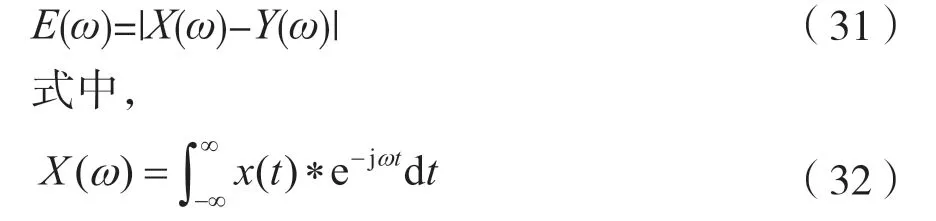
两种状态下的宽带信号的重构误差如图9和图10所示。

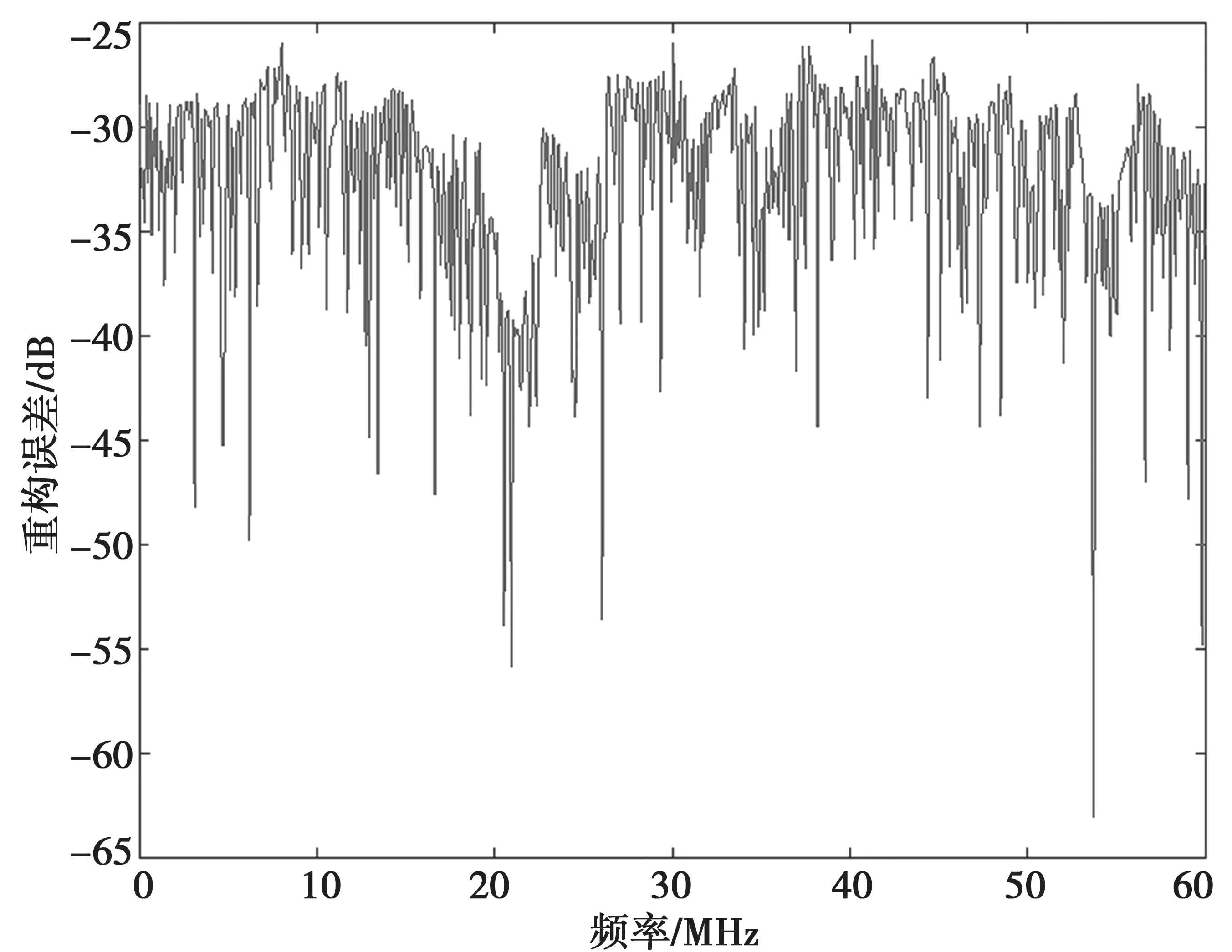
图9 状态1 的信道化重构误差

从图9 和图10 可以分析得到，两种状态的宽带信号在信道化过程中的重构误差均小于-25 dB，远小于通信系统的噪载比-10 dB，重构误差几乎可以忽略不计。因此，本文所描述的动态信道化的方法，满足了宽带卫星通信系统的要求，具有可行性。

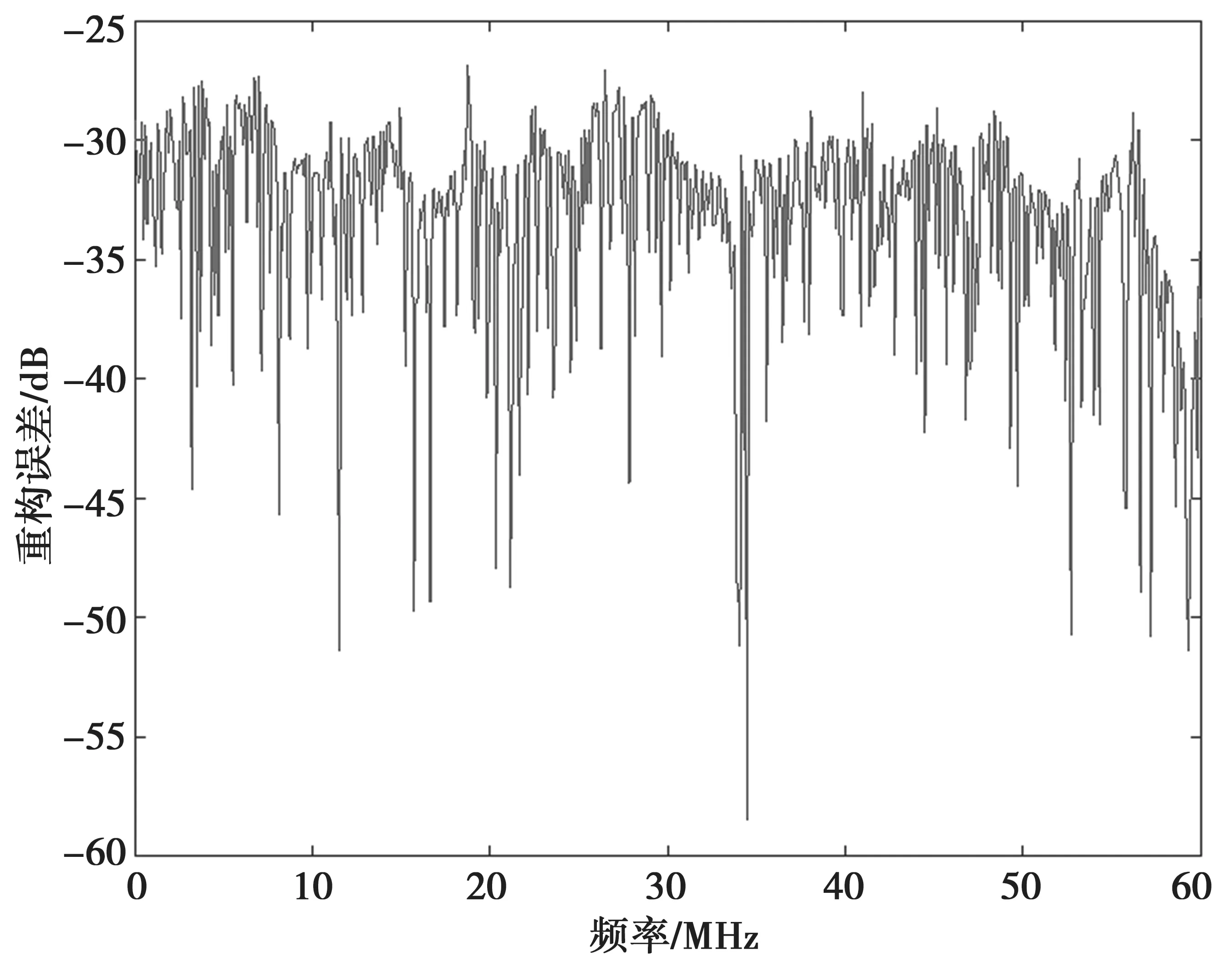
图10 状态2 的信道化重构误差

4 结语

本文详细分析了基于复指数调制滤波器组的信道化处理基础结构，提出了基于小波变换投影动态信道化实现方案。该方案针对没有先验信息的宽带信号进行检测，实现了盲信道化过程，为信道化过程的重构环节奠定了基础；利用小波变换系数投影对时域信号进行分析，增大了信号与噪声的差异性，在低信噪比下的性能表现明显优于能量检测算法和STFT。此外，本文算法实现复杂度低，逻辑结构清晰，能够适应卫星通信系统对于信号的快速处理的要求，具有高效性，为下一代信道化接收机的发展提供了理论参考。最终的仿真结果显示了基于小波投影检测动态信道化的算法的有效性。