SRP-NMF:一种多通道盲源分离算法*
皮 磊,郑 翔,武欣嵘,陈美均
(陆军工程大学,江苏 南京 210007)
0 引言
鸡尾酒会问题[1]是一个经典的盲源分离问题,其目的是从混合信号中将源信号分离出来。然而,这样一个对人类来说毫不费力的任务,对于计算机来说却十分困难。盲源分离技术虽然已经经历了很长一段时间的研究,但目前仍然是计算机和信号处理领域的研究热点和难点。
大部分盲源分离算法可分为单通道盲源分离算法(M=1)和多通道盲源分离算法(M≥2)[2],其中M表示麦克风数量。
在多通道盲源分离问题中,假设在源信号数量为K和麦克风数量为M,则混合信号xt可以表示为:

式中:xt=[x1,t,x2,t,…,xM,t]T为M个麦克风混合信号向量;A为M×K维的未知混合矩阵;st=[s1,t,s2,t,…,sK,t]T为K个未知的源信号向量;nt为M维的噪声向量,其中t为时间索引。
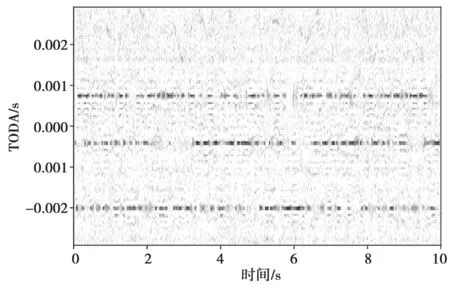
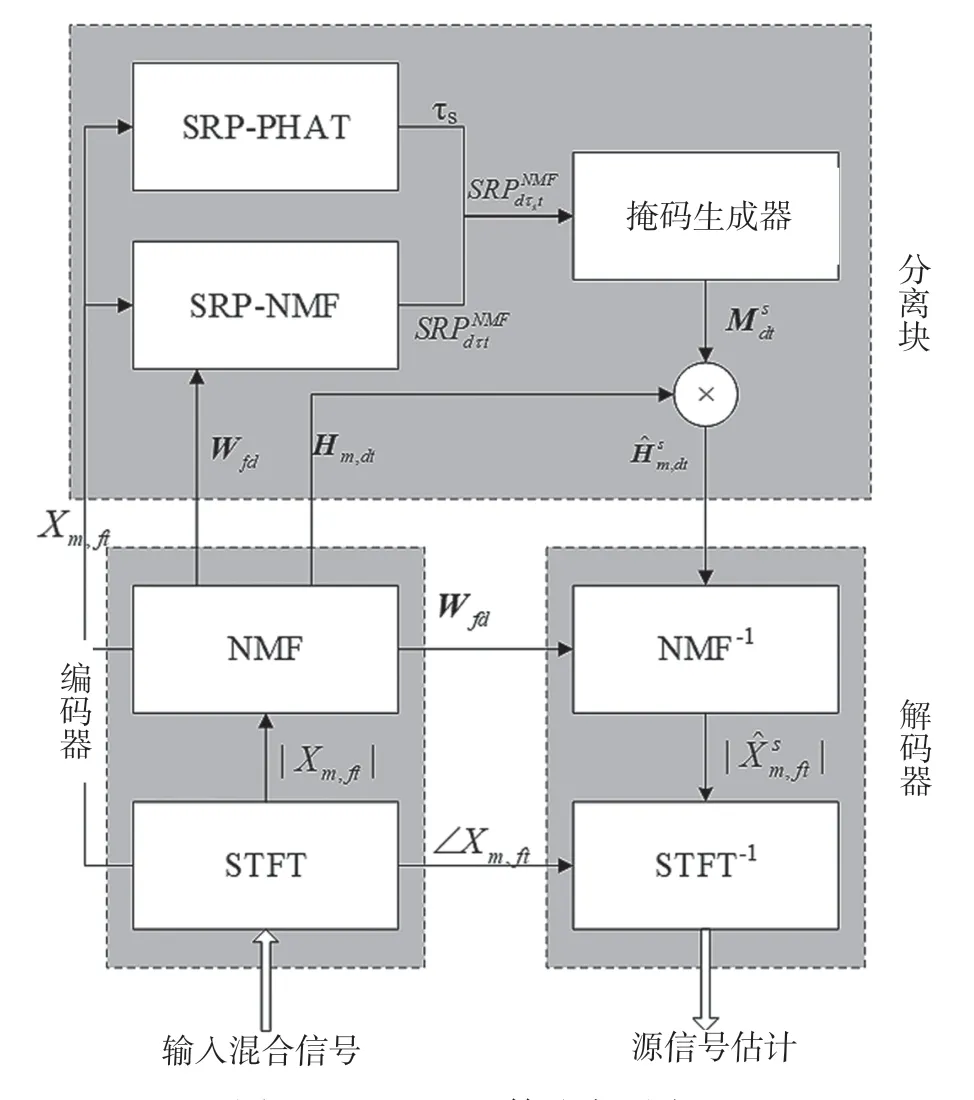
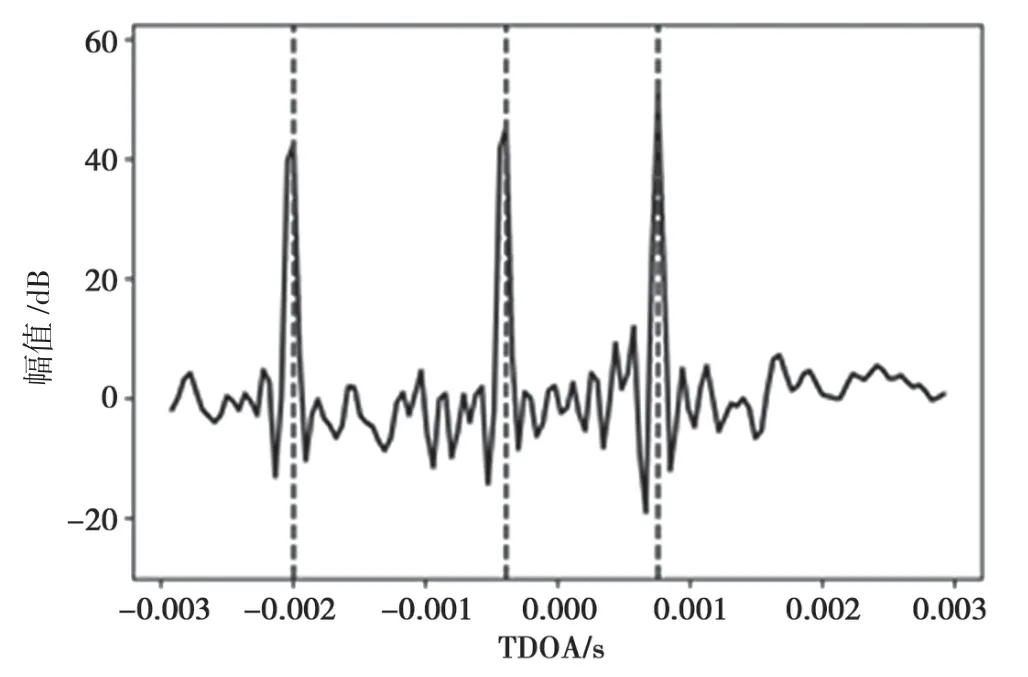
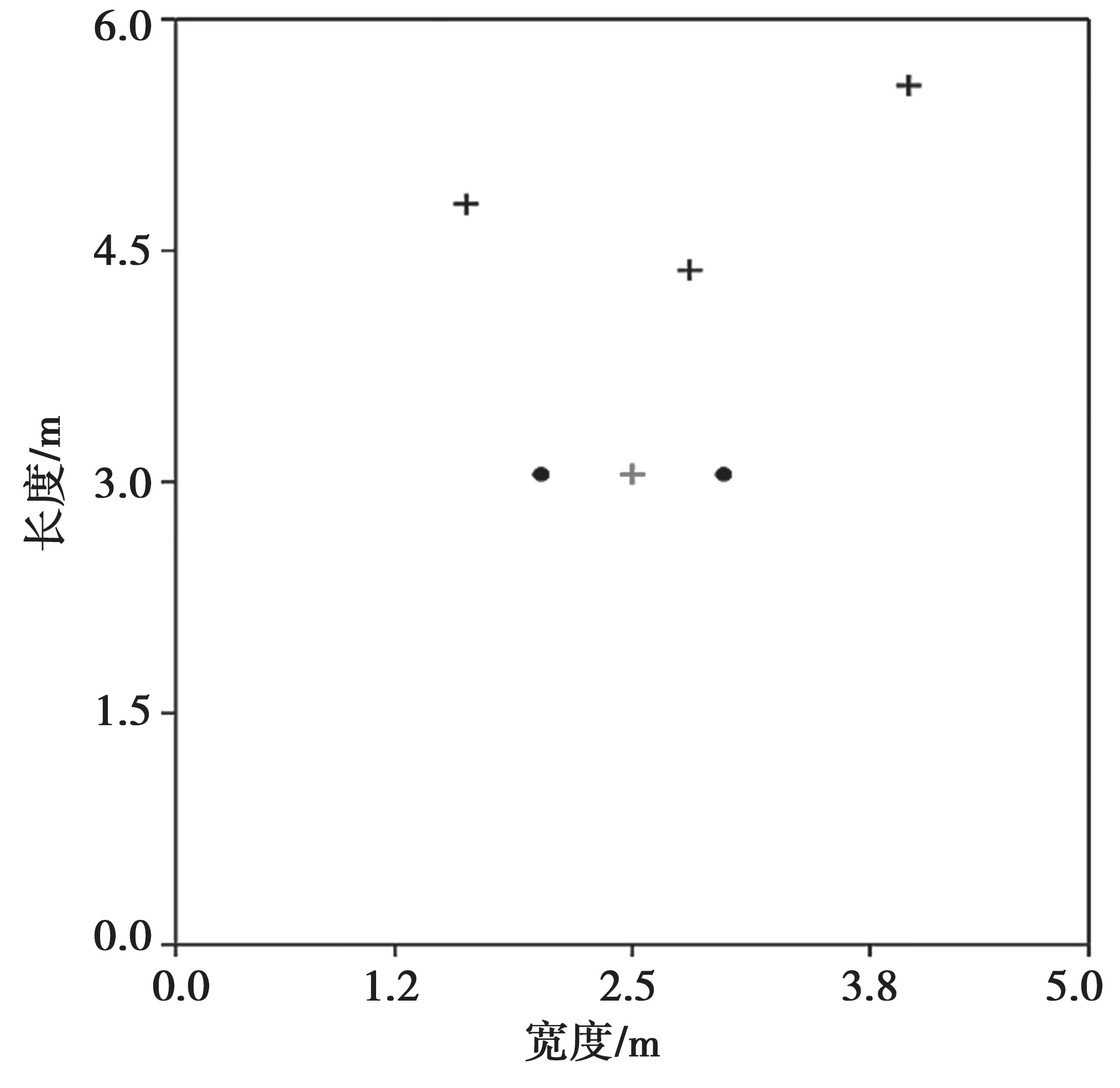
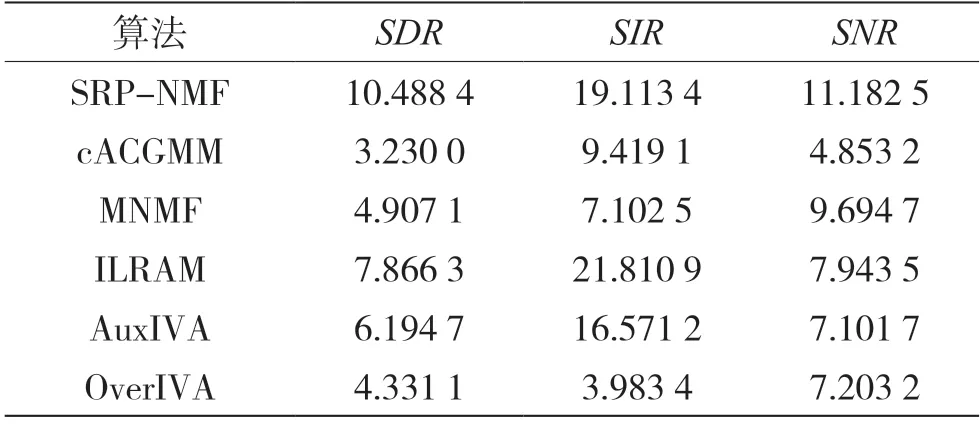
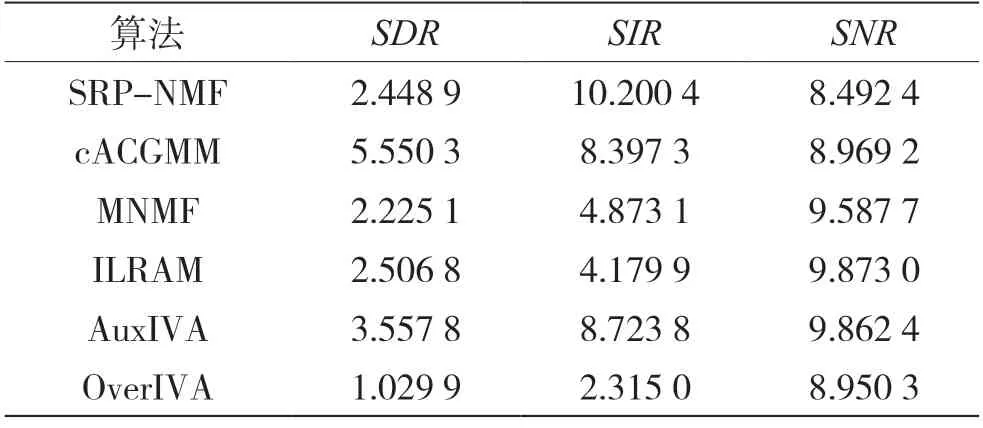
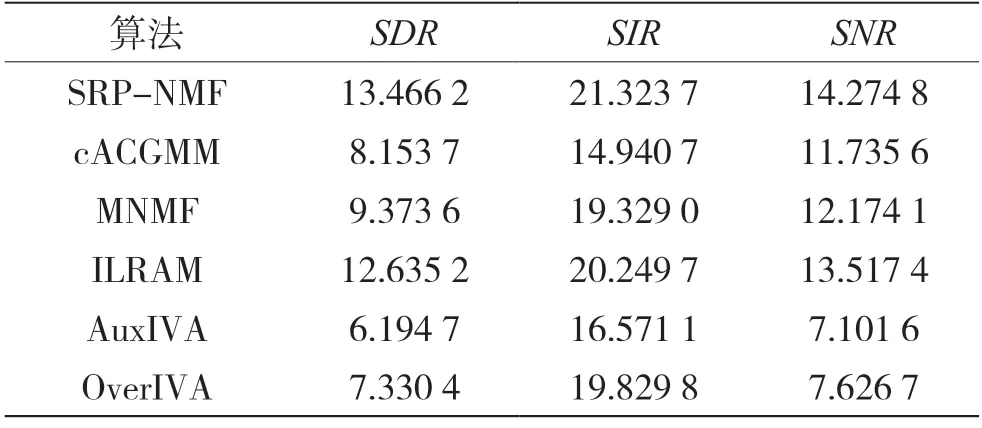
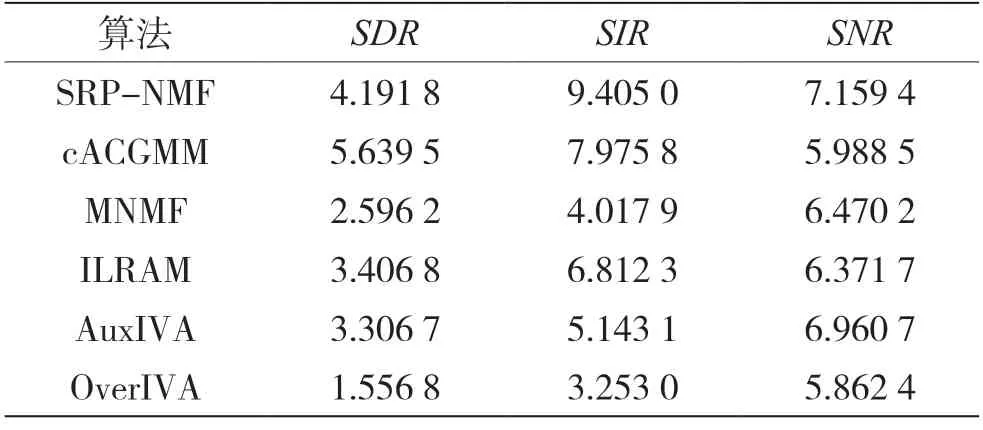
在正定(K=M)和超定(K 欠定(K>M)条件下的盲源分离算法主要是基于高斯混合模型(Gaussian Mixture Model,GMM)[5],这一类算法首先会通过聚类算法得到一个基于源信号的时频掩码,其次通过这个时频掩码对混合信号进行分离。 最近几年随着深度学习的快速发展,使用深度学习来解决盲源分离问题,成为了盲源分离研究的热点和重点,比如2016 年三菱电子研究实验室(Mitsubishi Electric Research Laboratories,MERL)提出了深度聚类[6](Deep Clustering,DPCL)。基于深度学习的盲源分离算法能够提高在高混响等复杂环境下的分离性能,但是这种方法也存在局限性:一是需要标准的数据集对神经网络模型进行训练,对设备性能要求高;二是大量基于深度学习的盲源分离算法需要知道一些先验知识,比如源信号的 数量。 非负矩阵分解[7](Non-negative Matrix Factorization,NMF)在多通道条件下的扩展引起了广泛关注。在2010 年,在欠定条件下将通道信息的空间特征和频谱特征结合起来,提出的多通道非负矩阵分解(Multilayer Non-negative Matrix Factorization,MNMF)[8],解决了欠定多通道盲源分离问题;随后为了解决正定和超定的盲源分离问题,在MNMF 的思想上进行改进提出独立低秩矩阵分析(Independent Low-Rank Matrix Analysis,ILRMA)[9]。 广义互相关-非负矩阵分解(Generalized Cross-Correlation-NMF,GCC-NMF)[10]也是结合空间特征和频谱特征的多通道盲源分离算法之一,通过结合广义互相关-相位转换(GCC-PHAse Transformation,GCC-PHAT)[11]源信号空间定位和NMF 算法,实现语音信号的分离。然而,GCC-NMF 算法只能解决双通道麦克风通道的情况,对于两个以上的情况则无能为力。而本文提出的可控功率响应-非负矩阵分解(Steering Response Power-NMF,SRPNMF)算法,受GCC-NMF 算法启发,结合可控功率响应和相位变换(SRP-PHAT)[11]源定位算法和NMF,对混合信号进行分离,并且SRP-NMF 可以适用于M≥2 的情况下的盲源分离。 由式(1)可知,xt是混合信号的时域表达形式,对混合信号进行短时傅里叶变换(Short-time Fourier Transform,STFT)可得: 式中,xft=[x1,ft,…,xM,ft]T为M维麦克风混合信号向量,Af=[amk,f]MK为源信号混合矩阵,sft=[s1,ft,…,sK,ft]T为K维的源信号向量,nft∈CM×1为高斯噪声。t和f分别是时间和频率的索引。M和K分别代表麦克风通道和源信号数量。 非负矩阵分解NMF 已成功地应用于单通道盲源分离问题中,主要思想是将非负矩阵Vft=|Xft|分解为基矩阵Wfd和权重矩阵Hdt两个非负矩阵,其中Xft是单通道混合信号。通过一定规则,迭代更新这两个矩阵,通过来估计Vft,其中d=1,2,…,D,D是基向量的数量。其中基矩阵Wfd的每一列称为一个基向量,表示为频率的非负函数。将每个时间点与相应的系数线性组合,来重建输入频谱图的相应列。 非负矩阵分解NMF 可以将矩阵分解问题转化成两个非负矩阵之间误差最小化的问题,本文使用IS 散度(Itakura-Saito divergence)[7]作为目标函数: 式中,⊙表示Hadamard 乘积,i表示迭代次数。对于多通道语音信号,将每个通道的Vm,ft=|Xm,ft|拼接成一个非负矩阵进行预处理,其中Xm,ft为第m条通道的混合信号,即: 然后通过NMF 对这个非负矩阵进行分解,根据式(4)和式(5)更新得到基矩阵Wfd和系数矩阵Hdt。因为每个麦克风通道的Wfd都一样,所以在分离过程中只需要对每个麦克风通道Hm,dt进行相应操作即可: 到达方向(Direction of Arrival,DOA)和到达时间差(Time Difference of Arrival,TDOA)[11]是在信号处理过程中常见的名词。DOA 是源信号相对麦克风的到达角度,TDOA 是表示不同通道之间信号的延迟程度。这两者都是一个相对的概念,在已知麦克风拓扑的结构下,两者可以相互转换。通过对DOA 和TDOA 进行估计,能够解决以下一些问题。 (1)如果只存在一个源信号,就可以通过DOA 对这个方向的信号进行增强。 (2)如果存在多个源信号,则: ①可以通过估计TDOA 的数量来对源信号数量进行估计; ②通过跟踪DOA/TDOA 的变化,来定位未知的源信号; ③通过对某一个特定的DOA 方向的源信号进行增强。 对DOA 和TDOA 的估计中,最简单的方法就是GCC-PHAT。GCC-PHAT 引入广义互相关的概念,通过最大化GCC 函数的延时估计TDOA。 式中,τ表示通道p和通道q之间的TDOA,定义为广义交叉谱[12](Generalized Cross-Spectrum)的离散傅里叶逆变换。 这种估计方法称为为GCC-PHAT。SRP-PHAT是在GCC-PHAT 的基础上进行改进而来,它使用相位变换[11]谱加权计算到达时间差来对多通道混合信号中的源信号进行定位。因为SRP-PHAT 可以通过两两麦克风组合之间的广义互相关来实现,因此可以表示为所有麦克风通道两两组合的GCCPHAT 之和的均值。如图1 所示,其中黑色表示的是在时间轴上的峰值,黑色不连续的地方表示该说话人没有说话,且同一时刻有多个峰值就表示有多个说话人进行说话,而这两条线对应的TDOA 就是源信号的最佳TDOA 索引。 图1 通过SRP-PHAT 算法得到的角谱 在本文中提出了一种新的多通道盲源分离的方法——SRP-NMF。受到GCC-NMF 算法的启发,通过将上面介绍SRP-PHAT 源定位算法和NMF 相结合,可以对混合信号进行分离。 图2 是SRP-NMF 的主要流程图,SRP-NMF 算法主要分为编码器、分离块和解码器。编码器和解码器都是一个两层结构,编码器包括STFT 变换和NMF 分解,而解码器包括一个STFT 逆变换和NMF逆分解。分离块主要分为SRP-PHAT 部分、部分和掩码生成部分。 图2 SRP-NMF 算法主要流程 式中,*表示共轭,Yft定义为FS[11](Filter and Sum)Beamformer 的输出功率: 式中,τm是第m个麦克风通道与参考麦克风通道的时间延迟,并且频域权重方程定义为: 根据NMF 分解出来的基矩阵Wfd本身是一个非负的频率函数这一事实,将Wfd与频域权重方程相结合,定义一组频率加权函数ψdft: 通过除以p、q个麦克风通道的信号幅值,归一化消除因信号幅值大小带来的影响。对于一个给定的基向量,根据它们频率的相对突出程度进行加权计算。结合式(9)~式(12),有: 图3 不同源信号的TDOA 对应的峰值 选取其中一个基向量,其中虚线表示不同源信号的τk。根据式(14),生成一个二进制掩码矩 阵。 式中,m是表示通道数。最后就是重构源信号,在解码器中将式(15)中得到的结果通过NMF 逆分解和短时傅里叶逆变换,得到相应的估计源信号。 式中,∠Xm,ft是混合信号的STFT 相位。 本文使用的数据集是WSJ0-2mix[13]和VCC[14]数据集,对这两个数据集进行空间化,通过执行RIR-Generator 工具包模拟一个房间将单通道信号转换成多通道信号。图4 为一个模拟房间平面情况,“·”代表麦克风,每个麦克风之间的距离为1 m,“+”表示源信号放置的位置,模拟麦克风数量2~8不等。数据集中混合信号的采样频率为8 kHz,数据集中混合语音信号的采样频率为8 kHz,STFT 使用窗口大小为512 样本点(64 ms)的hann 窗口,Hop 窗口大小为128 样本点(16 ms)。默认的NMF 参数设置基向量数量D为128,迭代次数为100 次。 图4 模拟房间的平面示意 本文主要使用了一个开源工具包BSS Eval[15]来量化分离性能。由于在原始的BSS Eval 中,这个工具包只适合评估单通道语音信号,在这基础上进行修改,修改后可以对多通道信号的分离结果进行评估。实验中主要使用的BSS Eval 评估标准指标为信号失真比(Signal-to-Distortion Ratio,SDR)、信号干扰比(Signal-to-Interference Ratio,SIR)以及人造误差成分(Sources-to-Artifacts Ratio,SAR)。 cACGMM[16]算法是基于高斯混合模型(Gaussian Mixed Model,GMM)的一种多通道算法,使用复杂的角中心高斯分布作为其类条件分布,这个模型只使用通道内的相位差异,而不是用绝对相位。MNMF是扩展到多通道的NMF 算法,而ILRAM 是通过在源信号估计中引入NMF 来扩展IVA 得到该算法。基于扩展独立向量分析(Independent Vector Analysis,IVA)算法的还有AuxIVA 和OverIVA[17]。以上的多通道盲源分离算法,有些算法只适应于正定的情况,而有些算法却只能解决超定和正定这两种情况。比如ILRAM 和AuxIVA 算法就只适用于正定的情况。但是SRP-NMF 除了解决正定和超定条件下的盲源分离问题,也能解决更复杂的欠定多通道盲源分离问题。 在表1 和表2 中,分别得到了两组在不同情况下,各个算法在多通道混合语音分离中的实验结果评估指标SDR、SIR和SAR。 在表1 和表3 中,清楚地看到,在两个数据集中,SRP-NMF 算法的总体评估结果明显优于其他的多通道算法。在表2 和表4 中,对于高混响的情况下,尽管SRP-NMF 算法的分离效果提升不是那么明显,但是相对于其他算法来说,整体水平优于其他算法。综合这4 个表中的实验评估数据,SRP-NMF 算法在整体水平上都显著地提高。 表1 在WSJ0-2mix 数据集中,由BSS Eval 得到的平均SDR、SIR 和SAR(RT60=70 ms) 表2 在WSJ0-2mix 数据集中,由BSS Eval 得到的平均SDR、SIR 和SAR(RT60=370 ms) 表3 在VCC 数据集中,由BSS Eval 得到的平均SDR、SIR 和SAR(RT60=70 ms) 表4 在VCC 数据集中,由BSS Eval 得到的平均SDR、SIR 和SAR(RT60=370 ms) 本文提出了一种将通道的空间特征与NMF 相结合的无监督语音分离方法。SRP-NMF 算法利用SRP-PHAT 源定位算法计算每个源信号的TDOA,与NMF 中分解出的基矩阵结合起来,将它们分组到对应源信号中,并生成一个系数掩码,通过这个掩码对混合信号进行分离。 实验表明,SRP-NMF 算法优于其他的多通道盲源算法。在混响环境下,无论有无噪声混合,SRP-NMF 算法都能准确有效地分离混合语音,分离效果比其他算法有显著提升。而且本文提出的SRP-NMF 算法对于多通道盲源分离问题,适用性强,能够解决正定、超定和欠定条件下的多通道盲源分离问题。1 相关工作
1.1 多通道混合语音

1.2 NMF


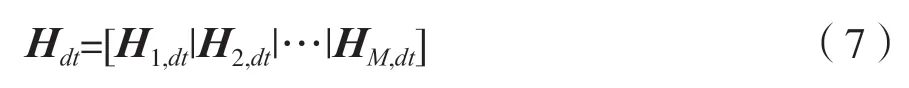
1.3 DOA 和TDOA
1.4 SRP-PHAT

2 SRP-NMF

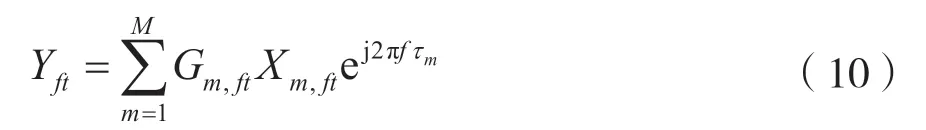

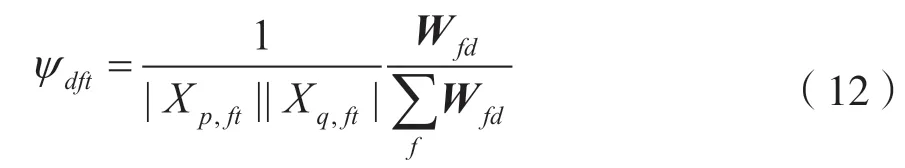
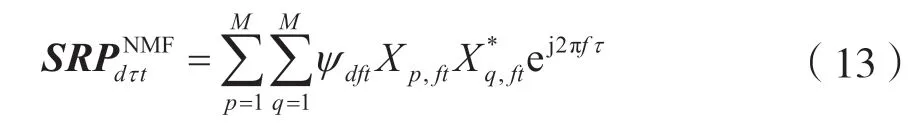

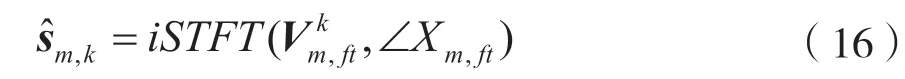
3 实 验
3.1 数据集
3.2 评价指标
3.3 评价结果
4 结语

