模块化多电平换流器非线性控制策略*

徐晓瑜，陈 焰，涂志波，孙 玲，王 方

（1.昆明理工大学，云南 昆明 650500；2.玉溪师范学院，云南 玉溪 653100）

0 引言

作为一种新型电压源型换流器，模块化多电平换流器（Modular Multilevel Converter，MMC）具备谐波特性好、可独立控制有功无功以及易于扩展等优点，在柔性直流输电领域得到了广泛关注，有着广阔的应用前景。

目前，国内外关于MMC 的研究主要针对MMC的拓扑及其仿真、控制与调制策略、换流器产生的子模块均压问题、环流抑制等方面。文献[1]中分析了MMC-HVDC 系统的拓扑结构，详细推导了dq坐标轴下的MMC 数学模型，并给出了双闭环控制策略。文献[2]给出了MMC 欧拉-拉格朗日模型，详细论证了MMC 的无源性，并给出了MMC 无源控制系统的设计。文献[3]介绍了载波移相调制（Carrier Phase Shift-Sinusoidal Pulse Width Modulation，CPSSPWM）和最近电平逼近（Nearest Level Modulation，NLM）两种调制策略，分析了相应调制方式下的子模块均压策略，对3 种调制技术进行了对比。实验结果表明，载波移相调制开关频率更低，损耗更小，输出谐波以高次谐波为主，谐波总畸变率更低。文献[4]研究了载波移相调制下移相角与输出电平数的关系，除了传统的N+1 电平输出电压，改变相移角度还可实现MMC 的2N+1 电平输出，使得换流器的性能发生变化。文中具体分析了两种调制方式的规律，并给出了相应的实现方法。文献[5]分析了移相角与输出电压谐波的变化规律，其中移相角可改变输出的电平数而不增加器件数量。相间环流是影响换流器传输性能的一个关键问题。文献[6]提出一种环流抑制器。与以往需要坐标系变换和各相解耦不同，该控制策略独立抑制每相环流中的二倍频分量，适用于其他单相或四线制系统，实现更简便。

本文的主要内容将围绕MMC 的拓扑及原理、系统级非线性控制策略、调制策略和环流抑制4 方面展开，并利用Matlab 进一步对比了N+1 和2N+1电平下换流器性能。仿真结果表明，所提控制策略具有可行性。

1 MMC 拓扑结构及数学模型

1.1 MMC 拓扑结构

为了研究MMC-HVDC 系统控制策略，先分析MMC 拓扑特点及其数学模型。典型N+1 电平的MMC 拓扑简化电路如图1 所示。每相包含上下两个桥臂，每个桥臂有N个子模块（Sub-Module，SM）级联。子模块一般采用半桥结构。

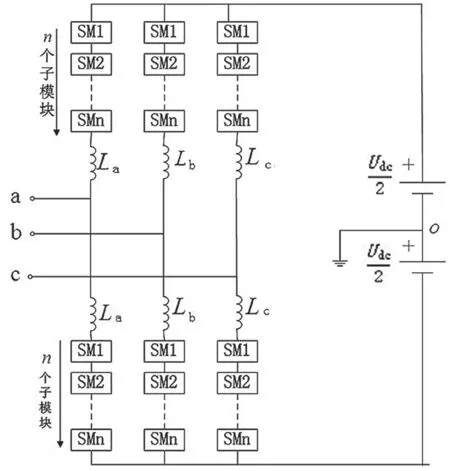
图1 MMC 拓扑简化电路

1.2 MMC 数学模型

MMC 各相结构对称，等效电路如图2 所示。

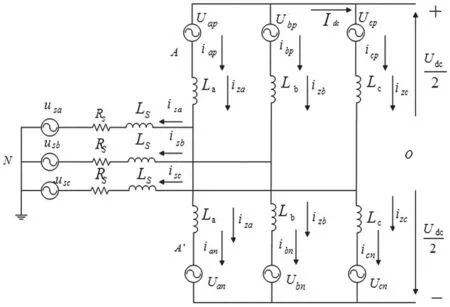
图2 MMC 等效电路

三相静止坐标系下MMC 的数学模型为：

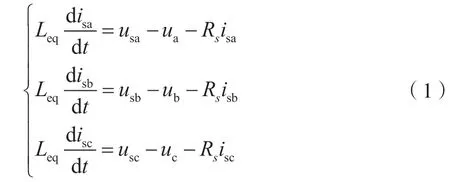
通过分析上述模型，发现三相abc 静止坐标系下各物理量都是随时间交变的，不利于传统的系统级控制和有功功率、无功功率的独立调节。因此，该模型需经过变换到两相坐标系中。

从三相abc 静止坐标系到两相αβ静止坐标系的变换称为Clark 变换，变换矩阵记为C3s/2s。从两相αβ静止坐标系到两相任意旋转dq坐标系的变换为Park 变换，变换矩阵记为C3s/2r。最终，可得从abc坐标系到dq坐标系的3s/2r变换关系为：

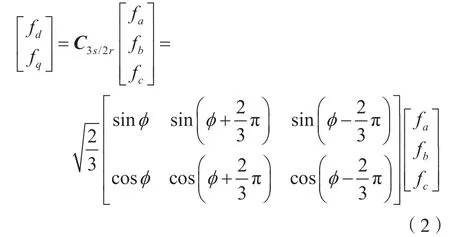
用C3s/2r矩阵左乘式（1）表示出的矩阵模型，可得：

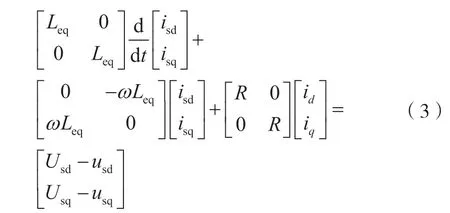
将式（3）展开，有：

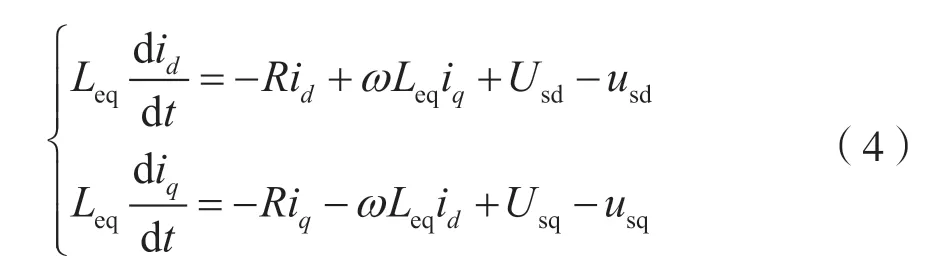
式（4）就是MMC 换流器在dq旋转坐标系下的解析模型。

2 MMC-HVDC 系统控制策略

2.1 系统的控制流程

MMC-HVDC 控制系统结构，如图3 所示。系统级控制的主要目的是达到给定，通过对设定值的计算产生下一级控制器所需的参考值。这一层在传统双闭环控制中由外环完成。换流站级控制主要接收上一级输出的参考量，经过调节产生下级需要的调制波，由内环完成。换流阀级控制在所给调制波上叠加均压、环流抑制产生的压降分量，再使用适当的调制策略产生开关器件所需的脉冲触发信号。

图3 MMC-HVDC 控制系统结构

本文中采用直接电流控制，也称矢量控制。通过直接对输出电流指令信号进行处理，引入直接电流的反馈控制回路，可以实现对电流瞬时值的快速跟踪，控制精确、稳态特性好且响应迅速。系统的控制框图见图4。外环输入有功物理量和无功物理量，经过锁相、PI 调节分别生成d轴和q轴电流参考值作为内环电流给定。内环采用无源控制器，计算参考值与实际值的误差，经过解耦控制、坐标变换得到三相静止坐标系下的调制波。阀控制的核心调制策略用载波移相调制策略。

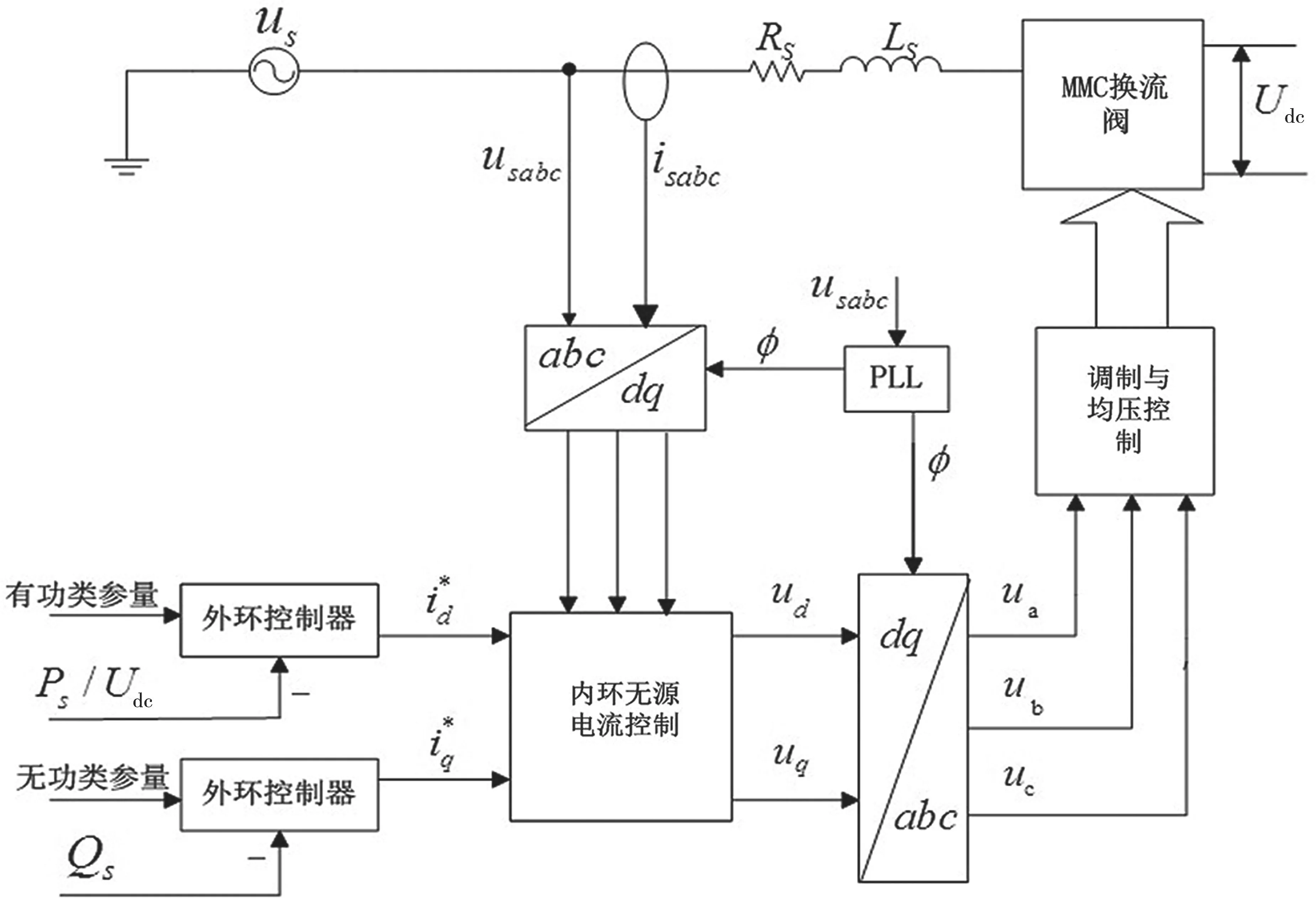
图4 系统的控制原理

2.2 基于无源控制的内环控制器

MMC 的控制性能与电流内环控制器的设计关系紧密。由MMC 数学模型的分析可知，MMCHVDC 系统是一个多变量、强耦合的非线性系统。一般线性系统的控制方法很难达到控制要求。

无源控制以其能够实现系统的全局稳定性、对外界扰动和参数的变化具有较强的鲁棒性等特点，成为研究非线性系统的有效方法。

（1）MMC 的欧拉-拉格朗日（Euler-Lagrange，EL）系统模型

根据非线性无源控制理论，可以将式（3）改写为：

（2）MMC 的无源性

定义正定函数Q(x)、正定能量存储函数V(x)，系统的输入、输出分别记为u、y，能量供给率为uTy。

对于一个多输入多输出系统，若存在V(x)、Q(x)，对∀T>0 使得耗散不等式：

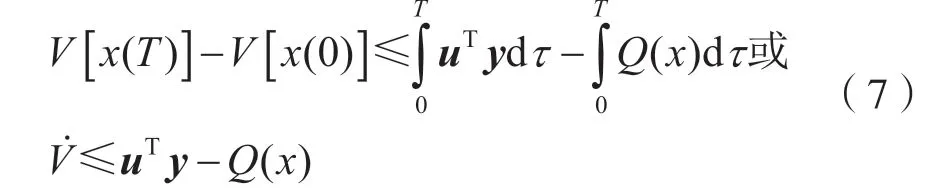
式（7）对u、y、uTy均成立，则系统是严格无源的。

对于三相MMC，设系统的能量存储函数为：

对V求导，由式（5）可得：

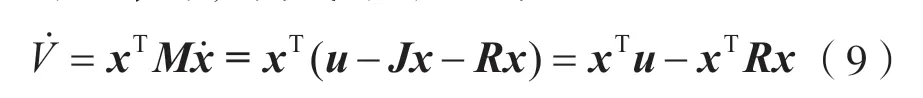
（3）MMC 无源控制器设计

MMC 系统稳态运行的目标是有功功率、无功功率和交流电压跟随相应的给定值，因此系统期望的稳定平衡点为：

建立误差系统，令：

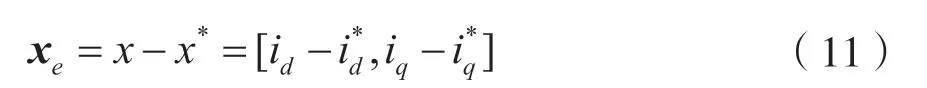
式中，x*为系统期望平衡点。

将式（11）代入式（6），可得系统误差动力学方程为：

向系统注入合适的阻尼，能加速系统额外能量的耗散，以此保证系统快速收敛到给定状态，使Verr调节到0。

注入阻尼的耗散项为：

式中：Rd为系统阻尼矩阵；Ra为待注入的阻尼矩阵，为正定矩阵，其中Ra1＞0、Ra2＞0。

将式（14）代入式（13），重新列写得到注入阻尼的误差方程为：

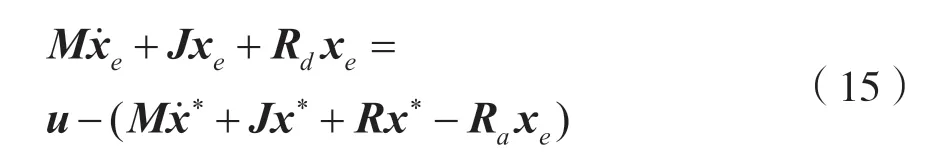
为消除稳态误差，实现解耦控制，选无源控制规律为：

则MMC 无源控制器表达式为：

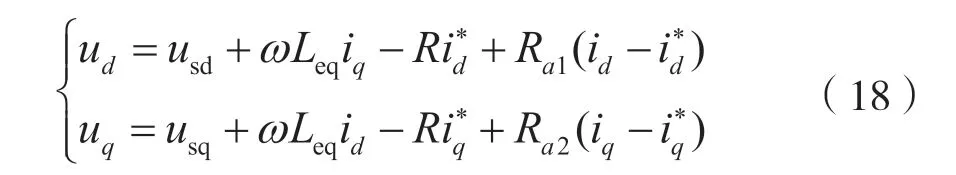
MMC 无源控制器的控制框图如图5 所示。

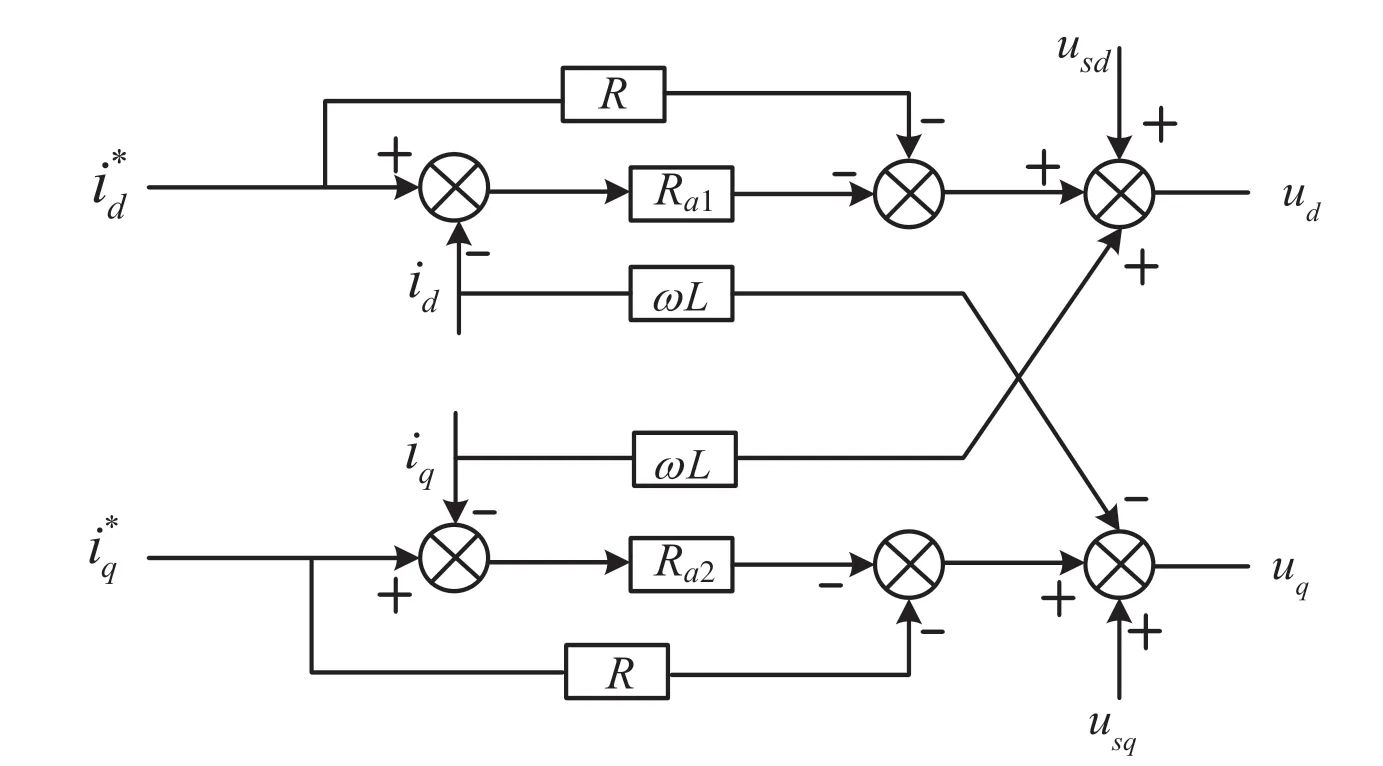
图5 MMC 无源控制器

采用无源控制，注入阻尼的参数大小Ra1、Ra2是影响MMC 控制性能的关键，因此综合控制效果和对换流器的影响，本文选取Ra1=Ra2=100 Ω。

2.3 MMC 调制策略研究

（1）常用的是最近电平逼近（NLM）和载波移相脉宽（CPS-SPWM）两种调制策略。本文使用的仿真模型SM 数为1～10，因此重点研究载波移相调制技术。

（2）子模块电容电压的均衡是换流器稳定运行的关键环节。由于本章侧重研究载波移相调制策略对换流器的影响，因此简化仿真条件，假定每个桥臂的子模块直流电压已经达到期望值。

在载波移相调制（CPS-SPWM）技术中，由于移相角的不同，决定了某时刻上下桥臂投入的子模块数不同，因而输出电平数也发生了变化。定义移相角θ为下桥臂子模块载波相对上桥臂的延迟角，则可总结出以下规律：

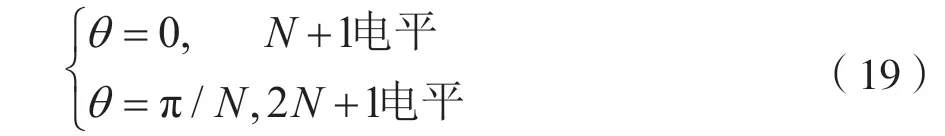
2.4 环流抑制策略

三相MMC 装置在实际运行时，由于子模块电容反复的充放电，其电压不会时刻保持均衡，因此产生环流抑制，所以加以抑制。本系统采用准比例谐振（Quasi Proportional Resonance，QPR）控制器。

准比例谐振抑制器的传递函数为：

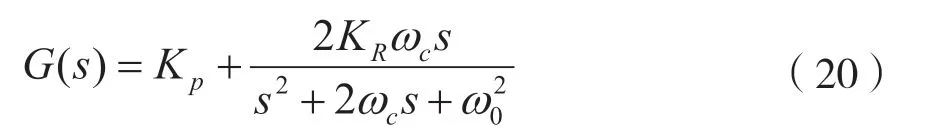
式中，Kp为控制器的比例系数，KR为谐振系数，ω0谐振频率，ωc截止频率。根据式（20）设计QPR 控制器的控制框图，如图6 所示。

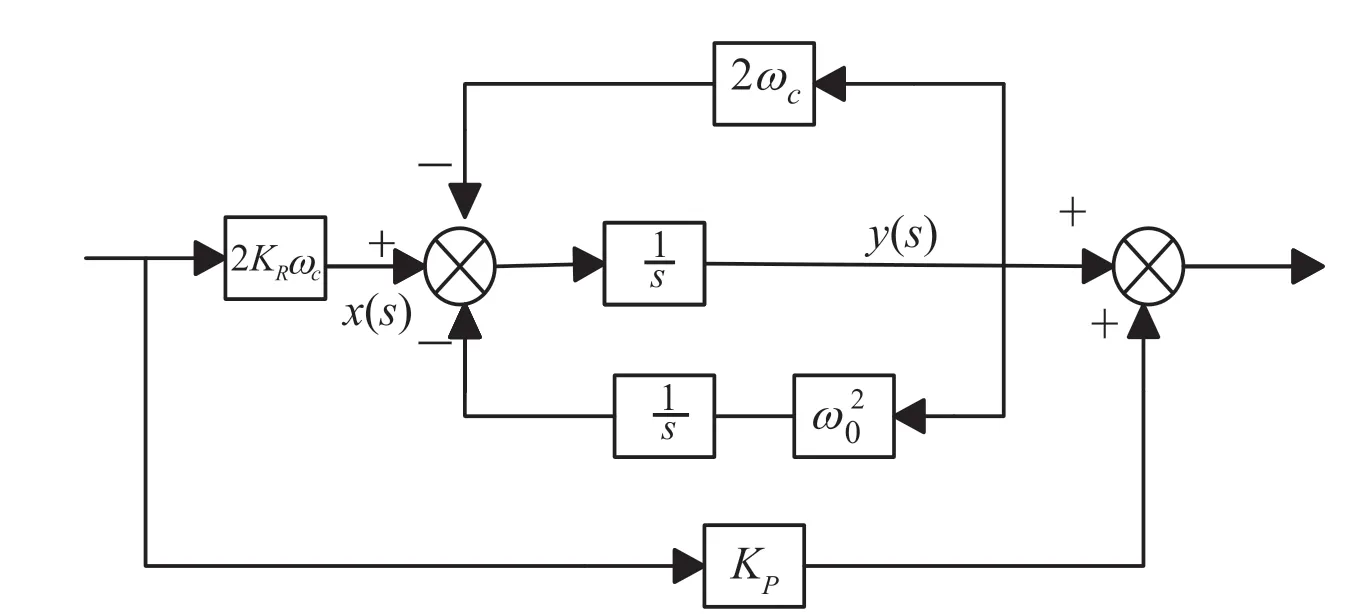
图6 准PR 控制器实现

3 总体仿真及对比分析

前面分模块介绍了MMC 的控制系统和环流抑制机制，为了比较传统N+1 电平和改进2N+1 电平调制方法的差异，验证无源控制理论的可行性，在Matlab/Simulink 中搭建三相4SM 并网逆变模型。外环图7 是MMC 主电路，仿真参数如表1 所示。

表1 三相MMC 并网仿真参数

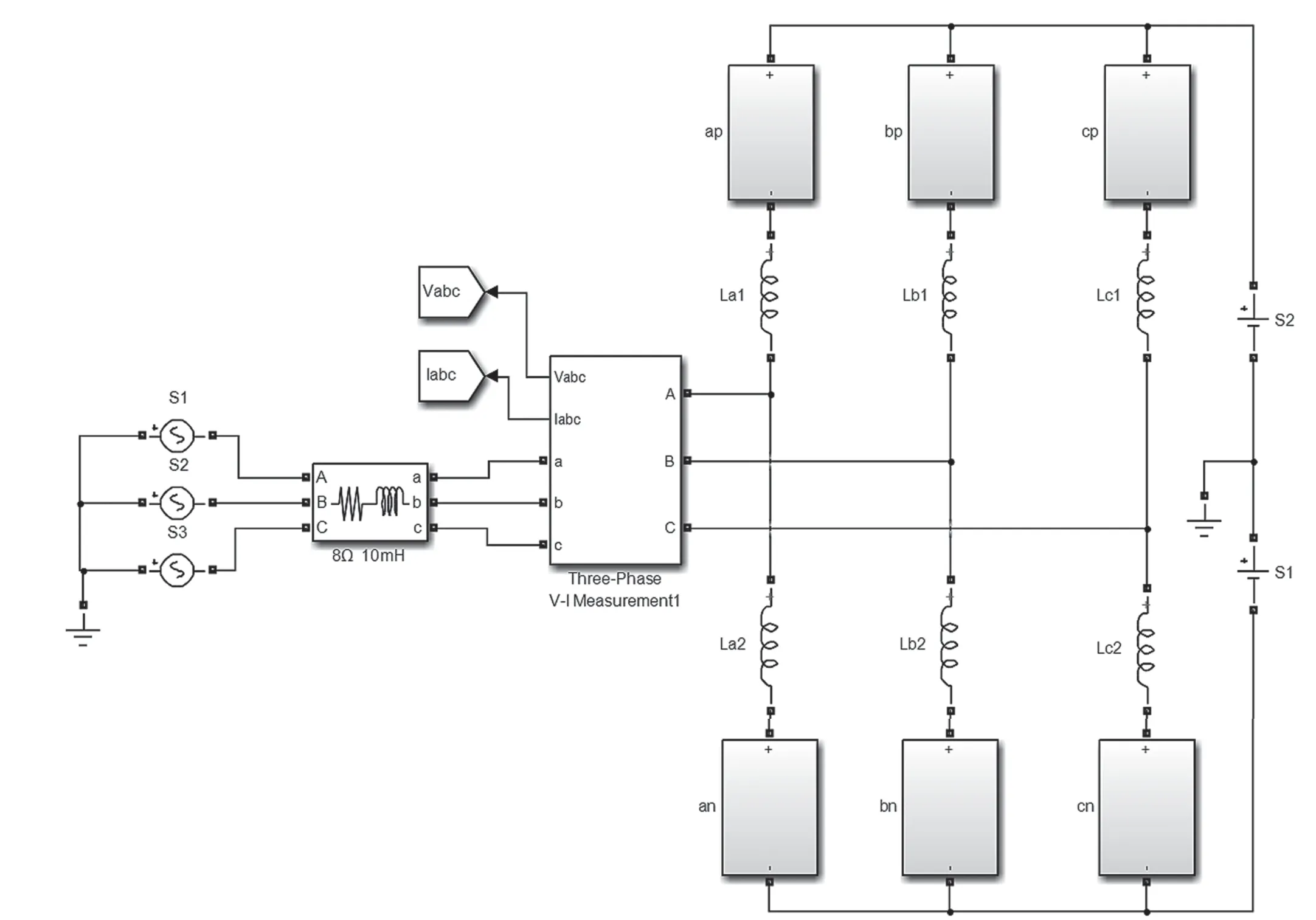
图7 三相并网MMC 逆变电路

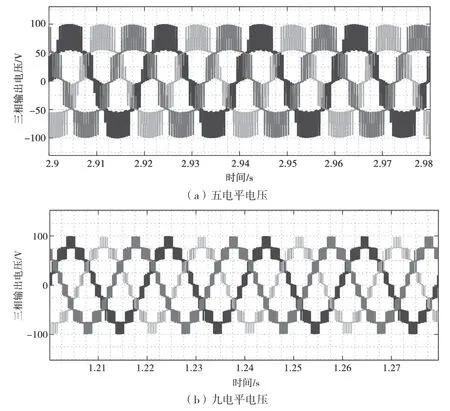
图8 输出三相电压

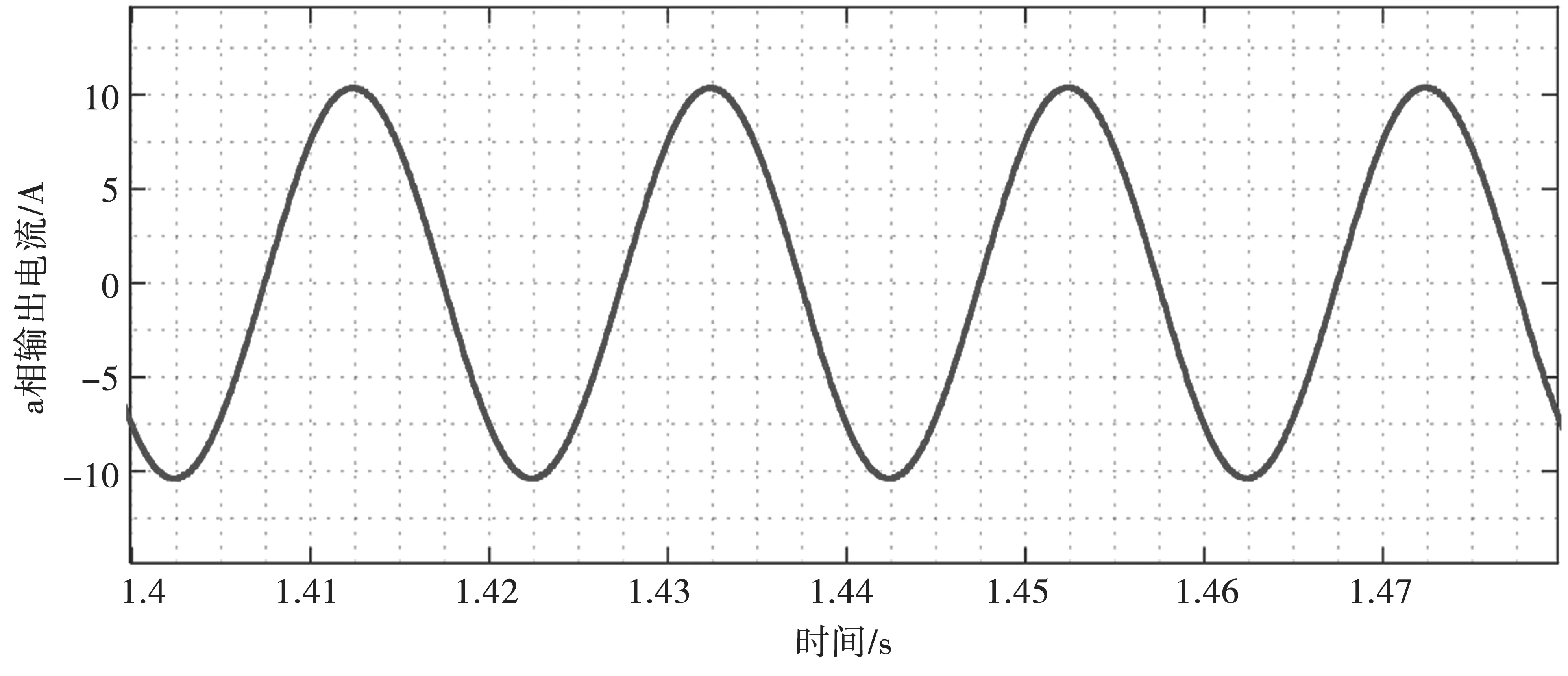
图9 输出三相电流

以a 相为例，图8（a）、图8（b）是五电平和九电平输出电压波形。环流抑制前后，五电平输出电压THD由30.23＆降至26.49＆，桥臂电流THD由31.85＆降低至6.18＆；九电平输出电压THD基本保持在14.7＆，桥臂电流THD由31.04＆降低至9.70＆。图9 为一相输出电流波形，两种电平数下的输出电流正弦度均很高，九电平的波形杂波成分更少。图10 为环流抑制效果，两方法均能在投入环流抑制器后0.5 s 内实现抑制，证实了环流抑制策略的快速性。对比图10（a）和图10（b），由于九电平模型桥臂电流畸变更加严重，抑制之后环流中的杂波成分仍较多，因而五电平的抑制效果更显著。

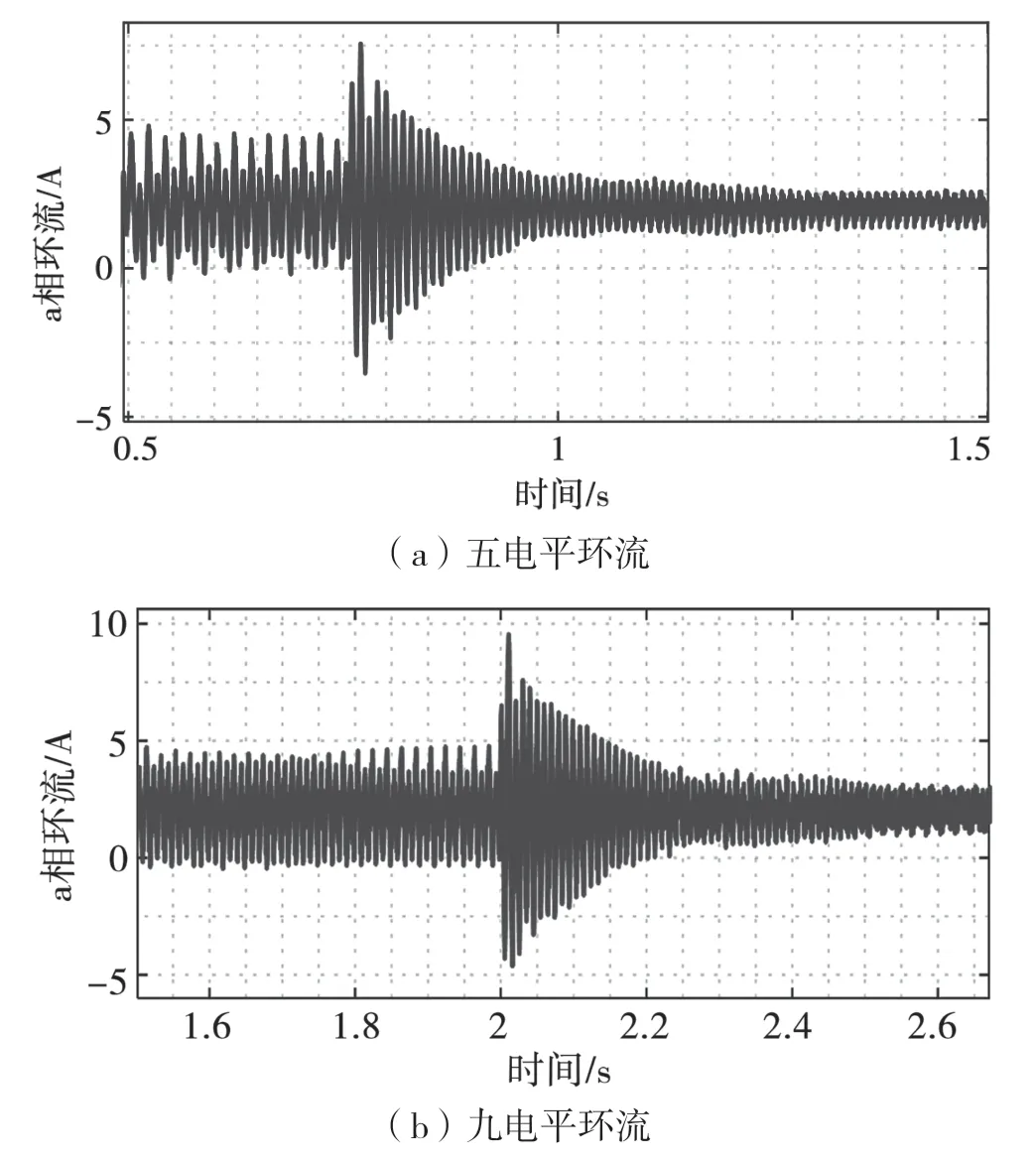
图10 环流抑制效果

从整体仿真效果来看，加入无源控制器实现了对阀级以上系统的有效控制，一方面能快速调节好环流，减小环流抑制器投入瞬间大幅波动，另一方面使稳态误差维持在较小范围内，促使换流器达到期望的功率传输。

4 结语

通过围绕MMC 的拓扑及原理、系统级非线性控制策略、调制策略和环流抑制4 方面展开分析，利用Matlab 进一步对比了N+1 和2N+1 电平下换流器性能，验证了所提控制策略的可行性。