基于多相滤波的软件无线电接收机*

赵文超，黄 伟，李 翔，侯改利

（武汉中原电子集团有限公司-研发中心，湖北 武汉 430205）

0 引言

软件无线电的思想是尽可能简化射频前端，使ADC 尽可能靠近天线。直接射频采样软件无线电结构最符合这一要求。目前，软件无线电接收机基本采用低通滤波或者高效数字滤波器（如积分梳状滤波器、半带滤波器）来实现。这种结构一般工作在较低的中频，信号带宽较窄，在宽工作频带时无法满足直接射频采样软件无线电结构要求。这是因为低通滤波具有良好的通带和阻带特性，但对运算处理要求较高，在高速数据流的情况下难以满足实时性要求。高效数字滤波器虽然能够一定程度简化和降低运算处理要求，但依然难以满足高实时性要求，同时会对宽带信号频谱造成一定的失真。

直接射频采样需要对整个工作频段的信号进行采样。假设fmax为工作最高频段，根据Nyquist 采样定理[1]，采样速率fs应满足：

比如工作频段30～512 MHz，按照Nyquist 定理采样率fs至少1 024 MHz。如此高的数据速率对于目前主要的信号处理芯片FPGA 和DSP 来说，无论采用低通滤波还是高效数字滤波都很难满足实时性要求，且无法保证稳定性。

多相滤波技术可以克服以上滤波器的缺点，通过将单路高速数据流分解成D路数据并行处理，从而使每路子滤波器运算速度要求降为fs/D，从而提高接收机实时性和稳定性，同时保留低通滤波器良好的通带和阻带特性，满足宽带信号频谱处理要求。多相滤波还有一个固有好处，即由于滤波器系数被分解成了多个子滤波器系数，因此子滤波器的累积误差会减少，从而提高了数据精度。

本文基于多项滤波技术提出了基于多相滤波的软件无线电接收机模型，非常适用于直接射频采样软件无线电结构，有效解决了直接射频采样时软件无线电接收机面临的数据运算能力不足和实时性无法保证的问题，同时保留了基于低通滤波的软件无线电接收机优点。算法分析和仿真结果表明，该结构具备实时性强、稳定性好及运算精度高的特点。

文章第1 部分介绍了软件无线电接收机原理，给出了基于多相滤波的软件无线电接收机模型。第2 部分介绍了整数倍抽取理论，是软件无线电接收机理论基础。第3 部分介绍多相滤波技术，给出了多相滤波抽取结构。第4 部分给出抽取多项滤波FPGA 实现结构，通过计算和仿真说明了该结构具备的优势。第5 部分进行了总结。

1 软件无线电接收机原理及结构

根据Nyquist 采样定理，高频模拟信号经过数字ADC 采样后，在数字域形成一定的频谱结构，采样后的数字信号表示为XD(f)。接收机的主要目的是从XD(f)中提取出感兴趣的基带信号s(n)。由于任何一种调制信号都可以用幅度、相位和载波对应的函数来表示，所以信号s(n)可表示为：

式中，A(n)、ω0、θ(n)分别为信号的幅度分量、载波分量和相位分量。对式（2）进行三角函数正交分解，得到s(n)的正交表达形式为：

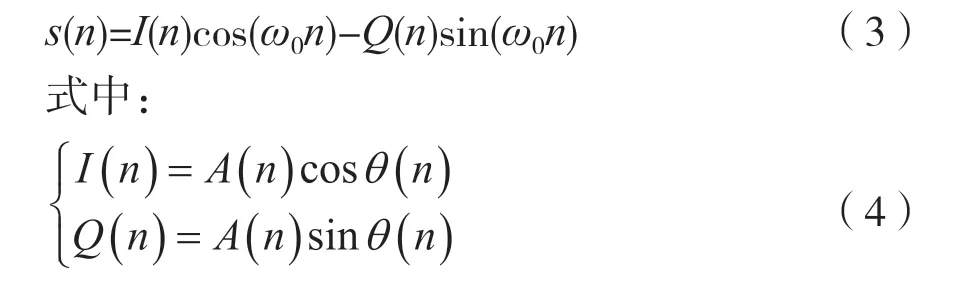
式（3）称为基带信号的两个正交分量，即同向分量和正交分量[1]。载频ω0主要用于信号频谱搬移，不携带信息，所以调制信号s(n)完全可以由两个正交分量来表征。接收机的主要作用是从载波处提取这两个正交分量，在频谱不失真的前提下进行数据流降速处理后输出给后续解调模块。如图1所示，混频器产生正交的两路信号，低通滤波器Hi(ejω)主要滤除I(n)和Q(n)频谱分量以外不需要的信号，以消除邻道干扰的影响。经过接收机提取后的正交分量信号I(n)和Q(n)已经变为基带信号，假设其带宽为B，由于B≤fs/2，因此可以对正交分量I(n)和Q(n)进行抽取。设抽取值为D，则D可表示为：

满足式（5）关系的信号抽取不会改变原频谱结构，信号不会失真。抽取后的信号可以表征原始信号，但数据速率降低为之前的1/D，大大减轻了后续基带处理模块的数据处理能力要求。例如，fs=200 MHz，B=25 kHz，则根据式（5）可得D=2 000。这样在对相同信号进行处理时，基带处理模块的数据处理速度可以降低2 000 倍。基于低通滤波的软件无线电接收机如图1 所示[2]。低通滤波器和后接的各级抽取器构成了一个标准的抽取系统，用于降低后续处理模块速率的处理要求。

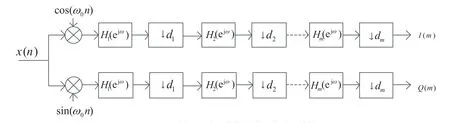
图1 基于低通滤波的软件无线电接收机结构

图1 共采用了M级抽取，每一级的抽取因子分别为Dm，总的抽取因子为：

该结构可以有效降低后级处理模块运算速度要求，但由于滤波器数据输入端处在抽取器之前，滤波器需要提供高速运算能力，特别是在高速取样率情况下，前级滤波器将面临很大的数据处理压力，对处理器是一个大的挑战，不利于实时性和稳定性要求高的系统。由图1 可知，滤波器输入速率最高处在第一级，也就是前级需要提供较高的数据运算能力。

针对软件无线电接收机前级速率要求高的特点，本文提出了一种改进的接收机结构，即基于多相滤波的软件无线电接收机结构，如图2 所示。这种结构将前级滤波器改用多相滤波结构来实现。多相滤波器运用子滤波器并行运算的特点，在满足总的运算速度要求前提下，可以降低子滤波器速率要求，从而在高速取样率情况下有效取代低通滤波器，解决硬件运算能力不足的问题，有效提高接收机的实时处理能力，同时提升硬件运行稳定性。

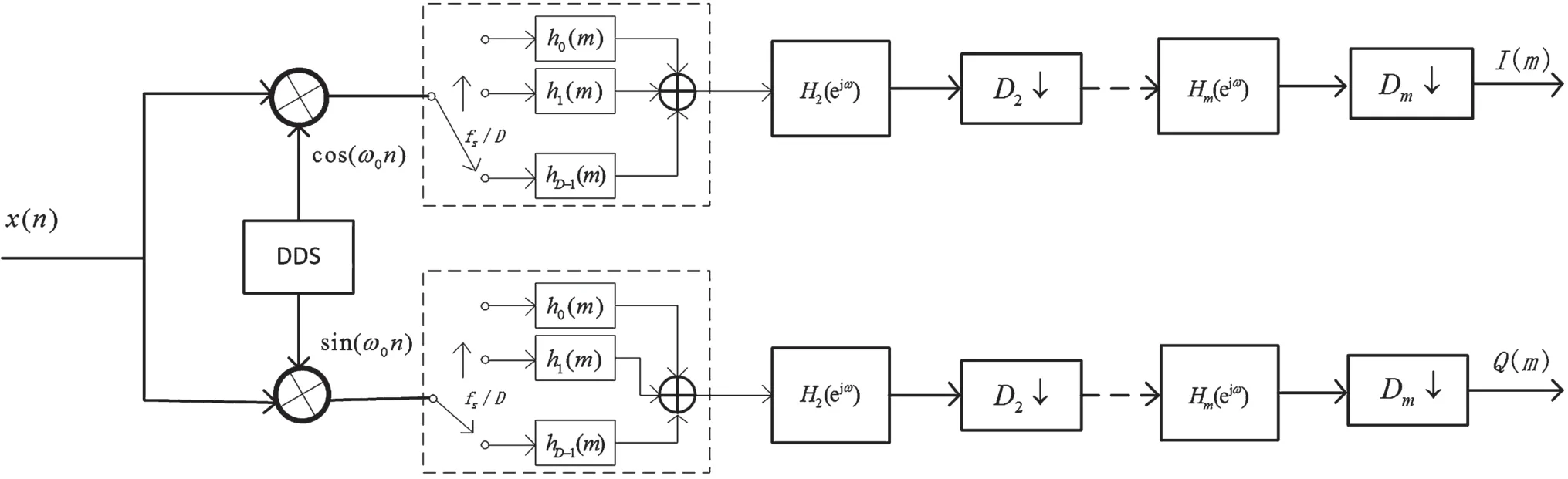
图2 基于多相滤波的软件无线电接收机结构

2 低通整数倍抽取

软件无线电接收机结构中低通抽取器的主要作用是对基带正交信号数据流进行降速，且不改变信号频谱结构，目的是降低后续基带处理模块数据处理要求。多速率信号处理整数倍抽取是其基本理论基础，因此深入理解和掌握整数倍抽取理论对软件无线电各种接收机结构都至关重要[2]。

整数倍抽取是将高速采样序列x(n)每间隔D-1 个数据选取一个样点，得到一个新低速序列xD(m)，即：

抽取序列的离散傅里叶变换为[3]：

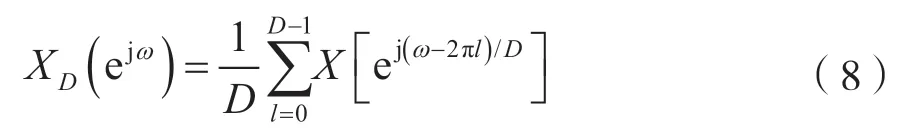
由式（8）可知，抽取后的低速序列频谱XD(ejω)为原高速序列频谱X(ejω)经过2π周期频移和D倍频谱拓展后叠加而成。由图3 可知，在频谱频移和拓展的过程中频谱会发生混叠，这时需要先对原始高速序列频谱进行滤波，滤除带宽π/2（D=2）以外的信号，然后进行2 倍抽取，使得抽取后的低速序列不会发生频谱混叠，且可以准确表征原高速序列感兴趣频谱部分。

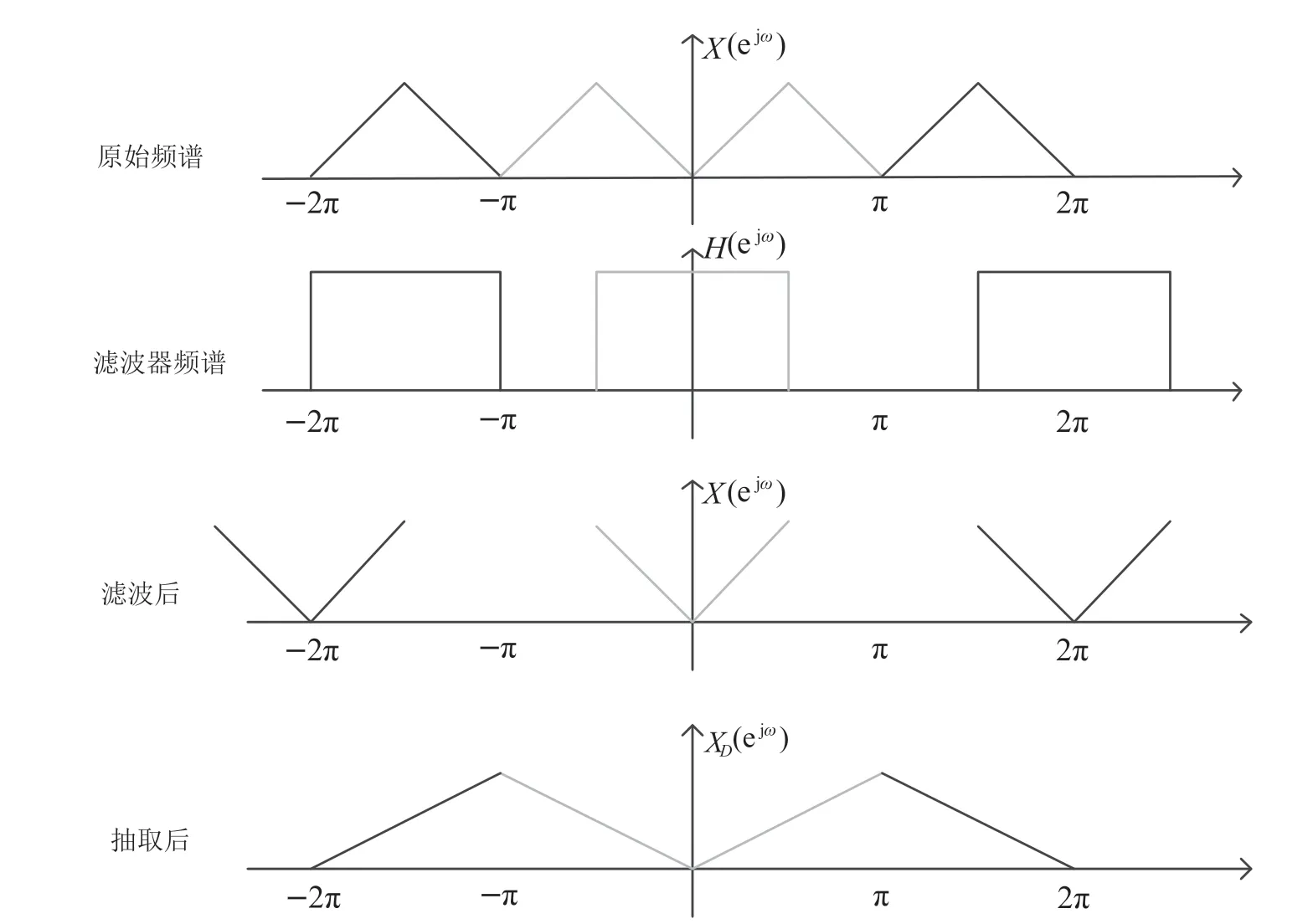
图3 抽取（D=2）后的频谱结构

这样抽取后的低速序列频谱XD(ejω)可以准确表示原高速序列频谱X(ejω)，后续基带处理模块只需提供较低的数据处理能力，就可完成对原始信号的等同处理。它的数据速率只需高速序列时的1/D，大大降低了对后续基带处理模块处理速度的要求。

图4 为标准的低通抽取结构，可以降低基带速率同时防止频谱混叠，是软件无线电接收机的重要组成部分。

图4 低通整数倍抽取器结构

3 多相滤波器原理及抽取结构

低通整倍抽取结构的主要缺点是对运算速度的要求太高。这是因为低通滤波器在抽取前，高速数据先经过低通滤波器后再进行抽取，这样低通滤波器需要工作在高速数据流下，特别是在高速采样情况下，将会面临更大的数据处理能力挑战。该结构对实时要求高的系统非常不利，甚至可能无法满足运算速度要求。为了提高系统实时处理能力，下面介绍多相滤波抽取结构[2,5]。

冲击响应为h(n)的数字滤波器，其z变换H(z)定义为[3]：

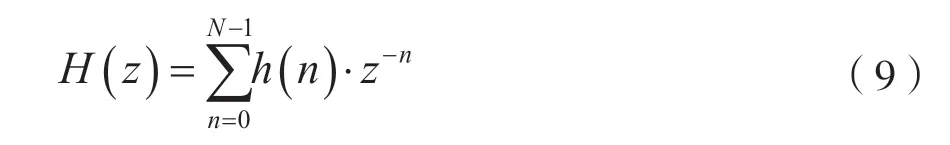
令n=mD+k，其中m=0,1,2,…,M-1，k=0,1,2,…,D-1，N=M·D，则式（9）可改写为如下形式：

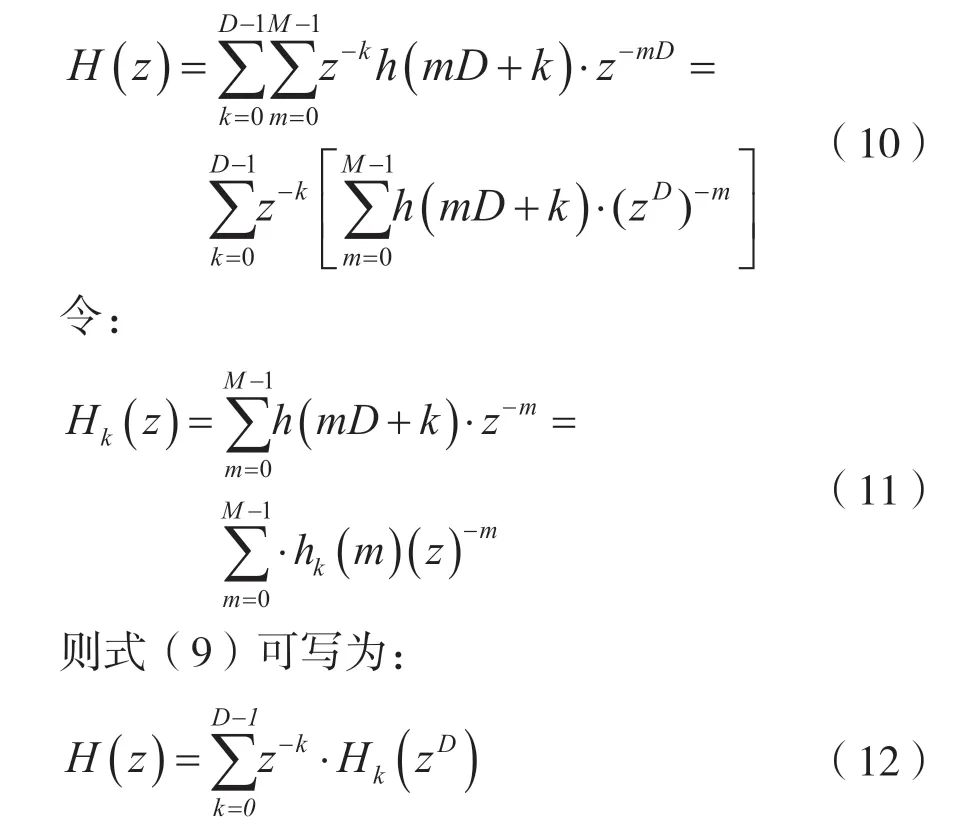
式（12）为数字滤波器H(z)的多相滤波结构，如图5（a）所示。根据Noble 恒等式[4,6]，D倍抽取和多相滤波的延时单元进行合并，得到多相滤波抽取结构，如图5（b）所示。

图5 多相滤波抽取结构

由图5（b）可知，多相滤波器的子滤波器位于D倍抽取后，即数据是经过降速后再进行滤波器处理的，大大降低了滤波器数据处理要求，提高了滤波器的实时处理能力。另外，由于原低通滤波器系数被均分成了多个子滤波器，这样每一路子滤波器hk(n)的系数个数也降为1/D，可以减少滤波器计算带来的累积误差，提高精确度[2]。

4 抽取多相滤波的FPGA 实现及仿真

由图5（b）可知，采样率为fs的高速数据流通过多级延时单元Z-1后进入各路子滤波器，滤波器H0(Z)的延时为0，子滤波器H1(Z)的延时为Z-1，子滤波器H2(Z)的延时为2×Z-1，延时单元依次增加，子滤波器HD-1(Z)的延时为(D-1)Z-1。经过时延后的高速数据流在经过D倍数据抽取后再输入各自的子滤波器，输入速率为fs/D，此时滤波器的运算速率要求已明显降低。下面以子滤波器组数量为3 的多相滤波结构为例，介绍其数据处理过程，如图6 所示。整个数据处理是一个串并转换的过程，高速数据流x(n)速率为fs，每3 个样点一组进行串并转换，在子滤波器进行处理之前要进行3 倍数据抽取，然后并行送入子滤波器组中实现并行计算，每个子滤波器数据输入速率为fs/3，实现了滤波器运算降速处理。

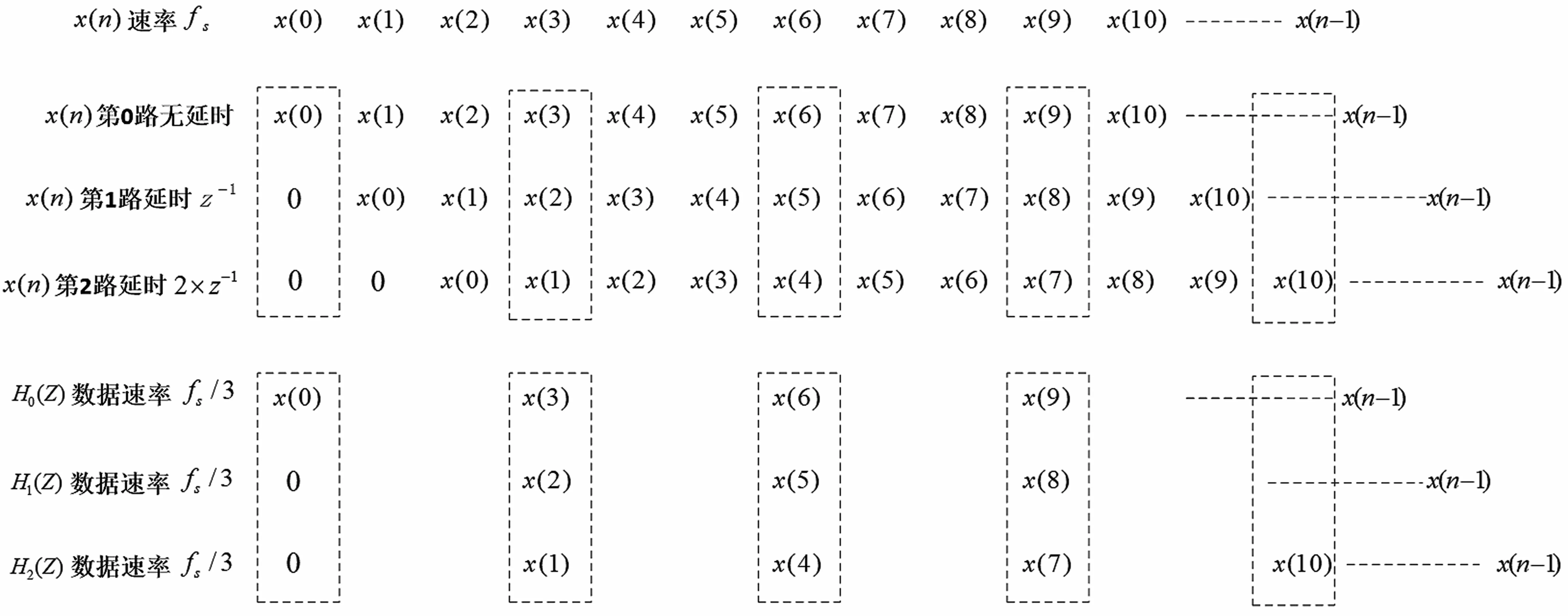
图6 抽取器的多相滤波结构数据处理过程

根据抽取后采样数据在子滤波器输入端的分布规律，即输入的数据先送往子滤波器H2(Z)，依次递减至H0(Z)完成一次周期数据输入。下面给出抽取器的多相滤波物理实现结构，如图7 所示。

图7 为抽取多相滤波的物理实现结构，原始N阶数字低通滤波器的系数为a0,a0,…,aN-1通过系数重组，分成D组子滤波器h0(n),h1(n),…,hD-1(n)。各组子滤波器对应的系数组成如下：

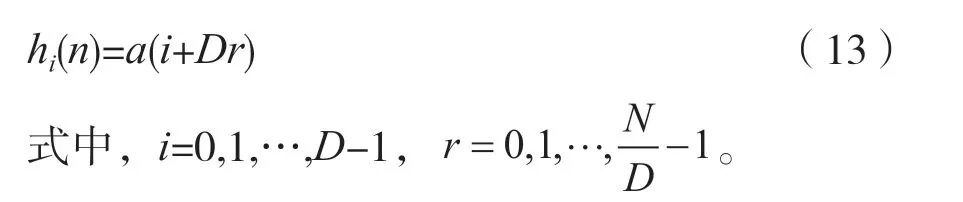
输入信号x(n)采样率为fs，通过一个选择开关分时送到不同的子滤波器输入端。每次从hD-1(n)开始输入，按采样率间隔依次递减直到输入子滤波器h0(n)完成一次周期输入，然后重复下一个周期。当完成一个周期的计算，所有子滤波器各输出一个数值，将所有子滤波器输出的数值相加作为抽取多相结构的一次输出值。抽取多相结构输出速率fs´=fs/D，fs为抽取多相滤波结构数据x(n)的输入速率。所以，相对于fs抽取多相结构的每个子滤波器工作在低速率fs/D，D个子滤波器的输出值求和后得到抽取多相滤波的输出值，实现了输出降速处理。

本文提出的接收机结构已成功应用到30～108 MHz 射频直采某设备，由于采样的频段较宽，ADC 需要提供较高的采样率才能完成对整个频段的信号取样，根据低通采样定理要求ADC 的采样率选择 250 MHz，高速采样数据流经过该接收机结构后可以大大降低滤波器数据运算要求，提高数据精度和硬件运行稳定性。下面给出多相滤波结构的Modsim仿真结果。多相滤波结构降速过程Modsim 仿真结果如图8 所示，输入信号x(n)采样率fs=250 MHz，而4 路子滤波器速率fs´=62.5 MHz，因此滤波器运算处理要求降为fs/4。

图8 多相滤波结构速率变换

图9 为多相滤波和低通滤波两种结构在相同数据速率输入条件下，利用FPGA 开发软件Vivado 进行时序性能评估对比。可以看出，在同样输入条件下多相滤波的时序裕度（Slack）更优为1.784 ns，而采用低通滤波的时序裕度为0.415 ns。因此，从时序性能评估报告来看，采用多相滤波结构的接收机运行稳定性更高。

图9 低通与多相结构FPGA 时序裕度

通过以上仿真和软件评估，假定在ADC 的采样率fs=250 MHz、位宽为16、滤波器系数N=32、抽取值D=4 的条件下，可以得出多相结构和低通结构在采样速率要求、累计误差及稳定性方面的对比结果，如表1 所示。

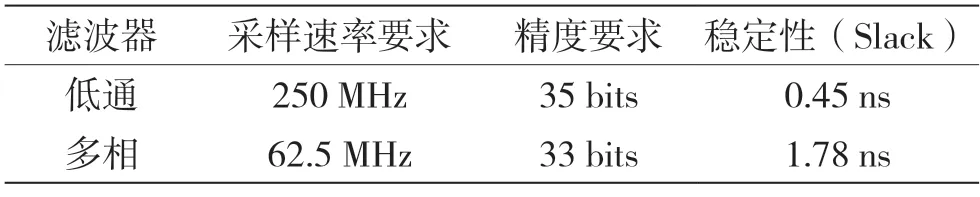
表1 低通与多相性能比较

5 结语

本文重点介绍了多相滤波技术，提出了基于多相滤波的软件无线电接收机结构，分析和论证了该结构所具备的特点。通过计算及仿真对比可知，相对于低通抽取结构，该结构计算要求降低 1/D2，同时大大降低了滤波器累积误差，提高了计算精度，在实时性要求高的场合是一种高效的解决方案。该结构已成功运用到30～108 MHz 频段射频直采某设备，采用ADI 公司的某ADC 芯片，采样速率fs=250 MHz。接收机模块采用Xilinx 公司的 Zynq-7000 系列FPGA 实现。