多参数影响下输电线链式脱冰实验研究

李孟珠，晏致涛，熊 辉，游 溢,2

( 1.重庆大学 土木工程学院,重庆 400045; 2.国网新疆电力公司 电力科学研究院,乌鲁木齐 830011)

输电线路脱冰振动是造成电力系统损害的自然灾害之一。在一定的温度和风条件下，输电线路上的覆冰会脱落，从而引起导线上下振动和横向摆动，极易造成线路闪络、跳闸事故的发生，甚至输电线路的倒塌，威胁整个供电系统的安全。2008年，华中、华东地区3次大范围的雨雪冰冻天气，使输电线路覆冰极为严重，南方很多地区的输电线路发生多起覆冰事故，导致电力中断、交通瘫痪等后果，直接经济损失达1 100多亿元[1]。因此，研究覆冰输电线脱冰后的振动响应对导线间距和输电线路的安全运行具有重要的工程实用价值[2-4]。

目前，关于覆冰输电线的脱冰[5]跳跃研究主要采用数值仿真[6-8]和物理试验等两种手段。有关数值仿真的文献很多，不论是基于有限元的建模、瞬态脱冰的响应计算分析，还是对于参数的影响及分析都已经进行了比较系统和深入的研究,本文不再赘述。有关物理模拟试验方面[9]，起初是将均匀冰重转换成集中质量悬挂在跨中的方法模拟实现输电线路覆冰进行的脱冰实验，从而测得各档架空线的脱冰跳跃高度[10]。Jamaleddine等[11]依据人工建立的气候室尺寸，设计出仅为3.22 m档距的两档架空线缩尺模型，对覆冰后架空线的多种真实脱冰工况进行物理模拟，瞬时状态记录了架空线路的最大跳跃高度以及各挂点的张力变化。在冰冻实验室，Kollár等[12]完成了单档输电线的湿雪脱落试验，并模拟了在多种自然条件下输电线的湿雪脱落。国内夏正春[13]通过悬挂集中荷载重物实现输电线覆冰的模拟，开展了单档导线的整跨脱冰模拟试验，测量了跨中导线的张力。王璋奇等[14]采用人工覆冰和集中质量两种方法来模拟单档覆冰输电线的脱冰振动实验，同时对比了两种模拟覆冰方法对脱冰跳跃动力响应带来的影响。除了对输电导线的脱冰跳跃观测，刘春城等[15]研究了五塔四档塔线体系模型在覆冰条件下的脱冰冲击对输电杆塔的最不利工况以及位置。黄新波等[16]对档距组合的输电线路做了研究，得到了输电塔线体系的动张力和幅值特性以及多参数对脱冰的影响规律。王璋奇等[17]也研究了输电线路同时脱冰下的动张力特性。

上述文献在脱冰模拟试验方面都有各自的研究重点，大多试验只关注了瞬时脱冰。而实际自然界中，蒋兴良等[18]在自然覆冰实验站开展的直流融冰实验记录和观测均表明输电线路的脱冰是一个链式过程。在现有的试验中很少有对高差的研究，但实际中，有很多输电塔线是建立在高山中的[19]，需要考虑实际工况中的高差影响，所以现有的试验模拟是有不全面之处的。文章在前期试验的基础上进行改进，试验通过集中荷载代替覆冰荷载方法，利用PCL电路图来控制不同电磁铁的磁性以实现覆冰荷载脱落的模拟。有效地完成了模拟现实中各种复杂的脱冰工况的过程。综合考虑了高差、防震装置、模型的动力相似、脱冰方式、脱冰工况的多样性，使用精度达到纳米级别的高速摄像仪DIC-3D准确测量脱冰跳跃过程中位移的变化来反映单跨输电线路脱冰振动响应。

1 试验模型设计

1.1 模型设计

本试验模拟孤立档下的单导线脱冰，考虑原型输电线的动力特性以及试验长度的限制，取试验模型的几何相似比为

cl=lm/lp=1/30，

(1)

式中：lm和lp分别为模型和原型的长度；cl表示试验模型与原型的长度相似比。这里取模型缩尺比为1∶30，原型档距为270 m，模型单跨档距9 m。

为了保证构件的拉伸刚度，使用抗侧弯能力低的碳素线作为模拟导线的材料。通过输电导线大小的计算，选择碳素线的型号为10号，直径为0.6 mm。

在结构动力试验中，为了保证几何相似的基础上动力相似，根据Froude和Cauchy数相似，Frm=Frp和Cam=Cap,其中Frm,Cam为模型的Froude和Cauchy数，Frp,Cap为原型的Froude和Cauchy数，即可以推导出以下密度的相似比条件为

Cρ=CE/CgCl，

(2)

式中：Cρ为密度相似比；CE为弹模相似比为1；Cg为重力加速度相似比；Cl为长度相似比。

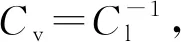
考虑到在试验中，模型重力加速度应和原型重力加速度相同，取重力加速度的相似比Cg=1。采用人工配重的方法解决密度相似比的问题，导线原型质量mρ=7.668 kg，模型导线单位长度配重质量∇m=8.53 g。因为试验中要用到电磁铁吸盘，将电磁铁吸盘均匀分布在输电线上，而此时的电磁铁吸盘质量刚好满足了输电线的配重质量。

按照比例1∶30设计的导线与原型参数如表1所示。

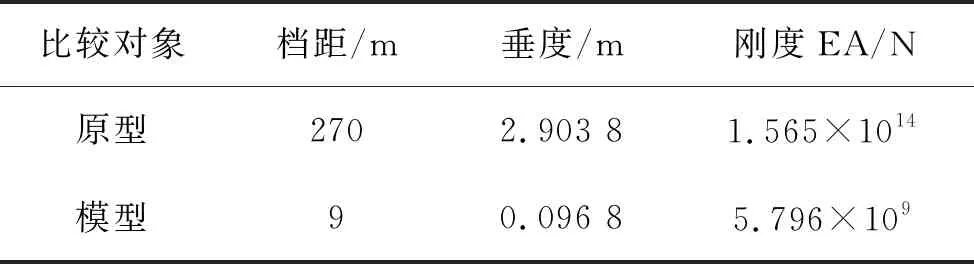
表1 导线原型与模型参数

1.2 导线及覆冰模拟

输电线路单位长度上的覆冰质量用M表示，单位为kg/m；覆冰密度为900 kg/m3；导线直径为d，覆冰后为D，单位为mm。导线覆冰质量为

M=ρ(D2-d2)×10-6×π/4，

(3)

式中，ρ为覆冰密度。

研究证明，采用集中荷载时导线跳跃的位移和张力变化曲线与均匀荷载时的变化基本吻合[16,19]，本文采用集中荷载重物进行实验，通过PCL电路图控制电磁铁的磁性来模拟覆冰输电导线的脱冰过程。自重单个集中荷载的质量由公式M=mL/n来确定，式中：m为单位长度上导线覆冰的质量；L为每跨导线的长度；n为悬挂重物数，取n=12。导线及覆冰模拟如图1所示。

图1 输电线覆冰模拟及脱冰示意图

通过PCL电路图控制集中质量脱落的方法模拟导线脱冰的顺序，电路图布置图如图2所示。

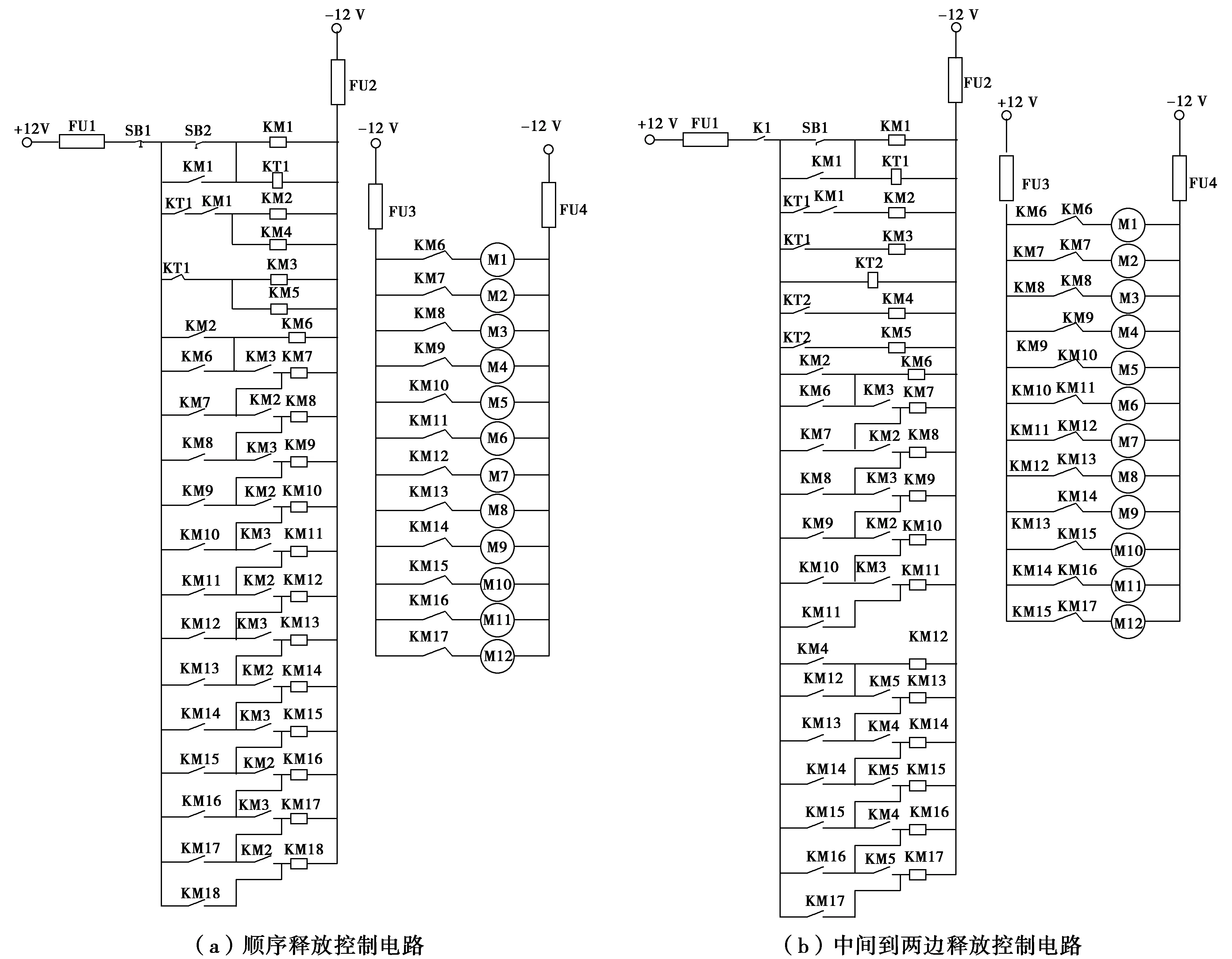
注： FU代表熔断器，SB代表控制按钮，KM代表接触器，KT代表时间继电器，M代表电磁铁。KM2,KM3,KM4,KM5是具有四对触点的接触器，其余的接触器为具有两对触点的接触器

在图2(a)中，右侧电路是按从左到右的顺序控制电磁铁磁性的释放一次回路图，即是顺序控制释放电路的执行电路图；左侧电路是顺序控制电磁铁磁性释放的二次回路，即是顺序控制释放电路的控制电路图。顺序控制电路磁性释放的运行步骤如下：

1)首先设置好时间继电器KT1的预置时间t1；

2)按下控制按钮SB2，此时KM1被接通同时自锁现象发生，之后KM2和KM6也瞬时接通，此时KM6的常闭触点被打开，M1失电磁性消失，该段是模拟覆冰的集中荷载重物脱落；

3)KM1接通时，KT1就开始计时，到达预置时间t1后，KT1的延时触点动作发生使得KM2失电断开和KM3得电接通，进而KM7得电被接通，KM7的常闭触点动作打开使得M2失电磁性消失，此段的模拟覆冰重物脱落；

4)预置时间KT1动作完成后，常断触点KT1闭合，同时接通KT1的复位开关，KT1重新计时开始；

5)t1预置时间达到后，KM2重新得电， KM8接通，KM8的常闭触点断开使得M3失电磁性消失，覆冰集中荷载脱落;

6)如此往复，根据t1的预置时间，KM6至KM17的常闭触点依次断开，达到覆冰顺序释放的目的。

在图2(b)中，右侧电路为从中间到两边的控制电磁铁磁性的释放一次回路图，即从中间到两边控制释放电路的执行电路图；左侧电路为从中间到两边的控制电磁铁磁性的释放二次回路图，即从中间到两边控制释放电路的控制电路图。

从中间到两边控制释放电路的运行步骤如下：

1)首先设置好时间继电器KT1和KT2的预置时间t1和t2;

2)按下控制按钮SB1，此刻KM1被接通同时自锁现象发生，KM2，KM4，KM11,KM12也瞬时接通，KM11和KM12的常闭触点被打开，M6和M7由此失电磁性消失，中间两个覆冰集中荷载脱落；

3)KM1接通时，KT1和KT2就开始计时，t1和t2的预置时间达到后，KT1和KT2延时触点动作KM2和KM4失电断开，KM3和KM5瞬时得电接通，使KM10和KM13得电接通，KM10和KM13的常闭触点打开使M5和M8失电磁性消失，模拟覆冰集中荷载重物脱落；

4)KT1和KT2计时完成后，KT1和KT2常断触点闭合，并接通KT1和KT2复位开关，KT1和KT2重新计时开始；

5)t1和t2的预置时间达到后，KM2和KM4再次得电，此时KM9和KM14被接通，KM9和KM14的常闭触点断开使得M4和M9失电磁性消失，集中荷载脱落;

6)如此往复，根据t1和t2的预置时间，KM6至KM11和KM12至KM17的常闭触点依次断开，达到覆冰中间到两边释放的目的。

1.3 测量设备

跳跃位移采用高速摄像仪DIC-3D进行采集，它是一个可以通过非接触方式进行光学三维变型测量，主要用于分析、计算和记录变形，DIC-3D系统提供的包括数据、图表和云图等测量结果，能够直观清晰地反应被测物体的变形行为，为用户提供方便，测量精度达到了纳米级别，所以，测量设备采用DIC-3D提高了试验的精度。

2 试验过程

脱冰试验工况见表2所示。通过固定质量，来模拟一定长度单元上覆冰输电导线上的冰荷载重量，实验采用导线上均匀分布12个集中荷载进行，通过改变导线的脱冰速度、脱冰方向、高差的变化以及防震锤的有无，模拟不同工况下的导线脱冰。通过电磁铁释放器控制不同指定位置悬挂的重物脱落的脱冰顺序，并利用高速摄像仪来记录导线脱冰的跳跃位移。

表2 脱冰试验工况表

研究了不同倾斜角高差下对脱冰振动的影响，设定倾斜角0°，5°，15°，30°，45°，60°和75°下脱冰跳跃的高度。为在山区大高差的输电线路设计提供了理论支持及有价值的实用意义。

3 试验分析

3.1 脱冰速度的影响

等高差下分别设定时间继电器为1 s，2 s和4 s，对应脱冰速度分别为7.5 m/s链式脱冰、3.75 m/s链式脱冰和1.875 m/s链式脱冰，脱冰方向全都设置为从中间到两边脱冰。并与瞬时脱冰进行对比，得到不同脱冰速度下的脱冰位移响应，如图3所示。不同脱冰速度相对与瞬时脱冰下脱冰跳跃的最大高度降低百分比，如图4所示。

图3可以看出，不同脱冰速度下，脱冰响应曲线不同，随着速度的降低，脱冰跳跃的最大位移幅值在降低，脱冰响应曲线的频率有所下降，瞬时也可以了解到在脱冰完全之前，脱冰速度越大，脱冰跳跃最大幅值降低越多。另外，在脱冰完全稳定之后，在所有脱冰速度工况下，脱冰响应的内力和位移均稳定于同一状态。

图3 脱冰速度不同的响应时程曲线

从图4中可以看出，瞬时脱冰为最不利情况，脱冰跳跃高度最高，随着脱冰速度的降低，脱冰跳跃最大高度也在降低，但是降低到一定速度之后脱冰跳跃最大高度基本上不变，此时脱冰跳跃高度跟同期脱冰跳跃高度相比降低50%左右。实际工程中脱冰并不是瞬时脱冰的，而是一定速度的链式脱冰，所以此次试验也更加接近于实际工况，设计中采用瞬时脱冰是偏于保守的。

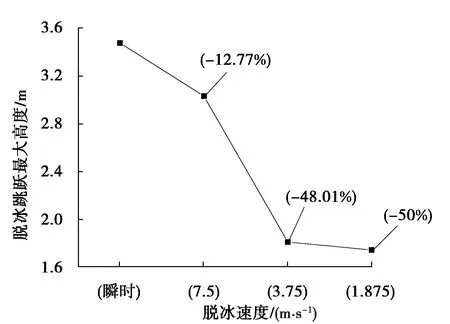
图4 脱冰速度不同的最大跳跃高度降低比

3.2 防振锤效果

从图5可知，加入防振锤后，脱冰跳跃最大位移降低幅值有所增大，频率降低，同种工况下，防振锤能够有效降低脱冰跳跃的最大高度，瞬时脱冰最大跳跃位移降低了20%，而链式脱冰最大跳跃高度降低了35.88%。所以在链式脱冰中防振锤的效果更加明显。而实际工程中也是一个链式脱冰的过程，防振锤可以很好地起到一个减振的效果，这为设计院中对于输电线路的减振设计提供理论支撑。

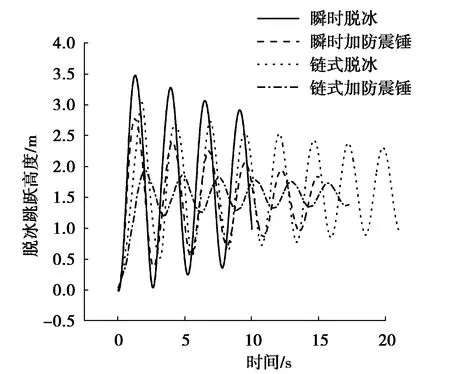
图5 考虑防振措施的脱冰时程曲线

3.3 不同倾角高差对脱冰振动的影响

研究不同倾角高差对于线路脱冰振动的影响。设计了高差倾角为0°，15°，45°和75° 4种链式脱冰下的工况。保证各种工况下跨中的张力保持一致。脱冰方向从中间到两边，链式脱冰速度为7.5 m/s为不变量，得到不同倾角高差下输电线路跨中脱冰响应如图6所示。

从图6可知，在不同倾角高差下，随着高差倾角的增大，脱冰跳跃的最大跳跃位移一直在增大，脱冰振动的时程曲线频率在一直降低。不同倾角高差下脱冰跳跃的最大高度进行分析如图7。图7表明，得到脱冰跳跃最大高度随着不同倾角高差的增大而非线性增加，当倾斜角度达到75°时，脱冰跳跃最大高度比没有高差时增大了64.16%。这就给实际工况中设计不同高差输电线路提供了理论支撑，特别是在山地上建立的大跨度大高差的输电线路，要充分考虑这个因素，做好防振减振措施，避免不必要的事故发生。

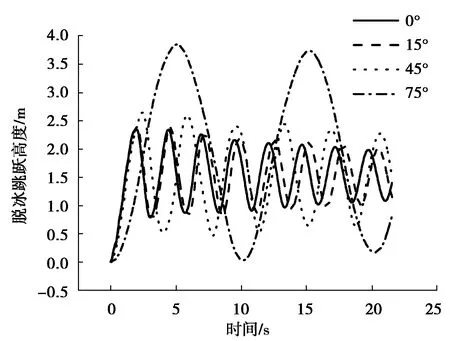
图6 倾角高差不同的响应时程曲线

图7 不同倾角高差下的脱冰跳跃最大高度

3.4 脱冰方向对脱冰振动的影响

在线路有高差环境下，线路的脱冰方向对振动响应也有较大影响。这里研究不同脱冰方向对于脱冰振动的响应分析，典型高差为5°，设计了从中间到两边链式脱冰，从低到高的链式脱冰和从高到低的链式脱冰3种工况进行脱冰方向的研究，脱冰速度取为7.5 m/s，测试得到不同脱冰方向的时间响应时程曲线(图8)。

图8 脱冰方向不同的响应时程曲线

从图8可以看出，在有高差的工况中，脱冰跳跃的最大高度与脱冰方式或者方向有着密切的关系，其中从中间到两边的脱冰方式是最不利的情况，脱冰跳跃最大位移最大，频率最大，而从较低端到较高端脱冰比从较高端到较低端的脱冰跳跃最大位移略高1.3%，所以它们的位移响应几乎相同，频率几乎一样，但它们比从中间到两端脱冰方式的脱冰跳跃最大高度降低了40%。

4 结 论

在已有脱冰实验的基础上对输电线路脱冰振动进行改进试验研究，综合考虑了在链式脱冰和瞬时脱冰下的高差、防振措施、脱冰速度、脱冰率、覆冰厚度、脱冰方向等因素的工况研究，通过使用精度达到纳米级别的高速摄像仪得到的脱冰振动响应时程曲线和分析对比后总结出如下的结论：

1)瞬时脱冰在不同脱冰速度为最不利情况，随着脱冰速度的降低，脱冰跳跃最大高度降低，脱冰跳跃最大高度与瞬时脱冰跳跃高度相比最终趋于降低50%左右。

2)在有减振装置如防振锤情况下，链式脱冰的减振效果更加明显。

3)脱冰跳跃最大高度随着不同倾斜角高差的增大在非线性增加，脱冰振动需要充分考虑高差的影响。

4)从中间到两边脱冰方式为最不利情况，实验案例表明，它们比从一端到另一端的脱冰方式的脱冰跳跃最大高度增大了40%。